Графовое моделирование процессов импульсных систем с запаздыванием

DOI:

Рассмотрим вначале моделирование процессов на базе динамических графов для одномерных систем [1; 3–10], в которых объект управления представлен в виде динамического звена l -го порядка с запаздыванием (см. рис. 1, а ). В зависимости от величины запаздывания могут представиться следующие случаи:

1) 6 = mT + т, 2) 0 = mT, 3) 6 = т, где T – период повторения импульсного элемента, т - запаздывание, m - целое, 0 < т < T.

При построении графовой модели будем исходить из общего случая, когда запаздывание равно 6 = mT + т- С учетом величины запаздывания выделим подграфы обратной связи Gt = (X', X", V), tос где

X' = { x 1 ( m + 1 T )},

X" = {х1[2( m+1T)],..., x, [2(m+1T)]} v v {x1[2(m + 1T) + т],...,X;[2(m + 1T) + т]},

Vv e V[◊ = Cj(T) v Cj(T -т)], подграфы процесса Gt = (X', X", V), пр где

X' = {x1 (m +17),..., xl (m + 1T)}, X" = {x1( m + 1T + т ),..., xl (m + 1T + т)} v v {x1( m + 2T),..., xl (m + 2T)}, Vv e V[◊ = ац(T) v ay(T -т)], подграфы входного воздействия Gtx = (X", X", V), где

X ' = { f (0)},

X" = {x1( m + 1T),..., xl (m + 1T)} v v {x1(m + 1T + т),...,xl(m + 1T + т)},

V v e V [ ◊ = b_y(T - т ) v b_y(T )].

В выделенных подграфах (рис. 1, б–г ) можно увидеть особенности формирования их структуры и передач. Для получения графа

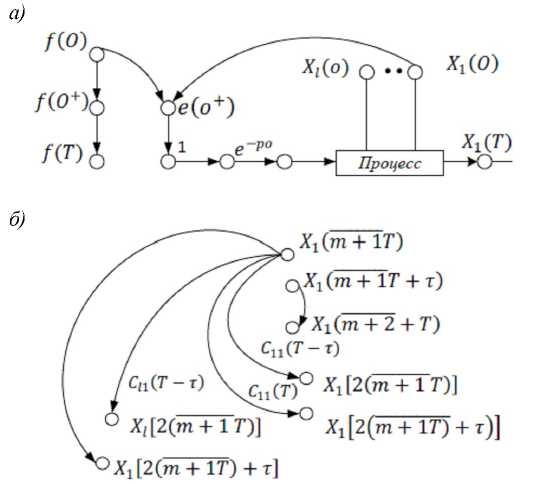
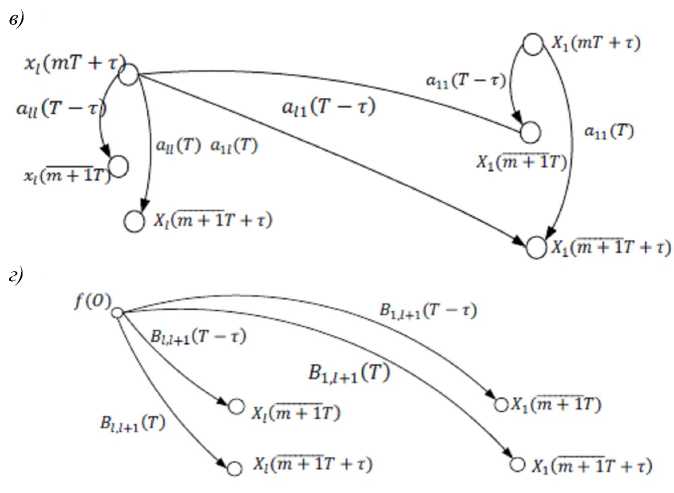
Рис. 1. Макроструктура импульсной системы с запаздыванием ( а ), подграфы динамических графов импульсной системы с запаздыванием ( б, в, г )

системы (рис. 1, а ) достаточно взять объединение подграфов, то есть

Gt = Gt Y Gt Y Gt (1) вх пр ос.

Так, на рисунке 2 показаны графовые модели для систем с различными значениями запаздываний при l = 2.

Из анализа структуры графовых моделей выводятся эффективные в вычислительном отношении уравнения динамических процессов импульсных систем с запаздыванием.

Например, для системы с запаздыванием 0 = _т (рис. 2, а ) уравнения процессов имеют вид

Д nT ) = A ( T - т ) ^р ( n - 1 T + т ) +

+ B( T - т ) f ( n - T ) + C( T - т ) x 1 ( n - T ) , ⁽²⁾

^p ( nT + т ) = A ( T ) X ( n - 1 T + т ) +

+ B ( T ) f ( n - 1 T ) + (^P( T ) x 1 ( n - 1 T ).    ⁽³⁾

Аналогично для системы с запаздыванием (см. рис. 3) уравнения динамических

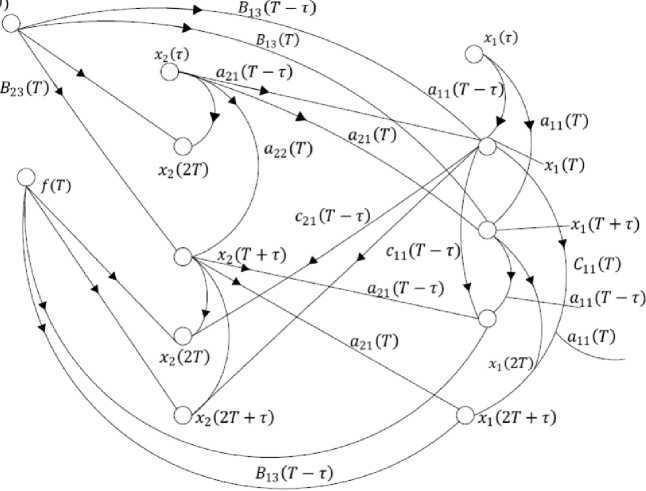
Bi3(D

б)

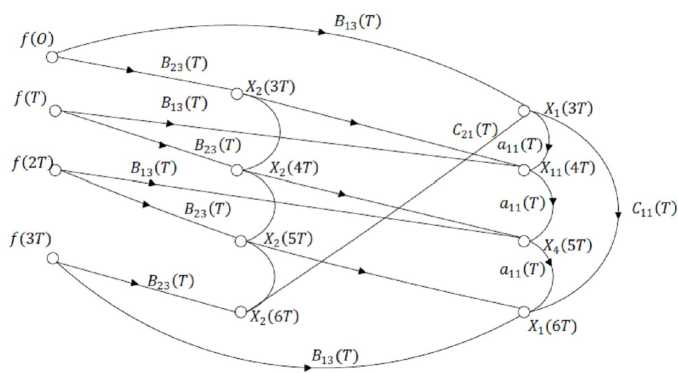
Рис. 2. Граф импульсной системы с запаздыванием 0 = т , l = 2 ( а ), граф импульсной системы с запаздыванием 0 = mT , l = 2, m = 2 ( б)

процессов получены непосредственно из графовой модели и имеют вид

^p ( nT ) = A(T - т ) ^p ( n - 1 T + т ) +

+ B ( T - т ) f ( n - 0 T ) + C(T - т ) . ( n - 0 T ) ,⁽⁴⁾

^p ( nT + т ) = A (T ) ^p ( n - 1 T + т ) + + B ( T ) f ( n - 0*T ) + C(T ) x 1 ( n - 0*T ),

где 0*( m + 1)T = m +1,

p(0) = p(T) =... = .^(0) = 0.

Для последнего случая равнение процессов принимает вид

.(nT ) = A (T ) j^p( n - 1 T ) +

+ B(T ) f ( n - 0*T ) + C(T ) x 1 ( n - 0T )  ⁽8)

Матрицы A, B, С в уравнениях (2–8) имеют размерности l x l, l x 1, l x 1, где l - порядок дифференциального уравнения непрерыв- ной части системы. Смысл элементов этих матриц ясен из рисунка 1, б–г.

Моделирование многомерных импульсных систем с запаздыванием

В многомерной системе модель каждого сепаратного или перекрестного канала представляет собой граф одномерной импульсной системы наподобие графов, изображенных, например, на рисунке 2. Для определенности порядка моделирования поясним на примере двумерной дискретной системы с запаздыванием (см. рис. 4, а ).

Для компактности изображения в многомерных системах целесообразно использовать граф-векторы каналов передач с учетом их взаимных связей, определяемых через сигналы ошибок. Дуги графа-вектора в отличие от развернутых графов взвешены матрицами, а к каждой вершине (за исключением вершин, соответствующих ошибкам) ставится в соответствии вектор-столбец переменных состо-

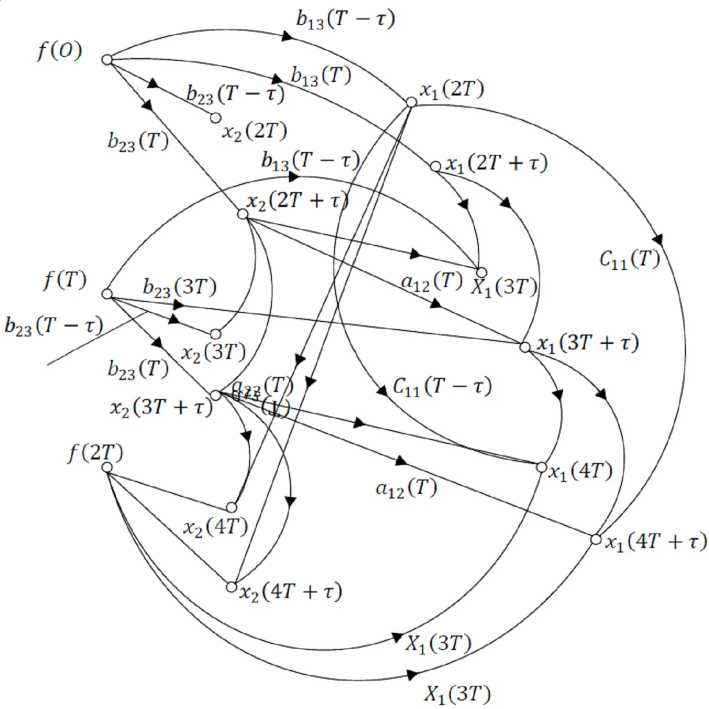
Рис. 3. Граф импульсной системы с запаздыванием 0 = mT + т , m = 1, l = 2

яний. С учетом этих замечаний графовая модель рассматриваемой двумерной системы будет состоять из двух векторных компонентов связности, представленных на рисунке 2, б . Для случая 9 = T + т , 9 ₁ = 9 2 = 9 , режим работы импульсных элементов – синхронно-синфазный.

Из рисунка 4, б можно получить выражения для расчета процессов

#( nT ) = A^X(T - т ) X A n - 1 T + т ) +

+ I^х (T - т ) e * ( n - 9 T )

Х²( nT + т ) = J1¹² ( T ) X ¹² ( n - 1 T + т ) + + B^U(T ) e ²( n - 9*T )

X²(nT ) = A²( T - т ) X²(n - 1T + т ) + + B ? ²( T - т ) e ²( n - 9 T )       ,

X²( nT + т ) = A² ( T ) X² ( n - iT + т ) + + B ? ² ( T ) e ²( n - 9*T )

X c ²¹ ( nT ) = A ²¹ ( T - т ) X²¹ ( n - 1T + т ) +

+ B ? ²¹( T - т ) e ’( n - 9 T )        ^,(15)

^р1( nT + т ) = A’( T ) ^р1( n - 1 T + т ) + + ^( T ) e ’( n - 9*T )       ’

Р( nT ) = A ¹²( T - т ) Р( n - 1 T + т ) +

+ B ¹²( T - т ) e ²( n - 9T )      , ⁽¹¹⁾

( nT + т ) = A t ²¹ ( T ) X ²¹ ( n - 1 T + т ) +

+ J ? ²¹ ( T ) e ’( n - 9T )         . ⁽¹⁶⁾

Выходные координаты системы xr ^{( rk} ) , x 2^{( rk} ) ( r , k = 1,2) определяются на основе (9–16) следующим образом:

а)

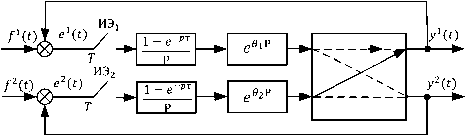
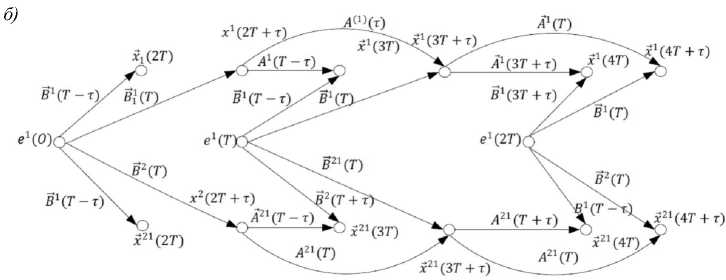
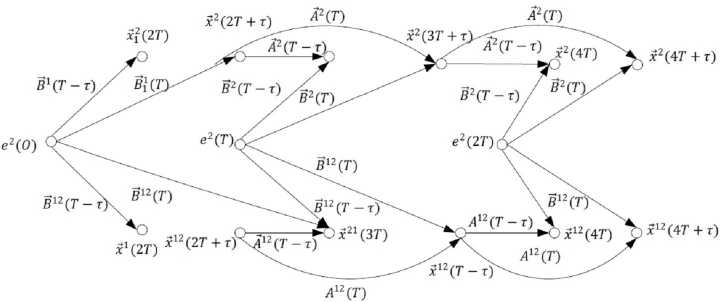
Рис. 4. Двумерная дискретная система с запаздыванием ( а ), графовая модель процессов ( б )

y 1 ( nT ) = x 1 ( nT ) + x 12 ( nT ),      (17)

y 1 ( nT + т ) = x 1 ( nT + т ) + x 1 ²( nT + т ), (18)

y ²( nT ) = x j² ( nT ) + x 1²¹ ( nT ),     (19)

y ² ( nT + т ) = x 1² ( nT + т ) + x 1²¹ ( nT + т ), x 1 ( nT ) e X ¹ ( nT ), x 1² ( nT ) e X 1² ( nT ), (20) x 1² ( nT ) e X 2 ( nT ), x 1²¹ ( nT ) e X 21 ( nT ).

y^r ( nT + т ) = xr ( nT + т ) + '^xrk ( nT + т ), k = 1( k ^ r )

x ( nT ) e x^r ( nT ), x rk ( nT ) e x^rk ( nT ).

Второй случай: 6 = mT , m = 1,2,...

Для моментов i=1, 2,…, m

X^r ( iT ) = Ji ^r (T ) X^r ( i - 1 T ),        ⁽³¹⁾

X^rk ( iT ) = Ji ^rk (T ) X^rk ( i - 1 T ),      (32)

для моментов n=i >m

Для общего случая N -мерной системы примем переменную состояния x [ ^{( rk} ) ( r , k = 1,2,..., N ) за выходную величину соответствующего сепаратного ( r ) или перекрестного ( rk ) канала. Рекуррентные соотношения для расчета процессов N -мерной синхронно-синфазной системы с ненулевыми начальными условиями получены в следующем виде:

Первый случай:

6 = mT + т , m = 1,2,...; 0 <  т <  T .

X^r ( n T ) = J^r ( T ) X^r ( n - 1 T ) + J i ^r ( T ) e^r ( n - 6 t ), (33)

P ^rk ( nT ) = J^rk (T ) X^rk ( n - 1 T ) +

+ J i ^rk (T ) e^r ( n - 6*T ).            ⁽³⁴⁾

Выходные переменные y^r ( nT ), y^r ( nT + т ) определяются согласно (29), (30).

Для моментов iT , iT + т, i = 0,1,...

Xr (iT) = Jir (T) Xr (i-1T ),

Pr (iT + т) = J (т) Pr (iT ),(22)

xrk (iT) = Jrk (T ) Prk (i-1 T ),

Xrk (iT + т) = Jrk (т) Xrk (iT).

Для моментов n = i >m

Xr (nT) = J r ( t - т) Xr (n-1T+т) + P          -----r

+ B^r (T - т ) e^r ( n - 6 T ),

X^r ( nT + т ) = J r ( t ) X^r ( n - T + т ) +

+ Jr (T)er (n - 6T),

X^rk ( nT ) = Ji ^rk ( T - т ) ^{p rk} ( n - T + т ) +

+ J?rk (T - т) er (n - 6T),

Третий случай: 6 = т , 0 <  т <  T .

Для момента т

X^r (т ) = Ji ^r (т ) X^r (0),

Xrk (т) = Jirk (т) Xrk (0), для моментов n = 1, 2,…

X^r ( nT ) = Ji ^r ( T - т ) X^r ( n - 1 T + т ) + + J ? ^r ( T - т ) e^r ( n - 1 T ),

pr (nT + т) = Jir (T)pr (n - 1T + т) + + Jir (T) er (n-1T), prk (nT) = Jirk (T - т) Prk (n-1T + т) + + Jirk (T - т) er (n-1T),

J? ^rk ( nT + т ) = J i ^rk (T ) ^{p rk} ( n - 1 T + т ) + + J i ^rk ( T ) e^r ( n - 1 T ).

^{p rk} ( nT + т ) = Ji ^rk (T ) X^rk ( n - 1 T + т ) +

+ J^rk(T ) e^r ( n - 6*T ),             ⁽²⁸⁾

y r ( nT ) = x ; ( nT ) + f x k ( nT ),       (29)

k = 1( k # r )

На иллюстративном примере одномерной системы дадим сравнительный анализ использования для расчета динамических процессов предложенного метода и традиционного метода, основанного на использовании модифицированного z -преобразования [2].

Пример

Рассмотрим одномерную систему с чистым запаздыванием, изображенную на рисунке 5. Входное воздействие f ( t )=1( t ), период повторения импульсного элемента T = 1 сек , запазды-

вание 9 = T + т = 1 + 0,25. Объект описывается передаточной функцией W ( p ) = V( Р + 1), T = 1. Требуется рассчитать выходной процесс x ( t ).

Расчет переходного процесса методом модифицированного z-преобразования

W *( z , m ) = z W * ( z , m ) = z ¹ Z_m

1 - e - Tp

Р ⁽ Р ⁺ 1)

Из таблиц определяем W ₁ ^* ( z , m ):

W4 z , m ) = z . ' z

f 1           — m \

1 e । v z—1 z - 0,368 J (42)

Соответствующее z -преобразование записывается следующим образом:

W *⁽ z ) = w *⁽ z , m )|      = w *⁽ z , m )|      =

I m = 1 - 5                    I m = 0,75

- z - 1 f 1       0,473 "         .(43)

= z ² I z - 1 z - 0,368 J

Модифицированное z -преобразование выходной величины при ступенчатом входном сигнале дается выражением

X •( z , m ) = R •( z ) W^m =

1 + W 1* ( z )

= z f     z - 0,368 - e"^m z + e"^m    \ (44)

= z - 1 ( z ³ - 0,368 z ² + 0,527 z + 0,105 J

Сама выходная величина равна x ( n, m) T =

=      _______________ z (1 ^- e-^m ) ⁺ e-^{m -} 0,368 _______________ z-dz . (45)

2nj { ( z - 1)( z + 0,17)( z - 0,269 + j 0,74)( z - 0,269 - j 0,74)

Вычисление этого интеграла с помощью метода вычетов приводит к следующему результату:

x ( n , m ) T = 0,5 + (0,63 - 1,37 e ~ ^m )( - 0,17) n +

+ 1,35( - 0,787) n ⁺¹ (1 - e - m )cos [ ( n + 1)70 ^o + 76 ^O ] +

+ 1,52(0,787) n ( e - m - 0,368) cos( n • 70 ^o + 76 ^O ), ⁽⁴⁶⁾

t = ( n - m ₅ + m ), 0 <  m <  1, m ₅ = 1 - 5 = 0,75.

График этой функции приведен на рисунке 6.

Расчет переходного процесса графодинамическим методом

Учитывая величину запаздывания, воспользуемся соотношениями (4), (5). В итоге получим следующие значения:

x ( T ) = 0; x (1,25 T ) = 0;

x (2 T ) = (1 - e 5 ^T ) f (0) + e ~⁰'^{75 T}x (1,25 T ) = 0,53;

x (2,25 T ) = (1 - e ^{- T} ) f (0) + e ^{- T}x (1,25 T ) = 0,632;

x (3T ) = (1 - e ~⁰'^{75 T} ) f ( T ) + e "°'⁷⁵ T x (2,25 T ) = 0,829;

x (3,25T ) = (1 - e ^{- T} ) f (T ) + e ^- T x (2,25 T ) = 0,864;

x (4T ) = (1 - e ~⁰'^{75 T} ) f (2T ) + e ~⁰'^{75 T}x (3,25T ) = 0,657;

Рис. 5. Замкнутая импульсная система для иллюстрирующего примера

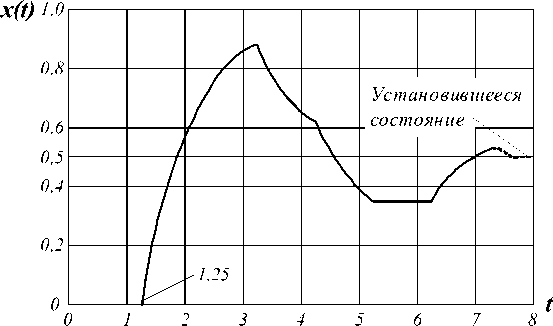
Рис. 6. Процесс на выходе системы, изображенной на рисунке 5

Значения процесса полностью совпадают с результатами, полученными методом модифицированного z -преобразования. Сравнение двух методов показывает, что даже в случае одномерных систем расчеты значительно проще выполняются на базе предложенного метода динамических графов. Применение модифицированного z -преобразования для аналитических исследований особенно проблематично в случае многомерных импульсных систем с запаздыванием, так как сопровождается трудностями принципиального характера, обусловленными структурной сложностью и проблемой формализованного математического описания процессов при использовании традиционного подхода.