Граничное условие «закон стенки» с учетом шероховатости для модели турбулентности Спаларта-Аллмараса

Шероховатая поверхность встречается в многих случаях, например, поверхность ледяного слоя при моделировании процесса, обледенения. Шероховатость может оказать большое влияние на. пограничный слой и, как следствие, на. процесс нарастания льда. Она. может увеличивать коэффициент конвективной теплопередачи из-за. двух причин: повышение коэффициента трения и возрастание площади поверхности теплоотдачи. Таким образом, при моделировании нарастания льда, необходимо учитывать этот факт. Для этого часто используются модификации модели турбулентности SST к — ш или SA [1-4], в настройке которых применяют некоторые изменения, зависящие от шероховатости. Также надо отметить, что закон стенки модифицируется по сравнению со случаем гладкой поверхности.

«Московский физико-технический институт (национальный исследовательский университет)», 2021

2.    Эффект шероховатости

Как показано на рис. 1, неровности на поверхности льда имеют разнообразную форму, и это сильно затрудняет изучение шероховатости. Для простоты широко используется «эквивалентная песочная модельная» шероховатость с одинаковой высотой бугорков k_s. На практике также используется ее безразмерное значение:

k t =

ksuT

, V

где u_T

ij't; ~ динамическая скорость, V - кинематическая вязкость.

Рис. 1. Ледяной слой па. профиле

Проведенные И. И. Никурадзе исследования движения жидкости в трубах, поверхность которых покрыта, однородной песочной шероховатостью [5], показывают, что влияние шероховатости на. течение можно разделить на. три режима:

• 1.    Гидравлическая гладкость k⁺< 5: зерна шероховатости полностью погружены в вязкий подслой и не наблюдается влияния шероховатости на. сопротивление и профиль скорости.

• 2.    Переходный режим 5 < k+ < 70: часть элементов шероховатости выступает из вязкого подслоя и начинает оказывать влияние на. характеристики течения, создавая дополнительное сопротивление.

• 3.    Полное проявление шероховатости 70 < k+: гидравлическое сопротивление полностью зависит от сопротивления элементов шероховатости, эффектом вязкости можно пренебречь.

С учетом шероховатости меняется закон стенки (рис. 2). По мере увеличения шероховатости логарифмический закон принимает вид u+ = 1 ln(y+) + С - Au+, (2) к где у' = ^^, u+ = ^, к = 0.4, С = 5.5 , величина сдвига Au+ зависит от безразмерного параметра шероховатости k+.

По данным эксперимента. И. И. Никурадзе:

Au+

= ¹ ln(k+) + С - В, к

где

В =

5.5 + t ln(k+), 1 < k⁺ < 3.5,

6.59 +1.521 ln(k+),   3.5 + < 7.0,

9.58,  7 + < 14,

11.5 - 0.7ln(k+),   14 + < 68,

8.48,  68 + .

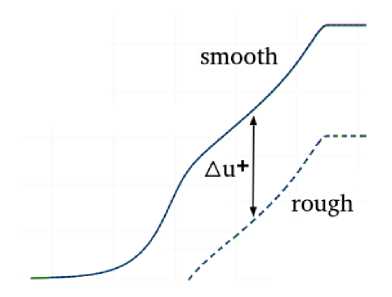
Рис. 2. Профиль скорости

Другая формула для определения сдвига является формулой Колебрука-Григсона [6,7]:

An+ = — ln Г 1 +--, к = 0.41.

к \    ехр(3.25к) /

Сравнение двух формул представлено на рис. 3. Основное отличие наблюдается в переходном режиме. В данной работе для изучения всех режимов используется формула Колебрука-Григсона.

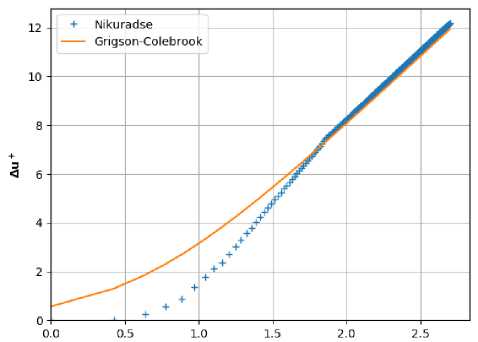
1ои< к/)

Рис. 3. Сдвиг Аи+

3.    Модификация модели Спаларта-Аллмараса для шероховатой поверхности

Стандартная модель Спаларта-Аллмараса с одним дифференциальным уравнением, составляющимся относительно переменной ), имеет следующий вид [1]:

Di

Dt

= 1([V.((i + i)Vi)] + C_b2[(W).(W)]) + СД(1 - ^Si - (cuf_w - ^ Ц (0 . (5)

Турбулентная вязкость вычисляется по формуле

№ = pif vi .

В этом уравнении:

V t = f o1 V, f o1 = уЧ^Д , У = у,

S = Q + fy2 уг , Л2 = 1 — 11 ^Хт , ^{J 0 2} K 2 t , ^{J 02}          1+xf vi ,

Для моделирования обтекания шероховатых поверхностей Б. Аупуа и П. Спаларт в работе [1] предложили использовать модификацию, в которой граничное условие на стенке V = 0 заменено условием dV _ V

дп   d1

где п - нормаль к стенке, d - росстояние, которое необходимо искусственно увеличить: d = d_min + 0.03fc_s, d_min - расстояние до стенки.

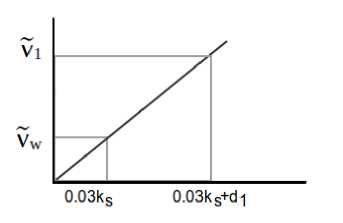
Рис. 4. Граничное условие

Такое условие представлено на рис. 4. Его приближенная формула имеет следующий вид:

Д — Vw _ Vi    _ Vw di = di + 0.03fcs = 0.03ks , где Vi - параметр в центре пристенной ячейки.

Кроме того, изменяются следующие функции:

У = У + C R1 t ,C_R 1 =0.5, у ^fo2 = 1 ^— П#Т.

4.    Граничное условие «закон стенки»

Главная идея Б. Аупуа и П. Спаларта [1-3] заключается в том, чтобы искусственно увеличить турбулентную вязкость ^t на стенке для моделирования эффекта шероховатости. Метод основан на следующем принципе. Используется некоторый сдвиг уд, такой, чтобы градиенты скорости на шероховатой и гладкой поверхностях удовлетворяли соотношению dn+ _ du+ Эу+ у+ ду+

.                                                  (9)

У ⁺⁺ У о

’) — ^ + ( у + ) .                               (10)

Интегрируя это соотношение, получаем

^+(У+) = ^+(У+ + Уо

И тогда сдвиг Ап+ определяется как

А^+ = и+(у+).

(И)

Для определения у+ можно использовать профиль скорости Рейхардта для гладкой пластины:

и ⁺

- ln(1 + ку ⁺ ) + 7.8 к

1 ¹ — ^exp⁽ -у-) — 11 ехр^{( -} 0.33у ^{+ )}

Из этого соотношения можно задать Аи+ и вычислить у+:

у + = max(0, 3.251п(к°'⁹) — 5.5) exp

(-к+) 880

+ 0.0318к+, по данным II.11. Никурадзе,

у + = (0.202к+ + 10.1) th

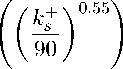
по данным С. Кодебрука.

Их сравнение представлено на рис. 5. В данной работе используется формула (14).

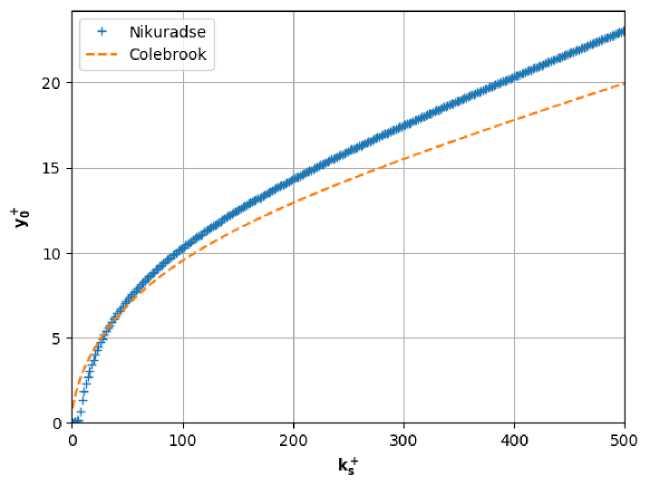
Рис. 5. Сдвиг у+

Алгоритм граничного условия «закон стенки» устроен следующим образом.

На первом этапе, в центре приграничной ячейки, на расстоянии уі = di определяется тангенциальная составляющая скорости иі. Далее необходимо задать температуру стенки Tw, метод определения которой описан в работе Власенко [12]. Зная Tw, можно вычислить вязкость ц№ и плотность газа pw на стенке. При этом предполагается, что давление на стенке равно давлению в центре приграничной ячейки pw = pi. Далее методом деления отрезка пополам решается уравнение (10), чтобы найти подходящее значение у+. На каждой итерации г 'задано у+ = ^(у+п.і + у+хД тогда у + Д№ , ksUTpW       и1

u_T =-----, к + =-------, u + = .

^p w ^y1         ^p W          ^U T

Значение сдвига y + вычисляется по формуле (14), по данным С. Колебрука, и⁺ (у⁺ + у+), и+ (у⁺) - по профилям X. Рейхардта (12). Затем вычисляется невязка, уравнение (10):

R = ^и + - ^и+⁽у ^{+ +} у ^{+ ) + и} + ⁽у ^{+ )}.

По ее величине определяется новое значение у^л^! ил и у + _ах г+і- Наконец, зная решение у⁺ . найдем

у*2^

Tw — о у2Рщ и диффузионные потоки на стенке.

Также можно использовать профиль скорости с тепловым потоком [12]:

у+ = |

и⁺ + е^-кЛ ^Е(и⁺) - 1 е^-кЛ Е (и⁺), 10 <  у⁺,

-

ки⁺ — 2 (ки⁺ )²

-

6 (ки+)3

- та ^(ки+)4) ,^у+<  ¹⁰,   ₍₁₆₎

где

к

Е (и⁺) =exp ( ^

arcsin

2Ги+ - 3

-

Q = V 3² + 4Г, у = arcsin(-3/Q), 3 =

Q

Q w Рг

У)) ,

^p W ^C p ^T w ^и т

Р_г^1/3и2 ,  = 2c_pT w

.

Для такого профиля скорости алгоритм граничного условия «закон стенки» устроен следующим образом. На каждой итерации по значению у+ определяются параметры ит, k+ ,и+ ,у+, как описано выше. Величина и+ (у+) = Аи+ вычисляется по формуле Колебрука-Григсона (4) с к = 0.4. Из уравнения (10) получаем и+ (У+ + У+) = и+ + п+ (у+3

Дальше вычисляется невязка уравнения (16).

R = (у⁺ + у + ) - RHS ( u + (у⁺ + у+)),

где RHS (и+(у⁺ + у+)) - правая часть уравнения (16). Другие шаги такие же, как в вышеописанном алгоритме.

Для тестирования описанной методики была разработана вычислительная программа на неструктурированной сетке. В программе используется схема второго порядка. Описание тестов и результаты тестирования представлены ниже.

5.    Обтекание шероховатой пластины5.1.    Эксперименты М. Хосни

В 1991, 1993 гг. в университете штата Миссисипи М. Хосни с коллегами [8, 9] проводил эксперименты для измерения и вычисления теплопередачи на шероховатой стенке в турбулентном пограничным слое.

В экспериментах были рассмотрены все три режима влияния шероховатости, включая режим аэродинамической гладкости, переходный режим и режим с полным проявлением шероховатости. В целом, было рассмотрено четыре поверхности: одна гладкая и три шероховатых. Для моделирования шероховатости на поверхностях располагались полусферы с диаметром D = 1.27 мм на расстоянии друг от друга L = 2D, 4D, 10D соответственно (рис. 6). Длина пластины составляла 2.4 м. В этих работах не представлены конкретные начальные условия набегающего потока, поэтому в данной работе задавались параметры, описанные в [11].

В результате эксперимента вычислялись коэффициент трения:

^T w

^С/   2 Р^и^

и число Стантона:

St =-------.

p^U^C p (T w - T^)

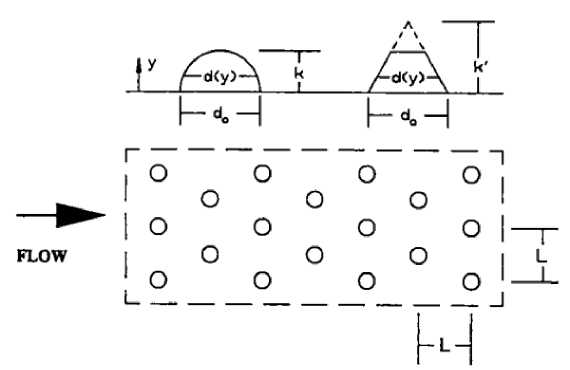
Рис. 6. Шероховатая пластина. [8]

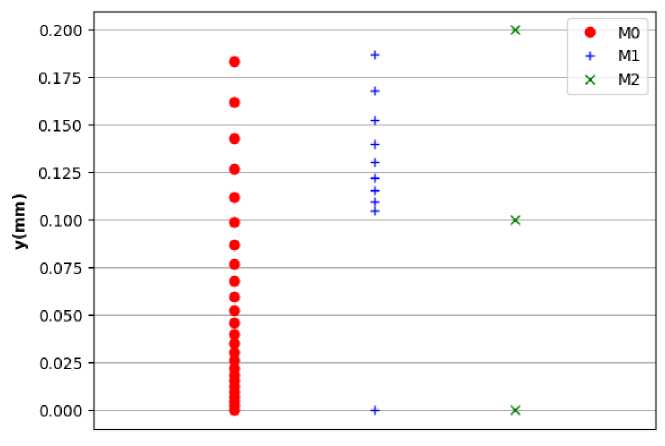
Рис. 7. Расчетные сетки

Для верификации метода, проведены расчеты на. подробной сетке МО и на. двух грубых сетках Ml и М2 (рис. 7).

Эксперимент 1

Рассмотрим эксперимент на пластине с L/D = 2. Начальные условия набегающего потока U^ = 58.0 м/с, Т^ = 28.56 °C, Р^ = 101325.0 Па. Температура поверхности постояна и равна 45 °C. Эквивалентная песочная высота неровности равна k_s = 1.58 мм, к + ~ 300 -соответственно режим полного проявления шероховатости.

Для граничного условия «закон стенки» используются два. варианта, профиля скорости с обозначениями wll - профиль (16), wl2 - профиль (12).

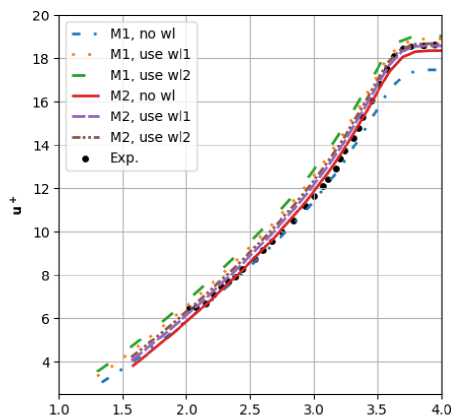
На рис. 8 представлен профиль скорости в сечении ж = 0.86 м. Коэффициент трения и число Стантона, представлены на. рис. 9, 10. Для сравнения на. этих рисунках также представлены результаты модификации Боинга модели Спаларта-Аллмараса [1]. На хорошей сетке МО видна разница между нашим результатом и результатом модификации Боинга, при этом оба. результата, не превышают доверительный интервал эксперимента. На сетке Ml расчетные результаты без использования закона, стенки менее точные. Видно, что использование граничного условия «закон стенки» позволяет повысить точность решений на. обеих сетках Ml и М2, при этом оба профиля скорости wll, wl2 дали близкие результаты.

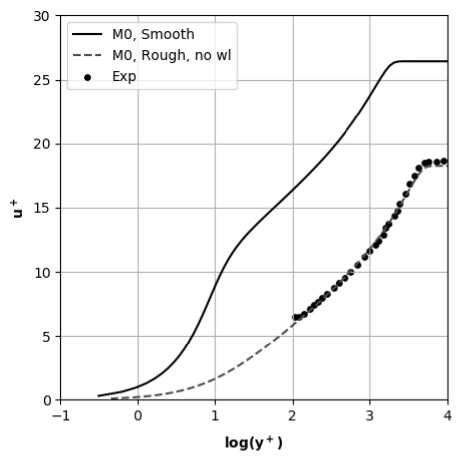
Рис. 8. L/D = 2: Профиль скорости

log(y +)

QI2

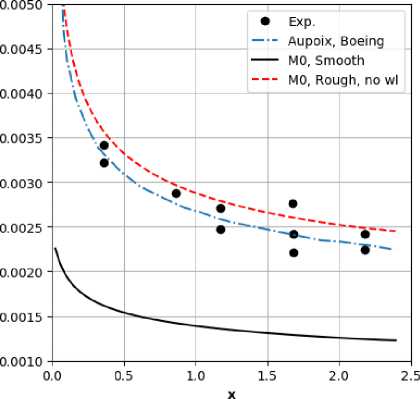
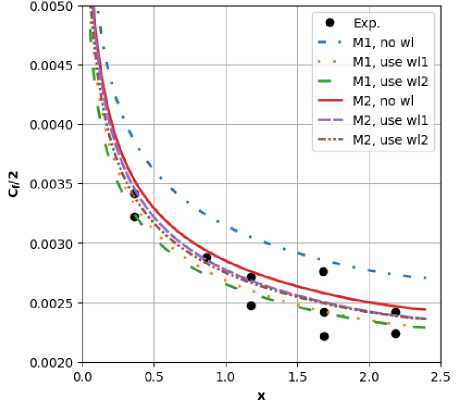
Рис. 9. L/D = 2: Коэффициент трения

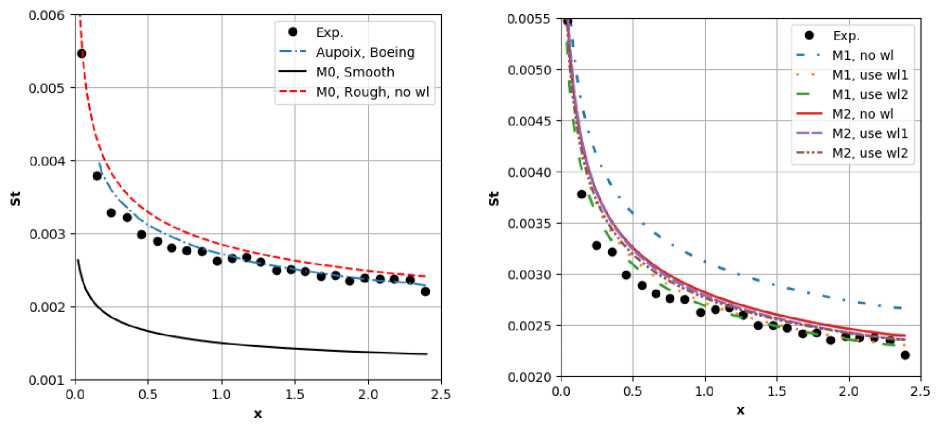
Рис. 10. L/D = 2: Число Стантона

Эксперимент 2

Рассмотрим второй эксперимент на пластине с L/D = 4. Эквивалентная песочная высота неровности равна 0.38 мм, к+ ~ 60, т.е. мы имеем переходный режим, когда часть элементов шероховатости выступает из вязкого подслоя и начинает оказывать влияние на характеристики течения, создавая дополнительное сопротивление.

Коэффициент трения и число Стантона представлены на рис. 11, 12. В этом случае сетка Ml дала неточный результат даже при использовании закона стенки. Результаты с использованием профиля скорости wll на сетке М2 сильно отличаются от результата на хорошей сетке МО. Причиной больших погрешностей при применении профиля wll могут быть как особенности переходного режима, так и использование формулы по данным Колебрука для определения сдвига Аи+ и у+.

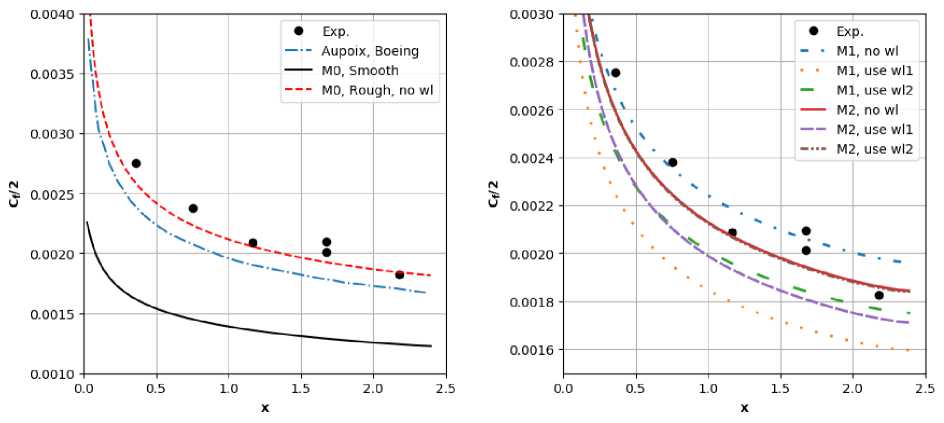
Рис. 11. L/D = 4: Коэффициент трения

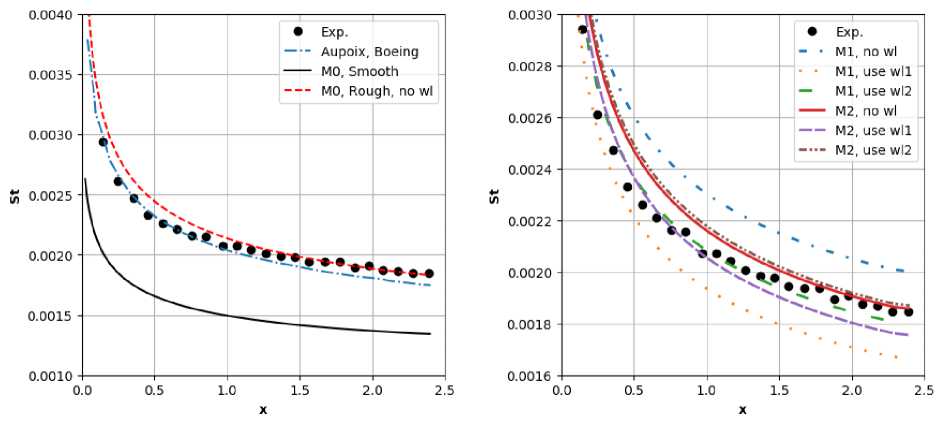
Рис. 12. L/D =4: Число Стантона

5.2.    Эксперименты Дж. Хеалзера

В 1974 году Дж. Хеалзер с коллегами [10] проводил эксперимент для изучения турбулентного пограничного слоя на шероховатой пластины при разных скоростях набегающего потока. В этой работе мы будем рассматривать случай со скоростью U^ = 73.8 м/с. Другие параметры заданы как в эксперименте М. Хосни. На пластине, в отличие от предыдущих экспериментов, расположены сферы с диаметром 0.635 мм. Эквивалентная песочная высота неровности равна 0.79375 мм, что соответствует к+ ~ 175, т.е. режиму полного проявления шероховатости.

На рис. 13 показано сравнение нашего результата с данными эксперимента и результатами модели SA в работе [2]. Видна большая разница между расчетным коэффициентом трения и данными эксперимента, возможно, из-за формы элементов шероховатости. Для числа Стантона наш результат на сетке М2 хорошо совпадает с данным эксперимента, но сильно отличает от результата [2]. Возможной причиной может быть задание различных условий набегающего потока в расчетах, так как эти условия конкретно не было описаны в работах [10] и [2].

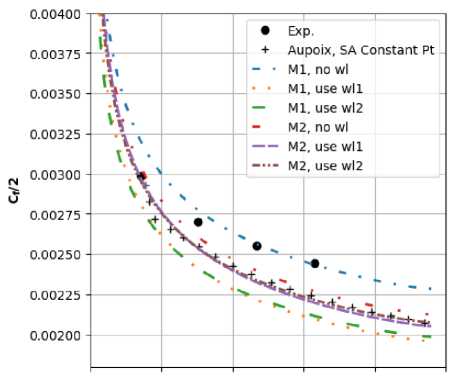
0.0        0.5        1.0         1.5        2.0        2.5

X

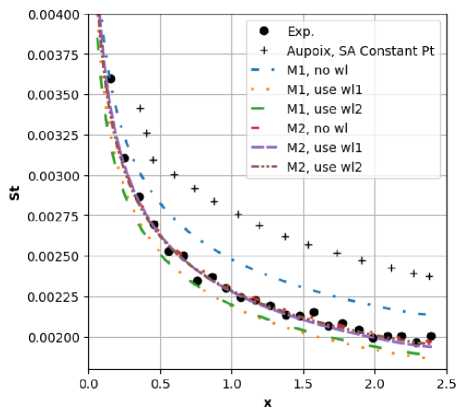
Рис. 13. Эксперимент Дж. Хеалзера

6.    Заключение

Расчетное исследование показывает большое влияние шероховатости на профиль скорости, коэффициент трения и число Стантона.

Использование граничного условия «закон стенки» позволяет повысить точность решения на грубой сетке. При этом использование профиля скорости wl2 позволяет получить более точный результат.