Граничные потенциалы биоколлоидных частиц: количественный анализ

ВВЕДЕНИЕ                    нивается величиной 60 e [5]. Хотя модельные сис-

Хорошо известно, насколько важную роль играют электрофизические параметры, в том числе заряд и потенциал поверхности, дипольный и электрокинетический потенциалы, свойства тонких пограничных слоев такие, например, как поляризуемость (диэлектрическая проницаемость) и электрическая емкость, а также и вязко-упругие свойства вещества на границах раздела в коллоидных системах. Это еще более существенно для водных биоколлоидов, т. е. клеток и клеточных органелл, субклеточных частиц (например, протопластов) и модельных систем (липосом) различного происхождения [1–3]. Поверхностные потенциалы частиц могут быть положительными за счет протонирования или отрицательными при диссоциации поверхностных радикалов (например, карбоксилов HCOO-). Максимальная плотность связанного отрицательного поверхностного заряда (например, для бислоя на основе фосфатидилсери-на), определяющая поверхностный потенциал, оценивается [4] величиной 0.1 ^ 0.2 Кл • м-2, что соответствует поверхностному заряду микронной частицы, равному примерно 107 e, и поверхностной плотности — один элементарный заряд на 100– 200 Å2. Свободный заряд, определяющий дзета-потенциал, значительно меньше. В частности, свободный заряд мицелл поверхностно-активных веществ (например, додецилсульфата натрия) оце- темы в силу своей относительной простоты позволяют изучать многие важные процессы и свойства (функционирование ионных каналов в мембранах, действие порообразующих токсинов и антимикробных соединений и др.), суспензии интактных клеток гораздо сложнее. Многие экспериментальные технологии, связанные с исследованием мембранной биоэнергетики, например, флуоресцентные или потенциометрические [6] измерения трансмембранного потенциала клеток с использованием проникающих (липофильных) ионов, требуют детального знания электрофизики клеточной периферии. С другой стороны, такие параметры, как дипольный, поверхностный и дзета-потенциал недоступны прямому измерению. Это порождает неточность оценок и последующих расчетов. Например, поверхностный потенциал водных микроскопических капель на границе с воздухом принимался равным 300 мВ [7]. Общая оценка величины поверхностного потенциала частицы ϕs располагалась в пределах 0.25 < 9s < 0.36 В , причем нижняя граница, как предполагалось, соответствовала скачку потенциала на двойном электрическом слое, а верхняя — значению, вычисленному на основе выражения ф8 = n8pr / £0 (n, 8, pr — соответственно объемная концентрация диполей, толщина двойного слоя и проекция дипольного момента на радиальное направление сферической частицы). Таким образом, поверхностный потенциал атмосферных водных капель был принят равным ф5 = 0.3 В, но этого было недостаточно для анализа устойчивости коллоидной системы. Дипольный потенциал полярных групп липидов и ассоциированных с ними молекул воды в пограничном слое внутри липидных мембран оценивался в пределах от 400 до 700 мВ [4], но эту оценку было трудно сопоставить с такими основными параметрами, как трансмембранный и поверхностный потенциалы. В целом задача состоит в детальном анализе потенциального периферического профиля частиц, активных или неактивных биологически. Таким образом, аналитические приемы остаются актуальными.

ГРАНИЧНЫЕ ПОТЕНЦИАЛЫ ЧАСТИЦ

Аналитическое решение для потенциала ϕ у поверхности частицы (клетки) дается интегрированием уравнения Пуассона—Больцмана A p = - ( 1 ££ 0 ) Р ( г ) , где р ( г ) — объемная плотность заряда для одновалентного симметричного электролита, определяемая выражением

р( г ) = en {exp [-ep (г)/(kBT)]- exp [ ep (r)/(kBT)]}.

Первое интегрирование уравнения по Гюи— Чапмену для частного случая слабо заряженных частиц, т. е. при условии ep ( г )( k_BT ) « 1, или p ^ 25 мВ, общеизвестно и записывается в виде

• - d p = 8 nk B T sh Г ep d г \ ££ 0 ( 2 к в Т

Второе интегрирование явилось предметом многочисленных работ и в наиболее простом случае сводилось к линеаризации sh (epf (2kBT)), что в конечном счете привело к известному приближению Дебая—Хюккеля. Существенно отметить, что в приближении Дебая—Хюккеля ионы электролита не имеют собственных размеров, т. е. считаются точечными и не взаимодействуют. Интегрирование в области a < г < да недоступно, с одной стороны, в пределах двойного электрического слоя на поверхности г = а, поскольку неизвестна его толщина. С другой стороны, интегрирование для суспензии частиц доступно на расстоянии от поверхности, не превышающем половину среднего расстояния между частицами b = lm /2. Еще две границы определяются поверхностью гидродинамического скольжения (slipping plane), элек-трокинетическим радиусом rc и соответственно дзета-потенциалом частиц ζ . Кроме того, поскольку ζ-потенциал существенно меньше, чем поверхностный потенциал ϕs , разложение больц-мановских экспонент в степенной ряд в области гс < г < да значительно точнее, чем в области а < г <да. Поэтому sh(ep(2kBT)) = ep(2kBT) и dϕ   8nk T e        2ne2

--= --- ^B ---d г =, ------ d г = x d г ϕ     εε ₀   2 nT      εε ₀ k_BT

2 ne ²

• ( 88 ^£k 0 k_BT J’

где x = 1 I D — параметр Дебая—Хюккеля ( I D — дебаевский радиус экранирования). Существенно отметить, что величина радиуса экранирования при заданной температуре зависит только от концентрации добавленной соли. Интегрирование приводит к выражению

p ( г ) = Z exp [- x ( г - г с ) ] .

Это выражение при г >  г_с показывает, что чем больше концентрация электролита n , тем быстрее убывает потенциал при удалении от электрокине-тической поверхности г = г_с . Однако оно не содержит никакой связи с поверхностным потенциалом и в целом с потенциальным профилем клеточной периферии.

Кулоновское взаимодействие противоионов положительной полярности с отрицательно заряженной поверхностью (физическая адсорбция) частицы приводит к нарушению электронейтральности электролита. Таким образом, за основу для анализа можно использовать неравновесную концентрацию противоионов А n ₊ ( г - а ) / n , выраженную в относительных единицах.

Для описания хода потенциала в ближней периферической области используем некоторые приемы, характерные для физики твердого тела. Например, для ионных кристаллов того же состава, что и типичный биологический электролит (NaCl), потенциал взаимодействия ионов в решетке записывается в виде [8]

p =

A ± e_ rⁿ r ^,

где λ — постоянная решетки, равная для NaCl примерно 5.5 А. Положительное (отталкивательное) слагаемое при n —10 очень сильно зависит от расстояния и определяет жесткость решетки кристалла, однако полная энергия сил сцепления в кристалле определяется в основном кулоновским взаимодействием (вторым слагаемым). Это справедливо и для энергии сцепления катионов с отрицательно заряженной поверхностью биологических частиц при условии, что среднее расстояние между ионами не слишком мало. Если исходить из известных [4, 6] измеренных значений поверх- ностной плотности заряда с = (0.1 ^ 0.2) Кл/м2, т. е. из расчета 1 элементарный заряд на 100– 200 квадратных ангстрем, что соответствует линейному размеру 10–15 Å, то предположение о кулоновском характере связывания справедливо. Weiss [9] в своем обзоре вводит в выражение для поверхностной плотности заряда

• ^с = [ 1 + ( 1 - ^а ) 12 ] ( 8 ^ss о nk B T ) ^V 2 sh^

параметр 0 <  а <  1, показывающий долю поверхности, которая не может быть занята противоионами. Приведенное выражение, строго говоря, получено при измерениях дзета-потенциала масляных капель в водных растворах поверхностно-активных ионов. При этом не делалось различий между электрокинетическим и поверхностным потенциалами. Для гетерогенных частиц биологического происхождения можно принять, по-видимому, а = 0. Расчет для значений ф_а = 120 мВ; n = 0.0029M • l ^{- 1} = 17.5 • 10²³м ^{- 3}; s = 80; T = 298 К дает поверхностную плотность заряда частиц с = 0.064 Кл • м ^{- 2}, достаточно близкую к приведенным выше значениям.

Для дальнейшего анализа необходимо связать электрокинетический радиус r_c и дзета-потенциал ζ , а также выяснить связь между дзета-потенциалом и потенциалом поверхности частицы ϕ_a (обозначение ϕ_a равнозначно использованному ранее ϕ_s ). Наибольшие трудности связаны с анализом ближней периферической области клетки (частицы), граничащей с поверхностью частицы. Эти трудности еще более характерны для так называемого штерновского двойного электрического слоя. В этой очень тонкой области концентрация противоионов и, следовательно, напряженность электрического поля становятся экстремально высокими. Понятно, что в этой области разложение потенциальной функции в степенной ряд неприемлемо.

Для оценки толщины двойного слоя, рассматриваемого как квазикристаллическая среда, целесообразно использовать величину сжимаемости двойного слоя, которая также определяется кулоновским взаимодействием. Для кристаллов NaCl измеренная экспериментально сжимаемость равна K = 3.3 •10-11м2 • N-1, а ее обратное значение соответствует давлению 3 •1010Пa. Отметим, что сжимаемость дистиллированной воды при 20°C (0.47 •10-9м2 • N-1) примерно в 14 раз больше, а давление (2 • 109 Пa) во столько же раз меньше. Таким образов, при адсорбции физическая среда двойного слоя представляет собой, по-видимому, достаточно упругую квазирешетку противоионов вместе с противолежащей матрицей связанного поверхностного заряда частиц, заполненную водой. Ясно, что сжимаемость ближайшего к поверхности слоя противоионов должна быть больше сжимаемости воды, а соответствующее давление — меньше (1.4 •107Пa). Это давление может быть получено на основании соотношения (VK) = ss0Аф2/(232), определяющего объемную плотность электростатической энергии слоя (конденсатора) толщиной δ с разностью потенциалов между обкладками слоя, равной Аф. Объемную плотность энергии можно получить также из выражения с2/(2ss0). Сравнение обоих выражений для плотности энергии определяет равенство 3 = ss0Афс. При уже использовавшихся значениях Аф = фa = 120мВ; с = 0.064Кл • м-2 расчет дает 3 = 13 А. Отметим, что толщина 3, исходя из очевидных соображений, оценивается пропорциональной поверхностному потенциалу и обратно пропорциональна поверхностной плотности заряда. Если поверхностную плотность заряда, как уже было отмечено, считать равной с = 0.1 ^ 0.2 Кл • м-2, то получаем 3 = 4 ^ 8 А. Точно так же, если принять фа = 60 мВ (например, для эритроцитов), то 3 = 6.5 А. В дальнейшем будем использовать значение 3 = 6 А, обоснованное ниже.

ГРАНИЧНАЯ КОНЦЕНТРАЦИЯ ИОНОВ

Запишем аналитическое выражение общего вида для граничной концентрации противоионов А n + ( r - a ) / n + ( n + — равновесная концентрация ионов в невозмущенном частицами электролите), не связанное с больцмановской силовой функцией:

А n. ( r - a )      q p ,    „     „      .

---------- = -^-+ P 2 (q < 0;p > 0;r > a), n +       r - a (r - a)

где a — радиус частицы; q , p — параметры, имеющие размерность соответственно длины и квадрата длины. Минимальное значение разности r - a = 3 определяет толщину двойного слоя. Первое (отрицательное) слагаемое в правой части определяется кулоновским взаимодействием "заряд—заряд", тогда как второе (квадратичное) — заряд-дипольным взаимодействием. При этом выполняется условие сохранения числа ионов раствора при поляризации электролита заряженными частицами.

Принципиально важно, что потенциальная функция может быть задана аналитически очень близко к поверхности, например, с точностью, определяемой собственными размерами ионов (1– 2 Å ).

Кулоновская адсорбция катионов уменьшает свободную энергию поверхности, но ориентация поверхностных постоянных диполей в сильном электрическом поле двойного слоя, прежде всего гидроксилов О–H растворителя (воды) с дипольным моментом p_s = е • l d = 3.34 • 10 ^{- 30}Кл • м (1 дебай), уменьшает энтропию поверхности и соответственно действует противоположным образом, т. е. увеличивает свободную энергию. Квадратичное быстро убывающее слагаемое, а также и слагаемые более высоких порядков, можно рассматривать также, как поправочные члены представления функции 1/ ( r - a ) степенным рядом около значения r = a , соответствующего поверхности частицы. Если использовать для сравнения энергий взаимодействия выражения е ²Д s ₀ r ) (кулоновское), ер/ ( s ₀ r ² ) (заряд—постоянный диполь) и р ²Д s ₀ r ³) (постоянный диполь—постоянный диполь, потенциал Кеезома), то при значении 5 = 6 А эти энергии соотносятся как 1250:50:1, т. е. с сильным преобладанием кулоновского взаимодействия. Преобладание кулоновского взаимодействия и соответственно соотношение 35:8:1 сохраняется и при значении 5 = 1 А . Отметим в связи с этим, что условие A п ₊ / п ₊ = 0 достаточно точно соответствует равенству обоих слагаемых в правой части записанного выше аналитического выражения. Кроме того, ясно, что возрастание концентрации противоионов означает возрастание потенциала, ограниченное значением потенциала поверхности частицы или равное этому потенциалу.

Достоверная оценка толщины двойного слоя начинается очень давно [10] и представляет, как уже было отмечено, главную трудность. Прежде всего по причине того, что граница между частицей и средой ни в коем случае не является геометрически точной. Кроме того, реальная граница может быть многослойной и достаточно толстой. Например, в трехслойной мембране бактериальной, животной или растительной клеток периплазма разделяет два поверхностных слоя (внутренний и внешний) по (2 ^ 3) нм толщиной каждый. Толщина двойного слоя в модели Штерна [11] принята равной радиусу ионов электролита, т. е. 1–2 Å. В качестве минимальной оценки может быть принята длина ld диполя O–H, равная примерно 0.1 нм (1Å). Дебай и Хюккель оценивали толщину двойного слоя величиной дебаевского радиуса экранирования lD , т. е. несколько десятков ангстрем, что в целом справедливо для больших частиц. При большой толщине двойного слоя принято говорить о плотной и относительно неплотной частях слоя, хотя это и противоречит исходной концепции Гельмгольца—Перрена. В целом все геометрические трактовки двойного слоя, кроме дебаевской, кажутся несостоятельными по причине неясности их физического смысла.

Оптимальной оценкой, по-видимому, следует считать длину Ландау lL = е2Д kBT), которая соответствует термодинамическому равновесию адсорбированного слоя ионов [12]. Следовательно, равенство r - a = lL соответствует, как уже было отмечено выше, равенству заряд-зарядовой и за-ряд-дипольной компонент энергии взаимодействия электролита в целом, т. е. добавленной соли и растворителя, с поверхностью частицы. Отношение е2ДkBT) на самом деле имеет размерность электрической емкости, которая в электростатической системе единиц CGS измеряется в сантиметрах (см). Таким образом, при температуре T = 300К получаем 1L = 5.57-10-6см = = 0.618•Ю-^Ф. Это значение соответствует линейному размеру 5 = lL S = 6.94 •10-8см в системе единиц CGS и тому же размеру 5 = = 1LД4nss0 ) = 6.94 •10-10м = 0.7нм(7А) — в универсальной системе единиц. Хотя такое значение длины δ только условно можно считать толщиной двойного электрического слоя, оно дает реальное представление о размерах (толщине) граничной области частицы. При этом можно полагать, что поляризуемость внутренней среды двойного слоя определяется макроскопическим значением диэлектрической проницаемости (для воды s = 80). Полученное значение длины близко к значению постоянной кристаллической решетки кристалла NaCl, равной X = 5.5 А. Близость этих значений объясняется тем, что в экстремально сильном электрическом поле двойного слоя (106 ^ 107 В • см-1) должны происходить структурные изменения как ионных зарядов добавленной соли, так и дипольных компонентов растворителя. Структурные изменения ионных зарядов определяются тенденцией к кристаллизации соли на поверхности частицы, а изменения дипольных компонентов означают выстраивание элементарных диполей растворителя по силовым линиям поля с соответствующим увеличением дипольного момента. Таким образом, как уже отмечалось, вся структура представляет собой квазикристалличе-ский каркас, заполненный хорошо поляризующейся средой (вода). В дальнейшем мы будем считать началом отсчета значение радиуса r = a + 6 А. Это же значение определяет и толщину двойного электрического слоя, т. е. 5 = 6 А. При этом теряют смысл устоявшиеся различия между плотной и неплотной частями двойного слоя.

Взаимная ориентация постоянных диполей в теории Кирквуда—Фрелиха [13] определяется неравенством ( 1 + z cos у ) — ( 1 + z ) , где z — число ближайших соседей одно го пр оизвольно выбранного диполя; величина cos γ является мерой "ближнего порядка" для полярной жидкости. Можно полагать, что в экстремаль но си льном поле двойного слоя среднее значение cos γ приближается к 1, а неравенство — к равенству. Поэтому в среднем на длине 5 = ( 5 ^ 7 ) А может разместиться 5–7 выстроенных в цепочку диполей O–H.

Таким образом, для однозарядного симметричного электролита (NaCl) оба слагаемых в правой части представленной выше формулы для безразмерной концентрации An + /n могут быть также выражены в безразмерном виде   q(rr - a)

и p /( r - a ) ², т. е. q = 5 и p = 5 • l_p , где l_p >  l d .

Для построения зависимости A n ₊ ( r - a ) необходимо задаться дополнительно величиной масштаба расстояния от поверхности частицы. Наиболее удобно такой величиной считать электроки-нетический радиус r_c , который может быть получен экспериментально при измерениях дзета-потенциала. Значения радиуса r_c в зависимости от концентрации электролита обсуждаются ниже.

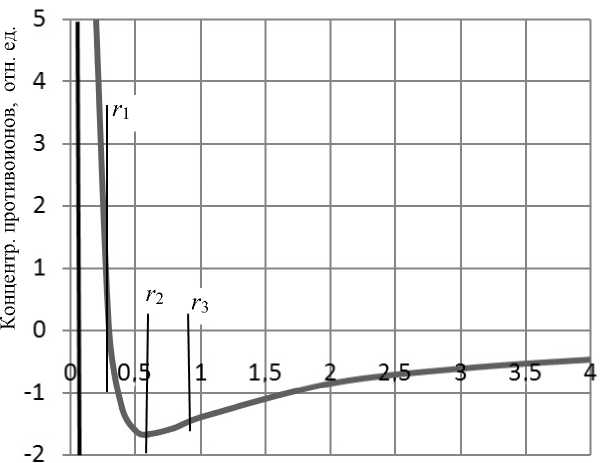
На рис. 1 представлена типичная зависимость концентрации противоионов A n ₊ ( r - a ) / n ₊ при значениях безразмерных параметров q = - 2, p = 0.6, показывающая, что концентрация ионов вблизи двойного слоя очень быстро возрастает. При построении зависимости электрокинетиче-ский радиус, отсчитанный от внешней границы двойного электрического слоя, был выбран равным r c = 6 нм (60 Å ).

( r – a ), отн. ед.

Рис. 1. Безразмерная концентрация противоионов в функции расстояния до поверхности частицы.

Безразмерные параметры: q = - 2; p = 0.6; масштаб по горизонтальной оси 10 нм (100 Å ); жирная линия вблизи вертикальной оси показывает границу двойного слоя; r ₁ определяется из условия

A n ₊( r - a ) = 0; r ₂ определяется из условия [a n ₊( r - a ) ] = 0 (минимум потенциальной функции); r ₃ определяется из условия [a n ₊( r - a ) ] = 0 (условная граница потенциальной ямы)

Отметим, что при учете в разложении функции 1/ ( r - a ) слагаемых порядков выше второго приближение к нулю происходит быстрее, чем это следует из рис. 1. Выделим теперь характерные точки периферической области вблизи от поверхности частицы.

• а)    Точка нуля функции A n ₊ ( r ) = 0 , откуда следуют равенства r - а = - q/p и соответственно r = а + n8, где n = 5 ^ 7.

• б)    Точка r ₂ минимума функции A n ₊ ( r - а ) , определяемая из условия d n ₊ ( r - а ) /d r = 0, т. е. r ₂ - а = - 2 p / q и соответственно r ₂ = а + 8 + r c .

• в)    Точка перегиба, определяемая из условия d² n ₊ ( n 3 - а ) /d r ² = 0, т. е. n 3 - а = - 3 p/q и соответственно r ₃ = а + 8 + r_2p .

Таким образом, потенциальная функция может быть задана аналитически очень близко к поверхности с точностью до толщины двойного электрического слоя δ или еще меньше.

Сформулируем условия, которые могут считаться исходными для оценок и расчетов параметров ближней периферической области частицы.

Первое из этих условий соответствует сохранению числа ионов раствора при поляризации электролита заряженными частицами. Это условие формулируется следующим образом:

описывается общим выражением вида

dVchem = k,d [ln ( n +( r - а ))] = дГn, (r - а)l/dr

= k» [ + f ]    dr,

n + (r - а)

Г а + rc

1 а + 8

q + p

r - а (r - а )2

4nr ²d r =

Г ^{а +} b m /2

J а + r_c

q

p

r - а (r - а )2

4 πr ²d r ,

где b_m — среднее расстояние между частицами в суспензии. Интегрирование приводит к выражению

а ( аq + 2 p ) l

2       (         1 А

[ n ГТ + ^p - Sb™ q 1 = 0, \ 8     8    )

bδ m

для использования которого необходимо задаться значениями r_c и δ .

Второе условие определяется характером изменения химического потенциала противоионов. Точка пересечения кривой с асимптотой A n ₊ ( r - а ) = 0 определяет единственную поверхность в ближней периферической области частицы, на которой концентрация противоионов равна равновесному (невозмущенному) значению n ₊ . Изменение химического потенциала противоионов

где коэффициент k _ϕ для однозарядных ионов при T = 298 К равен k » = k B T/e = 25.7 мВ .

Поскольку элементарные приращения химического потенциала при переходе через эту поверхность имеют одинаковые знаки, ясно, что точка пересечения кривой A n ₊ ( r - а ) с асимптотой A n ₊ = 0, т. е. радиус r 1 = а + n8 соответствует неустойчивости (скольжению) коллоидной частицы и появлению вращательных степеней свободы.

Третье условие соответствует минимуму кривой A n ₊ ( r - а ) и поверхности радиуса r ₂ = а + 8 + r c . При переходе через эту поверхность приращения химического потенциала имеют разные знаки, что и объясняет устойчивость этой гидродинамической границы при поступательном движении в неполяризованном электролите частицы вместе с адсорбированным слоем противоионов.

Для биологически активных частиц (например, клеток или органелл) можно связать поверхностный потенциал ϕ_a с клеточным трансмембранным потенциалом A »_M , генерируемым в физиологически активной части области клетки (т. е. на плазматической мембране) и таким образом связать все наблюдаемые электродиффузионные эффекты с трансмембранным потенциалом клеток. Кроме того, отметим, что поверхностный потенциал ϕ_a в общем случае состоит из пассивной части, связанной с потенциалобразующими свойствами клеточной поверхности, и из активной части, являющейся, условно говоря, "периферическим выражением" трансмембранного потенциала, генерируемого в более глубоких слоях клеточной периферии. Такие параметры, как мембранный потенциал, могут сильно различаться в зависимости от вида клеток и огромной совокупности параметров (ионная сила раствора, рН, условия роста клеток, фазы клеточного цикла и др.). Можно, однако, сформулировать некоторые общие подходы, характерные в целом для коллоидных систем.

СВЯЗЬ ПОВЕРХНОСТНОГО

И ЭЛЕКТРОКИНЕТИЧЕСКОГО ПОТЕНЦИАЛОВ

Приведем два подхода.

Способ I. Движение сферической частицы вместе с адсорбированным слоем противоионов можно рассматривать либо как движение некоторой эквивалентной частицы радиуса r_c с поверхностным потенциалом ф ( r c ) , либо как движение среды относительно неподвижной сферической полости радиуса r_c , имеющей поверхностный потенциал ф ( r c ) . Поскольку в действительности такие движения эквивалентны, то должно выполняться равенство

ф ( a ) ^- ф ( r c ) = ф ( r c ) ^- ф ( ” ) , из которого следует (при ф ( да ) = 0) выражение

ф ( rc ) = ^ = 2 ф( a )= 2 фа .

Если использовать выражение для дзета-потенциала, основанное на дебаевском приближении, получим равенство откуда следует уравнение exp [-(rc -а) ilD ]=2а •

Представив r c в виде суммы r c = а + kl_D ( к >  0), запишем далее

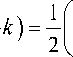
• 1    + D D I . а )

Решив это уравнение графически (рис. 2), получим, что величина k должна находиться в пределах 0 <  к <  0.7 .

Для больших частиц, т. е. при lD/а ^ 0, получаем максимальное значение к = 0.7. В табл. 1 представлены результаты расчетов электрокине-тического радиуса в зависимости от радиуса частицы a . Здесь же представлены значения электро-кинетического радиуса в зависимости от приведенного радиуса а + 5 ( 5 = 0.6 нм ) .

- X r — а) q e ⁽ c )

—

4 п££ 0 r c 1 + ха

1 q 1 --.-----------------------

2 4 п££ 0 а 1 + ха

( X = 1 I d ),

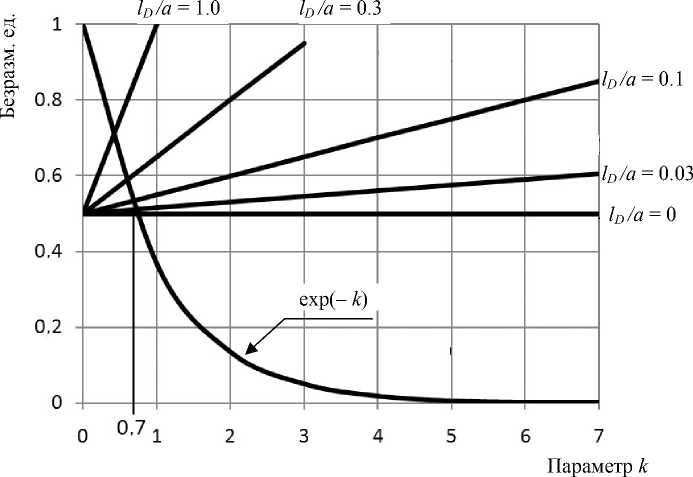
Рис. 2. К расчету радиуса гидродинамического скольжения (способ I).

Показано семейство прямых ( 1 + kl D/ а ) /2 в функции отношения l_D / а ; точки пересечения с экспонентой exp ( - к ) дают значения параметра к

Табл. 1. Результаты расчетов электрокинетического радиуса в зависимости от радиуса частицы a (способ I)

а , ( а + 5 ) ,нм	lD ,нм	k	klD ,нм	r c ; ( r c + 5 ) ,нм
3; (3.6)	3	0.375	1.12	4.12; (4.72)
30; (30.6)	3	0.632	1.9	31.9; (32.5)
100; (100.6)	3	0.673	2	102; (102.6)
1000; (1000.6)	3	0.695	2.1	1002; (1002.6)

Способ II. Если рассматривать функцию ф(r) как некоторое статистическое распределение (функцию плотности вероятности), каким она в действительности и является, то ясно, что поверхность r = rc разделяет частицу вместе с адсорбированным слоем и электролит, если вероятности локализации некоторого иона ближе или дальше от границы r = rc одинаковы. Тогда должно выполняться равенство rc                 m jф(r)dr = jф(r)dr, a                  rc означающее, что r = rc есть медиана распределения ф(r). Если использовать опять дебаевское приближение, то получаем rc ^-xr       т --xr j e_ dr = j e— dr, a r         rc r m - xr       m - xr       m - xr или            [----dr - [----dr = [d rrr a                  rcr и после замены xr = P равенство m - p          m

J — d p = 2 J — d p .

a l D ^ρ          r c l D ^ρ

Вводя функцию Эйлера m 1

- Ei ( - x ) = j—d t   (0 <  x )

x и правило для вычисления интеграла Эйлера Ei (-x) при больших значениях аргумента

- x

Ei (- x ) = - F1 —, x в котором

1! 2!   3!

F1 = 1 — + — - — + ^, x x2   x3

запишем исходное условие равенства потенциалов по обе стороны границы r = r c в виде

Ei ( - rdl D ) = 2 Ei ( - a/l D ) .

Зависимость r_c a в функции a l_D представлена на рис. 3 и показывает, что с ростом отношения a l_D гидродинамический радиус частицы быстро приближается к ее геометрическому радиусу.

Результаты расчетов, выполненных в соответствии с формализмом способа II при тех же исходных данных, что и для способа I, приведены ниже в табл. 2. Сравнение обеих таблиц показывает достаточно близкое сходство этих результатов. Некоторое различие значений r_c , вычисленных первым и вторым способами, определяется видом функции ф ( r ) .

Если от распределения потенциала в ближайшем окружении частицы rc a

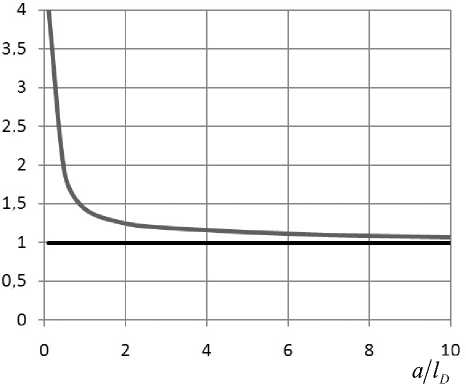
Рис. 3. К расчету электрокинетического радиуса (способ II)

Табл. 2. Результаты расчетов электрокинетического радиуса в зависимости от радиуса частицы a (способ II)

а ,нм	lD ,нм	a lD	rc a	rc ,нм
3	3	1	1.44	4.32
30	3	10	1.07	32.1
100	3	33.3	1.025	102.5
1000	3	333	1.002	1002

• - х ( r — a )

ф( r ) =          • e

4n££ 0 r 1 + %a для сравнительно крупных частиц, т. е. при Xa »1 и r = a , перейти к экспоненциальному распределению потенциала

ф(r) = Cexp[-х(r - a)], то в соответствии с исходным равенством rc                     to j ф( r) dr = j ф( r) dr a                   rc после интегрирования получим соотношение exp [-x( rc- a )]=2.

Это равенство выполняется, если x ( r_c - a ) = 0.7 и r c = a + 0.7 I D , т. е. в точности совпадает со значением, вычисленным первым способом.

Мы будем считать, что равенство r c = a + 0.7 I D выполняется при экспоненциальном или близком к экспоненциальному распределении потенциала; кроме того, выполняется и соотношение Z = ф_я /2. Таким образом, эти два простых соотношения должны выполняться совместно

' rc = a + 0.7 ID, ‘.Z = (12 ф, что сразу дает возможность связать три важнейших параметра ϕa , ζ, rc . Для этой тройки параметров важно отметить, что электрокинетический потенциал может быть определен экспериментально.

Можно оценить точность расчетов электроки-нетического потенциала. Пусть поверхностный потенциал частиц составляет ф_s = ф_я = 120мВ, а электрокинетический потенциал равен соответственно Z = ( 12 ) ф_s = 60мВ. Тогда произведение

Xr_c = r_c/l D , вычисленное при T = 298К на основании соотношения Овербека [14]

th [ ^zeф s /4 ^k B T ]

Xrc      th [zeZ!4kBT] ’ оказывается равным Xrc = 0.449, а электрокине-тический потенциал — равным Z (rc) = 76.6мВ. Если же использовать равенство rc = a + 0.7ID, то получаем значение Z (rc) = 59.6мВ, по отношению к которому расчет по формуле Овербека дает погрешность, равную 28.5 %.

Используем теперь более точное выражение для штерновского потенциала, полученное [15] в предположении плоского двойного слоя:

У 1 ( ^{r -} r c ) = ^2ln

1 + th ( Z /4 ) exp [- х ( r - r c )

1 - th(Z/4)exp[-X(r - rc)], где y1 , ζ — безразмерные потенциалы, выраженные в долях kBT/e = 25.7мВ (T = 300К), а r отсчитывается от электрокинетической поверхности r = rc, что, очевидно, понижает практическую ценность соответствующих вычислений. Результаты вычислений при n = 0.0029М • л-1; х = = ( 2 ne2/(££0 kBT ))12 = 1.765 •108м-1 (£ = 78.3); 1D = = 1 х = 56.6 A; Z = 60 мВ представлены в табл. 3 (верхняя строка рассчитанных потенциалов). В этой же таблице (нижняя строка) представлены значения потенциала, соответствующие рис. 4. Сравнение значений потенциалов показывает разницу в 2–3 % вблизи от электрокинетической поверхности, возрастающую до 10 % далеко от нее.

Таким образом, остается неопределенность описания потенциальной функции ф ( r ) в ближней периферической области a <  r <  r_c или ( a + 5 ) < r <  r c . Наиболее вероятно считать, что потенциал наружной обкладки двойного электрического слоя (сферического молекулярного

Табл. 3. Результаты вычислений потенциалов

Функция	Расстояние r - r c , А
	0	10	20	50	100	200
У 1 • ( k B T/e ) ,мВ	60.00	48.60	39.85	22.74	9.26	1.58
Значения по рис. 4, мВ	60.00	49.94	41.85	24.63	10.18	1.74

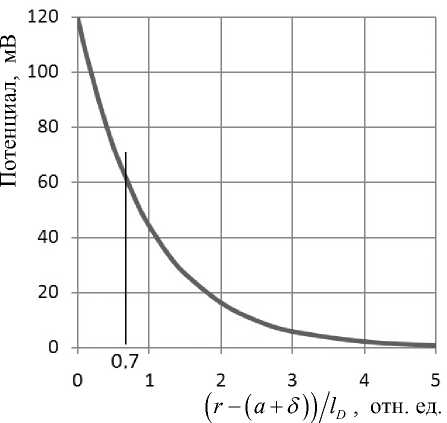
Рис. 4. Зависимость потенциала ф ( r ) от расстояния до поверхности радиуса r = a + 5 сферической частицы.

Дебаевская длина экранирования lD = 56.6 А соответствует значению 1 по горизонтальной оси; расстояние 0.7lD = 40 А (электрокинетический радиус) соответствует дзета-потенциалу Z = 60 мВ конденсатора Гельмгольца), т. е. поверхности r = a + 5, равен поверхностному потенциалу частицы ϕa . Тогда уравнение потенциальной функции должно быть записано в виде

ф(r) = Фа exp[-(r-(a + 5))/lD].

На рис. 4 эта зависимость представлена графически; там же показана гидродинамическая граница частицы r c = a + 0.7 l_D , выраженная в долях дебаевского радиуса экранирования. При этом потенциал отсчитывается от физической границы частицы r = a , потенциал которой считается нулевым, а в пределах двойного электрического слоя линейно возрастает до значения ф_я = 120мВ. Это соответствует напряженности поля в двойном слое, равной 2 - 10 6 В • см ^{- 1}.

Отметим также, что второе приближение штер-новского потенциала получено Духиным [10] и выражается суммой y2 = y1 + (Аy1 ]^xr)), где Ау1 описывается функцией вида th (У1/4) th (Z/4)

А y. = 1sh —

th² ( Z /4 ) - th² ( y 1/ 4 ) + 2ln

При r = r c получаем y 1 = Z и, как и следовало ожидать, А у 1 = 0. Кроме того, для больших частиц, т. е. при xa ^ 1, слагаемое А у 1 несущественно. С другой стороны, это приближение, как и во всех других случаях, неприменимо к анализу ближней периферической области частицы.

ВЫВОДЫ

Главный результат статьи состоит в том, что в ней обоснована близкая к реальности структура двойного электрического слоя, граничащего с поверхностью коллоидной частицы, в том числе толщина двойного слоя и его физические свойства. Получены соотношения, связывающие поверхностный и электрокинетический потенциалы частицы, а также соотношение для электрокинетиче-ского радиуса частицы, выраженное в долях дебаевского радиуса экранирования и соответственно концентрации электролита.