Границы применимости корректирующего кольца в аподизаторе с круглой зубчатой диафрагмой

Данная работа является продолжением цикла теоретических исследований свойств аподизатора с круглой зубчатой диафрагмой (ЗД) и узким корректирующим кольцом (КК) внутри ЗД [1–3]. Оптическая схема такого аподизатора состоит из ЗД и пространственного фильтра (ПФ) в виде телескопа Кеплера с ограничивающей диафрагмой (ОД) в общем фокусе объектива и окуляра, где ЗД по сравнению с круглой диафрагмой одновременно сглаживает плато и формирует профиль крыльев пучка. Роль непрозрачного КК, расположенного вблизи зубцов диафрагмы, состоит в дополнительной коррекции профиля пучка на выходе аподизатора из ЗД и ПФ. Такая коррекция впервые предложена в патенте [4]. При правильно выбранных параметрах кольца и аподизатора она позволяет заметно уменьшить искажения профиля пучка при его распространении за ПФ.

В [1, 4] обоснована целесообразность применения данной схемы аподизатора в гибридных фемтосекундных лазерных системах видимого диапазона, в которых фемтосекундный импульс формируется в твердотельном задающем генераторе, а затем усиливается в газовой среде на переходе С-А эксимера XeF (~480 нм) [5–9]. Особенностью указанного усилителя является сравнительно низкий коэффициент усиления ~ 2^10 –3 см –1, что приводит к необходимости применения многопроходных оптических систем. Характерная величина диаметра пучка в усилителе [5] составляет 2 см, а общая длина оптического пути в активной среде может достигать 40 метров. Это со- ответствует числу Френеля ≈ 2. При такой длине трассы становятся важными дифракционные искажения пучка, в сильной степени зависящие от профиля пучка на входе в усилитель. Рассматриваемый аподизатор позволяет сформировать пучок, поперечный профиль которого имеет почти плоскую вершину и плавный переход от плато к резко спадающим крыльям. Применение такого аподизатора в качестве согласующего элемента между задающим генератором и усилителем позволяет повысить эффективность использования энергии, запасенной в активной среде усилителя, в том числе и вследствие уменьшения дифракционных искажений пучка при распространении в усилителе.

Альтернативные методы аподизации, обзор которых представлен, например, в [10], не соответствуют целевому применению исследуемого аподизатора.

Теоретическая модель аподизатора цилиндрической геометрии, состоящего из ЗД и ПФ, построена в [1, 2]. В [3] показана возможность улучшения с помощью КК в [4] профиля выходного пучка в таком аподизаторе. В настоящей работе исследованы границы применимости метода КК-коррекции.

Все расчеты делались с помощью программы Wolfram Mathematica.

1.    Теоретическая модель

На рис. 1 показана взятая из [3] схема аподизатора, образованного ПФ с ОД и круглой ЗД на входе с КК внутри нее. В расчетной модели [1, 2] предполагалось, что ЗД, КК и входная (бесконечно тонкая) линза находятся в одной входной плоскости и что на вход аподизатора приходит монохроматическое поле с плоским фазовым фронтом и радиальной симметрией амплитуды.

Поле на выходе аподизатора получено в [1, 3] в интегральном виде (без КК – в [1, 2]; с КК – в [3]) из двух последовательных решений параболического уравнения (ПУ) в цилиндрической системе координат: от входа ПФ до ОД (этап 1 [1, 3]) и от ОД до выхода ПФ (этап 2 [2, 3]). Диаметр ОД выбирался таким, чтобы за счет обрезания зубчатых компонент структуры поля, образующегося при фокусировке прошедшего через ЗД излучения, на выходе ПФ формировалось поле с той же радиальной симметрией амплитуды, какая задана на входе аподизатора.

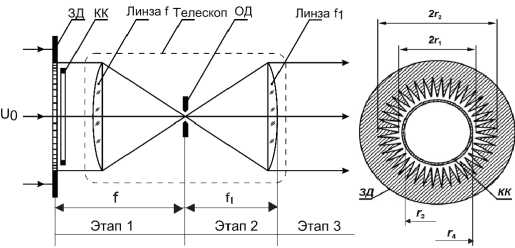
Рис. 1. Схема аподизатора из ЗД и ПФ на базе телескопа Кеплера с ОД в общем фокусе объектива и окуляра. Справа показана ЗД с торца ПФ с дополнительным КК внутри

В данной работе расчеты делались для однородного падающего поля амплитуды U 0 . Обобщение на случай Гауссова пучка с плоским фронтом (перетяжка) принципиально не меняет анализа [1 –3]. Запишем решение на выходе ПФ в безразмерном виде:

U ( x ) = - U ( R , f + f l ) / ( U 0 f / f . ),                (1)

где размерное поле U(R, f + f1) нормировано на поле U0 f / f1 в приближении геометрической оптики (ГО), а размерная поперечная координата R нормирована на ширину пучка a = r1 f1 / f в приближении ГО x = Rf / r f, = R / a. (2)

Для ЗД-ПФ без КК поле (1) определено тремя независимыми безразмерными параметрами аподизатора:

Ъ        2ⁿP o r i _ ^{X f 2 ( f -1} + ^{f -1} )

D = r / ^Ц 1 = Xf ; '       4n r?

В (1 –3) f, f1 – фокусы линз ПФ (соответственно, f + f1 – продольное расстояние от ЗД до выхода ПФ), r1 и r2 – внутренний и внешний радиусы ЗД с четным числом N симметричных зубцов треугольной формы, p0 - радиус ОД, X - длина волны излучения, А - фаза в интегральном решении ПУ. Параметр D в (3) – характеристика ЗД, Ц1 - характеристика ОД (задается po), а фаза А возникает из-за использования в обоих решениях ПУ приближения Френеля, а не Фраунгофера, что обусловлено оптической схемой ПФ. Предположение о треугольных зубцах в ЗД не меняет общности анализа, поскольку в [2] показано, что определяемый формой зубцов профиль крыла пучка (1) с хорошей точностью зависит лишь от нулевого и второго моментов формы зубца (результат свертки в решении ПУ формы зубца с нулевой функцией Бесселя). Поэтому без потери точности решения не треугольные зубцы ЗД можно заменить на эквивалентные треугольные с другим значением D.

Решение (1) в [1–2] не зависит от числа зубцов N при условии, что ц 1 < (0,9 ^ -8,5)/ D . Для диапазонов параметров ц 1 и D , рассмотренных в данной работе, минимальное N находится в интервале от 30 до 80.

При выбранной нормировке осей пучок U ( x ) имеет характерный сплюснутый вид и получается примерно единичного радиуса и с единичной амплитудой плато. Так как профиль U ( x ) радиально-симметричен, мы далее будем рассматривать только его половину. В окрестности x = 1 плато переходит в крыло, которое при x > 1 для D >  1,3 определяется лишь D и хорошо описывается функцией ( D – x )/( D – 1) x , поскольку в цилиндрической геометрии ЗД-ПФ форма крыла пучка выражается функцией F ( x )/ x , где F ( x ) =( D – x )/( D – 1) – профиль треугольного зубца [2].

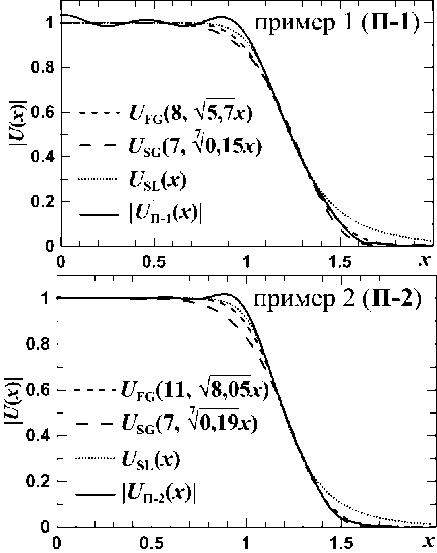
На рис. 2 показаны два профиля | U ( x ) | в аподизаторе без КК, которые сопоставлены с тремя профилями известных аналитических слабо дифрагирующих пучков [11] (штриховые и пунктирные кривые).

а)

б)

Рис. 2. Сравнение / U(x) / на выходе аподизатора без КК при Ц 1 = 15; D = 1,6; А = 0,003 ( П-1 ) и при Ц 1 = 20; D = 1,5;

А = 0,003 ( П- 2 ) - сплошные кривые (численный расчет), с моделями FG и SG-пучков (штриховые кривые).

Пунктир – модели SL-пучков (близкие FD-пучкам)

При сравнении | U ( x ) | с разными аналитическими пучками [11–13] было установлено, что профиль | U ( x ) | лучше всего описывается двумя функциями из обзора [11]: FG (сплюснутый Гаусс – flattened

Gaussian) и SG (супер-Гаусс), которые далее и анализируются. Два других типа пучков, рассмотренных в [11], – SL (супер-лоренц) и FD (пучок Ферми– Дирака) мы исключили из детального анализа, т.к. их длинные хвосты (рис. 2) не соответствуют профилям (1) и увеличивают деформацию пучка за ПФ. В [3] сравнение было проведено только с FG-пучками.

Формулы для FG- и SG-пучков у нас отличаются от выражений в [11], поскольку относятся к амплитудам, а не интенсивностям, и используется другая нормировка по осям: по оси ординат в центре амплитуда равна единице, а по оси абсцисс безразмерная координата р с помощью параметра p переводится в x из (2). В формулах еще присутствует целочисленный параметр n, определяющий крутизну крыла n ρ2k

Ufg ( П, р ) = exp (-р 2 )^   , р = ppX, к=0 k!

U SG ( П , Р ) = exp ( - Р n ) , Р = V px .

Числа p и n подбирались подгонкой под форму крыла | U ( x ) | , которая зависит от D ; поэтому подобранные профили одинаковы для | U ( x ) | при разных p i и А . На рис. 2 показаны (4), (5), подобранные для D =1,6 и D =1,5, которые сравниваются с | U ( x ) | при Ц 1 = 15; D =1,6; А = 0,003 - пример 1 ( П-1 ) и при p i = 20; D =1,5; А = 0,003 - пример 2 ( П-2 ). Почему взяты именно эти примеры, будет объяснено ниже. Рассмотрим мы далее и случай А = 0. На рис. 2 для сравнения приведены и SL-пучки, близкие FD-пучкам, с длинными хвостами, которых нет у | U ( x ) | .

Имеются 3 отличия | U ( x ) | от FG/SG-пучков: амплитудно-фазовые наросты в окрестности x = 1, слабые колебания амплитуды и фазы на плато и обычно в разы больший размах этих колебаний (выброс) в центре пучка. Подчеркнем, что на краю плато, где у | U ( x ) | всегда выступ, у FG/SG-пучков амплитуда монотонно уменьшается.

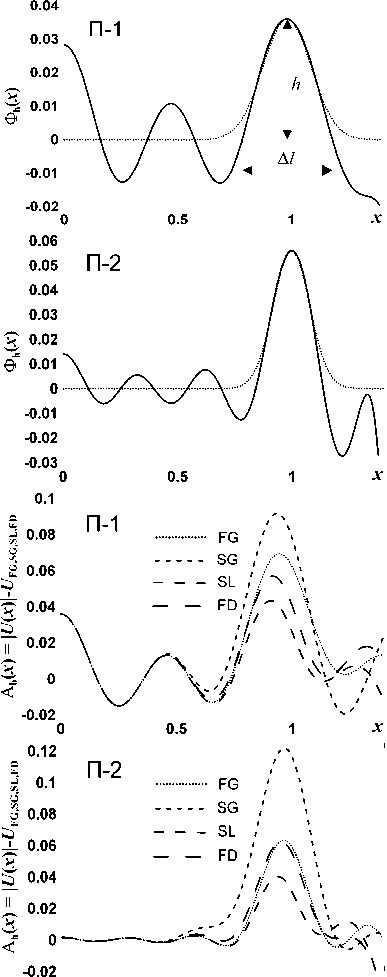
Амплитудные отличия видны на рис. 2, а на рис. 3 они показаны в явном виде вместе с фазами U ( x ).

Определим неровность плато поля глубиной модуляции интенсивности (ГМ), понимая под ней удвоенную разницу максимума и минимума амплитуды на плато (отнесенную к единичному уровню на плато).

Амплитудным наростом Ah назовем разность | U (x) | и пучка (4) или (5). Он состоит из остаточных колебаний профиля с выбросом в центре (крылья Ah) и разности в окрестности x = 1 (основной максимум Ah). Бόльшую часть максимума Ah составляет разность | U(x) | и (4), (5) на краю плато, которая в основном определена D. А выступ над плато там же у | U (x) | – лишь небольшая часть максимума Ah. Этот выступ слабо зависит от p и D, сильнее от А - с ее увеличением он растет и сдвигается к центру пучка [3]. В итоге Ah зависит в основном от D, слабо уменьшается с ростом p и немного увеличивается с ростом А. Различие Ah относительно разных функций из [11] есть разность этих функций в окрестности x = 1 (рис. 3в, г), т.е. в основном максимуме Ah.

а)

б)

в)

о

0.5

X

Рис. 3. Ф (сплошные линии) и A h с рис. 2 (штриховые линии на графиках (а) и (б)). Пунктир на графиках (а) б) – модель гауссоиды основного максимума. На (а) показано определение

г)

ширины A l и высоты h основного максимума нароста

При А ^ 0 надо учитывать еще и фазовые наросты Ф h (не зависят от модели [11], в отличие от A h , совпадая с фазой U ( x )). На рис. 3 фазовые и амплитудные наросты показаны для П – 1,2 . У П –2 наклон крыла круче ( D меньше) и более гладкое плато ( р больше), поэтому у A h в П –2 почти нет крыльев.

Расчеты показали, что основное искажение профиля пучка (1) при его распространении за ПФ по сравнению с FG- и SG-пучками происходит от амплитудного нароста (роль фазового мала) и от выбро- са амплитуды в центре пучка. Для сохранения достаточно гладкого профиля у пучка на интересующих нас расстояниях, отвечающих NF ® 5^2, у U(x) надо ограничить колебания амплитуды на плато величиной ГМ≤ 10% и скомпенсировать амплитудный нарост.

Ограничение колебания амплитуды на плато (включая выброс в центре пучка) достигается ограничением диапазона параметров (3) [2, 3]: ц 1 >10, А< 0,005; D > 1,4 при щ ® 11 + 12 с плавным переходом к D >  1,1 при щ >  40. Увеличение щ при данном D уменьшает колебания на плато и выброс в центре. Параметр ц 1 , как упоминалось выше, ограничен еще и сверху числом зубцов ЗД для восстановления радиальной симметрии U ( x ). Ограничение на щ сверху для эффективности КК далее окажется у нас более сильным. Параметр D тоже может быть ограничен сверху, например, допустимым наклоном крыльев.

Предложенная в патенте [4] корректировка амплитудного и частично фазового наростов у U ( x ) с помощью КК теоретически исследована и обоснована для условий патентного предложения в [3]. При добавлении к ЗД-ПФ тонкого непрозрачного КК (рис. 1) с безразмерными радиусами р ₃ , ₄ (или с безразмерным радиусом центра КК и его шириной)

, „ П з + П 4            _

П з,4 = Г з,4 / Г й П 0 =--- 2---; ^ЛП = П 4 - П з

к U ( x ) добавляется поправка, зависящая от (6), щ и А , которую, как в [3], обозначим Y ( x ). Она позволяет частично скомпенсировать наросты на краю плато.

Из известного интегрального решения радиальносимметричного ПУ для поля, нормированного как (1), на расстоянии z за ПФ имеем (этап 3, рис. 1)

x ²

2 Z 7                      vL

U ( x , Z ) = -    U ( v ,0J I — I ve 2z d v ,           (7)

^iZ 0 I z )

где U ( x¸ 0)= U ( x ) или U ( x¸ 0)= U ( x )+ Y ( x ); x = r / a – поперечная координата r , нормированная так же, как координата R на выходе ПФ (2); а z̃ – продольная координата z от выхода ПФ, выраженная через число Френеля за ПФ N F = a ² / X z

Z = z X f ² /2п( r 1 f ) ² = 1/ 2n N _F. (8)

За пределами [3] остались вопросы выбора пучка, под который нужно или можно корректировать U ( x ), и зависимость корректировки от неоптимального выбора параметров (3), (6) аподизатора, т.е. границы применимости корректировки [3, 4]. Мы покажем, при каких условиях и в какой степени КК позволяет скомпенсировать нарост профиля у U ( x ) и уменьшить ГМ при распространении скорректированного пучка.

2.    Распространение пучков за ПФ

Для расчетов полей (7) за ПФ в качестве U ( x ) брались аналитические модели поля в виде

U ( x ) = [ U fg,sg,... ( x ) + A h ( x ) ] exp [ i Ф h ( x ) ] ,             (9)

где U FG,SG,… – модельные пучки, подогнанные под U ( x ), A h и Ф _h моделировались из кусков аналитических функций, воспроизводящих всю структуру расчетных наростов до нижней части крыльев (без хвостов U ( x )) или в виде лишь основных максимумов наростов (как на рис. 3 а, б ), или с разными боковыми структурами. Делались расчеты (7) и без одного или обоих наростов в (9) . Любой пучок представим в виде (9), если наросты воспроизведены адекватно.

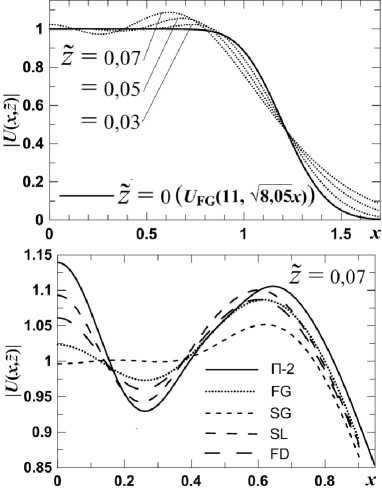
При распространении сплюснутых пучков из-за дифракции формируется заметный максимум на краю плато, еще 2–3 экстремума на половине плато и уменьшается наклон крыла. Этот типичный вид деформации профиля заметно различается для функции (1) и подогнанных под нее функций по размерам деформации на конкретных расстояниях. На рис. 4 а показана трансформация FG-пучка для D = 1,5 (отвечает П –2 ) с ростом z̃ , а на рис. 4 б – пример отличия профилей (7) для всех функций из [11] и профиля для П – 2 , рассчитанного с учетом всей структуры наростов.

а)

б)

Рис. 4. Поперечные профили / u (x,Z) / (7) на расстоянии Z при U (x, 0) = U П – 2 (x) и в виде моделей FG, SG, SL и FD из [11], подобранных для D = 1,5

Видно, что деформации подогнанных под D пучков из [11] с рис. 2 при Z « 0,03^0,08 ( N f ® 5^2) заметно различны. Самый медленно деформируемый – SG-пучок, потом FG, потом близкие SL и FD. Это уже говорит о роли наростов в деформации U ( x,z̃ ), которая не зависит от модели U ( x ): различия в (7) для U FG,SG ,… из (9) возникают из-за вклада наростов.

Более медленная деформация SG-пучка обусловлена его более плавным спадом на краю плато. Коррекция | U(x) | под SG-пучки с помощью КК возможна, но лишь в очень узком диапазоне параметров аподиза- тора, в отличие от коррекции под FG-пучки, что показано далее. Поэтому нет необходимости исследовать пучки с еще более плавным спадом, чем у SG.

Поскольку у пучков FG и SG деформация заметно ниже, чем у пучков (1) с наростами, ГМ пучка за ПФ понизится, если убрать наросты U ( x ) под U FG или U SG .

Расчеты по (7), (9) с разными моделями наростов показали, что для оценки ГМ за ПФ допустимы модели A h , состоящие лишь из основного максимума, т.к. именно он определяет профиль U ( x, z̃ ) и его ГМ, а не боковая структура A h . Отличия от более точных моделей, в основном не меняющие ГМ пучка, видны лишь в выбросах | U (0, z) | , зависящих от zu чувствительных ко всем деталям наростов – точности их приближения, в том числе и на крыльях, учету Ф h , учету хвостов U ( x ).

Роль имеющегося при А^ 0 у U ( x ) нароста фазы Ф h мала по сравнению с A h и тоже проявляется в | U (0, z) | , не меняя ГМ. Тем более мала роль боковой структуры Ф h . Без потерь в точности можно в (9) брать Ф h в виде лишь основного максимума.

В расчетах мы в основном брали в (9) U FG , т.к. рассмотрение (9) с U SG получается простым включением в A h разницы основных максимумов.

Функция U ( x, z̃ ) для U FG представима суммой нескольких гауссоид высшего типа – собственных решений ПУ, и анализ U ( x, z̃ ) под этим углом приводит к интересным выводам (см. Приложение).

3.    Модельные расчеты влияния основных параметров наростов на поле за ПФ

Из (9) поправка от малых наростов к решению U FG ( x , z̃ ) (7) для U ( x , 0) = U FG примерно равна

U(x, z) - Ufg(x, z) ® iUfg(V)Фh(V) +L (vx) iv2 .          (10)

J₀ 1      I ve ^{2 z} d v ,

+ A h ( v )          J ( z J

i

'^

e2z iz ^

iz ₀

где первое слагаемое в квадратной скобке как минимум в 1,5 раза меньше второго (см. рис. 3). Т.к. у U _fg( x , z ) при z ® 0,03-0,08 мала мнимая компонента (см. (П8) в Приложении), вклад наростов в | U ( x , z ) | определяется слагаемым A h в (10). Поэтому проследим за A h ( x , z̃ ) – эволюцией A h из (10).

Эволюция разных A h происходит похоже: максимум расползается, уменьшаясь, и формируется экстремум при x =0, который растет, превышая максимум A h . Что и проявляется в | U ( x , z ) | (рис. 4). Различие картин для разных A h – в расстояниях по z̃ описанных стадий и в абсолютных размерах. На рис. 5 показан процесс для двух A h . Главное отличие взятых A h – в ширине максимума, что сильно влияет на зависимость от z̃ стадий деформации. В Приложении дано качественное объяснение эволюции A h на рис. 5.

Расчеты показали, что определяющими по влиянию на деформацию | U(x, z) ] и ее ГМ параметрами являются ширина Аl, высота h и положение вершины основного максимума Ah и именно в такой последовательности. Поэтому мы исследовали на простых моделях Ah и Фh (рис. 3) влияние на ГМ за ПФ этих параметров наростов, а затем рассчитали (7) с близкими реальности Ah и Фh для ключевых примеров.

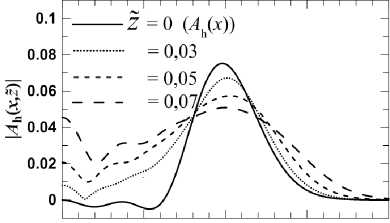
а)

б)

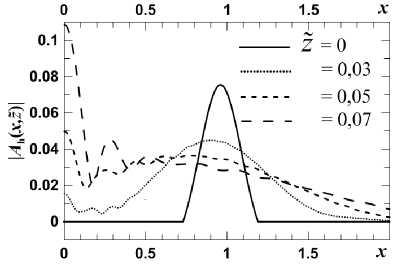
Рис. 5. A h (x,z̃) – эволюция A h на расстоянии z̃

Влияние основных параметров наростов на ГМ пучка при z « 0,03-0,08 было изучено для П -1,2 с U _FG в (9): вершины наростов заметно смещались, а А l и h менялись в 1,5–3,5 раза в обе стороны. В эксперименте такие вариации могут возникать из-за неполной компенсации наростов с помощью КК.

Роль высоты A h из (10) очевидна – деформация пучка пропорциональна высоте. При неоптимальной компенсации A h максимум можно скомпенсировать частично по высоте или ширине, что меняет ширину и центр остаточного максимума. Сужение максимума уменьшает у | U ( x , z) | максимум на краю плато, сдвиг мало влияет на максимум. Но и сужение, и сдвиг к центру увеличивают модуляции на плато и выброс при x =0 в зависимости от z̃ .

Для оценки влияния параметров Ф _h на | U ( x , z) | они тоже менялись в разы. Для z « 0,03 - 0,08 при этом максимум на краю плато почти не менялся, а модуляция плато и выбросы в центре были заметно слабее, чем при вариациях A h , даже при сильном завышении вариаций Ф h по сравнению с имеющейся фазой. КК обычно несколько уменьшает Ф h (см. далее рис. 8 б ).

4.    Эффективность КК в компенсации амплитудного нароста пучка на выходе ПФ

Итак, для понижения ГМ у U (x, z̃) на расстояниях, отвечающих NF®5-2 за ПФ, надо скорректировать форму | U(x) | на выходе ЗД-ПФ, подогнав ее под FG-, а еще лучше под SG-пучок. Для этого надо уменьшить выброс амплитуды в центре плато, ограничивая параметры (3), и убрать основной максимум Ah.

Если желательно получить ГМ на плато U ( x , z̃ ) в 10% при z̃ ≈ 0,03 ÷ 0,08 (как в [3]), то из рис. 6 видно, что даже для FG- и SG-пучков лишь SG-пучки при D ≥ 1,5 приемлемо удовлетворяют такому критерию на этих z̃ . Несколько хуже FG-пучок при D ≥ 1,6. Для D <  1,5, даже если КК скорректирует U ( x ) под FG-или SG-пучки, заметно понизить ГМ не удастся. Это накладывает на D более жесткое условие, чем приведенное выше ограничение гладкости плато на выходе ПФ – D ≥ 1,5 при любых µ 1 .

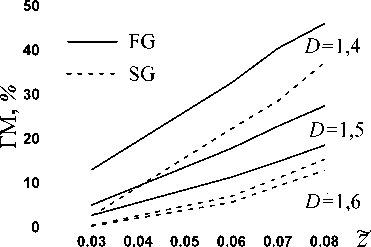
Рис. 6. ГМ (7) в виде кусочно-линейных функций, соединяющих расчеты при z̃ = 0,03; 0,06; 0,07 и 0,08, для U fg, sg , отвечающих указанным D. Параметры (4) и (5) при D = 1,6 и D = 1,5 приведены на рис. 2; для D = 1,4 они равны:

UFG(20, 15x) и USG(9, 9 0,17x)

Простой способ убрать A h у U ( x ) – поместить непрозрачное корректирующее кольцо-экран (КК) во входную апертуру ПФ в область, отвечающую максимуму A h в приближении ГО. Для эффективного выполнения задачи формы и параметры максимумов A h ( x ) и поправки Y ( x ) от КК должны совпасть, что зависит от параметров (3) и (6). Здесь есть трудность.

У максимума A h выпуклая форма (рис. 3), которая в основном зависит от D и слабо – от µ 1 и ∆ . При ∆≤ 0,001 его ширина ∆ l и высота h слегка зависят от µ 1 , при бόльших ∆ зависимость почти пропадает, сохранясь лишь при малых µ 1 . Это верно при всех D ≈ 1,4÷ 1,6 и ∆≤ 0,005. C ростом µ 1 уменьшается боковая структура A h (плато сглаживается).

У поправки Y (зависящей от ∆, µ1 и (6)), как показано в [3], при ∆ =0 (когда U (x) и Y (x) действительны) форма тоже выпуклая, сохраняющая подобие: высота максимума h прямо, а ширина ∆l обратно пропорциональны µ1 (см. (11)). То есть с ростом µ1 ∆l у Y резко уменьшается, а относительный размер боковых экстремумов сохраняется. При ∆ > 0 зависимость ∆l от µ1 слабеет с ростом ∆, но все-таки заметна. Также сохраняется относительный размер боковых экстремумов, которые с ростом µ1 и ∆ могут даже исказить выпуклый вид основного максимума, срастаясь с ним. От ∆ же зависимость h и ∆l у Y существенна. Поэтому подогнать ∆l у Y и Ah при каждом ∆ если можно, то лишь при определенных, малых µ1, как видно из рис. 7. Параметры КК на ∆l у Y не влияют [3]: ∆η определяет h, а η0 – положение основного максимума Y. Значит, для эффективности КК ЗД-ПФ надо согласовать с КК по ∆l выбором µ1, который зависит от ∆. Несогласование Ah и Y (даже выпуклой формы) проявляется в компенсации с помощью Y лишь части Ah – по ширине или по высоте.

а)

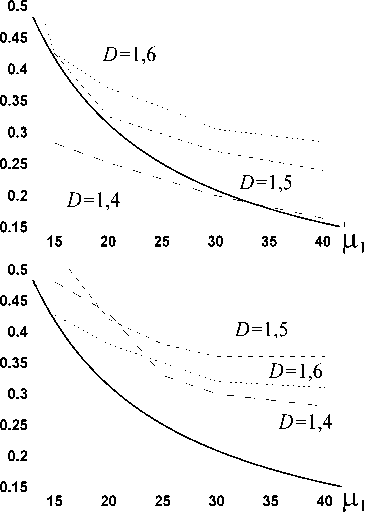
б)

Рис. 7. Функции ∆ l (µ 1 ) при ∆ = 0. Сплошные линии – (11) для максимумов Y, штриховые – расчет для A h при разных D (а – относительно FG-пучка, б – относительно SG)

Согласование ∆ l для поправки Y с A h при ∆ =0 показано на рис. 7. Сплошные линии – это зависимость

∆ l ( µ 1 ) ≈ 6,27 µ 1

для поправки Y , полученная в [3], штриховые линии – ∆ l (µ 1 ) для A h . Видно, что обе ∆ l согласуются для D = 1,6 под FG / SG-пучки при µ 1 ≈ 15; для D = 1,5 и D = 1,4 – под FG-пучки при µ 1 ≈ 15÷20 и µ 1 ≈ 30÷35 соответственно. Аналогична ситуация для D ≈ 1,5÷ 1,6 и при ∆ = 0,003 [3]. Для D = 1,4 при ∆ = 0,003 согласования нет ни под FG-, ни под SG-пучки.

При ∆ ≠ 0 Y ( x ), как и U ( x ), комплексна с, вообще говоря, немалой мнимой частью. Тогда Y надо добавить в (9), а Im Y и Re Y – почленно в (10). Из (10) видно, что Im Y в основном влияет на Φ h , а согласование Y с A h представляет неопределенность: приемлемый разброс ∆ l и h у Y можно оценить из двух графиков – в виде | Y | и Re Y . При выпуклых формах основного максимума ∆ l одинакова по обеим оценкам. А h, определяющая ∆η для КК [3], через Re Y несколько меньше, чем через | Y | , что дает интервал для подбора ∆η .

Таким образом, скорректировать U ( x ) под FG- или SG-пучок с помощью КК можно лишь выбором нужных µ 1 у ПФ. Взятые выше П –1,2 для ПФ-ЗД соответствуют примерам такого выбора µ 1 при ∆ = 0,003 для D = 1,6 и D = 1,5.

Даже при ∆ =0, когда (11) связывает ∆ l у Y с µ 1 , не удается выразить формулой зависимость ∆ l у A h от µ 1 и D . Как видно из рис. 7, ∆ l у Y и A h согласуются при малых µ 1 , когда ∆ l у A h еще зависят от µ 1 . Поэтому подбор µ 1 делается графически, как на рис.7. Тем более это так, когда ∆ ≠ 0 и обе ∆ l (у A h и Y ) еще и заметно зависят от ∆ . Приведенные выше оценки µ 1 для 1,4 ≤ D ≤ 1,6 и ∆ ≤ 0,003, как показано далее, позволяют хорошо скорректировать пучки с помощью КК.

Для наших целей не важно, при каких µ 1 и ∆ с данным D корректировать U ( x ) на выходе ПФ. Но это важно для возможности использовать для этого метод КК. Также может иметь значение то, что коррекция не дает точный FG- или SG-пучок. Даже если параметры ПФ-ЗД-КК подобраны оптимально, у профиля пучка остаются какие-то мелкие «дефекты» – волны на плато, фазовая добавка или неточности среза A h . А тем более, если какие-то параметры ПФ-ЗД-КК не оптимальны. Далее на конкретных примерах мы покажем, как это скажется на ГМ полученных пучков на расстояниях за ПФ, отвечающих N F ≈ 5÷2.

5.    Примеры корректировки пучков с помощью КК

Учитывая диапазон µ 1 для согласования ∆ l у A h и Y для разных D и ∆ ≤ 0,003 (рис. 7 и [3]), мы рассчитали с помощью (7) и (9) конкретные примеры.

Для D = 1,6 (согласованное µ 1 ≈ 14÷ 15 под FG- и SG-пучки) мы рассчитали при ∆ =0 согласованный по параметрам (6) КК пример с µ 1 = 15, а при ∆ = 0,003 – пример из [3, 4] с µ 1 = 14 – пример 3 (П –3), который близок П –1 . П –3 разобран в [3] под FG-пучок при неоптимальном выборе параметров КК (отвечающих данным патента [4]). Здесь мы рассчитали корректировку П –3 под FG- и SG-пучки при оптимальных параметрах КК, а также при неоптимальных значениях µ 1 >  15, т.е. несогласовании по ∆ l .

Для D = 1,5 (согласованное µ 1 ≈ 15÷20 лишь под FG-пучки) мы рассчитали при оптимальных µ 1 подбор КК при ∆ =0 и для П –2 при ∆ = 0,003.

Для D = 1,4 КК может скорректировать U ( x ) под U FG лишь при ∆≤ 0,001. При ∆ = 0,001 оптимальное µ 1 ≈ 25, а при ∆ =0 – µ 1 ≈ 30÷35. Из рис. 6 видно, что ни у U FG , ни у U SG не будет малых ГМ при z̃ ≈ 0,06 ÷ 0,08, однако скорректировать с КК U ( x ) под U FG можно. Мы рассчитали выбор КК для U ( x ) при ∆ =0 и µ 1 =30.

В расчетах (7) для (9) брались модели наростов, воспроизводящие всю их структуру.

• 5.1.    Корректировка пучка при D = 1,6

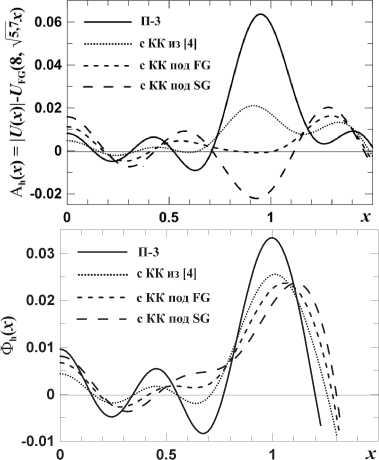
Корректировка U (x) при оптимальных параметрах ЗД-ПФ-КК (совпадение ∆l у основных максимумов Y и Ah подбором µ1, h подбором ∆η, и совмещение их вершин выбором η0 [3]) приводит к получению на выходе ПФ пучка, приближенного к FG или SG и также слабо дифрагирующего за ПФ, как и сами FG/SG-пучки. Это видно на рис. 8,9, где, соответ- ственно, показано, как меняются Ah и Φh в П –3 и меняется ГМ пучков за ПФ в П –3 и при ∆ =0.

а)

б)

Рис. 8. Амплитудные и фазовые наросты U(x) относительно U FG для П – 3 (без КК) и с различными КК

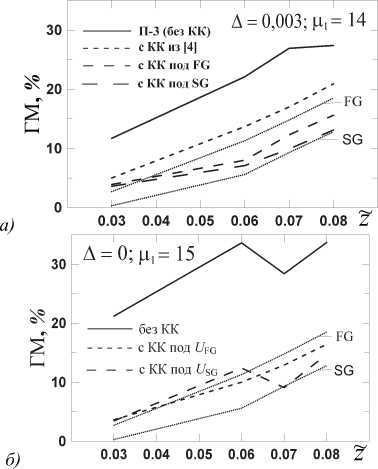
Рис. 9. ГМ U(x, z̃), рассчитанные как на рис. 6. D = 1,6.

Пунктирные линии взяты для U FG, SG с рис. 6

Выбор параметров КК ( η 0 ; ∆η ) в П –3 на рис. 8, 9 соответствует неоптимальным (0,965; 0,01) под U FG из [4] (пример разобран в [3]) и оптимальным (0,95; 0,015) под U FG и (0,94; 0,02) под U SG . При ∆ =0 и µ 1 = 15 оптимальные параметры КК под U FG – (0,945;0,0154), под U SG –(0,935; 0,02).

Из рис. 8 видно, что при оптимальном подборе параметров КК под FG максимум A h практически убирается. Остаточный нарост под SG на рисунке отрицателен, т.к. он тоже показан относительно FG-пучка (т.е. в него включена разность U FG и U SG в (9)); показанный под SG он тоже будет нулевым.

КК также немного уменьшает и фазовый нарост.

А из рис. 9 а видно, что все КК с рис. 8 заметно понижают ГМ за ПФ. Т.е. неоптимальный выбор КК не сильно сказывается на качестве полученного пучка. При подборе КК под SG ГМ немного выше, чем у SG, а под FG – даже немного ниже, чем у FG. Расчеты показали, что в основном это вклад остаточной фазы.

Неоптимальный выбор ц 1 сказывается на качестве пучка сильнее. Для П –3 мы подобрали КК для ц 1 >  15- ц = 20; 25; 40. В отсутствие КК A h близки при разных ц 1 ; близки и ГМ пучков за ПФ. С ростом ц поправка Y становится ýже A h . Два проявления несогласования ЗД-ПФ с КК (частичный срез максимума A h и то, что с ростом щ у У боковая структура не уменьшается, как у A h ) порождают рост колебаний на плато I U ( x ) | , что портит достигнутую с помощью ЗД гладкость плато, хотя A h частично убирается. Колебания на плато (в разумных пределах при небольшом выбросе в центре) влияют на рост ГМ за ПФ слабее основного максимума A h . Поэтому частичный срез A h при росте колебаний на плато в каких-то границах снижает ГМ за ПФ. При ц 1 = 20 ГМ с КК снижается на z ® 0,03-0,08 более чем вдвое и оказывается немногим выше, чем у FG-пучка, а при ц > 25 уже нет. В этом случае ситуация одинаково плоха, убираем ли A h частично по высоте или частично по ширине. При ц 1 =40, например, от максимума A h можно убрать лишь узкие куски и плато портится (см. рис. 6 в [3]), что совсем не снижает ГМ за ПФ за счет КК.

• 5.2.    Корректировка пучка при D = 1,5

• 5.3.    Корректировка пучка при D = 1,4

Из рис. 6 видно, что срез наростов под U FG при D = 1,5 весьма желателен. ЗД-ПФ и КК согласованы здесь при щ ® 15-20 под FG-пучок и для А = 0, и для А = 0,003. Мы рассчитали подбор КК для П -2 и при А = 0 для щ = 15; 20. В трех рассмотренных случаях получилось, что оптимально подобранные КК хорошо подгоняют I U ( x ) I под U FG , понижая ГМ за ПФ почти до качества FG-пучка.

Попытка подогнать U ( x ) под U SG дает результат хуже подгонки под U FG . Это связано с тем, что под SG-пучок A h намного шире (рис. 3 г ) и КК убирает либо только макушку A h (что фактически означает срез под FG), либо сужает A h со сдвигом к центру, почти не уменьшая высоты, что увеличивает ГМ при z ® 0,03-0,08, порождая глубокий провал или выброс в центре пучка (это иллюстрирует рис. 5 б ).

Корректировка с А = 0 при ц 1 = 15; 20 показала, что, подгоняя | U ( x ) | под один и тот же FG-пучок, мы получаем различную структуру остаточных колебаний на плато у пучков. При щ = 15 у | U ( x ) | без КК были заметные колебания на плато (ГМ ® 10%), КК их сгладило до ® 3 %. А при ц 1 =20 КК почти не изменило эти колебания - они были и остались ® 6 %. А ГМ пучков за ПФ оказались одинаковыми. Т.е. остаточные колебания на плато мало влияют на дифракцию пучка; задача поправки Y – убрать основной максимум A h , а не уменьшать остаточные колебания.

Расчеты показали, что для D = 1,4 КК может скорректировать U ( x ) лишь под FG-пучок и лишь для А< 0,001 при ц ® 30-35 ([3], рис. 7). И хотя даже у FG-пучков ГМ не малы при z ® 0,06-0,08 (см. рис. 6), качество FG-пучка из U ( x ) получить можно. Мы рассчитали для А = 0 и ц 1 = 30 ГМ на расстояниях z ® 0,03-0,08 как для пучка без корректировки, так и с оптимальным КК. ГМ последнего оказалась близка ГМ FG-пучка на z ® 0,03-0,08 - примерно на 5 % меньше ГМ исходного пучка.

Заключение

Проведено сравнение профиля пучка U ( x ), аподи-зированного пространственным фильтром с зубчатой диафрагмой на входе, с профилями слабо дифрагирующих сплюснутых аналитических пучков. Показано, что отличия от них в U ( x ), главное из которых – амплитудный нарост на краю плато, заметно увеличивают глубину модуляции плато пучка за ПФ. Чем более плавен край плато на выходе ПФ, тем ниже будут ГМ за ПФ. Поэтому для уменьшения ГМ на расстояниях N F ® 5-2 надо у U ( x ) убрать амплитудный нарост. Предложенный в патенте [4] метод сглаживания края плато за счет добавления внутрь ЗД непрозрачного корректирующего кольца в область прообраза нароста в приближении геометрической оптики, позволяет скорректировать профиль U ( x ) на выходе ПФ под пучки в виде сплюснутого Гаусса (FG) или супер-Гаусса (SG).

Корректировка U ( x ) с помощью КК оптимальна при совпадении ширин основных максимумов амплитудного нароста A h и поправки от КК выбором параметра ПФ ц (т.е. радиуса ограничивающей диафрагмы в фокусе ПФ), при совпадении их высот выбором ширины КК Ар , и совмещении их вершин выбором центра КК р ₀ [3], т.е. достигается правильно выбранными параметрами кольца и аподизатора.

В данной работе изучены границы применимости корректировки [4] и ее качество по параметрам ЗД-ПФ. Т.к. в основном корректировка зависит от согласования ширины A h и Y , определяемого параметрами ц 1 и А , она достижима в ограниченной области ц и А .

При А< 0,003 для D =1,6 ЗД-ПФ и КК могут быть согласованы для корректировки под FG- и SG-пучки при ц ® 14-15, а для D =1,5 - лишь под FG-пучки при щ ® 14-20. Для D =1,4 согласование возможно при А< 0,001 лишь под FG-пучки при щ ® 25-35, но заметно уменьшить ГМ пучка при z ® 0,03-0,08 в этом случае уже не удастся .

В итоге при D е1,4 - 1,6 возможна корректировка под FG-пучки при ц1 ® 14-35. Для ц1 ® 14-15 КК позволяют подогнать U (x) под еще медленнее деформируемый SG-пучок, что невозможно при бόль-ших ц1. Тем более КК не корректирует U(x) под пучки с еще более плавным переходом от плато к крыль- ям. То есть корректировку [4] не следует рассматривать как поправку КК для произвольного аподизатора ЗД-ПФ, а надо выбирать параметры всей системы ЗД-ПФ-КК. При согласовании системы по ц1 подбор параметров КК (п0; Ар) повышает качество корректировки U (x), но неоптимальность их выбора сказывается на понижении ГМ слабее несогласования по ц1.

Если корректировка с помощью КК возможна при заданном параметре А , то она возможна и при меньших А , т.к. от А слабо зависит амплитудный нарост, а влияние сопутствующего при А> 0 фазового нароста на ГМ незначительно.

Проведенный анализ показал, когда и как с помощью КК можно на выходе ЗД-ПФ приблизиться к профилям FG/SG-пучков при D ® 1,4 + 1,6, достигнув и их ГМ за ПФ при N _F ® 5-2.