Гранулометрический состав отвальных массивов разрезов Кузбасса

Мониторинг гранулометрического состава отвалов вскрышных пород на действующих разрезах имеет важное значение, поскольку именно он во многом определяет несущую способность отвальных массивов. Это влияние выражается в неравномерном распределении кусков горных пород с различными размерами по высоте. Вместе с тем размеры кусков взорванных пород имеют прямую корреляцию с прочностью пород в массиве [1]. Данные гранулометрического состава взорванных вскрышных пород применяются при математическом моделировании отвалов для геомеханических расчетов их устойчивости.

Актуальность работы также обусловлена тем, что в настоящее время уделяется очень мало внимания исследованиям, направленным на изучение параметров забойных блоков гидравлических экскаваторов. В связи с тем что фирмы-производители предоставляют данные, описывающие параметры черпания экскаваторов, только по усредненным графикам, невозможно сделать вывод об устойчивости экскаватора, расположенного на верхней площадке уступа, при его работе нижним черпанием [2–4]. Угол откоса уступа в этом случае должен рассчитываться индивидуально для каждого из вариантов горно-геологических условий, которых может быть множество из-за разнообразия литотипов разрабатываемых горных пород. Кроме того, надо учитывать связность пород, их ку-сковатость и другие физико-технические свойства.

Помимо решения задач устойчивости массива взорванной горной массы, определенный интерес вызывает оценка использования разрушенных горных пород в качестве наполнителя для очистных со- оружений шахтных и карьерных сточных вод. Влияние гранулометрического и петрографического состава горной массы на фильтровальные характеристики искусственных фильтрующих массивов показано в работах [5, 6]. Изучение гранулометрического состава взорванных пород позволит определить первоочередные подходы к решению вышеуказанных задач.

Материалы и методы

Изучение гранулометрического состава отвального массива имеет своим объектом отдельные куски породы с различными формой и размерами, а предметом – размеры кусков, по которым производится разделение на фракции взорванной горной массы [7]. В гранулометрии геоматериалов форма кусков породы имеет не меньшее значение, чем их размер, поскольку выступает своего рода «определителем» размера.

Интегрально размер и форма куска породы могут быть выражены через среднюю длину секущих, т.е. среднее расстояние между случайными парами точек, принадлежащих поверхности куска:

V average S

где V , S – объем и площадь поверхности куска породы соответственно.

Из-за неизометричности кусков породы их средний линейный размер можно принять за 1,5laverage. Для изометричных тел средний линейный размер совпадает с их истинными размерами (для шара – это диаметр, для куба – ребро). В качестве среднего размера кусков на практике зачастую принимают https://mst.misis.ru/

2021;6(4):259–266

среднее геометрическое или среднее арифметическое максимального и минимального значений линейного размера.

В гранулометрии разрушенных горных пород часто используется понятие эквивалентного диаметра. И для куска породы из развала взорванной горной массы, и для шара, имеющего тот же объем, что и рассматриваемый кусок породы, объем определяется как

V 6 Пlaverage,

где l_average – средний размер куска или его эквивалентный диаметр ( d_eq ).

В плоском случае эквивалентный диаметр куска породы будет равен диаметру круга, площадь которого равна средней площади сечений куска случайными плоскостями.

Вмещающие породы Кузбасса представлены в основном аргиллитами, алевролитами и песчаниками. В значительно меньшей степени встречаются магматические плутонические и метаморфические породы. Замеры длины А, ширины В и толщины С кусков различных размеров для осадочных пород показали соотношение А : В : С = 1 : 0,85 : 0,8 (усредненные значения). Полученное соотношение практически совпадает с аналогичным соотношением для кусков взорванных аргиллитов, алевролитов и песчаников разрезов Кузбасса А : В : С = 1 : 0,8 : 0,75, описанного в работах [8, 9].

В процессе выемки, погрузки, транспортировки и отвалообразования горной массы острые и выступающие ребра кусков породы откалываются, что приближает форму частиц породы к удлинённо-уплощённой.

Для моделирования отвальных (в общем случае – любых насыпных) массивов с применением современного свободно распространяемого (YADE, MercuryDPM и аналогичных) и коммерческого программного обеспечения (PLAXIS, PFC2D, Altair EDEM) формой модельного представления частиц может служить как сфера, так и любая другая объемная фигура с топологически замкнутой поверхностью. Если в начале 2000-х годов последнее было практически невозможно из-за аппаратных ограничений [10, 11], то в настоящее время технически это реализуемо в рамках отдельной лаборатории. Тем не менее моделирование кусков горных пород телами неизометричной формы целесообразно лишь с применением серьезных вычислительных мощностей на современных графических процессорах с распределенной средой моделирования, с применением архитектуры CUDA и PhysX и значительными объемами как графической, так и оперативной памяти, при использовании локальных рабочих станций.

За размер куска породы при моделировании структуры насыпного массива принимается эквивалентный диаметр, вычисленный по данным гранулометрического состава пород, укладываемых в такой массив.

Теоретические основы математического моде- лирования зернистых сред, заложенные отечествен- ными [10–14] и зарубежными авторами [15–18], показывают, что наиболее приемлемой модельной формой частицы зернистой среды является либо одна сфера, либо объемная фигура, представленная сближенными (межцентровое расстояние от 0,2 радиуса) сферами – в объемном или кругами – в плоском случае. Это подтверждается тем, что указанные формы частиц являются наиболее приемлемыми для моделирования сыпучих сред с применением, в частности, свободно распространяемых программных кодов Yade и MercuryDPM, без существенной потери скорости моделирования, в отличие от более сложной формы кусков, состоящих, например, из трех и более сопряженных сфер. Использование сложных форм кусков моделируемой среды приводит к увеличению времени моделирования аналогичного объема среды на один-два порядка даже с применением современных конфигураций персональных компьютеров (твердотельный накопитель формата M.2 с поддержкой NVMe, центральный процессор 4,2 ГГц, оперативная многоканальная память 64 Гб, графический процессор 1,7 ГГц, графическая видеопамять 4 Гб, поддержка CUDA и PhysX).

Изучение текстур насыпных массивов и физико-технических свойств укладываемых пород проводилось как на отвалах Кузбасса, так и в лабораторных условиях [19, 21, 22]. Гранулометрический состав мелкокусковой части отвалов с размерами кусков пород до 50 мм исследовался ситовым методом по ГОСТ 12536–2014, а средне- и крупнокусковой – методом косоугольной фотопланиметрии. При этом при обработке фотографий откосов применялась демоверсия программного обеспечения «Split-Desktop».

Результаты

Результаты исследований гранулометрического состава представлены на рис. 1 и 2. На рис. 2 представлено процентное содержание всех частиц массива (соответствующее кривой 4 на рис. 1).

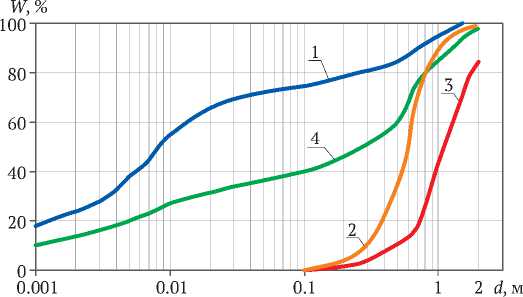
Рис. 1. Интегральные (суммарные) кривые гранулометрического состава отвалов W_I ( _d ) по объемному содержанию фракций: 1 , 2 , 3 – для нижней, средней, верхней частей отвала соответственно; 4 – для всего отвала

Fig. 1. Integral (cumulative) curves of the waste dumps grain size distribution WI(d) by the volumetric content of fractions: 1, 2, 3 – for the lower, middle, upper parts of the waste dump, respectively; 4 – for the whole waste dump https://mst.misis.ru/

2021;6(4):259–266

Из рис. 1 видно, что нижняя треть отвалов содержит преимущественно куски крупных размеров ( d_eq ≈ 0,8 м), средняя часть – средних размеров ( d_eq ≈ 0,4 м), верхняя часть – мелких размеров ( d_eq ≈ 0,04 м). Сегрегация размеров кусков по высоте отвала обусловлена прямой пропорциональностью расстояния перемещения куска по откосу его размеру.

Высокая однородность гранулометрического состава характерна для нижних слоёв отвала (для крупнокусковой массы коэффициент неоднородности C_u = 2,4, для среднекусковой – C_u = 2,2). Значение пористости в нижних слоях достигает значения n = 40 %, а абсолютные размеры пустот – нескольких десятков сантиметров. Нижние слои отвалов характеризуются в целом каркасной или каркасно-незаполненной внутренней текстурой.

Более сложная мелкокусковая система характерна для верхнего слоя отвалов. Текстура этого слоя отличается относительно выдержанной изотропностью из-за резкой разноразмерности частиц ( C_u > 20) и хаотического чередования пространственных решеток различной конфигурации, вплоть до их полного отсутствия. По сравнению с нижней и средней третями отвального массива (по высоте) абсолютные размеры пор верхнего слоя на 1–3 порядка меньше.

Резкое уменьшение пористости и размеров пор обусловлено более интенсивным физическим выветриванием, разрушением кусков и их переупаковкой в верхнем слое с течением времени, по сравнению с нижними слоями. Интенсивность протекания процессов выветривания зависит от водоустойчивости и прочности пород.

Скальные и полускальные вскрышные породы угленасыщенных толщ Кузбасса представлены главным образом аргиллитами, алевролитами и песчаниками различной прочности. Предел прочности на сжатие Rс песчаников (как водонасыщенных, так и сухих) в 1,5 раза выше, чем соответствующий предел прочности аргиллитов и алевролитов. Для отложений Северного и Центрального Кузбасса коэффициент размягчаемости Ks (отношение предела прочности в водонасыщенном состоянии к пределу прочности в сухом состоянии) для песчаников составляет в среднем 0,65; для отложений Южного Куз- басса – 0,7–0,9. Для алевролитов и аргиллитов всех отложений Кузбасса средние значения Ks находятся в пределах 0,5–0,6.

Низкой степенью уплотнения обладают массивы, отсыпанные преимущественно из крепких песчаников. При этом нижние грубообломочные слои отвалов, сложенные кусками с наибольшим пределом прочности на сжатие и наименее подверженные физическому и химическому выветриванию, остаются в течение длительного времени в разрыхленном состоянии. Изменение размеров пор в таких слоях происходит преимущественно за счет постепенного заиливания мелкодисперсной массой, проникающей из верхних слоев.

Для численного моделирования насыпных породных массивов целесообразно перейти от функции F ( d ) распределения размеров кусков породы по объему (или по массе), теоретически обоснованной в работе [7], к функции распределения размеров кусков по числу частиц F_{n ( d )}, где d – диаметр кусков, что описывается следующим выражением:

d

,f d2dF (d)

F n ( ^d ) = dh -------,            (3)

• 1    dF(d)d2

d ₀

где d ₀ и d ₁ – наименьший и наибольший размеры кусков.

Для вычисления числа кусков i -й фракции предлагается формула:

Ni(d)=W, di                        (4)

где W_i – содержание i -й фракции (по объему) в массиве, %; d _i – средний диаметр кусков i -й фракции, м.

Анализ грансостава насыпных отвальных массивов показал, что суммарное содержание фракций (по объему) с размерами кусков меньше d аппроксимируется выражением:

W i ( d ) = 81,5 · d ^0,2754 .                  (5)

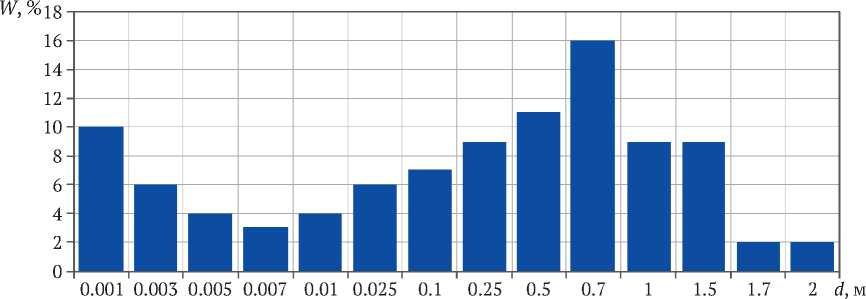
Рис. 2. Гистограмма дифференциального содержания кусков соответствующих фракций в отвале

Fig. 2. Histogram of the differential content of lumps of the corresponding fractions in the waste dump

2021;6(4):259–266

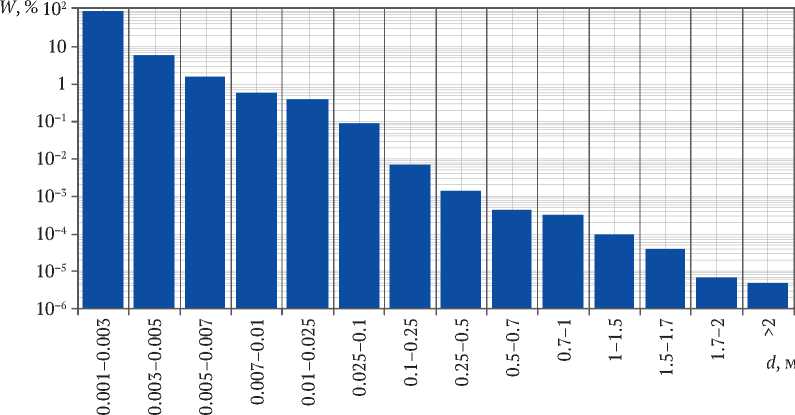
Рис. 3. Интегральное содержание W_{D ( d )} фракций соответствующего диаметра d (по числу частиц) Fig. 3. Integral contents W_{D ( d )} of fractions of the corresponding diameter d (by number of particles)

Величина коэффициента корреляции регрессионной модели (5) R ² = 0,991, что позволяет судить о достаточно высокой ее адекватности.

Интегральное процентное содержание W_D ( _d ) фракций пород отвалов по числу частиц (усредненные значения для Северного, Среднего и Южного Кузбасса) представлено на рис. 3.

Значения интегрального содержания фракций W_D ( _d ) по числу кусков аппроксимируются обратной степенной зависимостью:

W D ( d ) = 9 · 10 ^-5 d ^–1,9699 . (6)

Коэффициент корреляции регрессионной модели (6) R ² = 0, 9855.

Значения, полученные по формуле (6), интегрального содержания кусков по числу частиц используются в качестве исходных данных для определения размера кусков породы при численном моделировании насыпных массивов из разрушенных скальных и полускальных пород при использовании алгоритмов моделирования, не позволяющих учитывать данные гранулометрического состава по объему или по массе [18, 20].

Выводы

• 1.    Неоднородное строение отвальных массивов в большинстве случаев обусловлено особенностью гравитационного массопереноса складируемых в отвал пород, связанной с различной крупностью кусков коренных пород вскрыши.

• 2.    Соотношение длины, ширины и толщины у кусков взорванных горных пород составляет 1:0,85:0,8, что соответствует удлиненно-уплощенной форме частиц. Это требует значительного числа координат при описании положения кусков в массиве, а также учета моментов инерции при моделировании движения таких частиц до достижения ими устойчивого положения. Для учета неизометричной формы частиц при моделировании может быть использовано современное некоммерческое и коммерческое программное обеспечение при наличии необходимых аппаратных мощностей.

• 3.    Выбор размера кусков d при математическом моделировании структуры насыпного массива производится либо по интегральному содержанию фракций в массиве по объему (или по массе) по зависимости W_i ( _d ) = 81,5 · d ^0,2754, либо по интегральному содержанию фракций в массиве по числу частиц по зависимости W D ( d ) = 9 · 10^–5 d ^–1,9699.

Полевые наблюдения показали, что нижняя часть отсыпанных по бульдозерной периферийной или экскаваторной технологии отвальных массивов сформирована крупной фракцией со средним размером кусков d _ср = 0,8–1 м, средняя часть – кусками породы размером d _ср = 0,4–0,6 м, верхняя – преимущественно мелкой фракцией с размером кусков менее 0,1 м. Неоднородность физико-технических параметров фракционированных по высоте отвалов определяется неоднородностью их текстурных характеристик.

2021;6(4):259–266

2021;6(4):259–266