Гравитационные поля электромагнитной природы

В общей теории относительности (ОТО) гравитационные поля представляют собой искривление метрики пространства-времени. В отсутствии гравитационных полей, в инерциальной системе отсчета метрика пространства-времени галилеева, т. е. соответствует геометрии четырехмерного псевдоевклидова пространства с метрическим тензором

1 О О О ) Сgi(k0) 0 0 1 О О 1 О О (1) vO О О 1 . Рассмотрим четырехмерное пространство с декартовыми пространственными коорди- натами x    x, y, z и временной координатой x ct . Искривление метрики пространства- времени происходит при наличии макроскопических тел или электромагнитного поля [1]. При этом геометрия пространства-времени становится неевклидовой, что может быть интерпретировано как появление гравитационных сил в инерциальных системах отсчета. Локально инерциальная система отсчета с гравитационным полем эквивалентна некоторой неинерциальной системе отсчета. Квадрат интервала в искривленном пространстве-времени имеет вид ds2     gikdxidxj.                                              (2)

Здесь производится суммирование по повторяющимся индексам, т. е. под данной записью мы будем подразумевать произведение ковариантного тензора g на контравариантный

тензор dxⁱdx^j . Переход между ковариантной и контравариантной формами тензоров осуществляется через метрический тензор, например:

В” ₌ дИд_тк_Вк .                                     (₃)

Компоненты метрического тензора подчиняются уравнению гравитационного поля

8 G      1

ik        4 ik g Sik ,

c 2

где G = 6, 77-10 11 м3 кг С2 - гравитационная постоянная; с = 2, 99-108 м/с - скорость света в вакууме; Tk - тензор энергии-импульса; T = Т - след тензора энергии-импульса; Rik - тензор второго ранга, который можно получить из тензора кривизны четвертого ранга R"mk, сумми- руя по индексам n и m:

mm

RRm ik        imk

ik        im     m ^l      ml

6xm     dxk      lm ik lk m, где m – символы Кристоффеля, определяемые выражением

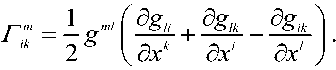
Тензор кривизны четвертого ранга определяется следующим выражением nn

Rn           ik          im        n l        n l imk          mklm ik       lk im

Тензор энергии-импульса электромагнитного поля

Рассмотрим уравнения гравитации при отсутствии макроскопических тел, при этом в пространстве может находиться электромагнитное поле. В этом случае тензор энергии - импульса определяется только электромагнитным полем и имеет вид

¹ l     ¹ lm

,

ik                il k          lm      gik где Fik - тензор электромагнитного поля. Здесь для упрощения выражений используется га уссова система единиц              . Тензор электромагнитного поля определяется через

4- потенциал A :

AA

F . = A . - A. k = —Lт

ik      k;i      i'k     Xx'Xx где A составляется из векторного и скалярного потенциалов электромагнитного поля (A2e3=Ax,A ,Az и A = -фу. Ai;t- ковариантная производная от 4-потенциала:

ХД

A =—r-rm A .(10)

i; kik m

Тензор электромагнитного поля можно записать через напряженности электрического и магнитного полей:

0	H z	H y	E x
H F z	0	H x	E y
ik      H y	H x	0	E z  ’                            (11)
E x	E y	E z	E x

1A где E =----grad(/>, H = rotA . Для того чтобы выражение для тензора энергии-импульса ct электромагнитного поля не зависело от метрического тензора, запишем тензор энергии-импульса электромагнитного поля в смешанной форме:

Т ^к = — | F,F “ -¹ F F lm8^k |, i      ₄ il         ₄ lm       i

где 8( = g_ug^,i - единичный тензор; 8* = 0 при 1* к и 8* = 1 при i = k . Тензор энергии-импульса обладает тем замечательным свойством, что его след равен нулю, т. е. Т = Т = 0. В смешанной форме тензор энергии-импульса электромагнитного поля имеет вид

¹ ( E ² E ² E ² ₂ xyz

H ² H ² H ² ) xyz

EE HH xy    x  y

EE xz

HH xz

EH y

EH zy

k

i

EE HH

x

y   xy

¹ ( E ² E ² E ²

₂ x      y      z

H ² H ² H ² ) xyz

EE yz

HH yz

EH zx

EH x

EE HH xz    x z

EE yz

HH yz

¹ ( E ²   E ²

₂ x     y

E ² z

EH EH yz  zy

EH zx

EH xz

_H 2   _H 2   _H 2 ₎

xyz

EH EH xy  yx

EH EH yz  zy

Временная компонента тензора энергии-импульса связана с плотностью энергии электромагнитного поля То0 = —го, компоненты T а,Р = 1, 2, 3 образуют тензор плотности потока импульса электромагнитного поля, и компоненты Т0 6Z = 1, 2, 3 связаны с вектором плотности импульса электромагнитного поля T 0 cP . Полученное выражение тензора энергии-импульса электромагнитного поля в криволинейных координатах не зависит от метриче- ского тензора.

Уравнения гравитации при наличии электромагнитного поля

При отсутствии макроскопических тел уравнения гравитационного поля запишутся в виде (Т = 0):

8 G

Ri k        4 T ik *

c

Вследствие квантовых эффектов классическая электродинамика становится противоречивой при сильных полях. Наличие сильного электромагнитного поля сопровождается рождением частиц из вакуума, поэтому электромагнитное поле в «чистом» виде, без частиц, возможно только при слабых полях. Мы будем рассматривать классические, слабые электромагнитные поля, т. е. в нашем случае напряженности электрического и магнитного полей m ² c ³

ограничены снизу величиной----, где h - постоянная Планка; m, e - масса и заряд электро- he на. Такие поля, вследствие малости G, будут приводить к малым искривлениям пространства-времени, поэтому можно пользоваться первым приближением (ньютоновским приближением) для уравнений гравитационного поля. В этом случае метрика пространства-времени близка к галилеевой метрике и компоненты метрического тензора могут быть записаны в следующем виде gik    gik    hik где h – малая поправка к галилеевой метрике.

Так как гравитационное поле создано слабым электромагнитным полем, то поправка к тензору энергии-импульса вследствие искривления пространства-времени является величиной большего порядка малости, т. е. ковариантный тензор энергии-импульса T можно рас- считывать в галилеевой метрике:

Tik   gimTk    gim Tk + h Tm   gim TkT

ik        im k         im k        im k         im kik причем T 0T ,T 0T0a,P =1,2,3 . ,   00             0        ,           ,,

Выражение для R в первом приближении имеет вид

R ik       2

A

c ² t ²

h, ik

3   5 2

где ^A=Z^ – оператор Лапласа, а □ = 15 x ²

^{1 5 2} c ² t ²

– оператор д’Аламбера. Уравнения

гравитационного поля при наличии только электромагнитного поля принимают простой вид

1 9 2

c ² "дt ²

h ik

16 G 0

4    ^Tik  ^.

c ⁴

Например, для электростатического поля R

1                E ²

_ГР и T ₀₀      , где ф – потенциал

статического гравитационного поля, уравнение для временной компоненты тензоров имеет вид

2 GE ²

ГР      _c 4

.

Полученное выражение – это уравнение Пуассона, определяющее распределение гравитационного потенциала. Решение уравнения зависит от напряженности электростатического поля, т. е. распределение гравитационного потенциала в пространстве определяется электростатическим полем.

Безусловно, гравитационное поле, созданное электромагнитным полем, слабо и не может быть обнаружено в современных экспериментах, но удивителен сам факт существования связи между, казалось бы, совершенно различными объектами природы – электромагнитным и гравитационным полями.