Greedy heuristic method for location problems

F ( X 1 , ...,X k ) =

= argmin X 1 , X_{k 6} R d Z "i min X _e { X 1, ..., X k } 11 4 - X I12 .

F ( X i , ..., X_k ) =

• = argmin X i , ..., X k e R d Z N - 1 w min X e { X i , .... X k } ^{L (} 4- ^X Y ⁽

Here, w i > 0 are weight coefficients. In the case of k -means problem, all w i = 1.

^{F (} X 1 , -, X k ) = argmin X 1 , ..., X k { A i , ..., An }^X

• ^X Z N - 1 w i min X { X 1 , ..., X k } L ⁽ A , X ) .

Known methods. The most commonly used algorithms for solving k -means problem include the ALA procedure (Alternating Location-Allocation) which repeats two simple steps:

Algorithm 1. ALA procedure.

Required: data vectors A 1 … A N , k initial cluster centers X 1 … X k .

• 1.    For each center X i , define its cluster C i as the subset of data vectors having closest center X i .

• 2.    For each cluster C i , recalculate its center X i :

• 3.    Repeat from Step 1 is steps 1, 2 made any changes.

X i = argmin Z wL ( X , Y ) .

X   Y e C i

The “classical” k -means method with squared Euclidean distances ( l 2² ) has an important advantage. In this case, new cluster center recalculation is a simplest task solved in a single step. An average (weighted average) value of each coordinate in the cluster is the corresponding coordinate value of the center [1]. If i th cluster center X_i = ( x_{i ,1}, …, x_i,d ) is a d -dimensional vector and data vectors A j = ( a i ,i , ..., a j, _d ), J = 1, N are also d -dimensional vectors then new center of i th cluster for the k -median problem is [1]:

^x i , k = Z y e c i w i y k / Z w,^k = ¹> ^d .

If the ALA procedure runs with the rectilinear metric ( l 1 ) then the value of each cluster center coordinate is calculated separately as median (weighted median) value of the corresponding coordinate of data vectors which are cluster members. Such procedure can be described as follows.

Algorithm 2. Calculating i th cluster center (median) with the l 1 metric.

• 1.    For each k = 1, d :

  • 1.1.    Arrange data vectors A i = ( a j . ₁, ..., a j _d ) e C i in ascending order. Denote such sequence a '_{1, k} , ..., a ' _{Ci , k} . Here C_i is the power of a set.

    1.2. Calculate m =

    
    
    

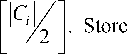
    = a ' m , k . Here,

    
    

square brackets mean integer part.

• 1.3.    Repeat 1.

• 2.    Return X i = ( x ' 1 ..., x i , d ) .

The result of the ALA procedure depends on selection of the initial centers. Usually, initial centers are selected among data vectors. The k -means++ procedure [12] is preferred in comparison with the chaotic selection of the initial centers. The k -means++ procedure guarantees accuracy O (log( p )). However, such accuracy cannot be acceptable for most practically important problems. In this case, various initial centers recombination techniques are used.

Authors propose many techniques optimizing the ALA procedure: sampling [13] (solving a simplified problem on a randomly selected subset of data vectors and using the result as the initial solution for solving the initial problem), various streaming algorithms for running on big data [14] etc.

Dependence of the ALA and other local search procedures on the given initial data embarrasses the reproducibility of the results: the same data vectors can belong to different clusters or the same cluster depending on chosen initial centers. Thus, problem of developing an algorithm resulting in precise and stable result is needed.

Perfect results of clustering and classification problems can be obtained by using the Information Bottleneck Clustering method (IBC) [15]. Running this algorithm starts with considering each data vector as a separate cluster. Then superfluous clusters are eliminated one by one unless we have k clusters. Each time, this algorithm eliminates the cluster center which gives minimal total distance increase after its elimination. Such algorithms are extremely slow [15]. Genetic algorithms with greedy heuristic [16] use the same principles. However, such algorithms developed initially for solving the k-median problems on a network are compromise methods which allow solving bigger problems. Versions of such algorithms described in article [17] can be used for solving continuous problems. The approach can be described as follows [2].

Algorithm 3. Genetic algorithm with greedy heuristic for k -median problems.

Required: Population size N p .

• 1.    Form (randomly with uniform distribution or using the k -means++ procedure) Np different initial solutions X 1 , ..., X Np ^ {1, N }, | xi| =k V i = 1 ,N p . Each of such solutions is a subset of power k used as an initial solution of the ALA procedure. Here and after, for each of the initial solutions, the fitness function Ff itness ( x ) is evaluated by Algorithm 4. Resulting values are stored in variables f 1 , ..., f N _p.

• 2.    If the stop condition is reached the STOP. The result is the initial solution χ having the minimal corre- i

• 3.    Select randomly two indexes   k 1 , k 2 e {1 ,N },

• 4.    Form an interim solution x _c = x _k 1 и x _k 2 ■

• 5.    If χ c >k then go to step 7.

• 6.    Calculate j * = argmin F^ ( x c { j '} ) ■ Eliminate j * J ^e X c

• 7.    If 3 i e {1 ,N_p } : x i = X _c then go to step 2.

• 8.    Select index k 3 e {1 ,N_p } as follows. Select randomly two indexes k 4 , k 5 e {1 ,N }. If f_k 4 > f_k 5 then k ₃ =k ₄else k ₃ =k ₅.

• 9.    Replace χ k 3 and corresponding fitness function Value: X k ₃ = X c , fk ₃ = ^F fitness ( X c ) . ^{Go to ste}P ^2.

sponding value f_i . For finding the final solution, Algorithm 1 runs again.

k 1 ^ k ₂.

from χ _c : χ _c= χ _c\ { j^* } . Go to step 5.

Steps 5, 6 of this algorithm realize so called greedy heuristic eliminating sequentially the centers from the interim solution.

Analogous greedy heuristic was proposed in 1963 by Kuehn and Hamburger [18]. The Information Bottleneck Clustering method is based on the same principle of sequential cluster elimination [15]. Both method of Kuehn and Hamburger and the IBC method form the initial unfeasible solution as the set of all data vectors.

The fitness function can be evaluated as follows:

Algorithm 4. Calculating fitness function Ff_itness ( x ) .

Required: initial solution χ .

• 1.    Run Algorithm 1 from initial centers { A i Ii e x}, form set { X ₁ , ..., X_p } of centers.

• 2.    Return F itness ( X ) = X ^N = 1 W min, L ( X j ^,A i ) . j e {1 ,p } '

An indisputable advantage of the Information Bottleneck Clustering method is its determinancy: this method does not use any random values, thus, each run results in the same result. In general case, if an algorithm uses random values, the precise reproduction of the results is impossible. Using the IBC method slows down the computation utterly. Thus, development of an algorithm giving sufficiently precise results is important for solving many practical problems.

In [3], authors propose a modification of the greedy heuristic used at step 6 of Algorithm 3. In this case, sets of points representing cluster centers in d -dimensional space are used as an alphabet of the genetic algorithm instead of the sets of data vector indexes. Authors call such modification Genetic Algorithm with Floating Point Alphabet. Results of the genetic algorithm, with this new heuristic are significantly more precise than the results of the modification proposed in [17] ( k -problem solution, in fact). At the same time, iterations of Algorithm 3 with this heuristic can be performed faster in comparison with using Algorithm 4. Moreover, abrupt decrease of the computational complexity of step 6 of Algorithm 3 allows using this algorithm for large-scale problems: in [3], authors present results for problems up to 560000 data vectors. Such heuristic can be described as follows [3].

Algorithm 5. Greedy heuristic for the genetic algorithm with floating point alphabet used instead of steps 4–7 of Algorithm 3).

Required: set of data vectors V = ( A 1 , ..., A N ) e R d , quantity k of clusters, two “parent” sets of centers χ k 1 and χ k 2 , parameter α.

• 1.    Set x _c= X _k 1 и x _k 2 . Run ALA procedure from initial set of centers χ c . Store the result to χ c .

• 2.    If χ c =k then start the ALA procesure from the initial solution χ c then STOP and return the result χ c .

• 3.    Calculate distance from each data vector to the nearest center in χ c :

d i = min L ( X , A i ) V i = 1, N .

X e x c

Form clusters around centers χ c :

C i = arg min L ( X, A i ) V i = 1, N .

X e x _c

Calculate distances from each data vector to the second closest center in set χ c :

• d: = min L ( Y , A ) V i = 1, N .

• 4.    For ezch center X e x_c , calculate 8 X = F ( % c \ { X } ) = I_C X e C i ( D - d i )

• 5.    Calculate n _s = max { [ a ( |x c |- k ) ] ,1 } . Sort values δ X in ascending order and select subset x e ii _m = { X i , ..., X n } of n s data vectors with minimal values δ X .

• 6.    For each j e { 2, |x e _Hm| } : if 3 q e { 1, ( j - 1 ) } : L ( X j , X_q ) < L min then remove X j from set x _{e Hm} . Here, ^L min = min { ^max { ^L ( ^X , ^X j ) , ^L ( ^X , ^X q ) } } ’

• 7.    Store x c = x c \ x e lim .

• 8.    Rearrange the data vectors to the closest centers:

• 9.    For each X e x _c : if 3 i e { 1, N } : C i = X and C i* ^ X then recalculate center X * of cluster C Xus = { A | C = X , i = 1, N } . Store x c = ( x c \ { X * } j u { X } .

• 10.    Go to step 2.

Y e x c \ { C i }

C i* = arg min L ( X , A i ) V i = 1, N .

x e x c

Here, an importan parameter α determines the part of superfluous centers eliminated in a single iteration. Autrors [3] propose value 0.2. Higher values accelerate the algorithm but reduce the preciseness. Small values lead to eliminating the centers one-by-one in accordance with Algorithm 4. In this paper, we used value 0.25.

Iterations of this heuristic combine the fast greedy heuristic [16; 17; 19] eliminating up to 20–25 % superfluous centers with an iteration of the modified ALA procedure. Algorithm 4 requires p ( k 0 - k ) runs of the ALA procedure (here, k ₀ is quantity of initial centers), Algorithm 5 reduces number of iterations down to O (log( k 0 – k )). Moreover, each iteration does not require running the whole ALA procedure. Instead, only its separate optimized steps (location – allocation) are performed.

Obviously, if k 0 = N then Algorithm 5 is similar with the Information Bottleneck Clustering: number of centers (and clusters) at the first iteration coincides with the number of data vectors. Moreoved, if k 0 = N is not random. Thus, a simple deterministic algorithm can be constructed [20].

Algorithm 6. Deterministic algorithm with greedy heuristic.

Required: set of data vectors V = ( A 1 , ..., A N ) e R ^d , number of clusters k , parameter α.

• 1.    Set χ c =V .

• 2.    Start Algorithm 5 from step 2.

Table shows somparison of results of various algorithms. This algorithm is deterministic but not very precise.

New algorithms. Deterministic Algorithm 6 is a special case of Algorithm 6 with initial value χ c =N . The crossover procedure of the genetic algorithm with floating point (Algorithm 5) starts from a joint interim solution x _c = x_k 1 ^u x k 2 . If k <<  N then in most cases (at least at the initial iterations of the GA), elements of the “parent” sets χ k 1 and χ k 2 do not coincide and Algorithm 5 has χ c = 2 k at its initial iteration. In [21; 22], authors propose various efficient modifications of the greedy heuristic for genetic algorithm with partial joining of the “parent” sets. In this case, |x _c | e { ( k + 1 ) ,2 k } . The GA with recombination of fixed length subsets [10] operates sets of power k only. All listed algorithms are most efficient for different problem classes. Thus, depending on problem class, various power χ c of the initial solution can be optimal.

Let us denote quantity of centers in the initial solution as k init = χ c and a ratio of the superfluous centers to k init as

P = ( k_mU - k ) / k .

Greedy heuristic in its original form (steps 4–7 of Algorithm 3) and modified form with floating point alphabet (Algorithm 5) can be used as a standalone method for solving the problem. An algorithm can be described as follows.

Algorithm 7. Greedy heuristic method with multistart.

Required: sed of data vectors V = ( A 1 , ..., A N ) e R d , number k of clusters, parameters α and β.

• 1.    Calculate k_init =k +[ в k ] . Select randomly subset x с e V of power k nit .

• 2.    Start Algorithm 5 from step 2.

• 3.    Check the stop conditions and repeat from step 1.

Such approach requires indicating the value of parameter β. Results given in table (see algorithm “GH”) show the importance of this parameter.

Let us consider a known method of solving pseudoBoolean optimization problems, Probability Changing Method [23–25]. The main idea of this method is selecting elements from some given set randomly in accordance with the probability vector depending on previously aclieved results. An algorithm based on this method was proposed for solving the p-median problem on a network [26; 27]. However, such algorithm has very slow convergence and can be used as an aiding method for the genetic algorithm [26]. Similar algorithm can be used for approximate solution of the k-median problem with an arbitrary distance function [28]. Inclusion of the greedy heuristic into the Probability Changing Method leads to new efficient algorithm:

Algorithm 8. Adaptive greedy heuristic method for continuous location problems.

• 1.    Set equal values of probabilities p_i = 1 / N for all

• 2.    For each j = 1, N pop do:

  • 2.1.    Copy the probabilities q i = p i for all i = 1, N . Set X c =0 . Generate randomly r e [ 0; 2 ) with uniform distribution. Calculate k_init = k + Г в rk ] .

  • 2.2.    While |x c | <  k nt do:

    • 2.2.1.    Generate random Q e Г о; X N q ) with uniform distribution. Set S = 0; l = 1.

    • 2.2.2.    While S + q j <  Q do: S = S + q j ; l = l + 1; repeat 2.2.2.

    • 2.2.3.    Set x c = X c ^u{ A } ; set q i = 0.

    • 2.2.4.    Repeat 2.2.

  • 2.3.    Copy the initial set £ _c = x _c .

  • 2.4.    Start Algorithm 5 from step 2. Store the result f_} = F ( x c ) ; set x j = x c ; ^в j = ( ^k _mU - k ) / k .

  • 2.5.    Next iteration 2.

• 3.    Calculate в = в X _N , pp .¹_N , j = 1 X N = 1 op ( N pop - n j ) X ^N = 1 ^op в J

• 4.    Chose index b having minimal corresponding value f b and index w having maximal f w .

• 5.    For each i = 1, N do:

  • 5.1.    If A i e £ b and A i £ £ _w then set p i = y p i . Else if A i e £ _w and A i £ £ b then p i = p / y .

  • 5.2.    Next iteration 5.

• 6.    Check the stop conditions and repeat step 2.

i = 1, N . Set в = 0.5.

Npop        в l ( Nnn n - n I )

here, n j is the number of value f j in an ascending sequence os these values.

If 4в k >  N then set в = N /4 k .

This algorithm requires indicating values of parameters N pop (population size) and γ (probability change coefficient). Small populations are enough for this algorithm. We used N pop = 9 and γ = 1,1. Parameter β is adjusted with special meta-heuristic (step 3).

New algorithms and the deterministic algorithm with greedy heuristic [20] have an important feature. Many clustering problems (see for example [19]) are decomposed into series of k-means problems with k = km, km„ where kmin = 1 (the whole data set is min max m n supposed to be a single cluster) and kmax is equal to some reasonable value. Algorithm 6 can be used for a problem with k = kmax and then Algorithm 5 from step 2 can be started again for obtaining other results down to k = kmin. Thus, all results for k = kmin, kmax can be obtained in a single loop.

In many cases, a single start of the greedy heuristic cannot be completed within the given time limit. Running time of the algorithm depends on parameter β. In such cases, table contains dashes. Problems with data sets are not solved with deterministic algorithms either due to huge amount of time needed.

The optimal value of parameter α remains an open question. Note that if α = 0.001 then centers are eliminated from the interim solution one-by-one in accordance with the original greedy heuristic. For the deterministic algorithm with greedy heuristic [20], value α = 0.25 guarantees faster result (not the most precise) in accordance with results obtained with α = 0.001. In the case of stochastic algorithm, it is not easy to foresee which value leads to better result in reasonable time. As we can see in table, data vectors quantity (compare data sets MissA-merica1, BIRCH3 and examination of diodes) and metric do not determine the optimal value of this parameter. Developing a meta-heuristic algorithms adjusting this parameter seems to be promising. Adjusting parameter α with fixed value of β can be easily performed. Simultaneous adjustment of both parameters requires factor analysis for evaluating the influence of each parameter on the results. Thus, developing a co-evolutionary algorithm with two concurrent populations having different fixed values of parameter α seems to be simpler. An example of analogous algorithm with concurrent populations evolving with various bionic algorithms was proposed in [30].

Nevertheless, it is obvious that new adaptive algorithm allows to obtain better results than multiple start of the ALA procedure and multiple start of the greedy heuristic with fixed β.

Used algorithms: “ALA” is ALA procedure multistart; “GA-MIX” is genetic algorithm with fixed length subsets recombination [10]; “GA-GHFP” is genetic algorithm with greedy heuristic and floating point alphabet [3]; “GA-classic” is GA with classical recombination, “IBC” is Information Bottleneck Clustering [15; 20]; “Determ. GH” is deterministic algorithm with greedy heuristic [20]; “GH” is new Algorithm 7; “GL” is multistart of the original greedy heuristic with local search (steps 4–7 of Algorithm 3 at α = 0.001 or steps 4–7 of Algorithm 3 with fast elimination of centers from the interim solution similar with steps 5–7 of algorithm 5 at α = 0.25); “GH” adapt is adaptive greedy heuristic (Algorithm 8). If no result was achieved within specified time limit, the table contains a dash.

Results of various methods

Completion of table

Data set, number of data vectors, dimension, data type	Number of clusters k , metric, problem type	Algorithm	Time, sec.	Average result of 30 runs: total distance (2) F ( X 1, …, Xk )		Std. deviation of the result (30 runs)
				Parameter α = 0.25	Parameter α = 0.001	Parameter α = 0.25	Parameter α = 0.001
Generated problem,	20, metric	ALA	4		4461.24		25.9199
N = 500, d = 2, real	based on	GA-MIX	4		4509.49		14.4368
	angular,	GA-GHFP	4		4326.72		4.7587
	distances, k -	GA-classic	4		4392.95		79.6913
	median	IBC	3141		4381.34		Determ.
		Determ. GH	4.9/23.5	4377.12	4376.43	Determ.	Determ.
		GH, β = 0.5	4	4350.36	4378.30	15.1717	15.4234
		GH, β = 1	4	4333.02	4371.50	5.8614	38.5620
		GH, β = 3	4	4389.32	–	22.5053	–
		GL β = 0.5	4	4428.97	4453.65	59.4167	34.3130
		GL, β = 1	4	4379.42	4359.41	46.1732	22.5052
		GL, β = 3	4	4429.37	–	78.2398	–
		GH adapt.	4	4313.67	4309.43	3.7077	1.4427