Группа Ли-Беклунда и законы сохранения уравнений анизотропной идеально пластической среды

О _х - 2k( 6 ) ( 6 _xcos 2 6 + 6 _у sin 2 6 ) - 6,

O _y-2k( 6 )( 6 _xsin2 6 - 6 _ycos2 6 )-0,        (1)

где о - гидростатическое давление; 6 - угол между осью Ох и первым главным направлением тензора напряжений; вид функции k( 6 ) устанавливается по опытам на принудительный сдвиг образцов пластической среды по различным направлениям; индекс внизу означает дифференцирование по соответствующей переменной.

На функцию k( 6 ) по физическим соображениям накладываются следующие условия: k( 6 ) - k( 6 + п / 2); k( 6 ) ^ О; k( 6 ) - ограниченная функция.

Отметим, что случай k - const отражен в [3] и здесь рассматриваться не будет.

В системе (1) введем новые переменные по следующим формулам:

у + J к ( и ) d и = з, у- J к ( и ) d и = ^ , о - ( ^ + п ) / 2, J k( 6 )d 6 - F( 6 ) - ( П - S ) / 2.

После этой замены уравнения (1) приводятся к виду д£ + D^tg 6 -6, д _х П - d _y n ctg 6 -6.

Поменяем ролями зависимые и независимые переменные, т. е. считаем, чтох -х( ^ , п ),у -у( ^ , П ). Тогда при условии, что якобиан перехода

7-0(х,у)Л0( ^ , п )

отличен от нуля, получаем дПУ + дпxtg 6 - 6, д^у-д^х^ 6 - 6.       (2)

В системе уравнений (2) введем новые искомые функции x , у :

x -xcos 6 +ysin 6 , у --xsin 6 +ycos 6 .

В результате получим систему уравнений д^Х +у/(2к)-0,дп y+x/(2k)-0,(3)

где

k(6)-k(F-1((n-^)/2)).(4)

В системе (3) введем обозначения

Л. VЛ. V x = ^ + з, у = ^-з, тогда эта система перепишется так:

д у Х -д у Х + f ( у ) у = 0, д Х у -д у у + f ( у ) Х = 0.

Запишем систему (3) следующим образом:

^д Х ^{и -д} _y ^{u + f} ( у ) v = °, ^д x ^{v -д} _y ^{v + f} ( у ) ^u = ⁰              (5)

Симметрии уравнения (5). Оператор универсальной линеаризации для системы уравнений (5) имеет вид

Для

' Dx + D_y    f '

, f    D x + ^D ^ ,

поиска симметрии следует решить уравнение

l_Fg = 0, I f =

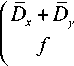
Dx + Dy xy где D Х = дx + ulдu + ulдv + ... + uk +1дuk + vk +1 дvk + ... ;

^D у =д у + (- ^u i - jv )д u + ( ^u i - ^fu )д v +.... +

+( - uk +1-vkf )д uk + (vk +1-ukf )д vk + ...,             здесь uk = дku I дxk, vk = дkv I дxk . Функция uk = дku I дxk зависит только от переменных х,у, и, v, и, v. Если функция g зависит только от переменных х,у, и, v, uk, vk, то будем писать ge 3k.

Классические симметрии уравнения (5). В этом случае производящая функция симметрии g - (ф, у) зависит от переменных х,у,u, v, ux, vx, u^, vx, a g - от переменных х,у, u, v, ux = ul, vx = vl, поэтому она принадлежит классу з,.

Запишем уравнение I F g = 0 в этом случае в развернутом виде:

Ф х ^{+ U} № , ⁺ “ 1 Ф р ^{+ U} 2 ^Ф и 1 ^{+ V} 2 ^Ф V ⁺ Ф у ^{+ (- U} 1 -^ Ф и + (v , -N Ф v + + (-U 2 -^ Ф и, + ^ -fu) Ф„ + ^ = 0,    (7)

Ф х ^{+ U} 1 V u ^{+ U} 1 V v ^{+ U} 2 ^ф и , ^{+ v} 2 ^ф V , ^- Ф у + ^{( U} 1 Жф и ^{-- ( v} 1 ^-/^UM ^{+( U} 2 ./V- ^{) Ф} и , ^{- ( v} 2 ^-.К) ^ф V , ' . ^{/ Ф} °.

Поскольку Ф и ф не зависят от и₂, v₂, а выражения (7) есть полиномы первой степени по этим переменным, то коэффициенты при и₂, v₂ необходимо равны нулю. Следовательно, ф v , =0, ^ф и , = 0. Отсюда

Ф =А¹и+В¹, ф = АФ + В²,А¹,В¹ е 3 ₀.

Подставляя эти соотношения в (7), получаем полиномы относительно переменных и1, v1. Приравняем к нулю коэффициенты при этих переменных:

Ф = А^хи + B⁰v + А" и + Л¹, ф = би + b°v + a⁰u + Л^х, где А¹, В¹, а¹, Ъ¹, Л - функции только переменных х,у, которые определяются по десяти уравнениям:

bX — b‘y = 0, AX + АУ = 0,(8)

2a0 +/(А1 - Ъ1) = 0, 2 В0 +/(Ъ1 - А1) = 0,(9)

/(А0-Ъ0) + aX - a = 0,/(Ъ°-А°) + B^ + By =0, (10) Ж-В0)+ b - by0 =0,/(a0 + B0)+ A + Ay0 =0, (11) hX + hy + fh2 = 0 ,hlx + hy + fh2 = 0.(12)

По уравнению (8) получаем

Ъ¹ = G¹(x+у),A¹=F¹(x-у), где G, F- произвольные гладкие функции.

Из уравнения (9) вытекает a0 = 2 /(G1 -F1), В0 = 2 /(F1 - G1).      (13)

Поскольку a0 + В0 = 0, то из (11) имеем

У ° = С³(х+у),А⁰=С⁾(х-у).

По уравнению (10) получаем B y = 0 , следовательно В⁰= ю (х), а отсюда, с учетом (12),

^to^^-G1)-1.

По второму равенству (10)

/=to' (х)(С G ) '.

По этим двум соотношениям ясно, что оба они удовлетворяются, если ш = ехр(ах),/= ехр(-ау). По физическим соображениям ясно, что / такой быть не может и поэтому/- произвольная функция, а следовательно,

G1= F1= const, G0 = F0 = const.

Поэтому симметрии в классическом случае имеют вид о = А1и1 +А0и + Л1(х,у), ф=АН1+АФ + Л2(х,у),            (14)

где (Л1, Л2) - произвольное решение исходной системы уравнений (12).

Базис классической алгебры Ли, допускаемой системой (5), выглядит так:

\

u е -   1

*Ф =1

I ^V ,

Г и 1

, ⁵ 0 I

I V

\

, Н =

Г h h2

,

а таблица умножения имеет вид

{ 5 , , 5 0 } = 0 , { 5 0 , H } = - H , { 5 , , н } =

'д h ^, /д x' д h ² /д x

Высшие симметрии уравнения (5). Вычислим симметрии второго порядка, т. е. те симметрии, когда производящая функция зависит от х,у, и, v, и^ v₁, и₂, v₂.

Нетрудно показать, что производящие функции симметрий имеют вид

Ф =A2u2+A1u1 + B1v1+A0u + B0v + Л1, ф = Ъ2и2 + a1 и1 + Ъ1и1 + a0 и + ЪФ + Л2, гдеА1, В1, а1, Ъ1, Л1 - функции только отх,у, удовлетворяющие следующим уравнениям:

AX + Ay = 0, bX — by = 0,(15)

2B1+/(Ъ2-A2)=0,2a1+XA2-Ъ2) = 0,(16)

AX + Ay + f(B, + a,) = 0, bX-by + f(B, + a,) = 0, (17) BX + By + 2B0 + f (bl - A1) = 0, a X - ay + 2 a0 + f (Al - b,) = 0,(18)

Ax⁰ + A y + f ( B ⁰ + a °) = 0 , a X - a + f ( A ⁰ - b °) = 0 , (19) B X + B y + f ( b ⁰ - A °) = 0 , b X - b y + f ( B ⁰ + a °) = 0 . (20) По уравнению (15) получаем

А2 = F2 (x -у), Ъ2 = G2 (х +у).

По уравнению (16) следует

В1 = 1/2(F2-G2),a1 = 1/2(G2-F2).

Поскольку

В1+а1 = 0, то из (17) имеем

А1=F1(х-у),Ъ1 = G1(х+y).

По уравнениям (19) и (20) получаем a⁰+B⁰= a y ,а⁰-В⁰=7(Ъ¹-А¹)- a X .     (21)

С другой стороны, по этим же уравнениям имеем a 0¹ - a 0 + B_x ¹ + B y¹ = 0.

xy x y

Отсюда, учитывая уравнение (21), следует a X+B1-a0 = g(x),                (22)

где £(х) - произвольная функция, появившаяся после интегрирования.

По уравнению (22) получаем

2 a X -ДЪ¹-A¹)=g(x).

Последнее соотношение дает условие на функцию/: g(x)/»=А¹-Ъ¹+ Gx² + F X .

Правая часть этого уравнения удовлетворяет волновому уравнению

Utt - U yy = 0, поэтому данному уравнению должна удовлетворять и его левая часть. Отсюда получаем, что (/(у))^-1 может быть либо линейной функцией, либо суммой экспонент, либо (c₁siny+ с₂cosy).

Любая из этих функций не удовлетворяет условиям на функцию к, если ее восстановить по условию (4). В силу этого функция/(у) остается произвольной, и по соотношениям (15)_(22) без труда получаемА¹ =В¹ = const, В¹ = а¹ = 0, (Л¹, Л²) - произвольное решение системы (5).

Окончательно производящие функции симметрии второго порядка имеют вид ф = A2 и2 + A и1 + A0 и + h', ф = A2 v 2 + A1 v1 + A 0 v + h2.

Теперь найдем общий вид симметрии b-го порядка, т. е. рассмотрим случай, когда производящая функция симметрии зависит от переменныхх,у, ир vp и2, v2, uk, vk при к> 2. В этом случае производящие функции симметрии следует искать в виде ф= A^uk + A' Тк—1 + B У—1 +... + A1 и + B^v+h, ф= bkuk + ak 1 uk _1 + bk 1 vk _1 +... + a 0 и + b 0 v+h 2, где (A1, A2) - решение системы (5);А1, 51, a1, b1 - функции только отх,у, удовлетворяющие следующим уравнениям:

A + Ay= 0 , bX _ by = 0,(23)

25 ^{i -1} ■/О .! ' ) 0,

2a‘ Ч(,Г b‘i 0,(24)

AX-1 + A; 1 + f (Bk-1 + ak-1) = 0, bX 1 _ by,-1 + f (Bk-1 + ak _1) = 0,(25)

BX-1 + By,-1 + 2 Bk _ 2 + f (bk -1 _ Ak-1) = 0, aX_‘ _ ay' + 2ak-2 + f (Ak-‘ -bk-‘) = 0,(26)

ax _ 2 + A -2 + f (Bk_ 2 + ak_ 2) = 0, bX_2 _ bk_2 + f (Bk_2 + ak_2) = 0,(27)

bX- 2 + By,- 2 + 2 Bk -3 + f (bk- 2 - Ak_ 2) = 0, aX_2 _ ak_2 + 2ak-3 + f (Ak-2 "bk-2) = 0,(28)

AX + Ay + f (B1 + a 1) = 0, b\ _ by + f (B1 + a 1)=0,(29)

B\ + By + 2 B0 + f (b1 _ A1) = 0, aX _ ay + 2a0 + f (A1 - b1)=0,(30)

A0 + Ay+ f (B0 + a 0)=0, a0 -a0 + f (A0 _b0) = 0,(31)

BX + By + f (b0 _ A0) = 0, bX _ by + f (B0 + a 0) = 0.(32)

Не накладывая на функцию/никаких ограничений, т. е. считая ее произвольной, по приведенным уравнениям без труда получаем, что

А ' = S ' = const, S ' = a = 0.

Следовательно, симметрии А-го порядка имеют следующий вид:

ф = Ak ик +... + A1 и1 +... + A0 и + hx, ф = A vk +... + A v +... + A и + h2, где А' - постоянные; (A1, A2) - произвольное решение системы (5).

Нетрудно видеть, что алгебра высших симметрий име ет вид

О | ^и п I И _( ^h

S " = V v . J H " = V h 2 J

Для описания этих симметрий удобно воспользовать ся оператором рекурсии п, который возьмем в виде

I Dx 0 V = ^X

¹ 0 D

.

Этот оператор обладает свойством l _F о V = V о l _F.

Поэтому имеем

_ s = v " (S)

Теорема 1. Алгебра высших симметрий порождается элементами S _n ,H. При этом имеют место коммутационные соотношения

{^ n ^,^_m}=^0, {^ n ^{, H} l= V ⁿ ( ^H ).

Симметрии исходного уравнения (1). Выше были найдены симметрии уравнения (5). Они были записаны в переменных X, y, 5 с , у . Здесь мы запишем их в исходной системе координат 8 , ^ ,х,у. Для этого найдем матрицу 1 , которая связывает две формы Картана:

\

। U' ^ I dX _ X^dX _ X_Ady

U '=   1 =               .

,

U =

U 2^'

U 1

| dy - у.dXc - yy,dy

2 | d a-a _XdX -a _ydy ^ = d 0-0_x dX -0 dy

7 V ^{X y} 7

I ^U 2. следующим образом:

U = 1 U' .

Эту матрицу нетрудно найти в исходной системе координат. Она имеет вид

(a, sin 0 - a,, cos 0 -a, cos 0 - a,, sin 02 xy   xy

0_x sin0-0_V cos0 -0_x cos0-0_V sin0 ‘

X yX y

Теперь пересчитаем точечные симметрии. Нетрудно видеть, что производящей функции S1 соответствует сим

11 2ж метрия , которой в свою очередь отвечает инфини-

10 J тезимальный операторА= дa. СимметрииНотвечает производящая функция

Я =

(a v sin 0 - с? v cos 0)Л2 -(о х cos 6 + о v sin 0)/^ (0 v sin 0 - 0 v cos 0)Л2 -(0 v cos 0 + 0 v sin 0)^

Ее можно переписать в инфинитезимальном виде:

A_H = (A^os 0 - A₂sin 0 ) д _х + (A₁sin 0 - A₂cos 0 ) d^, где (A₁, A₂) - произвольное решение уравнений

2A( 0 ) A^ - A₂ = 0,2A( 0 ) A₂ ^ - A₁ = 0.

В частности, если взять A₁ = cos 0 , A₂ = -sin 0 , то опера-тор.А_н перейдет в оператор A_t = д _х, а если взять A₁ = sin 0 , A₂ = cos 0 , то оператор А_н перейдет в оператору = д , который, очевидно, допускается исходной системой. Симметрии 5₀ отвечает оператор растяжения

Х=х д _х + у д _у .

Для того чтобы записать операторы высших симметрии в исходной системе координат, необходимо представить оператор рекурсии

V = I D ^X

I 0

D x

в систему координат х, у. В результате получим новый оператор рекурсии:

, | ( к 0 -о ) D_x + ( к 0^^ ) D_v              0

—.        — l         у у X X X у

V: = I             0               (к0 -a,)D, + (к0 -о,)D„ yyx xxy

.

Окончательно получаем следующую теорему Теорема 2. Алгебра симметрий для уравнения (1) состоит из точечных симметрий, которые порождаются операторами

Х= Э_о ,Х_я = (h^os 9 - h₂sin 9 ) d _x + (h₁sin 9 - h₂cos 9 )d^, а также высшими симметриями, которые имеют вид с § ^,

( хо_х +уа где у -     '      ' .

I x9v+y9r I

Законы сохранения уравнения (5). Для построения законов сохранения уравнения (5) следует решить урав

нение

1р‘1=0,

„  7*

где I f =

D, — D

| ф ]

; g =l    , здесь о, r e 3 .

1ф I                  n

Отсюда следует, что необходимое условие выполнено только для четных n. Имеет место следующая теорема.

Теорема 3. Законы сохранения для уравнения (5) порождаются производящими функциями Т_2п,Е.

Производящей функции ( ф , г) отвечает сохраняющийся ток (- ф u + rv, ф и + rv). В интегральной форме закон сохранения имеет вид

J (-ф и + V v) dy + (фи + V v) dx = 0 г для всякого замкнутого контура Г в плоскости переменных (х,у).

Законы сохранения для уравнения (1). На основании предыдущего пункта имеет место следующая теорема.

Теорема 4. Класс производящих функций, порождающих законы сохранения уравнения (1), образуется как векторное пространство элементамиК^А, где K _{2 n} = Л ^{- 1} T _{2 n} ;

Без труда можно установить, что ф = Anu (n) + An-1 un-1 + ••• + m^

V=^- A n v ( „ ) + A n -1 V n -1 + ••• + m ² ,

I- sin 9 cos 9

N =Л^-1 E ; Л = 2Al

I cos 9 sin 9

•

гдеХ = const, (m1, m2) - произвольное решение системы уравнений m1 + m1 - fm2 = 0, m2 - m2 - f mx = 0.

xy     xy

Все решения уравнения

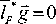
При этом закон сохранения в исходной системе координат в интегральной форме запишется как

[ ( -ф о+у9 )( о _х - k ( 9 ) 9 _х ) + ( ф а + ф9 )( а _х + k ( 9 ) 9 _х ) ] dx +

= 0,

Г +1 ( -фа + ф9 )( о y - k ( 9 ) 9 y ) + ( фо + ф9 )( о y + k ( 9 ) 9 y ) J dy где у- замкнутый контур в области изменения перемен-ных^у о , 9 - произвольное решение системы уравнений (1).

можно описать следующим образом:

т+е = v ^п ( Т о ) + Е ,

I и I где T₀ =1     ; E =

■ v

m m2

•

Теперь проверим выполнение необходимого условия

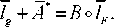
Нетрудно видеть, что Т ,Е удовлетворяют необходимому условию. Для функций Т имеем

1 = р -vnL =-VM,

1 о Uo)          1 о

A* = (-1) n Vn A,

где A =

I-1 0

10 1