Группировка объектов массива (по качеству действия)

Пояс астероидов — это область Солнечной системы, расположенная между орбитами Марса и Юпитера. В 19 веке обсуждалась дискуссия о том, что от Марса до Юпитера могла бы проходить орбита еще одной планеты.

Юпитер еще с давнего времени оказывал огромное влияние на область, лежавшую ближе к Солнцу. Он притягивал к себе часть вещества из этой зоны. Законы движения небесных тел, составляющих Солнечную систему, были установлены трудами Иоганна Кеплера. Они имеют только кинематический характер, другими словами они не рассматривают причины, обусловливающие движение планет.

Для примера, рассмотрим задачу Кеплера для трех тел. Тело массой m, в первоначальный момент времени находиться в точке с радиус вектором и имеет скорость. Притягивающие центры массами М1 и М2 находятся в точках с радиус векторами и , соответственно. Задача Кеплера состоит в необходимости определить траекторию движения тела в зависимости от его начальных координат, начальной скорости и кинетической энергии. На рисунке 1 показана траектория движения тел главного пояса.

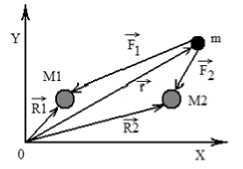
Рисунок 1 – Траектория движения тела

Для решения задачи используется алгоритм Верле в скоростной форме. С его помощью рассчитываются последующие значения координаты, скорости и ускорения материальной точки.

Преимущество скоростного алгоритма в том, что он является самостартующим и не приводит к накоплению погрешностей.

Орбиты астероидов располагаются в Главном поясе неравномерно. Вращаясь на этих орбитах вокруг Солнца, астероиды Главного пояса попадают в орбитальный резонанс относительно вращения Юпитера вокруг светила. Благодаря этому, Юпитер действует на них своей гравитацией, с одной и той же периодичностью. Другими словами, Юпитер «раскачивает» астероиды, искажая их орбиты. Это слабое влияние, но оно накапливается раз от раза. В результате, астероиды на этих орбитах либо сталкиваются со своими соседями и меняют орбиту, либо Юпитер их "выбрасывает" из Солнечной системы вообще. Образуются пустые орбиты, которые и назвали щелями Кирквуда.

Для исследования влияния планет было выбрано 500 астероидов для удобства отображения и восприятия, у каждого из них случайным образом формируется начальная координата и начальная скорость движения.

Для реализации работы использовалось программное обеспечение MATLAB. С помощью него возможно выполнение работы и демонстрирование результатов в одном и том же документе — на рабочей странице MATLAB. На рисунке 2 показаны щели «Кирквуда».

Рисунок 2 - Щели Кирквуда

По рисунку 2 видно, как астероиды двигались под воздействием Солнца. Можно отметить, что по мере отдаления от Солнца орбита астероидов всё больше похожа на окружность, а чем ближе к небесному светилу, тем орбита становится более эллиптической. На рисунке 3 показана система «Астероиды - Солнце».

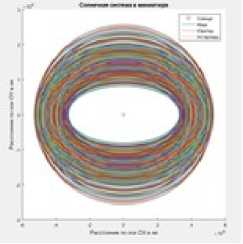
Рисунок 3 - Система Астероиды - Солнце

Далее добавим планету Солнечной системы - Марс.При добавлении нового небесного тела траектория главного полюса начала сплющиваться и вытягиваться вверх в данной системе координат. Черным цветом отмечена траектория движения Марса. На рисунке 4 показана система «Астероиды – Солнце - Марс».

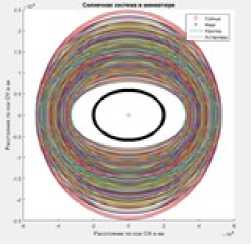
Рисунок 4 - Система Астероиды – Солнце - Марс

При добавлении Юпитера в данную систему траектория астероидов оказалась ещё более вытянутой и некоторые астероиды начинают выходить даже за орбиту Юпитера, что свидетельствует о стремлении астероида покинуть пределы солнечной системы.

Таким образом, в данной работе было проведено исследование движения астероидов главного пояса в поле тяжести таких планет, как Марс и Юпитер.Так же была построена гистограмма распределения астероидов по их орбитам, что в свою очередь подтверждает наличие явления «щели Кирквуда».