Хаотическая динамика гибких прямоугольных в плане панелей в поле белого шума
Автор: Крылова Е.Ю., Яковлева Т.В., Баженов В.Г.
Статья в выпуске: 1, 2016 года.
Бесплатный доступ
Исследуется влияние на характер колебаний гибкой прямоугольной в плане панели интенсивности внешнего поля белого шума, нормального к поверхности панели. Математическая модель колебаний панели построена на основании гипотез Кирхгофа с учетом диссипации. Геометрическая нелинейность учтена в форме Кармана. Рассматривается прямоугольная панель с отношением размеров в плане под действием внешней продольной нагрузки. К уравнениям движения присоединяются неоднородные граничные условия опирания на гибкие несжимаемые (нерастяжимые) ребра и нулевые начальные условия. Полученная система нелинейных дифференциальных уравнений в частных производных сводится к нелинейной системе обыкновенных дифференциальных уравнений методом конечных разностей по пространственным переменным. По времени система решается методом Рунге-Кутта четвертого порядка точности. Количество степеней свободы механической системы в эксперименте равняется 196. Для анализа получаемых результатов в работе, помимо Фурье-анализа, применяется аппарат вейвлет-преобразований, что позволяет более детально изучить локальные временные особенности сигналов. Эксперимент выявил диапазон амплитуд внешней продольной нагрузки, где поведение рассматриваемой динамической системы не устойчиво. Для данного диапазона амплитуд продольной нагрузки было проведено исследование влияния поля белого шума различной интенсивности на характер колебаний панели. Проведенные численные эксперименты показывают, что поле белого шума способно уменьшать амплитуду колебаний панели, сокращать количество частот в спектре колебаний системы и переводить несимметричные формы колебаний к симметричным. Таким образом, можно утверждать, что воздействие на динамическую систему шумовым полем может приводить к более безопасным колебательным режимам. То есть с помощью белого шума можно управлять характером колебаний механической системы.
Нелинейная динамика, параметрические колебания, диссипативные системы, панели, хаотические колебания, белый шум, вейвлет-анализ, фурье-анализ, управление колебаниями
Короткий адрес: https://sciup.org/146211604
IDR: 146211604 | УДК: 539.3:534.1 | DOI: 10.15593/perm.mech/2016.1.06
Текст научной статьи Хаотическая динамика гибких прямоугольных в плане панелей в поле белого шума
PNRPU MECHANICS BULLETIN
Исследуется влияние на характер колебаний гибкой прямоугольной в плане панели интенсивности внешнего поля белого шума, нормального к поверхности панели. Математическая модель колебаний панели построена на основании гипотез Кирхгофа с учетом диссипации. Геометрическая нелинейность учтена в форме Кармана.
Рассматривается прямоугольная панель с отношением размеров в плане λ = 4 под действием внешней продольной нагрузки. К уравнениям движения присоединяются неоднородные граничные условия опирания на гибкие несжимаемые (нерастяжимые) ребра и нулевые начальные условия. Полученная система нелинейных дифференциальных уравнений в частных производных сводится к нелинейной системе обыкновенных дифференциальных уравнений методом конечных разностей по пространственным переменным. По времени система решается методом Рунге-Кутта четвертого порядка точности. Количество степеней свободы механической системы в эксперименте равняется 196. Для анализа получаемых результатов в работе, помимо Фурье-анализа, применяется аппарат вейвлет-преобразований, что позволяет более детально изучить локальные временные особенности сигналов. Эксперимент выявил диапазон амплитуд внешней продольной нагрузки, где поведение рассматриваемой динамической системы не устойчиво. Для данного диапазона амплитуд продольной нагрузки было проведено исследование влияния поля белого шума различной интенсивности на характер колебаний панели. Проведенные численные эксперименты показывают, что поле белого шума способно уменьшать амплитуду колебаний панели, сокращать количество частот в спектре колебаний системы и переводить несимметричные формы колебаний к симметричным. Таким образом, можно утверждать, что воздействие на динамическую систему шумовым полем может приводить к более безопасным колебательным режимам. То есть с помощью белого шума можно управлять характером колебаний механической системы.
CHAOTIC DYNAMICS OF FLEXIBLE RECTANGULAR PANELSIN WHITE NOISE FIELD
E.Y. Krylova, T.V. Yakovleva, V.G. Bazhenov
NIIM Nizhny Novgorod State University N.I. Lobachevsky, Nizhny Novgorod, Russian Federation
|
ARTICLE INFO |
ABSTRACT |
|
Received: 9 February 2016 Accepted: 18 March 2016 Published: 30 March 2016 |
The paper studies the impact of a flexible rectangular panel intensity of the external white noise field (which is normal to the panel surface) on the nature of oscillations. A mathematical model of panel oscillations is based on Kirchhoff hypotheses with dissipation. The geometric nonlinearity is taken into account in the form of Karman. We consider |
|
Keywords: nonlinear dynamics, parametric oscillations, dissipative systems, panels, chaotic oscillations, white noise, wavelet analysis, Fourier analysis, control of oscillations |
|
|
1 a rectangular panel with an aspect ratio λ = 4 in plan, by an external longitudinal load. Equations of motion are joined by inhomogeneous boundary conditions of bearing on |
|
|
flexible incompressible (inextensible) edges and zero initial conditions. The resulting system of nonlinear differential equations in private derivatives is reduced to a nonlinear system of ordinary differential equations by the method of finite differences in spatial variables. As for the time, the system is solved by the Runge-Kutta fourth-order accuracy. The number of degrees of freedom of the mechanical system in the experiment equals to 196. In order to analyze the results obtained in the work, in addition to the Fourier analysis, the authors applied the wavelet transformation unit, which allows a more detailed study of the local time signal features. The experiment has revealed a range of amplitudes outer longitudinal load, where the behavior of the dynamical system is not sustainable. For this range of amplitudes of longitudinal load we studied the influence of the white noise field with varying intensity on the nature of the panel vibrations. The numerical experiments show that the white noise field is capable of reducing the amplitude of the oscillation panel, reducing the number of frequencies in the vibration spectrum of the system and transfering to the asymmetric waveform symmetry. So, it is possible to state that effecting the dynamic system with noise field can lead to safer vibrational modes. That is, using the white noise can be controlled by the nature of vibrations of the mechanical system. |
|
Прямоугольные в плане панели в качестве элементов конструкций находят широчайшее применение в различных областях техники: авиастроении, космической промышленности, судостроении, строительстве, приборостроении и др. Элементы подобных конструкций находятся под действием внешнего динамического давления различного вида и работают в средах с переменными во времени свойствами (случайные ударные воздействия, звуковое давление). Поэтому возникает необходимость комплексного исследования поведения таких систем. Для современного строительства важнейшим аспектом является установление множества параметров воздействия, которые будут характеризовать безопасный и опасный режимы работы элементов ответственных конструкций.
Для моделирования случайных во времени свойств внешней среды хорошо подходит белый шум. Как известно, поведение нелинейных динамических систем серьезно реагирует на малейшие изменения начальных условий, что может быть связано в том числе с влиянием шумовых полей.
Несмотря на более чем полувековую историю, вопросы моделирования сложной динамики механических систем остаются актуальными [1–6]. Однако влияние шумовых полей на сложные колебания механических систем мало изучено. Показано, что случайные воздействия играют весьма существенную роль в поведении динамических систем в таких областях, как физика, химия, биология [7]. Для динамических систем с одной степенью свободы установлено, то внешние шумы способны вызывать качественную перестройку колебательных режимов системы [8–10]. В работах F. Jinqing, Zhao De-min, Gan
Chaunbiao, Manohar C.S., и других серьезное внимание уделяется теоретическим исследования уравнений типа Дуффинга с учетом внешних шумов [11]. В статье В.Д. Потапова показано, что неустойчивая по Ляпунову детерминированная параметрическая система может быть стабилизирована путем наложения на параметрическую нагрузку случайного шума [12]. Статья [13] посвящена влиянию шума на контактное взаимодействие пластины, подкрепленной ребрами жесткости. В работе [14] излагаются результаты опытного изучения балочно-ударной системы при возмущениях типа гауссова шума. Показано, что при учете нескольких форм колебаний реакция нелинейной модели сильно отличается от реакции расчетной модели с одной степенью свободы. В статье [15] также показано, что учет количества степеней свободы существенно влияет на достоверность получаемых результатов.
Данная работа посвящена исследованию влияния поля белого шума на нелинейную динамику гибких прямоугольных в плане панелей под действием внешней продольной нагрузки. Вопрос влияния шумовой составляющей на характер колебаний рассматриваемых панелей особенно интересен и важен, так как его касаются впервые и нигде в литературе ранее он освещен не был.
Математическая модель колебаний прямоугольной в плане панели основывается на гипотезах Кирхгофа. Геометрическая нелинейность учитывается в форме Т. Кармана [16].
В прямоугольной системе координат трехмерная область имеет вид: Ω= { x 1 , x 2 , x 3 | ( x 1 , x 2 ) ∈ [0; a ] × [0; b ], x 3 ∈ [ -δ ; δ ]} (рис. 1).
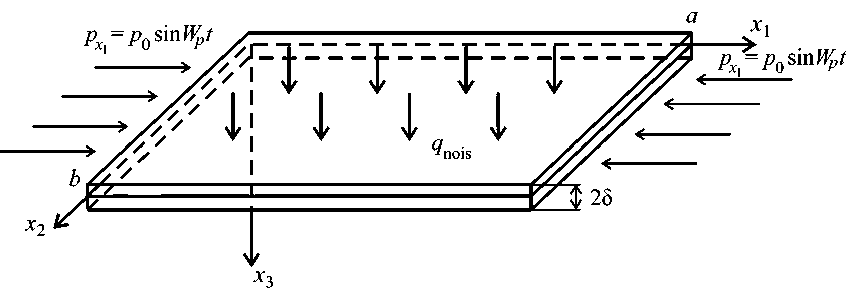
Рис. 1. Схема приложения нагрузки и шумового поля к пластине
Математическая модель колебаний панели описывается системой нелинейных дифференциальных уравнений в частных производных, записанных в безразмерном виде [17]:
12(1 -µ 2 )
( ∇λ 4 w ) - L ( w , F )
-
∂ 2 w
∂ t 2
-
∂ w ε
∂ t
- qnois = 0,
∇λ 4 F + 1 2 L ( w , w ) = 0,
∂2w∂2F ∂2w∂2F ∂2w ∂2F где L(w,F)= + -2 ; L(w,w) – известные нелинейные опера-
∂ x 1 2 ∂ x 2 2 ∂ x 2 2 ∂ x 1 2 ∂ x 1 ∂ x 2 ∂ x 1 ∂ x 2
1 ∂ 4 ∂ 4 ∂ 4
торы; ∇= +λ + 2 , w и F – функция прогиба и усилия соответст-
λ λ 2 ∂ x 1 4 ∂ x 2 4 ∂ x 1 2 ∂ x 2 2
венно; µ – коэффициент Пуассона; γ – удельный вес материала пластины; E – модуль
Юнга материала пластины; g - ускорение свободного падения; Х = a/b, где a,b - размеры пластины в плане по x1 и по x2 соответственно. Система (1) приведена к безразмер- ному виду с использованием следующих безразмерных параметров: x1 = axi, x2 = bx2 - безразмерные параметры пластины по x1 и по x2 соответственно; w = 25w; F = E(25)3 F ;
a t = tot - время, t0 = —, K = K
Eg
\ Y
;
£ = (2 5 ) г - коэффициент демпфирования среды; q nois -
внешний белый шум. Черточка над безразмерными параметрами в уравнениях (1) для простоты опущена. К уравнениям (1) присоединяются граничные и начальные условия в зависимости от типа нагружения и закрепления пластины.
Методы решения
Система (1) с учетом граничных и начальных условий сводится к нелинейной системе обыкновенных дифференциальных уравнений (СОДУ) методом конечных разностей с аппроксимацией O ( с 2) по пространственным переменным. Первое уравнение нелинейной СОДУ по времени решается методом Рунге-Кутта 4-го порядка относительно функции прогиба. Выбор метода обоснован в статье [18]. Далее значения функции прогиба подставляются в правую часть второго уравнения системы. Второе уравнение системы (1) становится линейным и решается методом обратной матрицы относительно функции усилия на каждом шаге по времени. Число разбиений в методе конечных разностей n x n = 14 x 14. Выбор количества разбиений МКР и обоснование достоверности получаемых результатов приведены в работе [19]. Применение метода конечных разностей позволяет рассматривать пластину как систему с большим числом степеней свободы, в данном численном эксперименте их число 196 (14×14).
Для глубокого понимания поведения динамических систем под действием той или иной нагрузки необходима информация, скрытая в частотной области сигнала. Получаемые в результате исследований динамики нелинейных пластин сигналы зачастую имеют сложную структуру по временной оси. Поэтому в работе применялся аппарат вейвлет-преобразований. Основным преимуществом вейвлет-анализа перед Фурье является возможность отследить локализованные особенности нестационарного сигнала. В то время как в коэффициентах Фурье отражается поведение сигнала на всем временном интервале. Если с помощью Фурье-анализа рассматривать сигнал, частотные характеристики которого существенно меняются с течением времени, то на выходе будем иметь «сумму всех его поведений», наложенных друг на друга. Вейвлет спектр сигнала, в свою очередь, серьезно зависит от материнского вейвлета, на основании которого он строится. В работе [19] приведено обоснование выбора в качестве материнского вейвлета Gauss32, который дает лучшую локализацию по частоте по сравнению с ранее используемым вейвлетом Morlet. Следует отметить, что как бы ни была хороша локализация вейвлета по оси частот, на вейвлет-спектре хорошо различимы только первые три-четыре бифуркации системы. Если в спектре колебаний присутствует частота, амплитуда которой значительно превосходит амплитуду другой частоты, то на вейвлет-спектре последняя будет плохо различима. Фурье-спектр дает возможность видеть гораздо большее количество бифуркаций системы, регистрирует все, даже незначительные, движения частот и визуализирует частоты вне зависимости от их амплитуды.
Поэтому при исследовании нелинейной динамики распределенных механических систем следует применять Фурье- и вейвлет-анализ совместно, опираясь на сильные стороны каждого из них.
Численные эксперименты, проведенные в работе, направлены на изучение влияния интенсивности внешнего шумового поля, нормального к поверхности пластины, на характер колебаний рассматриваемой динамической системы. Продольная нагрузка задавалась в виде pX 1 = p 0sin to pt , где to p , p 0 - частота и амплитуда внешнего воздействия соответственно. Колебания рассматривались на временном интервале t е [0,286]. Коэффициент диссипации среды а = 1, ц = 0,3. Частота продольной нагрузки to p = 6,4, что превосходит частоту собственных колебаний системы. Отношение размеров панели 1 в плане х —.
К системе (1) присоединялись неоднородные граничные условия опирания на гибкие несжимаемые (нерастяжимые) ребра [20]
a2 w a2 f w = 0; —= 0; F = 0; —= 0 при x = 0; 1, 221
oX 1 d X i
w = 0; V = 0; F = 0; = px при x 2 = 0; 1
22 x 2
ОX 2 d X 2 1
и нулевые начальные условия
w ( x i , x 2 >l t =0 = 0, I w = 0. о t
Аддитивный шум добавлен в систему в форме случайного слагаемого с постоянной интенсивностью q oisn = q n 0 (2,0*rand()/(RAND_MAX + 1,0) - 1,0), где q n 0 - интенсивность шума; rand() – стандартная функция языка C++, принимающая случайное целое число от 0 до RAND_MAX, RAND_MAX – константа, равная 65535. Выражение (2,0*rand()/(RAND_MAX + 1,0) - 1,0) принимает произвольные дробные значения в диапазоне (–1;1). Данная математическая модель белого шума предложена Perry R. Cook и Gary P. Scavone (Центр компьютерных исследовании в области музыки и акустики (CCRMA) Стэндфордского университета).
В рамках численного эксперимента были получены две последовательные бифуркации удвоения периода колебаний рассматриваемой динамической системы. После чего система резко переходила к хаосу. В работе [21] показано, что для динамических систем в виде прямоугольных в плане пластин первая бифуркация зачастую является бифуркацией Андронова–Хопфа. Следует отметить, что пластина в рассматриваемом случае (в диапазоне амплитуд нагрузки 82,6 < p0 < 105) очень резко реагирует на малейшее изменение нагрузки. Так, двухчастотные колебания (p 0 = 82,611) сменяются хаотическими (p0 = 82,612) при изменении значения амплитуды нагрузки на 0,001 %. Дальнейший рост управляющего параметра на 0,001 приводит колебания системы к двухчастотным (p0 = 82,613). Как видно из табл. 1, хаотические колебания системы при фиксированной амплитуде продольной нагрузки меняют свой характер с течением времени. Есть окна, где доминирует частота возбуждающей силы top, и области, где преобладает частота top /2 ((p0 = 82,612, p0 = 82,618). Из последней строки табл. 1 видно, что окна хаоса могут меняться областями с одной или двумя бифуркациями Хопфа. В табл. 1 вейвлет-спектры построены на основании материнского вейвлета Gauss 32, ось ординат – частота, ось абсцисс – время.
Таблица 1
Вейвлет- и Фурье-спектры q nois 0 = 0, p 0 е [82,611,82,635]
p о = 82,611
p 0 = 82,612
Вейвлет-спектры
p 0 = 82,613
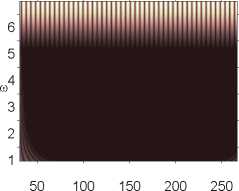
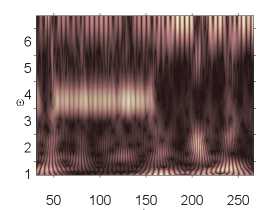
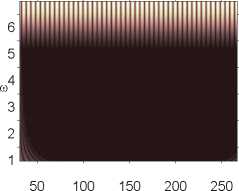
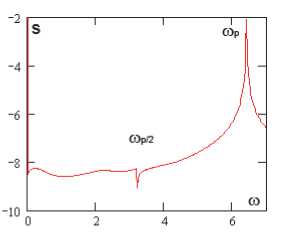
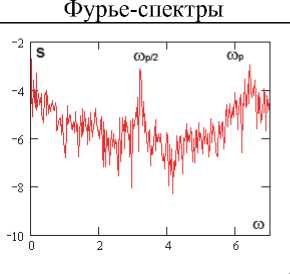
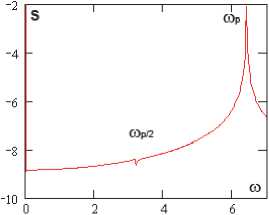
p о = 82,617
p 0 = 82,618
p 0 = 82,619
Вейвлет-спектры
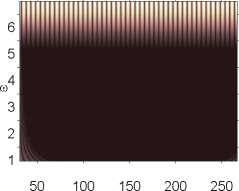
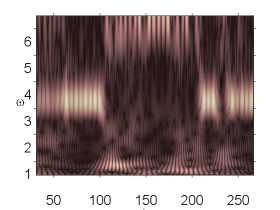
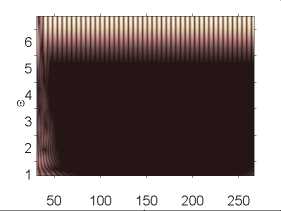
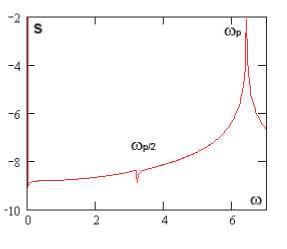
Фурье-спектры
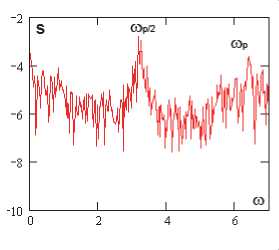
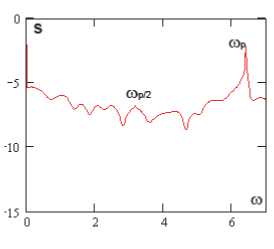
p 0 = 82,629
p 0 = 82,630
p 0 = 82,632
Окончание табл. 1
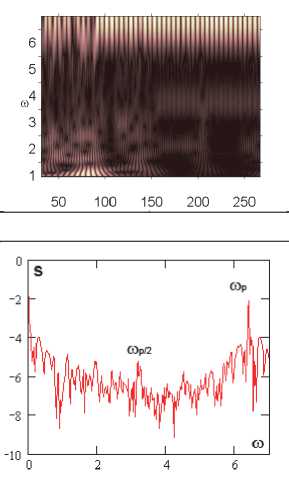
Вейвлет-спектры
6 5
>4
lllllllllllllllllllllllllllllllllllllllllllllll
50 100 150 200 250
Фурье-спектры
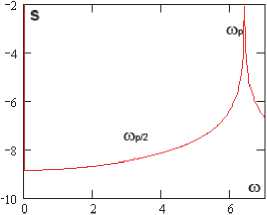
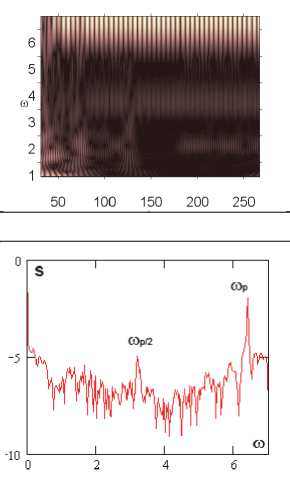
Анализ влияния внешнего, нормального белого шума на колебания системы проводился в том диапазоне амплитуд внешних продольных нагрузок, где система сильно неустойчива p 0 g [82,611,82,635] (табл. 2). Интенсивность белого шума в эксперименте бралась следующим образом: q nois0 g [1,30]. Были построены сигналы с шагом по амплитуде продольной нагрузки 0,001. Выявлено, что влияние внешнего шума интенсивности qnois 0 g [1,5] ухудшало состояние системы, при q nois 0 = 5 все сигналы были хаотическими. В диапазоне qnois 0 g [10,30] система становилась менее чувствительной к шумовому воздействию. Отдельно стоит отметить qnois 0 = 15, в данном случае наблюдалось улучшение состояния системы по сравнению с qnois 0 = 0 в диапазоне амплитуды продольной силы p 0 g [82,616, 82,635]. Интенсивность внешнего шума q nois 0 = 10,20,25 улучшала состояние системы в диапазоне p 0 g [82,628,82,634].
Таблица 2
Влияние интенсивности поля белого шума на характер колебаний пластины p0 g 82,628 p0 g 82,629 p0 g 82,631
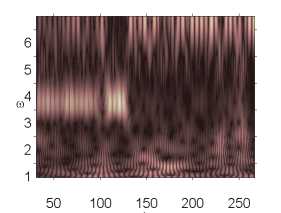
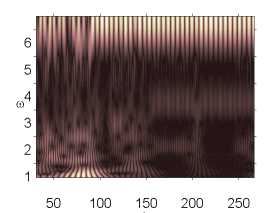
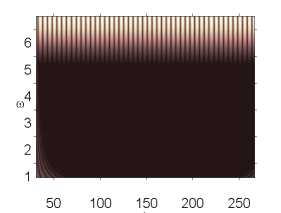
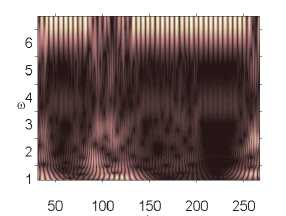
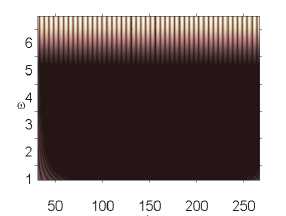
Окончание табл. 2
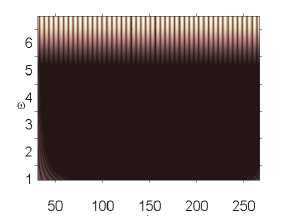
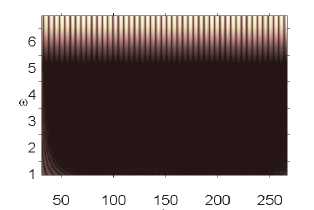
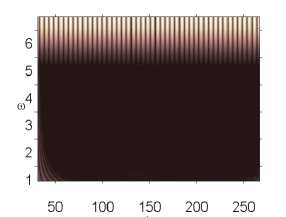
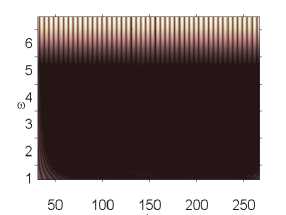
p 0 e 82,632 p 0 e 82,633 p 0 e 82,635
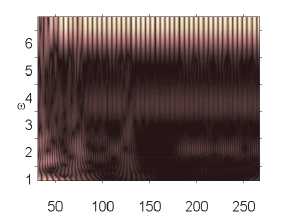
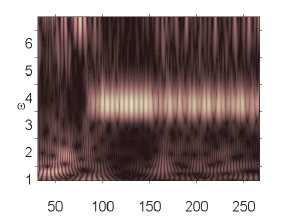
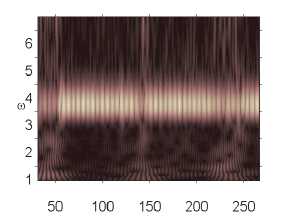
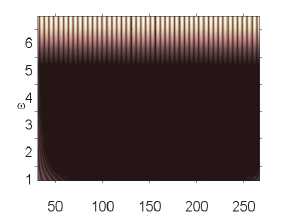
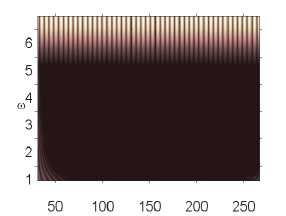
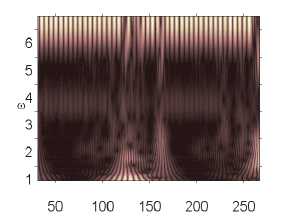
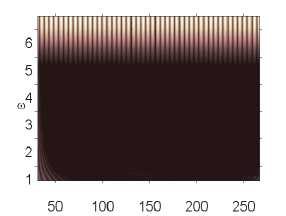
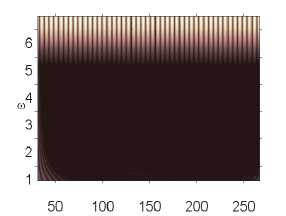
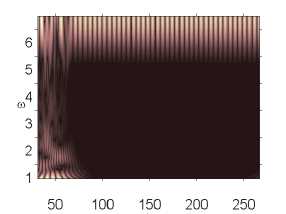
Численный эксперимент показал, что амплитуда и характер сигналов совпадают там, где колебания системы в шумовом поле и без него отличны от хаотических. Шум интенсивности q nois о = 15 снижал амплитуду сигнала в области хаотических колебаний (рис. 2).
Проводился анализ влияния интенсивности шумового поля, нормального к плоскости панели, на форму ее колебаний. В случае амплитуды внешней продольной нагрузки p 0 = 82,629 на всем временном интервале были получены несимметричные формы колебаний. Наложение шумового поля интенсивности q nois 0 = 10 уменьшало степень несим-метрии форм панели. В эксперименте с полем белого шума интенсивности q nois 0 = 15 ( p 0 = 82,629) несимметричных форм колебаний не обнаружено (табл. 3).
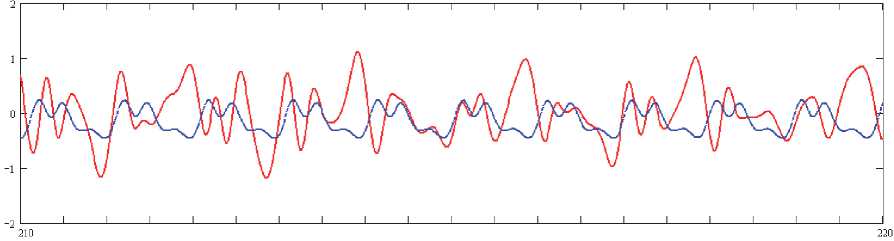
Рис. 2. Сигналы при амплитуде продольной нагрузки p 0 = 82,635, q nois 0 = 0 и qnois 0 = 15
Таблица 3
Поверхности панели при p 0 = 82,629, t % 100
q nois 0 = 0
q nois 0 = 15
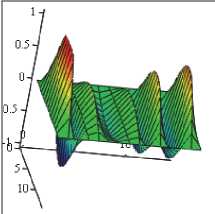
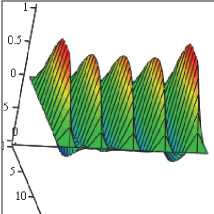
Проведенные численные эксперименты показывают, что поле белого шума способно уменьшать амплитуду колебаний панели, сокращать количество частот в спектре колебаний системы и переводить несимметричные формы колебаний к симметрии. Таким образом, можно утверждать, что воздействие на динамическую систему шумовым полем может приводить к более безопасным колебательным режимам. То есть с помощью белого шума можно управлять характером колебаний механической системы.
Работа выполнена при финансовой поддержке РНФ (грант №15-19-10039)
Список литературы Хаотическая динамика гибких прямоугольных в плане панелей в поле белого шума
- Кузнецов С.П. Динамический хаос. -М.: Физматлит, 2006. -356 с.
- Хаотическая динамика гибких прямоугольных в плане пластин при действии продольных нагрузок/Е.Ю. Крылова, Т.В. Яковлева, И.В. Папкова, В.А. Крысько//Проблемы прочности и пластичности: межвуз. сб. -Н. Новгород: Изд-во Нижегород. гос. ун-та, 2015. -Т. 77, № 3. -С. 235-243.
- Кузнецов А.П., Савин А.В., Тюрюкина Л.В., Введение в физику нелинейных отображений. -Саратов: Научная книга, 2010. -134 с.
- Коган Е.А., Юрченко А.А. Нелинейные колебания трехслойных и многослойных пластин и оболочек при периодических воздействиях (обзор)//Изв. Моск. гос. техн. ун-та. -2014. -Т. 4, № 1 (19). -С. 55-70.
- Spatio-temporal nonlinear dynamics and chaos in plates and shells/J. Awrejcewicz, V.A. Krysko, I.V. Papkova, E.Yu. Krylova, A.V. Krysko//Nonlinear Studies. -2014. -Vol. 21. -Iss. 2. -No. 2. -P. 313-327.
- Крысько В.А., Крылова Е.Ю., Папкова И.В. Нелинейная динамика параметрических колебаний двухслойных распределенных систем с учетом зазора между слоями//Вестн. Сарат. гос. техн. ун-та. -2013. -Т. 1, № 1 (69). -С. 7-11.
- Хорстхемке В., Лефевр Р. Индуцированные шумом переходы: Теория и применение в физике, химии и биологии: пер. с англ. -М.: Мир, 1987. -400 с.
- Слепнев А.В., Вадивасова Т.Е., Листов А.С. Мультистабильность, удвоения периода и подавление бегущих волн шумовым воздействием в нелинейной автоколебательной среде с периодическими граничными условиями//Нелинейная динамика. -2010. -Т. 6, № 4. -С. 755-767.
- Слепнев А.В., Вадивасова Т.Е. Бифуркации удвоения периода и эффекты шумового воздействия в мультистабильной автоколебательной среде//Прикладная нелинейная динамика. -2011. -Т. 19, № 4. -С. 53-67.
- Жогаль С.П., Жогаль С.И., Сафонов И.В. Применение метода канонических разложений при исследовании амплитуды установившихся колебаний в системах с одной степенью свободы//Изв. Гомель. гос. ун-та. -2006. -№ 4. -С. 105-109.
- Feng Jinqing, Xu Wei, Wang Rui Stochastic responses of vibro-impact Duffing oscillator excited by additive Gaussian noise//J. Sound and Vibr. -2008. -Vol. 309. -No. 3-5. -С. 730-738.
- Потапов В.Д. Об устойчивости стохастических вязкоупругих систем//Пробл. машиностр. и надеж. машин. -2009. -№ 6. -С. 85-90.
- Контактное взаимодействие пластины с системой балок при наличии зазоров с учетом белого шума/Т.В. Яковлева, В.Г. Баженов, В.А. Крысько, Е.Ю. Крылова//Вестник Пермского национального исследовательского политехнического университета. Механика. -2015. -№ 4. -С. 259-272. DOI: DOI: 10.15593/perm.mech/2015.4.15
- Non-linear dynamics of a stochastically excited beam system with impact Int./N. van de Wouw, A. de Kraker, D.H. van Campen, H. Nijmeijer//J. Non-Linear Mech. -2003. -Vol. 38. -No. 5. -P. 767-779.
- Awrejcewicz J., Krylova E.Y., Krysko V.A. Regular and chaotic dynamics of flexible plates//Proceedings of the International Conference on Structural Engineering Dynamics (ICEDyn 2013). -Portugal, Sesimbra, 2013. -10 p.
- Karman Th. Festigkeitsprobleme in Maschinenbau//Encykle. D. Math. Wiss. -1910. -Vol. 4. -No. 4. -P. 311-385.
- Вольмир А.С. Нелинейная динамика пластинок и оболочек. -М.: Наука, 1972. -432 с.
- Routes to chaos in continuous mechanical systems. Part 1: Mathematical models and solution methods/J. Awrejcewicz, V.A. Krysko, I.V. Papkova, A.V. Krysko//Chaos Solitons & Fractals. -2012. -Vol. 45. -P. 687-708.
- Wavelet-based analysis of the regular and chaotic dynamics of rectangular flexible plates subjected to shear-harmonic loading/J. Awrejcewicz, E.Y. Krylova, I.V. Papkova, V.A. Krysko//Shock and vibration. -2012. -Vol. 19. -P. 979-994
- Корнишин М.С. Нелинейные задачи теории пластин и пологих оболочек и методы их решения. -М.: Наука, 1964. -192 с.
- Regular and chaotic dynamics of flexible plates/J. Awrejcewicz, E.Yu. Krylova, I.V. Papkova, V.A. Krysko//Shock and Vibration. -2014. -8 p. -ID 937967.


