Хаотические колебания космического аппарата с упругим вертикальным тросом

сила натяжения троса мала по сравнению с гравитационной силой, поэтому ее влияние будем учитывать только при рассмотрении движение КА вокруг центра масс. Трос будем представлять как невесомый упругий стержень, длина которого изменяется согласно закону Гука. Масса КА существенно превышает массу концевого груза. Центр масс КА движется по круговой орбите. В плоскости орбиты введем систему координат Ox ₁ y ₁ , в которой ось Ox ₁ совпадает с местной вертикалью, и связанную со спутником систему координат Oxyz , в которой плоскость Oxy совпадает с плоскостью орбиты, ось Ox направлена по продольной оси КА. Запишем уравнения движения КА относительно центра масс в проекции на ось Oz , перпендикулярную плоскости движения Oxy (на рис. 1 орбита показана штриховой линией), в виде [5]:

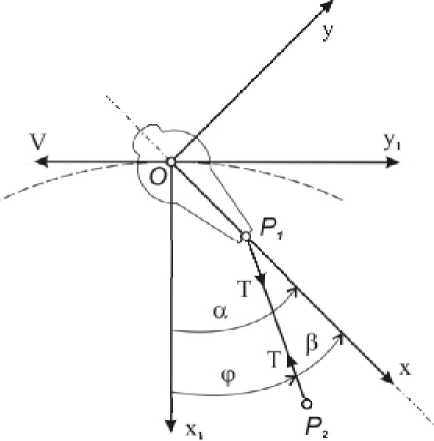
Рис. 1. КА с тросовой системой

C a = - 3 цр³ (B - A )sin a cos a - T A sin( a - ф ), (1) где a — угол между продольной осью тела и местной вертикалью, ф - угол между линией действия силы натяжения троса и местной вертикалью, A ,B ,C – главные компоненты тензора инерции тела в связанной системе координат Oxyz , T – величина силы натяжения троса, A = OP 1 (рис. 1), Ц - гравитационная постоянная, p - параметр орбиты, в = a - ф .

Движение концевого груза относительно КА описывается следующими уравнениями в полярных координатах [1]:

ф + to + 2r-1 r(

Трос будем представлять как невесомый упругий стержень, длина которого изменяется согласно закону Гука:

T = E (rl-1 - 1), (5) где E – модуль упругости, l – длина ненапряженного троса. Пусть груз движется строго по местной вертикали в окрестности положения равновесия (4). Тогда уравнение (3) с учетом (5) примет вид r + О2 r = Em -1. (6) где О2 = Em 11 1 - 3to2 > 0 (для материалов, применяемых для космических тросовых систем [1]). Равновесное положение груза определяется формулой r0 = E (E - 3 mto21)-11.

При начальных условиях: t0 = 0: r = r0, r = V0, решение уравнения (6) имеет вид r = r0 + V0О-1 sin Оt, (7)

Для того чтобы трос находился в растянутом положении, начальная скорость груза при прохождении положения равновесия не должно превышать следующего значения

V ₀ <  3 to ² m ^1/2 1 ^3/2 ( E - 3 m to ² 1 ) ^{- 1} /2 .

Сила натяжения троса согласно (5) и (7) изменяется по гармоническому закону

T = T 0 + T m sin О t , (8)

где T 0 = 3 m to ² 1E ( E - 3 m to ² 1 ) , T m = V ₀ Em ^1/2 1 ^{- 1/2} ( E - 3 to ² ml ) - 1/2 .

БИФУРКАЦИОННЫЙ АНАЛИЗ И СЕПАРАТРИСНЫЕ РЕШЕНИЯ

Будем рассматривать движение КА относительно центра масс с развернутым по местной вертикали тросом, тогда уравнение (1) с учетом (8) примет вид a = - a sin a - c sin a cos a - £ sin a sin О t, (9)

A T B - A 3 ц    A T где a = —°, c = -— --£, £ = -m.    (10)

C Cp C

При малом положительном параметре £ , уравнение (9) можно к классу квазиконсерватив-ных с малым периодическим внешним возбуждением. Невозмущенное движение ( £ = 0 ) отвечает условию (4) и описывается уравнением:

a = - a sin a - c sin a cos a . (11)

В силу (10) коэффициент a >  0 всегда больше нуля, а знак коэффициента c зависит от соотношения моментов инерции A и B . Положения равновесия невозмущенной системы (11)

определяются как корни уравнения sin a (1 + у cos a )= 0 , (12) где у = ca-1. Из (12) следует, что два положения равновесия отвечают значениям: a* = 0, п, а третье положение равновесия: a* е (0, п) существует, при условии:

I Y >  1 . (13)

Если это условие не выполняется, то наблюдается только два положения равновесия, причем центр всегда находится в точке a * = 0 , а седло в точке - a * = п .

Очевидно, что для у < -1 точки a* = 0, п являются седлами, а промежуточная точка a = ± arccos (-у 1) - центром (левая ветвь диаграммы на рис.2). Если у > 1, то наблюдается обратная картина (правая ветвь диаграммы на рис. 2). Отметим, что бифуркационная диаграмма (рис. 2) для отрицательных углов a получается зеркальным отображением относительно оси абсцисс. Гиперболические точки существуют, когда выполняется условие (13). В этом случае периодическое внешнее возмущение £sin a sin Оt в возмущенной системе (9) может стать причиной хаоса [6].

Для исследования поведения динамической системы (9) в окрестности сепаратрис воспользуемся методом Мельникова [7], который позволяет найти толщину хаотического слоя и пересечение устойчивых и неустойчивых многообразий. Для применения метода Мельникова требуется получить аналитические выражения для сепаратисных орбит, другими словами, найти решения уравнения невозмущенного движе-

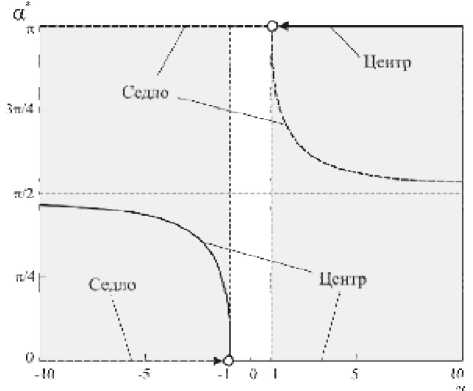
Рис. 2. Бифуркационная диаграмма невозмущенной системы (11)

ния на сепаратрисах. Вид решений зависит от величины параметра у = ca -1 и начальных условий движения. Будем рассматривать два случая, определяющих величину параметра у .

Случай 1. Пусть параметр у = ca-1 > 1,(14)

тогда седло aS = ± arccos (-у-1)

лежит между значениями 0 , п (рис. 2), а в точках аС = 0, ± п -(16)

имеются центры. Отметим, что центр а С = - п совпадает с центром а С = п . При а ^ - п и при а ^ п скорости а совпадают, поэтому можно утверждать, что фазовые траектории замкнуты на цилиндрическом фазовом пространстве. Будем рассматривать эволюцию фазовых траекторий на цилиндрическом пространстве для а е [ - п , п ] . Выделим две области A 0 и A 1 , разделенные двумя седлами 5 1 и 5 - 1 (рис. 3). Необходимо отметить, что область A ₁ “разрезана” по вертикали а = п , - п . Из (15) следует, что седло 5 1 принадлежит интервалу a _S е ( п /2, п ) и при у ^ го a _S ^ п /2 .

Уравнение (11) имеет интеграл энергии

2 а ² + W ( а ) = E ,         (17)

с 2

где W(а) = -a cos а - 2 cos а - потенциальная энергия, E – полная энергия.

Если полная энергия E > WS, где WS = W(os ) , тогда система совершает вращение в одной из внешних областей. Если E < WS , то в зависимости от начальных условий наблюдаются колебания в одной из внутренних областей. При равенстве E = WS движение происходит по гетероклиническим траекториям, которые соединяют гиперболические точки 51 и 5-1.

Сначала рассмотрим область A0 (рис. 3). Найдем решение уравнения (11) на сепаратрисах (гетероклинические траектории). Разделим переменные в интеграле энергии (17), тогда получим da

t=г а 0

2[ W ( o _s ) + a cos а + 2cos ² а ] ’ ⁽¹⁸⁾

где W ( o _s ) = - a cos a _S

—cos2 а = — . Замены 2S2c переменных:

x=tana/2

в интеграле (18) и последующее интегрирование приводит к следующим гетероклиническим траекториям [8]

I аX а, (t) = ±2 arctan tan -tanh ±                   I 22

X sin а

Ст± (t) = (O' )±=±            S (20)

cosh X t + cos o _s ’

X = ( c ² - a ² ) 1 ^/2 c

-

где

-1/2               ____________________

1/2 – действительное число при выполнении условия (14).

Для области A ₁ гетероклинические траектории имеют аналогичный вид [8]

а , ( t ) = п ± 2 arctan cot ° S- tanh —