Хаотический анализ движения космического аппарата с малой массовой асимметрией при спуске в атмосфере
Автор: Асланов В.С., Ледков А.С.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Механика и машиностроение
Статья в выпуске: 3-1 т.11, 2009 года.
Бесплатный доступ
Методами хаотической динамики исследовано неуправляемое движение космического аппарата с малой массовой асимметрией при спуске в атмосфере. На космический аппарат действует восстанавливаемый момент, описываемый бигармонической зависимостью. С помощью метода Мельникова исследовано поведение системы в окрестности сепаратрисы. Получены аналитические решения движения космического аппарат по гомоклиническим траекториям. Найдены критерии возникновения хаоса и представлены результаты численного моделирования, подтверждающие справедливость полученных решений. Исследовано изменение толщины хаотического слоя в процессе спуска космического аппарата в атмосфере. Даны рекомендации по выбору уровня демпфирования, устраняющего возможность появления хаотических переходов на всей траектории спуска
Космический аппарат, бигармонический момент, хаос, метод мельникова, гомоклиническая траектория, аналитическое решение, хаотический слой, устойчивость, сечения пуанкаре
Короткий адрес: https://sciup.org/148198583
IDR: 148198583 | УДК: 629.78
Текст научной статьи Хаотический анализ движения космического аппарата с малой массовой асимметрией при спуске в атмосфере
т а = a sin а + b sin2 a . (1)
Поскольку устойчивыми будут два положения равновесия а = 0 и а = п , в процессе спуска КА его пространственный угол атаки может принимать как малые, так и большие значения. Это делает невозможным применение метода линеаризации. Для исследования движения КА необходим анализ нелинейных дифференциальных уравнений. В частном случае движения осесимметричного КА, когда состояние системы определяется изменением одной быстрой переменной - пространственного угла атаки, получены приближенные аналитические решения нелинейной возмущенной системы[5]. В случае движения КА с малой асимметрией система уравнений становится двухчастотной. При этом создаются предпосылки для возникновения различных видов параметрических резонансов. Нелинейный анализ резонансов строится, как правило, на использовании аналитических решений невозмущенного движения[6]. Эти решения имеют весьма сложный вид, что затрудняет их применение.
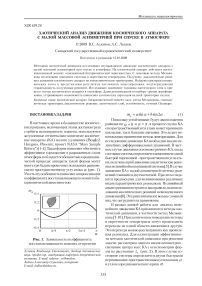
В рамках данной работы для анализа нелинейного движения КА применяются методы хаотической динамики, в частности метод Мельникова [7-10]. При хаотическом поведении системы в окрестности сепаратрисы могут происходить переходы из одной области движения в другую. Эти переходы можно рассматривать как проявления резонанса. Для иллюстрации эффективности методов хаотической динамики при решении задачи, рассмотрим один из видов асимметрии -смещение центра масс КА с оси симметрии формы на расстояние zT (рис. 2). В этом случае состояние системы определяется двумя быстрыми переменными: пространственным углом атаки а и углом аэродинамического крена ф .
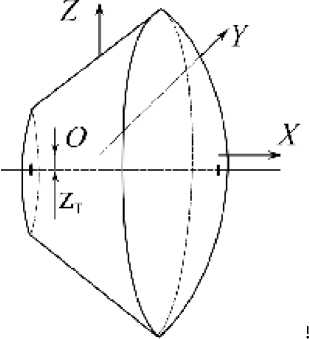
Рис. 2. Космический аппарат
НЕЛИНЕЙНАЯ СИСТЕМА
силы c ya ( а ) по углу атаки, m KA - масса КА, z — { R ,G , V , H ,0} - вектор медленных переменных, 0 - угол наклона траектории.
Коэффициент ст разложим в ряд Фурье и ограничимся рассмотрением нескольких первых членов ст — c0 + c1cos а + c2 cos 2а. (5)
Будем также считать, что коэффициент D постоянен.
При е = 0 система (1)-(3) приводится к невозмущенной:
(R - G cos а) ( G - R cos а'
а +( ) - М а — 0 . (6)
sin а
Уравнение (6) имеет аналитическое решение, форма которого зависит вида от корней полинома
Запишем систему дифференциальных уравнений, описывающую движение КА с малой асимметрией ( zT Ф 0 ) относительно его центра масс О при спуске в атмосфере [6]
2 aSL bSL 2
f ( и ) — 2(1 — u )( h--qu--qu ) +
II (7)
+ 2 GRu - G 2 - R 2,
( R - G cos а )( G - R cos а )
sin3 а — Е Ф а ( а , ф , z ),
— М а
где h – энергия системы. В случае, когда все корни полинома f ( u ) действительны ( u 1 , u 2 , u 3 , u 4 ) и пронумерованы так, что u 1 > u 2 , u 3 > u 4 , а u 3 < u 2 или u 4 > u 1 , решение имеет вид [6]:
ф = — R -Ix
G - R cos а
2 , sin а ,
z — г Ф2 ( а , ф , z );
qS а qSL .
еФ„ — D - zTc sin ф, а у T Т I
qSL
Ма — —та ,
d — mic
^^^^^^^в
са ya
ImKA
Здесь R и G – с точностью до множителя проекции вектора кинетического момента на продольную ось и на направление скорости, V – скорость движения центра масс КА, D – коэффициент демпфирования, q — р (H)V 2 / 2 - скоростной напор, р (H ) - плотность атмосферы, H - высота полета, S – площадь миделевого сечения КА, L - характерный размер КА, Ix , I – продольный и по-
перечный моменты инерции КА, m znz
5 mzn д® п
компоненты матрицы производных аэродинамических коэффициентов по безразмерным угловым скоростям, заданных в системе координат, связанной с пространственным углом атаки, tozn — iznL / V, izn — проекция угловой скорости на ось z , та - коэффициент восстанавливающе-а го аэродинамического момента, cya – производная коэффициента аэродинамической подъемной
u i ( u 2 — u з ) + u з ( u i — u 2 ) cos y cos а — - —— ( u 2 - u 3 ) + ( u 1 - u 2 ) cos Y
где y — am( P t + т о , k ) ,
qSL ( u i — u з )( u 2 — u 4 )
N 2 1
, (8)
k—
,
( u i — u 2 )( u 3 — u 4 )
( u i — u 3 )( u 2 — u 4 )
т 0 - постоянная интег-
рирования. В случае, когда полином f ( u ) имеет как действительные u i , u 2 ( u i > u 2 ), так и мнимые u 34 ± iv корни,
cos а —
a 2
где § a , a i
(u2 + ui§) - (u2 - ui§) cos y
( i + § ) - ( i - § ) cos Y ’ (9)
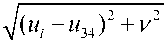
,
_ = I qSLai a2 k — 2 - ( u i -^X u - u 34) + ^ 2
2 I , 2 2 a 1 a 2 .
Здесь и всюду далее i — i, 2 .
УРАВНЕНИЯ ГОМОКЛИНИЧЕСКИХ
ТРАЕКТОРИЙ
Для использовании метода Мельникова [7-10] необходимо найти гомоклинические траекторий а 0 i ( t ) невозмущенной системы (6) (рис. 3).
Рис. 3. Фазовый портрет невозмущенной системы
p = f p + E g p , а = Л + е д а ;
f p =
( R - G cos а )( G - R cos а )
I sin3 а
- qSL ( a sin а + b sin 2 а ) ,
Движению по сепаратрисе соответствует *
энергия, вычисленная в седловой точке а 0
gp = zT ( c 0 + c 1 cos а + c 2 cos 2 а ) qSL sin ф -
- D^ ,
V
(G-Rcosa0) qSL , , „ h = ------2—+--(a cos а0 + b cos2 а0).
2sin а0 Iх ’
Полином f ( u ) при этом имеет четыре действительных корня, два из которых совпадают u 1 = u 4 = u 0 . Перенумеруем корни:
а.) u 1 = v 0 , u 2 = v 1 , u 3 = v 2 , u 4 = v 0 ; (10)
b.) u 1 = v 0 , u 2 = v 2 , u 3 = v 1 , u 4 = v 0 . (11)
Вариант (a) соответствует траектории а01, а вариант (b) - траектории а02. Подставляя корни (10) и (11) в решение (8) и учитывая, что cos у = cn(Pt + т0,1) = ch-1 (Pt + т0).
f = Р а
J а i , да = 0 ;
где p = I а - обобщенный импульс. Величины q и V , G и R будем считать постоянными, а в качестве закона изменения угла аэродинамического крена - использовать зависимость ф = Xt, где X - осредненная по периоду колебания угла атаки угловая скорость
T
X =1 T
7 J
I ( G - R cos а ) cos а
— R --2-----
I x sin а
dt =
где Р -
qS L ( v о - v 2)( v o - v i )
2 I
cn - эллипти-
ческий косинус [11]; получим уравнения гомоклинических траекторий в виде
cos а 0 ( t ) = v j +-- 0---- j---------
1 + v °Z v L ch -2 ( e t + т 0 ) , (12)
Vi - v j
0 = f (cos a i 0( t ))"
1 ^1 - cos2 а ”( t ) . (13)
Здесь траектории а 01 соответствует значение j = 2 , а траектории а 0 2 - j = 1 .
ОЦЕНКА УСТОЙЧИВОСТИ ОБЛАСТЕЙ ДВИЖЕНИЯ
Переменные z медленно меняются в процессе спуска КА. Однако они не являются периодическими по времени величинами, поэтому применение описанного в [9, 10] модифицированного метода Мельникова для систем с медленными параметрами невозможно.
Рассмотрим возмущенную систему, получаемую из (2)-(4) при фиксации некоторого момента времени.
о.....
а тах
= 2 f IR -
TI а тт V x
( G - R cos а ) cos а ^ d а
min
= R --1
V I x )
-
sin2 а
2 ( GJ 1 - RJ 2 )
T
_ ^ max cos а d а
J 1 = sin а а
min
;
а тах
Jг = J min
d а
- • 2 :
а sin а 1
а тах
T = 2 d ^
а & .
min
Для вычисления интегралов (16) необходимо представить функцию (7) в виде f ( u ) = ^q^^ ( u - u 1 )( u - u 2)( u - u 3)( u - u 4 ) для случая, когда f ( u ) имеет только действительные корни; либо в виде f ( u ) = ^q^^ ( u - u 1 )( u - u 2) ( ( u - u 34)2 + V 2 )
для случая, когда присутствуют комплексные корни. Воспользовавшись заменой u = cos а и выражениями (8) или (9), перейдем в интегралах (16) от переменной а к переменной Y . Пос-
ле алгебраических преобразований подынтегральных выражений, (16) сводятся к полным нормальным эллиптическим интегралам Лежандра первого K ( к ) и третьего П ( n , к ) рода [11]
где g p ( a 0 ( t ), t + 1 ° ) – вектор возмущений, вы численный на -ой гомоклинической траекто
-
-
рии. Подставляя в (17) f и g из (14), получим
J 1 = в ( C 1 П ( n 1 , к ) + C 2 П ( n 2 , к ) + C 3 K ( к ) ) ,
Mi ■ ( t ° ) = J qSLzT a 0 ( t ) sin ( ^ ( t + 1 ° ) ) x
x ( c ° + c 1 cos a ° ( t ) + c 2 cos 2 a ° ( t ) ) -
J 2 = в ( с 1 п ( n 1 , к ) - с 2 п ( n 2 , к ) + с 4 к ( к ) ) ,
n qSi°( t )2
D V
. (18)
d t .
п где K (к) = J
d y
1 - к 2 sin2 у
п
П ( n - к ) = i;-------- 2 dY 2 ■ 2 .
о ( 1 + n sin y ) \1 - к sin Y
В случае, когда все корни (7) действительные
T _ 2 K (к) C _ и 2 - и з в ; 1 2(1 - и 2)(1 - из) ’
C 2 =
U 2 — U 3
2(1 + и 2)(1 + и 3 )
u 3
C 3 1.2
1 - и 3
Здесь a ° ( t ) и a ”( t ) вычисляются по формулам (12), (13) соответственно.
Если функция Мельникова Mi ( t 0) имеет простой корень в точке t 0 , то при достаточно малом £ устойчивые и неустойчивые многообразия пересекаются трансверсально. Если функция Mi ( t 0) не имеет простых корней, то устойчивые и неустойчивые многообразия не пересекаются и хаотических режимов, обусловленных пересечением гомоклинических структур не возникает. Другими словами критерий Мельникова позволяет судить об устойчивости областей движения системы (14). В случае, если функция Мельникова имеет простые корни, то в системе присутствует хаос и фазовая траектория может пересечь сепаратрису и покинуть свою область.
C 2
C 4
с _ —1—
4 1 - и 3 2 ’
n _ ( и 2 - и 1)(1 - и 3 )
1 ( и 1 - и 3)(1 - и 2 ) ’
ХАОТИЧЕСКИЙ АНАЛИЗ
n _ ( и 2 - и 1)(1 + и 3 )
( и 1 - и 3)( 1 + и 2 ) '
Для случая комплексных корней
T _ 4 к ( к ) с _ их - и 2 X - Х 3
в ’ 2(1 — и 1 )(1 — и 2 ) X 2 — X 4 ,
и — и 2 X + X 3
2(1 + и )(1 + и 2 ) X 2 + X 4
C 3 _
2 x 2 x 4
X 2 — X 4
2 x 2 2
X 2 — X 4
n 1 =
( X 2 - X 4 )
4 a 1 а 2 (1 - и 1 )(1 - и 2)
( X 2 + X 4 ) 2
n 2 _ 7 , X = ад + а ,
4 а 1 а 2(1 + и 1 )(1 + и 2) 1 1 2
X 2 = а 1 — а 2 , X 3 = и 2 а 1 + и 1 а 2 , X 4 = и 2 а 1 - и 1 а 2 .
Запишем критерий Мельникова [10] для системы (14).
Mi ( t 0 ) = Л f a ( а 0‘ ( t ) ) g p ( “ ^ ( t ), t + t ° ) -
- fp ( « ° / ( t ) ) g a ( «° i( t ), t + t 0 ) d t , (17)
Рассмотрим движение КА, имеющего следующие массово-геометрические параметры: L _ °.35 м, S _ 2.8 м3 , IX = 1 кг • м 2 , I = 3 кг • м 2 , zT = °.°2 м. Аэродинамические коэффициенты КА зададим с помощью выражений (4) и (5), в которых а _ Q.Q36 , b _- Q,178 c ° = °.°69 , c 1 = 1.112 , c 2 = °.2°6 (рис. 1). Построим критерий Мельникова (18) для системы (14), имеющей следующее параметры R = °.5c — 1 , G = °.2c — 1 , X = 2 c — 1 , V _ 1°°° м/ с, q = 2°°° кг/мс2 .
При D _ ° M 1 и M 2 обращаются в ноль в нескольких точках. В этом случае в системе возникает хаос. При D _ °.°5 M 2 не обращается в ноль, то есть в окрестности второй гомоклинической траектории хаоса не возникает (рис. 4). На рис. 5, 6 показаны сечения Пуанкаре, построенные для фазовых траекторий, начинающихся только в областях A 1 и A 2 . Область A 2 устойчива: фазовые траектории, начинающиеся внутри этой области, не покидают ее (рис. 5). Область A 1 неустойчива (подвержена хаосу): некоторые фазовые траектории, начинающиеся в этой области, пересекают сепаратрису и попадают в другие области движения (рис. 6). При D _ °.6 ни M 1 ни M 2 не обращаются в 0 и в окрестности гомоклинических траекторий хаоса не возникает, то есть обе области устойчивы.
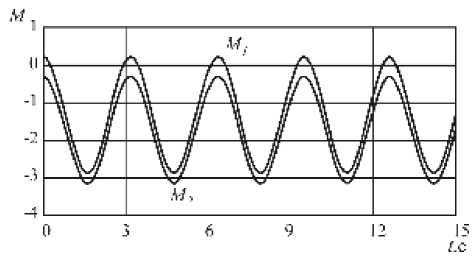
Рис. 4. Критерий Мельникова для областей A 1 и A 2 , вычисленный при D = 0.05
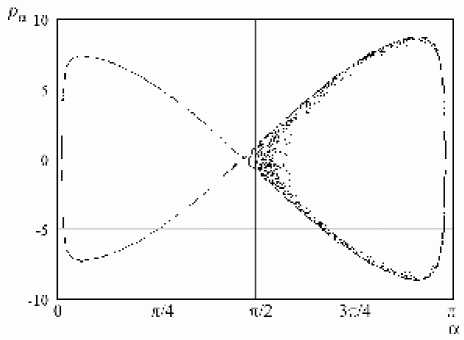
Рис. 5. Сечение Пуанкаре для фазовых траекторий, начинающихся в области A 2 при D = 0.05
Поскольку хаотический анализ выполнялся для фиксированного момента времени, следует определить точку на траектории спуска, в которой КА наиболее подвержен хаосу. Критерий Мельникова Mi ( t 0) характеризует толщину хаотического слоя в окрестности сепаратрисы [10]. Изучим, как меняется толщина этого слоя в процессе спуска КА. Пусть рассмотренный ранее КА осуществляет спуск в атмосферу Марса [12] при следующих начальных условиях: а 0 = п /6 , а = 0 c - 1 , V0 = 1000 м/с , H0 = 120 км , 0 0 = — п /12 . Зададим коэффициент демпфирования D = 0.01 . В качестве приближенной характеристики толщины хаотического слоя будем рассматривать величину
A i = max M i ( t 0) — min M i ( t 0) .
На рис. 7 показано изменение A i в процессе спуска. Максимальная толщина хаотического слоя наблюдается при максимальном значении скоростного напора (при t = t * рис. 8). Выбирая коэффициент демпфирования D достаточно большим для подавления хаоса при t = t * , мы тем самым устраним его на всей траектории спуска. Значение параметров системы в момент t = t * можно получить, рассмотрев движение центра масс КА при спуске в атмосфере без учета движения относительно центра масс.
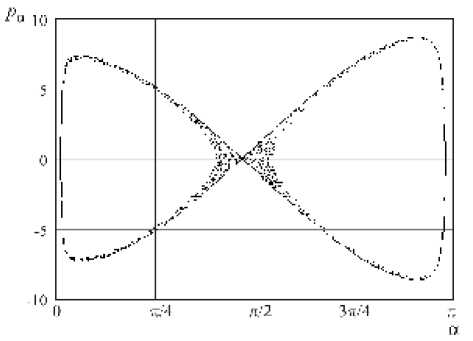
Рис. 6. Сечение Пуанкаре для фазовых траекторий, начинающихся в области A 1 при D = 0.05
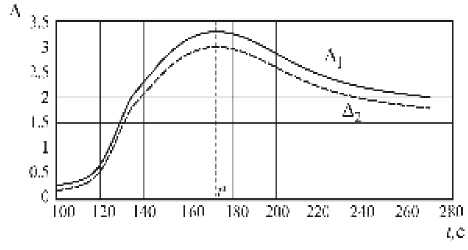
Рис. 7. Изменение толщины хаотического слоя в процессе спуска
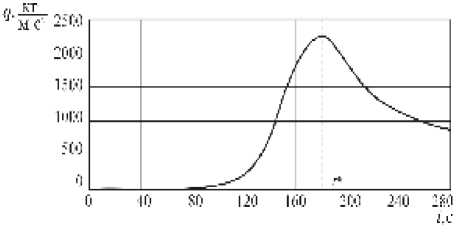
Рис. 8. Изменение скоростного напора при неуправляемом спуске КА
ЗАКЛЮЧЕНИЕ
В работе предложен новый, основанный на методах хаотической динамики, подход к исследованию пространственного движения КА с малой асимметрией при спуске в атмосферу. Получены уравнения гомоклинических траекторий нелинейной системы дифференциальных уравнений движения КА. На основании метода Мельникова записан критерий устойчивости движения в окрестности гомоклинических траекторий. Исследовано изменение толщины хаотического слоя в процессе спуска КА в атмосфере и даны рекомендации по выбору уровня демпфирования, устраняющего возможность появления ха- отических переходов на всей траектории спуска. Несмотря на то, что в работе рассматривался лишь один из видов асимметрии, предложенный подход может быть легко распространен и на другие ее виды.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (0601-00355).
Список литературы Хаотический анализ движения космического аппарата с малой массовой асимметрией при спуске в атмосфере
- Sancisi-Frey S., Spry J.A., Garry J., Pillinger J.M. Atmospheric entry simulations of Mars lander bioload -experiments in support of Beagle 2//Research in Microbiology. 2006. Vol. 157. pp. 25-29.
- Gershman R., Adams M., Mattingly R., Rohatgi N., Corliss J., Dillman R., Fragola J., Minarick J. Planetary protection for Mars sample return//Advances in Space Research. 2004. Vol. 34. pp. 2328-2337.
- Collinet J., Brenner P., PalermS. Dynamic stability of the HUYGENS probe at Mach 2.5//Aerospace Science and Technology. 2007. №11 pp. 202-210.
- Shotwell R. Phoenix-the first Mars Scout mission//Acta Astronautica. 2005. Vol. 57. pp. 121-134.
- Асланов В.С., Ледков А.С. Особенности вращательного движения КА при спуске в атмосфере Марса//Космические исследования. 2007. Т 45, № 4 С. 351-357.
- Асланов В.С. Пространственное движение тела при спуске в атмосфере. М.: Физматлит, 2004. 160 с.
- Wiggins S, Holmes P. Homoclinic orbits in slowly varying oscillators//SIAM J. Math. Anal. 1987. Vol. 18. № 3. pp. 612-629.
- Holmes P. and Marsden J. Horseshoes in perturbations of hamiltonian systems with two degrees of freedom//Commun. Math. Phys. 1982. Vol. 82. pp 523-544.
- Faouzi Lakrad, Moulay Mustapha Charafi Perturbation methods and the Melnikov functions for slowly varying oscillators//Chaos, Solitons and Fractals. 2005. Vol. 25. pp. 675-680.
- Симиу Э. Хаотические переходы в детерминированных и стохастических системах. Применение метода Мельникова в технике, физике и нейрофизиологии. -М.:ФИЗМАТЛИТ, 2007. -208с.
- Янке Е., Эмде Ф., Леш Ф. Специальные функции (формулы, графики, таблицы). М.: Наука, 1968. 344с.
- Мороз Б.И, Кержанович В.В, Краснопольский В.А Инженерная модель атмосферы Марса для проекта Марс-94 (МА-90)//Космич. исслед. 1991. Т. 29. № 1. С. 3-19.