Характер изменения национального дохода в модели гармонического осциллятора при линейной зависимости внешних инвестиций от времени

Исследования экономических процессов методами, применяемыми при решении физических задач, начались с середины 1990ых годов. В научной литературе появилось много работ (см., например, [1-3] и приведенный там список литературы), в которых авторы стараются экономические задачи различного характера решить, используя теорию и методы, разработанные физиками для решения задач в области физики. Работа [4] посвящена применению методов статистической физики к экономическим системам (в частности, для описания финансовых систем). Авторы работы [5] считают возможным экономический закон спроса и предложения объяснить с помощью физического закона сохранения матери и энергии. В работе [6] автором предложены теоретико-методологические основы физической экономики. Приведены определения скорости, силы, энергии, ускорения в экономике. Работы [7-8] посвящены исследованию динамики изменения национального дохода в модели гармонического осциллятора с возмущением без учета трансакционных издержек (затухание отсутствует) и с учетом последних (затухание присутствует). В настоящей работе решается аналогичная задача в предположении, что внешние инвестиции линейно зависят от времени.

Целью исследования является анализ динамики изменения национального дохода в зависимости от времени в предположении, что национальный доход удовлетворяет обыкновенному дифференциальному уравнению гармонического осциллятора с правой частью.

Постановка задачи и ее решение

Пусть национальный доход как функция от времени (Y(t)) удовлетворяет дифферен- циальному уравнению гармонического осциллятора с внешним воздействием (внешние инвестиции) без учета трансакционных издержек (коэффициент затухания η = 0). Предполагая, что внешние инвестиции в зависимости от времени меняются по линейному закону, получим, что Y(t) удовлетворяет следующему обыкновенному неоднородному дифференциальному уравнению с постоянными коэффициентами второго порядка d2Y t

—^+ -^У ( t ) - —•t,       (1)

где первый член уравнения d ² Y ( t )/ dt ² – темп изменения национального дохода, второй член m² ₀ Y ( t ) — рыночная сила, го 0 - собственная частота осциллятора, βt – внешние инвестиции, β > 0 – темп роста инвестиций.

Если при решении уравнения (1) пользоваться методом Эйлера и методом вариации произвольных постоянных [9], то для определения неизвестных функций c ₁( t ) и c ₂( t ), входящих в следующее выражение частного решения неоднородного уравнения (1)

• ^Y_ ( t ) c i ( t ) cos ( ® 0 t ) ⁺ c 2 ( t ) sin ( ^to0 t ) , ⁽²⁾

получим систему уравнений

<

dc. ( t )       , d   dC) ( t )       , .

---— • cos (^t) + —2^- • sin (aM) = 0, dt         ^{(   0} ) dt         ^{(   0} )

-

dc ,( t )          / \ dc. ( t )          / \

----— • ro ₀ sin ( ro ₀ t ) + —2 -^ • to ₀ cos ( ro ₀ t ) = —t.

dt                  dt

Решение (3) имеет вид:

c i ⁽ t ) = -^2 ® 0

• t • cos ( a>_ot ) -

--sin

к

® 0

in ( ® 0 t ) ,

в I            1    /xl

^C2 ( t ) = — • t • sin ( ® 0 t ) ⁺--cos ( ® 0 t )

® 0 к            ® 0         7

Как известно [12]

Y o н ( t ) = Y ( t ) = Y o о ( t ) + Y ч н ( t ),       (6)

где Y ( t ) = Y_{o н} ( t ) – общее решение неоднородного уравнения (1), Y_{o о} ( t ) – общее решение соответствующего однородного уравнения, Y_{ч н} ( t ) – одно частное решение неоднородного уравнения (1). Из (6) с учетом (2), (4), (5) и того факта, что

Yoo (t) = c1cos(ro0t) + c2sin(ro0t), где c1 и c2 – произвольные постоянные, получим

Y ( t ) = c ₁ cos ( m ₀ t ) + c ₂ sin (a> ₀ t ) +— • t . (7) ® 0

Коэффициенты c ₁ и c ₂ в (7) находятся из начальных условий Коши

Y(t)| =0,dY ( t^ ^{( л} t= ⁰        dt

=0

и имеют вид c₁ = 0, c₂-- — / to 0 .       (9)

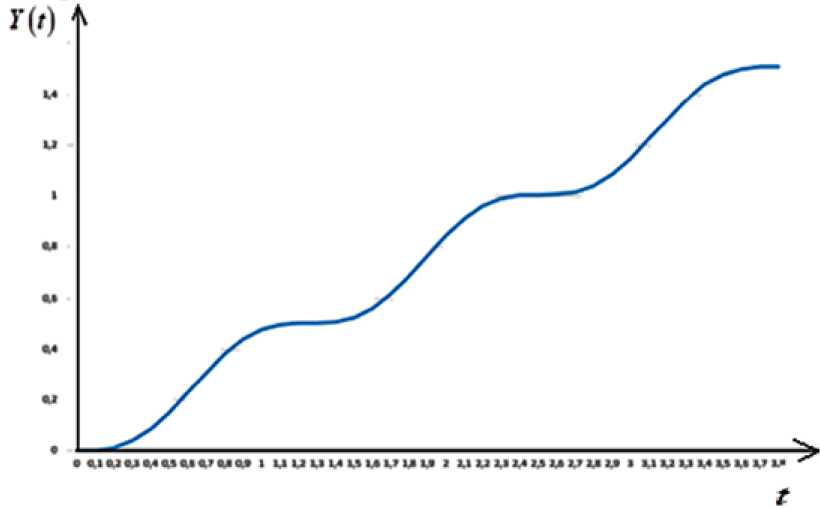
Рис. 1. Зависимость национального дохода от времени согласно (10) при η = 0; ω0 = 5; β = 2; 0 ≤ t ≤ 3,8

Подставляя (9) в (7), для Y(t) получим выражение

в (    1     / X

Y ( t ) =--t--sin ( m₀t )

®0 (   ®0

Теперь перейдем к рассмотрению случая, когда не пренебрегаем трансакционными издержками (η ≠ 0). Тогда функция Y(t) будет удовлетворять следующе- му неоднородному дифференциальному уравнению d2Yt    dYt

—+¹ + 2^(1 + toY ( t ) = p-1. (11) dt          dt

Решение соответствующего однородного уравнения, найденного методом Эйлера ( Y ( t ) = е ^λt , λ – характеристические числа), приводит к следующим результатам:

• а) . При ⁿ = to² ₀, 2 1 = ^ 2 = -n = to . _aY_o . _o . ( t ) = ( c^t ) e " .                          ⁽¹²⁾

• б) . При p2 > ю^,2, —^ + n22 - to2,22   q -^rj-^D,,

  Y.At ) = ( =e+= 2 =" ) - e"”.

  
  
  
  

• в) . При n 2 <  ® 0 . 2 1 = —n + i•>]to 0 - n 2 . 2 2 = —n - i^« 0 - П 2 .

  ^Yo.o. ( t ) = ( ^c1 COs ( уЯГ

  
  

  П 2 -1 ) + c ₂ sin

  
  
  
  
  

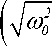
  n

  
  

  - 1

  
  

  e

  
  

  -n t

  
  
  
  

Отметим, что в (12), (13) и (14) c ₁ и c ₂ – произвольные положительные постоянные.

Для нахождения одного частного решения уравнения (11) (Yч.н.(t)) в случаях а)., б)., в). будем пользоваться методом подбора. Заметим, что этот метод применим, если правая часть неоднородного дифференциального уравнения имеет вид f (t) = ept (Pn (t) cos (qt) + Qm (t) sin (qt)), где n = m или n ≠ m.

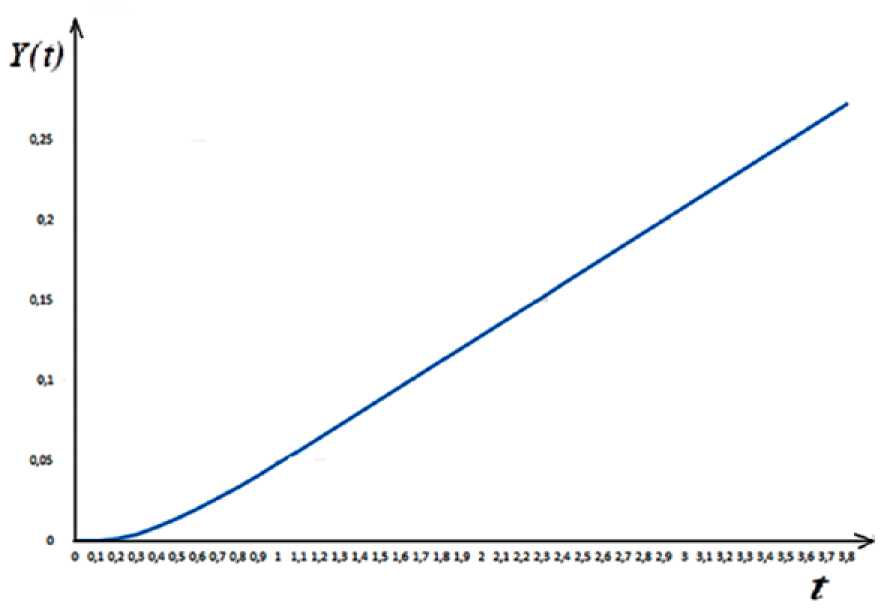
Рис. 2. Зависимость национального дохода от времени согласно (19) при η = ω0 = 5; β = 2; 0 ≤ t ≤ 3,8

а). Так как p + iq = 0 ≠ –η = –ω ₀, то Y_ч.н. ( t ) ищем в виде

Определяя c ₁ и c ₂ из начальных условий

Коши (8) и подставляя в (18), получим

Y_ч.н. ( t ) = A ∙ t + B ,             (16)

где неизвестные коэффициенты A и B найдем, требуя, чтобы (16) удовлетворяло уравнению (11). Вычисления приводят

Y ( t ) = в?

“ o

-      I              -

— + t e “ ^ot +t--

V “ o    )         “ o

. (19)

к следующему:

A ^в ,B = “ o

„3 ,    „2

“ o      “ o V

- I

— . (17)

“ n /

Тогда общее решение уравнения (11)

Y ( t ), согласно (6), имеет вид

Y ( t ) = ( c , +c - t ) e-“ °

+ 77 t “

—

2 В I — . (18)

“)

б). Так как p + iq = 0 Ф X12 = -± ^n- — “-,

то одно частное решение неоднородного уравнения (11) ищем в виде

Y_ч.н. ( t ) = C ∙ t + D , (20) где C и D пока неизвестные коэффициенты. Выражения для C и D найдем, требуя, чтобы (20) удовлетворяло уравнению (11). Вычисления приводят к следующим значениям

C = в ,D = - 2n- ^7.(21)

“o

Тогда общее решение неоднородного уравнения (11) примет вид

Y (t) = c1 ■ en++n--“-1't + c2 ■ e"n—^--“-'t + в ■ t — 2n •в.(22)

“o

После определения c ₁ и c ₂ из начальных условий Коши (см., (8)) (22) приобретает вид

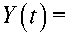
в2 л) П - «0 • «О

• e

(«2 - 242 - 2xj^2 - «0) • e^п «0 t +

+ ( 2^² — « 2 +6 ^П Л^{2 -} « 2 ) • e ^^Л « ⁰ t +-^- • t у

V                         ) J «о V «о)

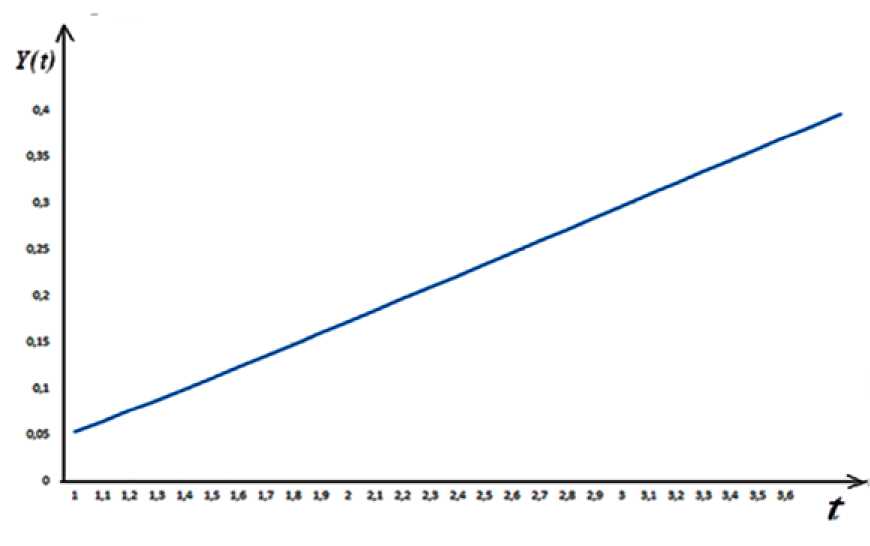
Рис. 3. Зависимость национального дохода от времени согласно (23) при η = 5; ω0 = 4; β = 2; 1 ≤ t ≤ 3,8

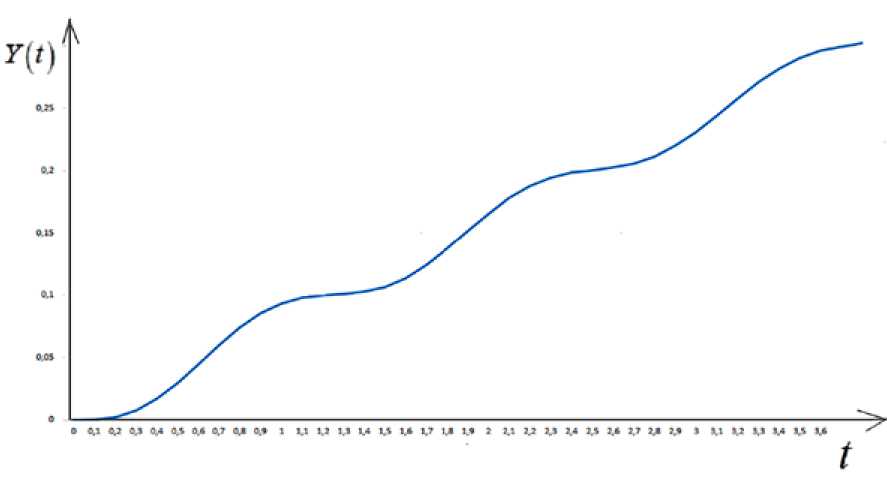
Рис. 4. Зависимость национального дохода от времени согласно (27) при η = 0,1; ω0 = 5; β = 2; 0 ≤ t ≤ 3,8

в). Так как p + iq = 0 ^ Х₁₅--П± i\П - « о , то аналогично случаю б). получим

Тогда Y ( t ) будет иметь вид

Y^. t ) = 4 •( t - « 0 I

)

«0 J

Y ( t ) = ( c i • cos « 0 ^— n²

• t + c₂ • sin J«_t

—

П 2 • t )

\

• e-^nt + ^e • t « 0 I

-

2n

« 0 J

Находя c ₁ и c ₂ из начальных условий Коши (см., (8)), для Y ( t ) в этом случае окончательно имеем

Y ( t )

в «0

2n

—cos

( «о

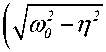
• t)

+

2n — «0

—

n2

sin

• t ) .

e ⁿ

+ t —

2n

« 0

Отметим, что на рисунках 1–4 приведены графики зависимости национального дохода от времени при различных значениях параметров, характеризующих динамику изменения национального дохода в модели гармонического осциллятора, когда внешние инвестиции линейно зависят от времени. Они построены согласно формулам (10), (19), (23) и (27). Рисунки 1 и 4 показывают, что при η = 0 (не учитываем трансакционные издержки) и η < 1 (трансакционные издержки малы), национальный доход в зависимости от времени возрастает, сохраняя колебательный характер. А в случае, когда коэффициент затухания η и частота собственных колебаний осциллятора ω ₀ величины одного порядка (см., рисунки 2 и 3), то национальный до-

ход в зависимости от времени возрастает по закону линейной функции.

Заключение

В работе исследована зависимость национального дохода от времени в физической модели гармонического осциллятора с внешним воздействием (внешние инвестиции) без учета и с учетом трансакционных издержек. При этом считается, что внешние инвестиции зависят от времени по линейному закону. Графический анализ, проведенный на основе полученных аналитических результатов, показывает, что национальный доход является возрастающей функцией в зависимости от времени. При этом характер возрастания зависит от значений параметров, входящих в выражение, определяющего национальный доход.