Характеристики радиального газостатического подшипника ступенчатого типа

В практике применения газостатических подшипников в металлорежущих станках обычно используют конструкции, в которых несущая способность создается за счет применения

дросселей. Такие подшипники имеют относительно низкую податливость, однако сложны в изготовлении. Альтернативой являются ступенчатые подшипники, которые хотя и имеют несколько б о льшую податливость, отличаются простотой конструкций и технологичностью [1].

В статье приведены результаты расчета и исследования статических и динамических характеристик ступенчатого газостатического подшипника, полученные на основе применения численно-аналитической методики, позволяющей выполнить их расчет с требуемой точностью.

Постановка задачи и метод ее решения

На рис. 1 показан продольный разрез подшипника ступенчатого типа. Конструкция содержит вал 1 и ступенчатый корпус 2 , рабочие поверхности которых образуют входной h 1 (ф , t ) = h ₀ - e ( t ) cos (ф) и выходной h ₂(ф , t ) = h 1 (ф , t ) - 5 несущие смазочные зазоры длины l 1 и l ₂ = l - l 1 соответственно, где ф - окружная координата, t - текущее время, 5 - высота ступени, l - длина подшипника, h ₀ - толщина входного зазора при соосном расположении вала и корпуса, e – эксцентриситет вала. Газовая смазка поступает в подшипник через его торец под постоянным давлением p s . Преодолев гидравлическое сопротивление входного зазора, газ дросселирует на стыке ступеней, обеспечивая на нем переменное давление p k (ф , t ) и, следовательно, несущую способность подшипника в целом, затем через выходной зазор истекает в окружающую среду под давлением Р а .

При моделировании движения подшипника полагали, что соблюдается параллельность осей корпуса и вала. Исследование характеристик подшипника проведено с использованием безразмерных величин. За масштабы приняты: радиус вала r ₀ - для линейных размеров; входное давление p a - для давлений; п r ₀ ² p a - для сил; h ₀ ³ p a ² /pRT - для массовых расходов газа; h ₀ - для зазоров и эксцентриситета вала, где и - вязкость смазки, R , T - универсальная газовая постоянная и абсолютная температура газа [2]. Далее безразмерные величины обозначены прописными буквами.

При расчете статических и динамических характеристик подшипника рассматривали малые радиальные колебания вала относительно его центрального равновесного положения.

Безразмерную функцию распределения давления во входном и выходном зазорах находили с помощью численно-аналитической методики. Методика позволяет выполнить конечно-

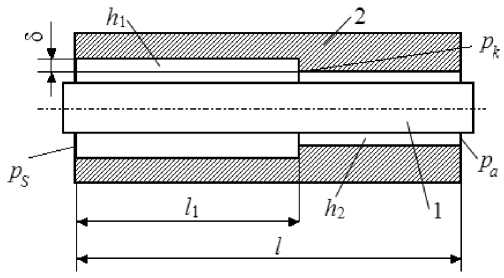
Рис. 1. Расчетная схема подшипника разностный расчет статических и динамических характеристик универсального радиального газостатического блока, математическая модель которого в безразмерном виде представляет краевую задачу для дифференциального уравнения Рейнольдса [2], описывающего течение газовой смазки в зазоре блока

| R p Ф H P H = -

P (Офт) - PM- ),P(to-) - P*-),

' p ( Z ,0 , т ) - p ( Z , 2 ..X» ( Z , 0 , , ) -» ( Z.M- ),

P (Zp0) - P„( Z)    ^

где H ( ф , т ) - H ₀ - e ( t ) Cos(ф ) - безразмерная толщина смазочного слоя блока, е - эксцентриситет вала, L = l / r . , R = r / r . - безразмерные длина блока и радиус вала; Z , т - безразмерная продольная и временная координаты; r . ,h . - масштабы линейных размеров и зазора блока;

12цг.2    „ „„ с =---2--число сдавливания газовой пленки.

ph - .

Используя методику решения линеаризованной задачи (1), находили лапласовы трансформанты несущей способности в соответствующих зазорах подшипника и предельные значения массовых расходов на стыке ступеней конструкции.

Математическая модель динамики подшипника включает также уравнение силового равновесия вала 1 с учетом его силы инерции при единичной безразмерной массе совершающего радиальные колебания вала

M = * м р . , ° -1                                     ⁽²⁾

и уравнение баланса предельных расходов на стыке ступеней

^А W 1⁽ s ) + А W 2⁽ s ) + s ^{A e (} s ) ^-A F ⁽ s ), A Q 1⁽ s )-A Q 2⁽ s ) ^- °,                    ⁽³⁾

где A ^ , kF, A W 1 , A W 2 - лапласовы трансформанты эксцентриситета вала, внешней силы и несущей способности подшипника во входном и выходном зазорах, A Q 1 A Q ₂ - лапласовы транс-форманты упомянутых расходов, m - масса вала, 1 ₀ - масштаб текущего времени, 5 - переменная интегрального преобразования Лапласа [3].

Результаты исследования

В расчетах использовали входные безразмерные параметры: n - число делений используемой конечно-разностной сетки, безразмерное входное давление P S , коэффициент настрой^ки давления ^{на стыке} ступеней х = ( P 0 -1)/( P s -1) е ^[0, 1] при ^{соосном} расположении ^вала и корпуса, длину подшипника L, коэффициент удлинения входного зазор, k = L , / L о [0, 1], ст = 12ur„ / p„h_nt„ - число сдавливания газовой пленки (этот параметр оказывает влияние лишь на динамические характеристики подшипника).

Рассчитывали безразмерную статическую податливость подшипника K = Ae (0)/ A F (0) и степень его устойчивости n = -Max Re { s k }, которая обратно пропорциональна продолжитель- – 285 –

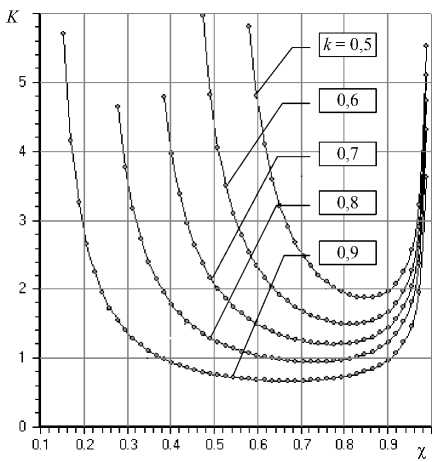
Рис. 2. Зависимость статической податливости K от коэффициента х при n = 16; Ps = 5; L = 1,5 для различных значений коэффициента k ности переходного процесса, где sk – корни характеристического уравнения модели (1) – (3), β – мнимая часть корня sk, для которого Re {sk} = –η. Критерий ηопределяет скорость затухания переходного процесса в динамической системе.

На рис. 2 показаны графики зависимости статической податливости K от коэффициента настройки χ для различных значений относительного удлинения k входного зазора.

Видно, что начиная с определенных значений к и х подшипник приобретает податливость ( K > 0). Анализ модели показывает, что это имеет место при 1– k < χ < 1. Так, если принять к = 0,8, то K > 0 при х > 0,2. Представленные на рис. 3 кривые имеют экстремальный характер, что свидетельствует о существовании оптимального с точки зрения минимума податливости значения коэффициента настройки χ. Например, для k = 0,8, как видно из графика, таким значением будет χ ≈ 0,7. Видно также, что чем больше удлинение k, тем меньше оптимальное значение податливости K . Таким образом, с точки зрения характеристик статики подшипник тем лучше, чем больше относительное удлинение k входного зазора.

Как показывают сравнение зависимостей, изображенных на рис. 4 и 5, подшипник всегда устойчив (η > 0) в областях положительной податливости K > 0. Наилучшие с точки зрения быстродействия значения параметров k и χ также находятся в области умеренных и больших значений, то есть чем меньше податливость подшипника, тем, как правило, выше его быстродействие.

Быстродействие подшипника в значительной мере зависит от числа сдавливания σ. Это видно из графиков зависимостей η(σ), которые показаны на рис. 4. Зависимости также имеют экстремальный характер, и их максимум соответствует наилучшему режиму динамики подшипника. Так, при х = 0,8 максимальное значение п ~ 1,2 имеет место при omax = 3,4. Анализ

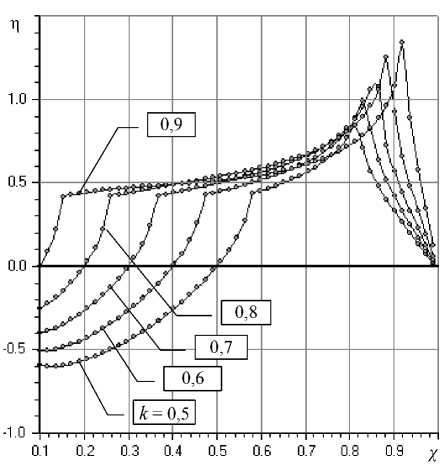
Рис. 3. Графики зависимости степени устойчивости η от коэффициента χ для n = 16; P s = 5; L = 1,5; σ = 2,8 при различных значениях коэффициента k

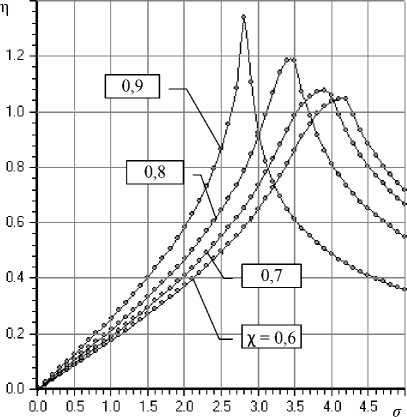
Рис. 4. Графики зависимости степени устойчивости η от числа сдавливания σ для n = 16; Ps = 5; L = 1,5; k = 0,8 при различных значениях коэффициента χ расчетных данных показал, что при σ < σmax переходные характеристики имеют колебательный характер, при σ > σmax – апериодический. Таким образом, при проектировании подшипника следует ориентироваться на значения σ, которые лежат в области апериодичности переходного процесса в близкой окрестности σmax, поскольку им соответствует больший запас устойчивости конструкции. Для приведенного примера можно принять σ = 3,5.

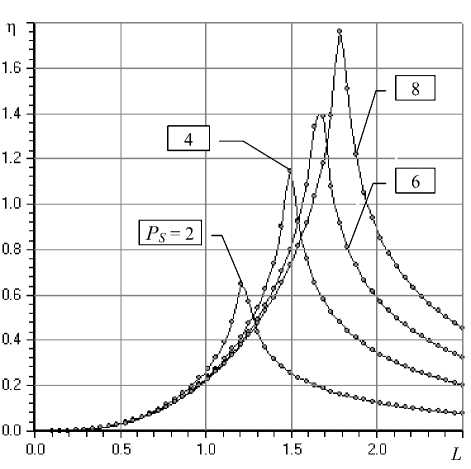
Рис. 5. Графики зависимости степени устойчивости η от относительной длины L для n = 16; χ = 0,85; k = 0,85; σ = 2,8 при различных значениях входного давления P S

Используя это значение, можно, например, найти размерный зазор h ₀ оптимального по быстродействию подшипника. Воспользовавшись (2) и исключив из выражения для σ масштаб времени t ₀, получим формулу для вычисления этого зазора:

144 πr ₀ µ ² h ₀= r ₀ 5       ₂

.

mσ pa

Уравнение баланса статических расходов на стыке ступеней после несложных преобразований позволяет указать формулу для вычисления высоты ступени подшипника:

• 5 = h 0 ( 1 - 3/ ( 1/х-1 )( 1/ к -1 ) ) .

Экстремальный характер имеют и зависимости n( L ), графики которых для различных значений входного давления P_S изображены на рис. 5. Наилучшие показатели динамики имеют конструкции относительной длины L = 1 - 2. Увеличение входного давления является фактором повышения быстродействия подшипника, при этом пик быстродействия смещается в сторону б о льших L .

Результаты проведенного исследования позволяют сделать заключение о том, что при проектировании радиальных газостатических подшипников ступенчатого типа следует учитывать не только статические характеристики, но также критерии оценки динамики переходных процессов. Как правило, зависимости последних носят экстремальный характер, что дает возможность рассчитать оптимальные значения ряда параметров подшипника, таких, например, как длина и толщина его зазоров.