Характеристики системы дифференциальных уравнений плоского напряженного состояния, соответствующие инвариантным решениям

Полученыуравнения характеристик системы дифференциальных уравнений плоского напряженного состояния, соответствующие инвариантным решениям. Построены графики этихуравнений.

Рассмотрим систему уравнений плоского напряженного состояния при условии постоянства интенсивности касательных напряжений. Данная система дифференциальных уравнений вместе с условием пластичности может быть приведена к виду [1]

dr

^r   tg(arctg( A²e ^^ю ) + 2 - 2arccos(ct^g “ ))

d 6 .

Используя равенство 6 = C - Х ( ® ) - arctg( Ae

^^^. .

-А®), с

У3   „   1     ^д®, У3 . _ д®  Эф .

—cos2 ф ctg®-- 1-- sin2ф--- = 0,

2          2       I d x 2 d y  d y

учетом

У3 . _ d® ^fУ3   _    1      ^d®  дф _

— sin2 ф —cos2 ф + —ctg ® 1 = 0,

2 d x 2          2       Id y   d x

имеем

где ® = ® ( x , y ), ф = ф ( x , y ) - неизвестные функции.

Автором совместно с О. Н. Ждановым найдено инва

риантное решение системы (1):

r

B2 e " ^®+ B2 A2 eV3® sin®

ф = 6 + arctg( A ² e ^® ), (2)

где A , B - произвольные постоянные; r , 6 - полярные

координаты.

Получим характеристики, соответствующие инвариантному решению (2).

Как известно [1], уравнения характеристик системы (1) имеют вид

dy = tg ( ф ± v ) dx ,                 (3)

и соотношения на характеристики выглядят следующим образом:

Х(®)±ф= C,      i (4)

п 1      zctg®           1 “ V3- 4cos2® где V = - — - arccos( ), %(®) = - - ----:

2 2 V3            2 П sin ®

п

С - произвольная постоянная [1]; 6 < ® < —. Рассмотрим характеристику dy = tg(ф + V) dx(5)

и соответствующее соотношение на характеристики х ( ® ) + ф = C .

Перейдя к полярным координатам, запишем уравнение (5) в виде sin6 dr + rcos6 d 6 = tg(6 + arctg( A2 e~ ^®) +

. : 1        .ctg ®

+ 2 - 2 arccos(     )) ' (cos 6 dr - r sin 6 d 6 ).

Дифференциальное уравнение (5) приведем к урав

нению с разделяющимися переменными:

dr r

1 + tg(6 + arctg( A ² e ^® ) + — -—arccos(ctg®)) ■ tg6

=------------- _ . : ²1² -----cig®³------ d ⁶

tg(6 + arctg( A ² e   ) + 2 - 2arccos( JL )) - tg6

После упрощений получим

формулы

1 У3 - 4cos ²® , d 6 =-- d ®+

2    sin ®

A 2 43e - ^V3®

1 + A⁴ e ² ®

d ® ,

f dr = f-------------- 1                    d 6 .

^r    tg(arctg( A ² e ^® ) + 2 - 2arccos(2gp))

Упростив это выражение, получим

J dr = j - tg(arctg( A ² e "^V3® )

1      ^tg ® f 1

- —arccos(—^)) —

2 У3 2

1 У 3 - 4cos ² ®

Таким образом, r =

- arctg( A ² e ^®

-

A ²V3 e - ^V3® '

sin ®        1 ₊ A⁴ e ^{2 v 3}®

1       zctg® '

exp( f tg (2arccos(—"2^ -

))) ^f 1 У3 - 4cos ² ® ₊ A ²У3 e- ^3® ) 2    sin ®       1 + A⁴ e -²^3®

d ®.

d ® ) + C .

Для того чтобы определить значение константы С _р а

п

5 п

также учитывая что — < ® < — , запишем решение г : 66

, Г. /1        /ctg® r = exp(l tg(—arccos(—-

П:     2 V3

- arctg( A¹ e ~ ^®

))) f 1 У 3 - 4cos ² ® ₊ _ A 2/3 e Zfl ' 2    sin ®      1 + A⁴ e ~²^®

d ® ).

/

Тогда уравнения первого семейства характеристик, соответствующих инвариантному решению (2), имеют вид

6 ( ® ) = C + 1 f ^{73 -} 4^cos 2 ® d ®- arctg( A ² e -^® ),

2 П     sin ®

, ®z 1       zctg®                  f 1 si 3 - 4cos2® A 2Ф3e ~V5® r = exp( I tg(- arccos(^=- - arctg(A e ))) I  ----:------+----—-e-

П 2          3                    I 2 sin ®       1 + A⁴e"^г*®

Аналогичным образом получаем уравнения характеристик второго семейства:

6 ( ® ) = C - ¹ f ^³ 4 ^cos — d ®- arctg( A²e ^v5”),

2 :     sin ®

.“f. . 1       .ctg ®                    ^f 1 4 3 - 4cos² ®    A ² Vs e ~^"

r = exp( tg(--arccos(      - arctg( A e ^J )))!-------_;------- +

:      2 V3                     I 2    sin ®       1 + A⁴ e-2^Г3 “

Автором с использованием математического пакета MathCAD были построены графики уравнений характеристик, соответствующих решению (2), при различных

Математика, механика, информатика значениях параметра^. В качестве примера представим график, получающийся при Л = 1 (рис. 1).

стикам первого семейства, полученным в данной работе (при Л = 1, С = 0).

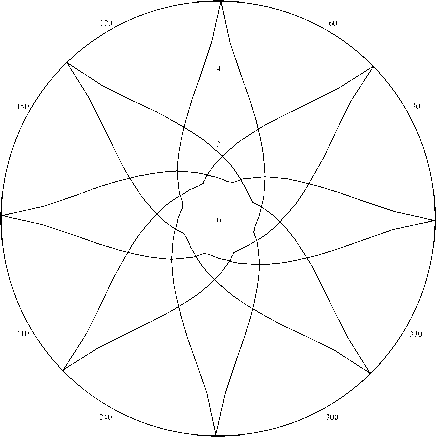
Рис. 1

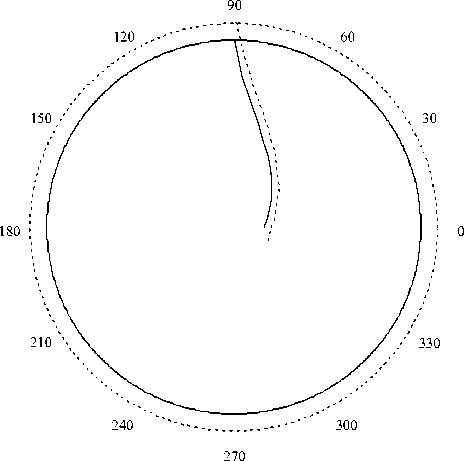
Рис. 2

Для сравнения приведем ветку, соответствующую характеристикам первого семейства, найденным В. В. Соколовским [1] (рис. 2). Напомним, что уравнения характеристик В. В. Соколовского имеют вид

1 3 ^- 4cos ® ⁶⁽® ) = C +

2 я d ®,

sin ®

r¹ = A ^Oexp²^³²^ ® ))- sin ®             3

где С ₁ , Л j - произвольные константы. Ниже представлена ветка характеристик, получающихся при A 1 = 1, C 1 = П Пунктиром выделена ветка, соответствующая характери-

Таким образом, получены характеристики системы уравнений плоского напряженного состояния, соответствующие новым инвариантным решениям этой системы, найдены автором совместно с О. Н. Ждановым. Наблюдается различие между характеристиками этой системы, представленными в данной статье (при значении параметра) и характеристиками, полученными ранее В. В. Соколовским [1].

Автор благодарит О. Н. Жданова и С. И. Сенашова за помощь в постановке задачи.