Характеристики виртуальной диаграммы ритма сердца

Предложено понятие и процедура формирования виртуальной диаграммы ритма сердца (ДРС). Исследованы ее характеристики. Приведены результаты сравнительного параметрического и структурнотопологического анализа реальных ДРС группы здоровых обследуемых и соответствующих им (по величине σ) виртуальных ДРС. Определено, что виртуальная ДРС представляет хаотическую составляющую ритма и является динамической базой механизмов адаптации организма к внешним влияниям.

Постановка задачи

Ритмическая активность сердца является интегральным показателем функционального состояния организма (ФСО) [1~2], поскольку сердечный ритм регулируется нервными и гуморальными факторами с участием вегетативной нервной системы,а также более высокими отделами центральной нервной системы [2].Наличие и повторяемость структурных особенностей на диаграммах работы сердца при патогенезе позволило создать определенную базу симптоматики заболеваний.Однако,причины и механизмы возникновения таких особенностей не ясны [2].Это делает проблематичным донозологическое прогнозирование их зарождения,появления и разви-тия.Причиной этого является сильное ограничение в применении физического анализа ритмических процессов сердца из-за отсутствия адекватного универсального эталона ритма сердца в норме.Поэтому и понятию нормы ФСО посредством ритмических характеристик сердца нет адекватного определения.

Параметрическая оценка нормы ФСО обычно проводится при помощи метода оценки вариабельности сердечного ритма (ВСР)[3].Параметры ВСР являются взаимозависимыми.Они сильно зависят как от длины записи ЭКГ,так и от психоэмоционального состояния и даже от положения тела испытуемо-гов состоянии покоя.Ясно,что такая оценка является очень условной.До настоящего времени применение метода физических аналогий и сопоставлений для реальных диаграмм ритма сердца (ДРС)не было ус-пешным.Отсутствие эталонной ДРС приводило к необходимости попарному сравнению ДРС или величин параметров ВРС.Целью данной работы является поиск эталонного ритма сердца при ФСО в норме.

Виртуальная диаграмма ритма сердца

Виртуальной (воображаемой)диаграммой ритма сердца (вДРС)автор называет диаграмму,построен-нуюгенерациейслучайныхчиселпонормальномуза-кону распределения около среднего значения RR-интервала (< X >)с назначенной величиной стандартного отклонения (σ)[4].ВДРС,созданная по величине σ реальной ДРС,является виртуальной,воспринимае-мой как реальная (рис. 1 а, б ).

Приведем результаты сравнительного анализа параметров реальных ДРС группы молодых условно здоровых обследуемых (УЗО) и соответствующих им (по величине σ) вДРС. В состав группы 32 УЗО входили 20 юношей и 12 девушек в возрасте от 18 до 21 года. Двадцатиминутные регистрации электрокардиограмм (ЭКГ) были проведены по стандартной методике [3-4] за период февраль-март 2008 г. в режиме покоя, сидя. Все ЭКГ конвертировались в последовательности RR-интервалов с получением ДРС.

Известно [3, 4], что величина стандартного отклонения σ имеет тенденцию к медленному росту с ростом объема n выборочной реализации ДРС. Поэтому возникает необходимость определения динамики величины σ с ростом размера цифрового ряда вДРС. Для этой цели в Excel 7.0 было создано около сотни вДРС для разных величин σ (от 1 до 300 мС) при заданном <  X > = 937 мС (64 уд/мин) и с объемом выборки n от 50 до 10000 отсчетов. На рис. 2 показана динамика σ от размера выборки в форме графика функции σ( n ), построенного для вДРС, сгенерированной для σ = 70 мС. Для используемой программы генерации σ = 70,0 ± 2,6 мС (при уровне значимости α = 0,05). Максимальные отклонения от принятого значения характерны для n < 500. Исключая из рассмотрения малые объемы выборки с n = (50 … 300), получаем σ = 69,9 ± 1,1 мС. В первом случае относительная погрешность ε_σ составляет 7,4 %, во втором – 3,1 %. Таким образом, назначенная при генерации вДРС с n ≥ 500 величина σ = 70 мС сохраняется внутри интервала значений (68,8 ÷ 71) мС с вероятностью не менее 0,95.

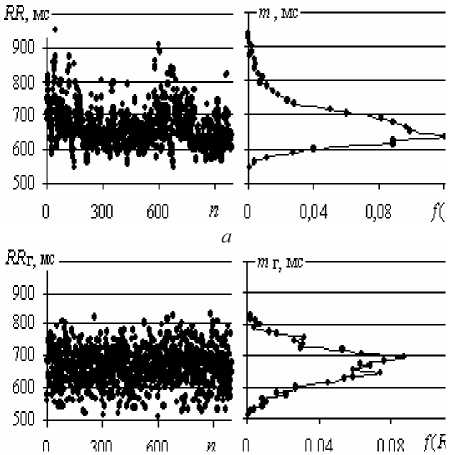
Рис. 1. Точечные графики ДРС ( а ) и вДРС ( б ) и соответствующих горизонтальных полигонов распределений УЗО Е-вой (21 год)

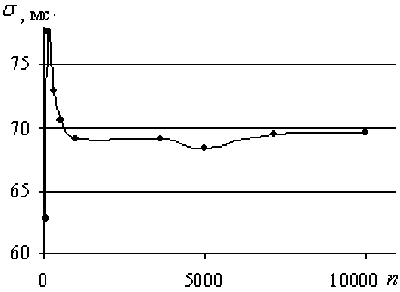
Рис. 2. График зависимости σ( n ) для вДРС

Очевидно, что изменение величины σ при генерации вДРС приводит к перераспределению значений RR-интервалов на ярусной вДРС [4-6]. При этом меняются основные параметры ВСР и структурно-топологические параметры диаграммы: вариационный размах Δ X , количество «рабо-

чих» ярусов k _я* [4-5], количество информации I Σ и информационная энтропия I * [4; 7] ДРС.

Для используемой программы генерации случайных чисел по нормальному закону распределения Δ X слабо зависит от размера цифрового ряда в интервале 500 <  n < 5000 и сильно зависит для n > 5000 (рис. 3). Для любых значений n функция Δ X (σ) имеет вид Δ X = а σ, где линейный коэффициент а принимает значения 13,53, 6,76, 6,39 и 5,97 для значений n , равных 10000, 3600, 1000 и 500, соответственно и при коэффициенте достоверности линейной аппроксимации R ² = 1. В интервале значений 500 <  n < 5000 и для σ = 69,9 ± 1,1 мс величина Δ X = 453 мС с относительной погрешностью ε _ΔX = 11,5 %. В пределах 1000 <  n < 2000, характерных для двадцатиминутной регистрации ЭКГ, ε _ΔX < 5%. Величина σ для вДРС с ростом n не меняется (см. рис. 1), поэтому можно принять неизменным и вариационный размах.

Для ДРС группы УЗО в интервале значений 1223 <  n < 2437 и для σ = 72,9 ± 8,9 мС величина Δ X = 439 мС с относительной погрешностью ε_{Δ X} = 18,7 %. Функция Δ X (σ) имеет вид Δ X = а σ, где линейный коэффициент а = 5,82при коэффициенте достоверности линейной аппроксимации R ² = 0,68.

Все основные параметры ( X ) вариабельности сердечного ритма (ВСР) временной области [2], определенные по вДРС и в сравнении с ДРС здоровых людей, имеют качественно одинаковую функциональную зависимость от σ и практически не зависят от объема n выборки (рис. 3).

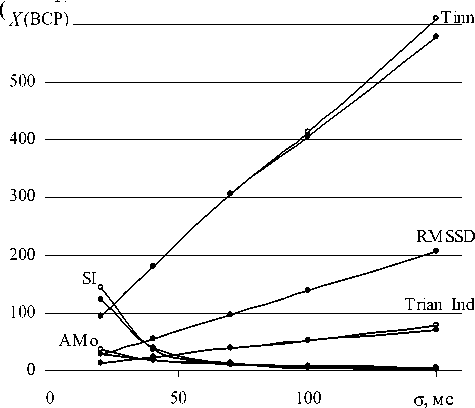
Рис. 3. Графические зависимости параметров ВСР от σ при n = 1000 (•) и n = 3600 (о)

В частотной области анализа полная спектральная мощность (TP),определенная для вДРС,сильно зависит от о и более слабо от п (рис. 4а).Эти зависимос- ти для вДРС и ДРС качественно совпадают,однако распределение составляющих мощностей по четырем частотным диапазонам (рис. 46) прямо противо-положно.Это связано с тем,что при фиксированных границах частотных диапазонов спектр плотности мощности вДРС широкополосный,а спектр плотности мощности ДРС здорового молодого человека в состоянии абсолютного покоя – узкополосный с максимумом на околонулевых частотах [3-4].

При простом сравнении функциональных зависимостей параметров ВСР для виртуальной и реальной ДРС выяснились основные сходства и различия в механизмах структуризации при их формировании.Обе ДРС формируются с одним шагом дискретизации (Δ x = 1 мС),поэтому на диаграммах значения RR-интервалов располагаются ярусно [4-6].Такая ярусная структура диаграмм формируется посредством микро-переходов между отдельными ярусами.При формировании ярусных структур при переходе от отсчета к отсчету для вДРС превалируют случайные (хаоти-ческие)по направлению и величине переходы между ярусами,а для ДРС – и случайные,и регулируемые.

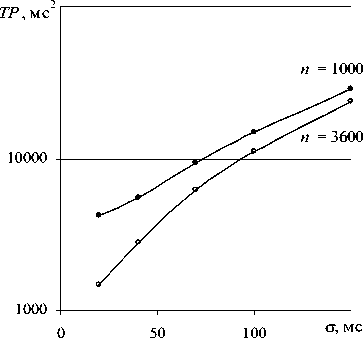
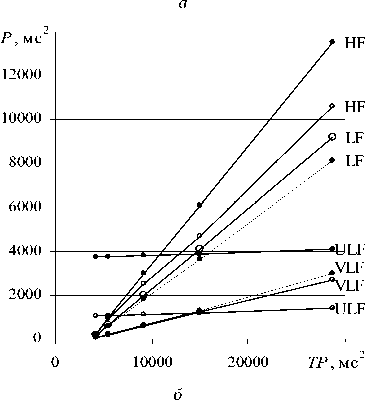
Рис. 4. Графические зависимости полной спектральной мощности (ТР) вДРС от о (а) и составляющих спектральных мощностей (P) по четырем частотным диапазонам от TPпри n = 1000 (•) и n = 3600 (о) (б)

При формировании вДРС все микропереходы равновероятны. Ярусная структура с заданными первичными значениями σ и Δ x наполняется однородно с учетом нормального закона распределения. При формировании ДРС предпочтение отдается соседним переходам. Это легко проверяется при построении дифференциальной ДРС. Значения σ (и Δ X ) являются вторичными и обеспечиваются внешними низкочастотными процессами, проявляющихся в формах медленных волн первого и второго порядков [1]. Поэтому при формировании вДРС превалируют «процессы» диапазонов высоких (HF) и низких (LF) частот, а в случае ДРС превалируют процессы диапазонов очень низких (VLF) и ультранизких (ULF) частот [3].

Таким образом, вДРС является математической моделью ДРС с первично заданной величиной σ и распределением по нормальному закону. Ярусная структура вДРС, определенная постоянной и неравной нулю величиной Δ x , формируется без внешней регуляции, но под заданные ограничения. Наполнение спектральных диапазонов VLF и ULF является ложным, связанным с недостатками Фурье-преобразования [8].

В формировании реальной ДРС на базе собственной функции автоматии сердца участвуют два внешних механизма: детерминистский внешней регуляции ритма с частотным механизмом наполнения ярусами и самих ярусов и хаотический, связанный с шумом внешних и внутренних влияний. Проявление первого механизма приводит к структуризации ярусной диаграммы, проявление второго – к деструктуризации. В рамках такого разделения системного процесса формирования ритма вДРС представляет только хаотическую составляющую с максимальной степенью неупорядоченности значений в рамках заданной величины σ и является динамической базой механизмов адаптации организма к внешним влияниям.

Здесь необходимо отметить, что вДРС формируется под величину σ, равную расчетной для исходной реальной ДРС. Очевидно, что «истинная» хаотическая составляющая, «выделенная» (если это возможно) из реальной ДРС, вообще говоря, будет иметь другую величину σ.

Для определения количества рабочих ярусов k _я* на диаграммах ритма был создан программный модуль «идентификации ярусов» [4]. На рис. 5 а приведены расчетные данные числа рабочих ярусов для вДРС, созданных для разных σ и n , а на рис. 5 б представлены те же данные по отношению к общему числу ярусов, захватываемых вариационным размахом.

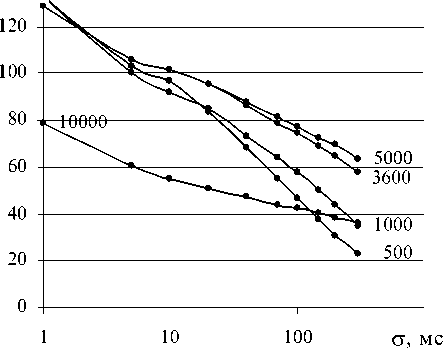
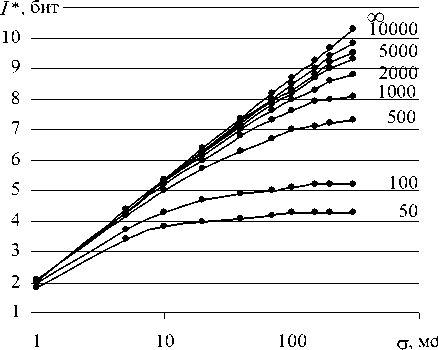
Распределение значений RR-интервалов на ярусах диаграммы может быть представлено в форме количества возможных комбинаций Г для реализации этого распределения или количества информации I ^ , недостающего для описания для его описания [4; 7] (рис. 6 а ). Тогда среднее количество информации, приходящееся на один отсчет, определяет информационную энтропию диаграммы ритма I *= I ^ /n. Функция I *( о , n )имеет границу определения и при n → ∞ она совпадает с функцией H ( X ) математического ожидания энтропии системы X , состояния которой распределены по нормальному закону (рис. 6б) [9-10]. При росте n величина I * всегда растет и при n → ∞ принимает максимально возможное значение при заданном σ [4].

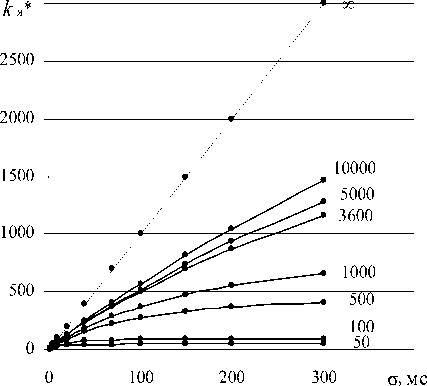
а к, %

б

Рис. 5. Графики зависимостей числа рабочих ярусов на вДРС от σ и n

Сравнивая графики на рис. 5а и 6б, можно увидеть, что ход исследуемых функций одинако- вый для соответствующих значений n. Также очевидно, что существует функция kя соответствующая граничной прямой на рис. 6б.

«Рождение» каждого нового яруса при росте n фиксируется разными параметрами поразному. Число «рабочих» ярусов прирастает на 1, если ярус «открылся» одним значением. Величины I ^ и I* на это не реагируют и чувствуют лишь подтверждение этого открытия еще одним значением. Поэтому ход функции I *( n ) всегда запаздывает относительно k _я*( n ). Отсюда следует очевидное правило формирования диаграммы ритма: рост k _я* первичен по отношению к функции их неупорядоченного формирования.

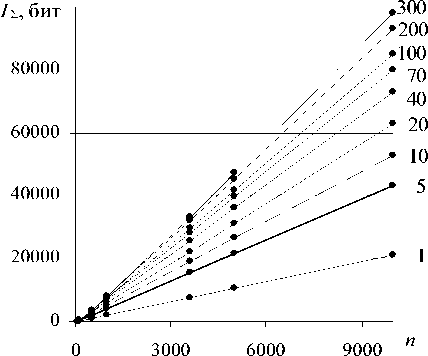
а

б

Рис. 6. Графики зависимости количества информации

I^,g, n ) ( а ) и информационной энтропии I* (о, n ) ( б) для вДРС

На рис. 7 приведен график зависимости I*(kя*) в полулогарифмическом масштабе для разных n, построенный по возрастающему ряду значений (1; 5; 10 …. 300). Видно, что при росте числа ярусов зависимость степени неупорядоченности ярусной структуры вДРС от числа ярусов на ней слабеет по логарифмическому закону.

Спектр оконной функции I *( n _o) вДРС всегда широкополосный, а график этой функции является горизонтальной линией с малыми флуктуациями, определенными погрешностью вычисления (см. рис. 6 б ). Спектр оконной функции I *( n _o) для ДРС здоровых молодых людей также широкополосный, а график этой функции также является горизонтальной линией с небольшими флуктуациями, определенными как погрешностью вычисления, так и отклонениями текущего состояниям [11].

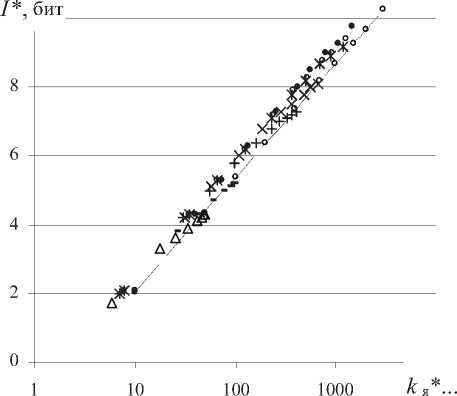
Рис. 7. График зависимости I *( k _я*) для возрастающего ряда значений σ и для разных n : 50 (Δ), 100 (-), 500 (+), 1000 (х), 3600 (ж), 10000 (•) и n → ∞ (о) с уравнением трендовой линии I * = log₂(k_я*) – 1,28 при R ² = 1

Предложенные характеристики вДРС могут быть полезны при сравнении значений параметров реальной ДРС, описывающей регулируемое формирование диаграммы и вДРС, описывающей не регулируемое хаотическое формирование диаграм-мы.Применение структурно-топологических характеристик (к я *, I ^ , I *) при анализе диаграмм ритма имеет очевидные преимущества над использованием параметров ВСР,так как последние могут быть адекватными в применении лишь для стационарных процессов.

Выводы

Виртуальная ДРС является математической мо-дельюДРСспервичнозаданнойвеличинойстандар-тного отклонения (σ) и распределением по нормальному закону. Ярусная структура вДРС формируется без внешней регуляции и представляет хаотическую составляющую ритма с максимальной степенью неупорядоченности в рамках заданной величины σ .

Основные параметры вариабельности сердечного ритма временной области,определенные по вДРС и в сравнении с ДРС здоровых людей,имеют качественно одинаковую функциональную зависимость от о и практически не зависят от объема n выборки.Для вДРС с ростом объема выборки назначенная величи-настандартногоотклоненияпрактическинеменяется, величинавариационного размахаоченьмедленно растет в пределах интервала 500 <  n < 5000,число ярусов и информационная энтропия растут к насыщению,а количество информации I Σ растет линейно.

Виртуальная диаграмма ритма сердца, представляющая хаотическую составляющую ритма,является динамическойбазоймеханизмовадаптацииорганизма к внешним влияниям.Снижение уровня хаотической составляющей для ДРС определяется уменьшением величин k _я* и I *,что означает включение механизмов резонансного отклика ритма сердца и захват им ритмов внешней среды.Возникающая дисгармония в отношениях ритмов приводит к аритмии сердца.