Характерные углы контактного взаимодействия в двухвалковом модуле

DOI:

Технологические процессы в валковых машинах осуществляются в их основном рабочем органе – в двухвалковом модуле, в результате контактного взаимодействия обрабатываемого материала с парами валков по кривым контакта валков. В кривом контакте каждого валка находятся такие точки, по которым происходят какие-либо явления напряженнодеформационного состояния, например, максимальное нормальное напряжение, максимальная деформация (обрабатываемого материала и покрытия валка). Такие точки называются характерными точками кривого контакта валка [1]. Они имеют большое значение в решении контактных задач, следовательно, важны для параметров двухвалкового модуля.

Схема контактного взаимодействия в симметричном двухвалковом модуле представлена на рис.1, где 1, 2 – валки с радиусами R, 3, 4 - эластичные покрытия валков с толщинами Л, 5 - обрабатываемый материал с толщинами - начальной 61 и конечной 62.

В кривом контакте валка выделены семь характерных точек в установившемся режиме: А 1 — начальная точка; А 2 — конечная точка; Л₃ — точка максимальной деформации; А₄ — точка, разделяющая зоны скольжения отставания от зоны прилипания; Л₅ — точка, разделяющая зоны прилипания от зоны скольжения опережения; Л₆ — нейтральная точка; Л₇ — точка максимума нормального напряжения.

Пусть характерные точки А_[: (i = 1,7) определяются соответствующими характерными углами a i :

a i — угол захвата; a₂ — угол выхода; a₃ — угол максимальной деформации;а₄ — угол, разделяющий зоны скольжения отставания от зоны прилипания; a₅ — угол, разделяющий зоны прилипания от зоны скольжения опережения; a₆ — нейтральный угол; a₇ — угол, определяющий максимум нормального напряжения.

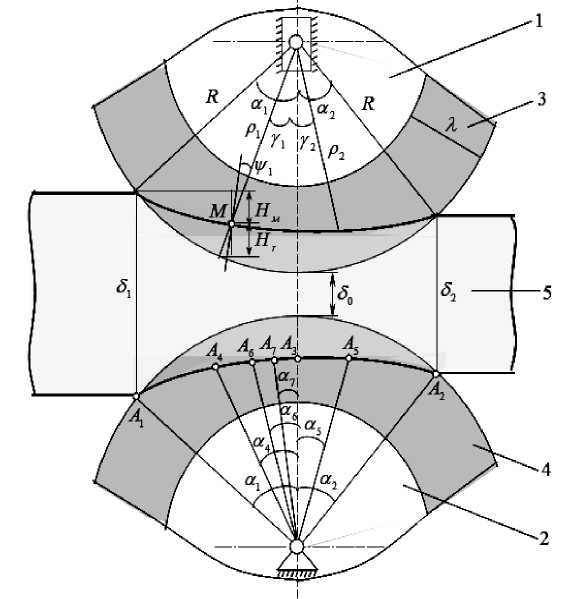
Рисунок 1. Схема контактного взаимодействия в установившемся режиме.

Figure 1. Scheme of contact interaction in steady state.

В одних исследованиях [2-8], посвященных к решению контактных задач двухвалковых модулей, найдены некоторые из перечисленных углов. Многие из них сосредоточены на определении углов захвата и нейтрального угла в прокатке металлов. В других исследованиях некоторые из характерных точек определены опытным путем [6-8].

Целью работы является определение расчетных формул характерных углов кривых контакта валков в установившемся режиме на основе анализа геометрических, кинематических и силовых условий напряженно-деформационного состояния в зоне контакта валков двухвалкового модуля.

МАТЕРИАЛЫ И МЕТОДЫ

Геометрические     условия     определяют характерные углы кривого контакта а, а2 и а3, кинематические - а4 и а5, силовые - а6 и а7.

Углы а4,а5,а6 и а7 определяем на основе анализа кинематических и силовых условий с применением      ранее      разработанных математических моделей формы кривых контакта валка, напряжений трения и закономерностей распределения контактных нормальных и касательных напряжений [1, 4].

Углы а 1 и а₂ в установившемся режиме зависят от угла начального захвата.

Рассматриваем начальный захват слоя материала в двухвалковом модуле (рис. 2).

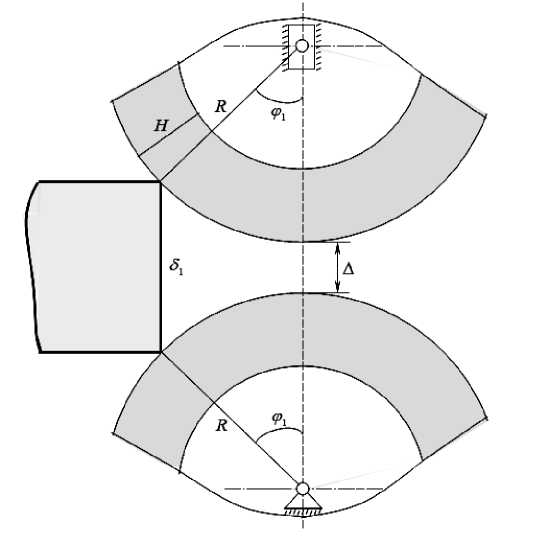
Рисунок 2. Схема начального контакта слоя материала и покрытия валков.

Figure 2. Initial contact diagram of the material layer and the roll coating.

Из рисунка 2 следует:

2R соsф + 61 = 2R+1, где ф — угол захвата в начальном контакте, R — радиус валка, 61 — начальная толщина слоя материала, 21 — расстояние (зазор) между валками в начальном контакте.

или в первом приближении:

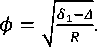
Угол захвата в началньном контакте

оценивается условиями захвата.

Отсюда следует:

■ 2 ^ф

^Sln2 2" =

— 1

Угол захвата для симметричного двухвалкового модуля с двумя приводними валками оценивается условием [7]:

4R

ф

Отсюда находим предельное значение угла захвата

Ф = V.              (2)

РЕЗУЛЬТАТЫ

Для    рассматриваемого    симметричного двухвалкового модуля форма кривой контакта валка определяется системой уравнений [10]:

fТЙТ⁽¹+ ^к1 ^71) ’^ ^{— а}1 - ^1 - ⁰’

1 + ^1           CUd fl

^Р    ) R            cos а                             ( )

^У1^^’^

В начале процесса взаимодействия слой материала и покрытия валка входят в контакт, они сжимаются, а затем восстанавливают деформацию. Вследствие этого, расстояние между валками меняется, и в установившемся режиме имеет значение 8₀.

Аналогично формуле (1), находим угол захвата в установившемся режиме:

а1

-1

S1-S_OR

6₀ -расстояние  (зазор) между валками в

установившемся режиме.

Отсюда следует:

а1 = ф

181 - 8о Р1—^Л

или с учетом равенства (2):

а1

, I^Si—^So у 81—л

Угол выхода определяем аналогично

а2

182—50 ^—^Л'

где 82 — конечная толщина слоя материала.

где    к1 — отношение    скорости сжатия деформаций покрытия к соответствующей скорости материала, к2 — отношение скорости восстановления деформаций покрытия к соответствующей скорости материала.

Углы а4 и а5 определяем на основе анализа модулей напряжений трения в зоне контакта валка.

Модель напряжений трения слоя материала в зоне скольжения отставания выражается как [11]:

^1т = ^—fn1m ;^^Т^~Г ’  ^—а1 ^-/1 ^{- —а}4’   ⁽⁷⁾

|’sll-a1)l где f —коэффициент трения слоя материала о поверхности контакта покрытия валка, ^1т,^ vsi(Y1)’^ п1т — значения касательного напряжения, скорости скольжения и нормального напряжения в точке, определяемой углом Y1,vsl(—а1) — скорости скольжения в точке, определяемой углом (—а1).

Согласно [3], скорость скольжения v_Ck(y1), определяется как:

Vsi(Ю = wjp2 +р ‘ 2 — Vm COS(Y1 — Ф1),   (8)

где tg^1 = ^1,               (9)

Pl

Углы максимальной деформации определяются обычно на основе экспериментального исследования. Экспериментальные исследования показали, что в двухвалковых модулях, где валки имеют эластичное покрытие, это смещение незначительно [1, 10], например, при валковом прессовании кожи это смещение кривой контакта составляет всего 0,09-1,75% [1]. Поэтому полагают, что характерная точка максимальной деформации контактирующих тел лежит на линии центров, следовательно:

здесь ы —угловая скорость валка.

Из равенства (8), имеем vsl(—а1) = mR — vmcos а1,      (10)

где v_m —скорость обрабатываемого материала.

Из первого уравнения системы (6) следует

Rkicosai sin^i

1+ki cos²fi

Определяем р₁(—а₄) и р1(—а₄), принимая при

аз = 0.                  (5)

этом sin а₄ ~ а₄,п cos а₄ ~ 1:

Для определения остальных характерных углов требуется математическая модель кривого контакта валка.

Р1(^—а4) =^(^{1 + COSа}1⁾’ Р1 ^(—а4⁾=

—

Rk_±cos а ---;— а4.

1+ki

Подставив значения р1(-«4) и р'1 (-«4) в равенства (8), получаем

Vsi^(-«4)

coR(1+ki cos ai)-Vm(1+ki) 1+ki

Из равенства (11), имеем t1m(-«4) _   ,. ^si(-«4)

ⁿ1m^(-«4)      Vsi^(-ai)

где     P = tg—,     F,Q — внешние силы, действующие на валок.

Отсюда получаем

t^r(«4)

——— = ^tg^(-«4 ^-Ф1^(-«4) + P) ^1r (—«4)

или, учитывая выражения (13) и считая sin «4 ~ или с учетом равенств (14) и (16)

«4,^ cos «4 ~ 1,

^imC-Oil ”1m(-“4)

_f aR(1+k_i cos a_i)-v_m(1+k_i) (1+ki)(^R-Vm cos ai)  ^.  '   '

tir(-a4) _   Qa4-F(1+kiC0S ai)

-----—--

.

ⁿir(-a4)        Q(1+ki cos ai)

Согласно [11], модель напряжений трения для приводного валка, имеет вид

tir = nirtg(Yi --Ф1+ p),  -Ф1

Согласно закону Ньютона в каждой точке зоны контакта выполняются условия: t_1m(Y) = t_1r(Y), ⁿ1m⁽Y) = ⁿ1r⁽Y).

С учетом этих условий, из равенств (13) и (15), находим угол «4, разделяющий зоны скольжения отставания от зоны прилипания

«4 =

(1+ki cos ai)(fQ(uR(1+ki cos ai)-vm(1+ki)')+F(1+ki)(uR-vm cos ai)) Q(1+ki)(uR-vm cos ai)

Из рисунка 1 видно, что cos «1

2R-(Si-S₀)

.

2R

С учетом выражения (17) из равенства (16), имеем

«4

(2(1+ki)R-ki(Si-S₀))(aR(2(1+ki)R(fQ+—)-ki(Si-S₀)fQ)   (2(1+ki)R-ki(Si-S₀))(Vm(1+ki)(2R(fQ+—) + (Si-S₀)—))

--------------------------------------------------"---"---------------------------------------------------.

2(1+ki)RQ(2^R²-Vm(2R-(8i-8₀))                       2(1+ki)RQ(2^R²-Vm(2R-(8i-8₀))

Угол «5, разделяющий зоны прилипания от зоны скольжения опережения, определяем аналогично:

(2(1+k2)R-k2(62-6₀))(vR(2(1+k2)R(fQ+F)-k^^^            (2(1+k2)R-k2(82-8₀))(Vm(1+k2)(2R(fQ+F)+(82-8₀)F))

. 2(1+k2)RQ(2^R2-Vm(2R-(82-8o))                       2(1+k2)RQ(2^R2-Vm(2R-(82-8o))

Оставшиеся два характерных угла «₆ и «7 определяем на основе силовых условий.

В нейтральной точке А6, соответственно и в нейтральном угле    (-«6),    касательная напряжения равняется нулю.

Тогда из формулы (14) следует, что tg(-«6 - Ф(-«б) + p) = 0.

Отсюда с учетом выражения (9) и считая sin«₄ « «₄,^ cos«₄ « 1, находим

F(1 + k1 cos «1)«6 =------Q------ или с учетом выражения (17):

«6

F(2(1+ki)R-ki(S2-S₀))

2RQ           '

В последней характеристической точке А₇, и соответственно в угле (-«₇), нормальное напряжение достигает своего максимального значения.

Для определения угла «₇, требуется выражение нормального напряжения n1(Y1). Величина n_1m в первую очередь определяется физикомеханическими свойствами обрабатываемого материала.

В исследованиях [1, 5], посвященных изучению физико-механические свойства материалов, обрабатываемых в валковых машинах, для аналитической зависимости «напряжение – относительная деформация» используется либо эмпирическая степенная зависимость ст = Лей, либо реологическая модель Кельвина-Фойгта.

Пусть деформационная свойства обрабатываемого материала при сжатии описывается реологической моделью Кельвина-Фойгта:

d£1 ь

ТМ = Е1Е1 м + Ц1 —, где О1 м,£1 м,Е1 м,цмт - напряжения, деформация, модули упругости и вязкости обрабатываемого материала при сжатии.

Отсюда следует с1т  Е1те1т + Е1т^е1т,\^ е1т      , dY1 ’

—а1! < 0.               (21)

^п1 =    2-^ ^(Е1т^Н1 ⁺Е1т^^Н1) ^cos(Y1

(1 + ^к1)в1

^—^1).

Отсюда получаем

П1 = 7ЕЕЕ( ((Е1тН1 + /Л1тЫН1) cos(Yi — ^1) — ^(1+k1)

(Е1тН1 + Ц1т^Н1 )sin(Yi — ^1)(1 — Ф1)).

По условию максимума функции, п1 (—а₇) = 0.

Поскольку точка А7 близко к линии центров, угол а7 близок к нулю. Поэтому считаем, что sina7 ® а7,-. cos а7 ® 1.

Тогда из равенства (6), (9), (11) и (25), имеем

Фг(—а₇) = — ^ki^cosai а₇, фi(—а₇) =

¹    "      1+k₁cosa₁^{7    1}     "

kicos ai

1+ki cos al

Для любого времени t в зоне сжатия имеют место соотношения

Н1 _в + Him = Н            (22)

Н₁(—а₇) = R(1 — cos а1),  Н‘(—а₇') = Ra₇

Н1(—а7~) = —R.

или с учетом равенства Н1 _в= к1Н1 _м

1 „ Н1 м = 1+^1, где Н1 в, Н1 м — деформации покрытия валка и обрабатываемого материала в зоне сжатия.

Тогда, имеем

_   2Н1     ‘  _2Н

^£1т= (1+k₁)S₁, ^£1т= (1+k₁)S₁^.

С учетом равенств (23) из равенства (21) следует

С1т = —— (Е1тН1 + Ц1тШН1).(24)

(1+K1)S1

С учетом этих выражений из равенства (26) получаем

Н1 = R(cosy1 — cos а1), H‘ = —RsiпY1,Н =

—RCOSY1.(25)

Для рассматриваемого двухвалкового модуля, имеем

П1 = O1mC0S(Y1 — ф1)

или с учетом равенства (24)

С учетом этих выражений, получаем

(1 + к1 cos а1)²(Е_1mRa₇ — ^_1mшR) +

(Е1mR(1 — cosa1) + ^1mшRa7)a7 = 0.

Отсюда находим

^_1тш(1 + к1 cos а1)²

^а7   Е1((1 + k1cos а^)²+ (1 — cos а1У)

или с учетом выражения (17)

^1m^M(2(1+^k1^)R-k1^(S1^-S0⁾⁾²

Ei((2(1+ki)R-ki(Si-So))² + 2R(Si-So))-

Таким образом, получены расчетные формулы для определения характерных углов, определяющие такие характерные точки кривых контакта валков двухвалкового модуля, как начальная точка, конечная точка, точка максимальной деформации, точка, разделяющая зоны скольжения отставания от зоны прилипания, точка, разделяющая зоны прилипания от зоны скольжения опережения, нейтральная точка и точка максимума нормального напряжения.

ВЫВОДЫ

На основе анализа полученных расчетных формул характерных углов, выявлено:

• •    угол захвата и угол выхода зависят от начальной    и    конечной    толщины

обрабатываемого материала, расстояния между валками в начальном контакте и в установившемся режиме, а также от угла трения слоя материала о поверхности покрытия валка;

• •    угол максимальной деформации в двухвалковом модуле можно считать равным нулю;

• •    на величины углов, разделяющие зоны прилипания от зон скольжения,  влияют

внешние силы,  действующие на валок, угловая    скорость    валка,    скорость обрабатываемого материала, коэффициент трения, а также геометрические параметры обрабатываемого материала и валка;

• •  в приводном валке нейтральный угол

находится по направлению входа слоя материала в зоне контакта валка, в свободном валке – в направлении выхода;

• • точка максимума эпюр нормальных

напряжений не совпадает с нейтральной точкой и всегда находится в зоне сжатия.