Hashing Key Based Analysis of Polynomial Encryption Standard

Published Online November 2016 in MECS DOI: 10.5815/ijcnis.2016.11.05

The rapid development in information technology provided a way to transfer the data easily and safely over a communication network. But this development on the other hand, also created some challenging issues. Like, data security is a challenging issue of data communications today that covers many areas including secure communication channel, strong data encryption techniques and trusted third party to maintain the database. Therefore, it is necessary to apply effective techniques to enhance data security [1]. Cryptography is one such important technique for this purpose.

Cryptography is a term that mean “hidden secret”, is the practice and study of techniques for secure communication in the presence of third parties called adversaries. It is a three steps process as shown in Fig.1. At transmitter end, encryption is done i.e. original data (plain text) is converted into coded form (cipher text) while at the receiver end, decryption is done i.e. coded form (cipher text) is converted back into original data (plain text) [2].

Cryptographic techniques are classified into three categories as:

• a)    Symmetric-Key Cryptography:   Symmetric-Key

Cryptography refers to encryption methods in which sender and receiver both share the same key for encryption and decryption.

• b)    Asymmetric-Key Cryptography: Asymmetric-Key Cryptography refers to encryption methods in which paired keys are used. Public keys that may be broadcast widely paired with private keys which are known only to the owner.

• c)    Cryptographic Hash Function: A hash function is a mathematical computational function that takes a relatively arbitrary amount of input and gives an output of fixed size. The inputs to a hash function are termed as messages, and the outputs are often called as message digests [4, 5].

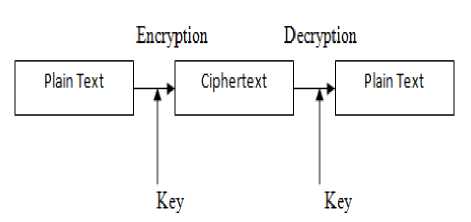
Fig.1. Block diagram of Cryptographic Process

Cryptographic Hash Algorithms are further classified as:

Message Digest (MD):

MD2 is a hash function that was published by R. Rivest of RSA Data Security Inc. in 1990 [4]. It uses a random 8-bit permutation and although it is software oriented, still it is not too active in software. Another algorithm by the same designer is MD4. This algorithm uses a standard 32-bit logic and arithmetic operations and is very effective in software. In event of some attacks, R. Rivest realized that the security level of MD4 was not as generous as he intended, and then he proposed a strengthened version of MD4 in 1991, named as MD5.

Secure Hash Algorithm (SHA):

SHA-1: The Secure Hash Algorithm (SHA) was initially permitted to use with the Digital Signature Standard (DSS) in 1993. After two years, the standard was updated, which is currently known as SHA-1. The first version of SHA is referred as SHA-0 in the cryptographic literature, although it has never been its official designation. SHA-1 is closely formed after MD4, taking some idea from MD5. It uses the same padding algorithm. The size of its internal state and its output length are 160 bits, which is considerably longer than MD5’s 128 bits.

SHA-2: The new standards were issued by NIST (n ational i nstitute of s tandards and t echnology ) in August 2002 add three members (SHA-256, SHA-384 and SHA-512) to the SHA family of functions, followed by one more (SHA-224) in 2004.

The connections between the NIST-approved functions are following: Both SHA-256 and SHA-512 have similar designs. SHA-256 operates on 32-bit words while SHA-512 operates on 64-bit words. Both designs bear strong alikeness to SHA-1, although they are much closer to each other than to their common predecessor.

SHA-384 is a trivial modification of SHA-512, which consists of compact the output to 384 bits and modifying the initial value of the chaining variable. A notice issued in February 2004 that defined SHA-224 as a truncated version of SHA-256 with a different initial value [6].

SHA-3: A hash function earlier called as Keccak, was released in 2012 after a public competition among non-NSA (National Security Agency) designers. It supports the same hash lengths as SHA-2, and its internal structure differs notably from the rest of the SHA family [7]. However there had not been any acknowledged attacks on SHA-2, NIST decided that launching an alternative to SHA-2 using a different algorithm would be careful.

The remainder of paper has been organised as follows:

The related work is highlighted in section II, followed by proposed methodology in section III. The result and conclusion is presented in section IV and V respectively.

• II.    Related Works

In this section, a brief introduction of the related works or the work which is taken as the base for the implemented work is presented, which is essential in the understanding of the remainder of the paper. Many researchers have published their work on the comparison of different hash functions based on different parameters. As the work is implemented using hash function such as SHA-1 and SHA-256 with polynomial message authenticating scheme. The contribution of some of researchers on related works is presented as follows:

W. Zhang et al. [8] have presented a work as lightweight and compromise-resilient message authentication in sensor networks. Author proposed a novel message authentication approach which adopts a perturbed polynomial-based technique to simultaneously accomplish the goals of lightweight, resilience to a large number of node compromises, immediate authentication, scalability, and non-repudiation.

K.K. Raghuvansi et al. [9] have presented a work on study and comparative analysis of different hash algorithm. Author has implemented Hash Algorithms and has compared them on the basis of time, avalanche effect and space.

Piyush Gupta et al. [10] have presented a work on comparative analysis of SHA and MD5 algorithm. Author provided the comparison based on the time taken to build a hash as well as it also compares the bit rate passes through a hash value.

R. Roshdy et al. [11] have presented a work on design and implementation a new security hash algorithm based on MD5 and SHA-256. Author provided a proposal for a new secure hash algorithm based on the combination of some functions of SHA-256 (Secure Hash Algorithm 256) with its message expansion modification and MD5 (Message Digest 5) based on double-Davis-Mayer scheme to overcome the weakness existing in these functions.

Piyush Garg et al. [12] have reviewed the performance analysis of SHA algorithms (SHA-1 and SHA-192). There are many secure hash algorithms are available. All these algorithms are iterative, one-way hash functions to produce a message that can process for condensed representation called a message digest.

The existing algorithms enable the message’s integrity for messages: there is high probability that any change to the message, results in a different message digest. For the authentication codes and verification of digital signatures, this property is very useful, and also in the random numbers (bits) generation. The existing algorithms differ mostly in the number of bits of security that are provided for the information being hashed this is directly related to the message digest length.

When an existing secured hash algorithm is used in conjunction with other algorithm, there may be requirements specified elsewhere that require the use of an existing secured hash algorithm with a certain number of bits of security. Author presented the combined study of SHA-160 and SHA-192 algorithm. Experimental results are presenting overall observation of these two algorithms

• III.    Proposed Methodology

In this, a new model is presented in which hashing algorithm SHA-1 and SHA-256 is implemented with polynomial message authenticating scheme and comparative analysis of both the SHA-1 and SHA-256 is done. The following parameters are considered in the presented work.

• Polynomial Function:

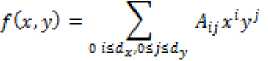
• •    Hashing Algorithm: SHA-1 and SHA-256

• •    Hash Code length: 24, 32, 40 and 64 bits

• •    Polynomial degree: 80,100 and 150

• •    Parameters for Comparison: Processing Gain, Delivery Ratio, Energy consumed and Duty Cycle

• A.    Proposed Model:

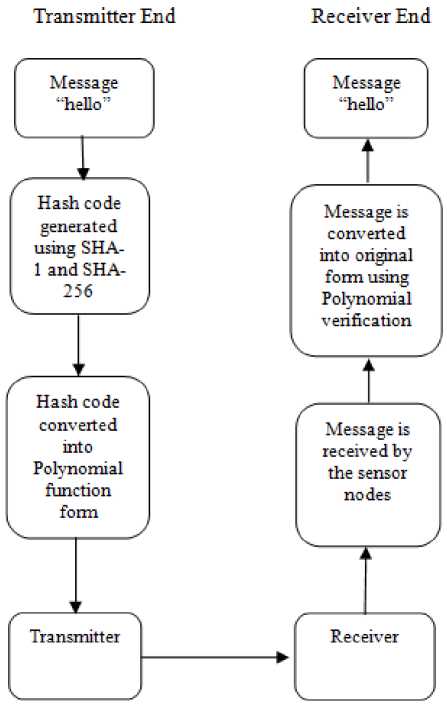
Fig.2. Flow of Designed Model

• B.    Working Methodology

Step I: At transmitting end, firstly, Message or data is taken which is transmitted from transmitter to receiver. In the presented work “hello” message is used.

Step II: The message is converted into cryptographic hash code by using SHA-1 or SHA-256, Secure Hash Algorithm. The hashing length of code is taken 24, 32, 40 and 64 bits.

Step III: Then the hash code is converted in the form of polynomial function by using the two variable polynomial function used in Polynomial Message Authenticating Scheme. The Polynomial function used in presented work with degree 80, 100 and 150.

Step IV: At the end, the Polynomial based code is given to the transmitter which transmits it to the receiver over a network.

Step V: At receiving end, message is retrieved into original form using polynomial message verification scheme. In polynomial message authenticating scheme, each sensor node or receiving system is assigned an identification number which helps in authorized reception of message.

• IV. Experimental Results

The proposed method not only provides high security but also gives a comparative analysis of SHA-1 and SHA-256 on the basis of different parameters. Following graphical representation shows the parameter value with respect to security level.

Comparative analysis of SHA-1 and SHA-256 is done on the basis of following parameters:

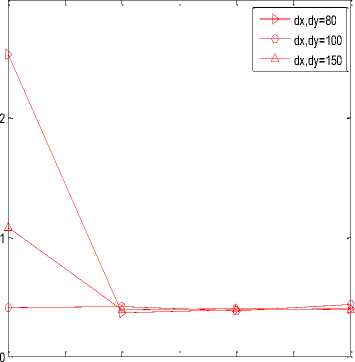
Processing Gain

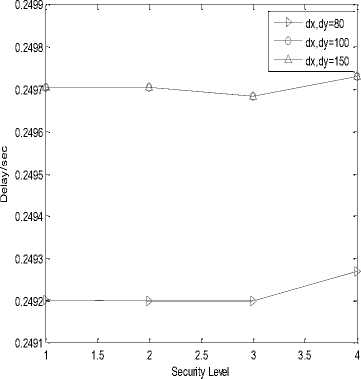
It is the total time taken in conversion of message from its original form to polynomial based form. Total time taken from step- 1 to step- 3 constitute total processing gain. It is individually measured at both transmission end and reception end. At transmitter end time is measured in conversion of message from original form to polynomial based form. While at receiver end reverse process is follows i.e. total time taken in conversion of polynomial based code to original message is measured. The presented work is showing the result in delay/sec.

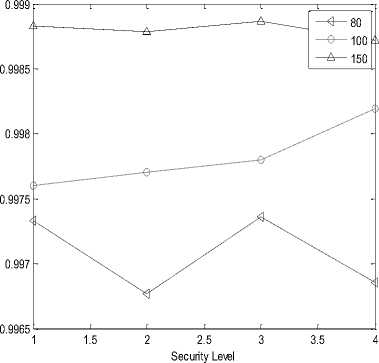
Delivery Ratio

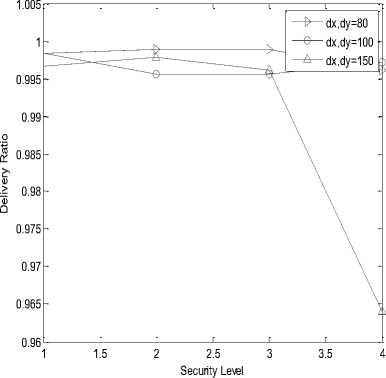
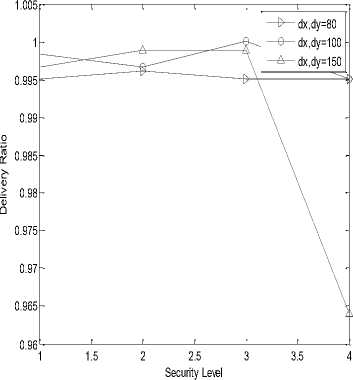
It is the probability of message transmission and message reception from transmitter to receiver. The variation in the value of probability of transmission and reception of message is measured for 24, 32, 40 and 64 bits length of Hash Code and for Polynomial Function with degree of 80, 100 and 150. The delivery ratio is measured at both ends i.e. transmitter and receiver.

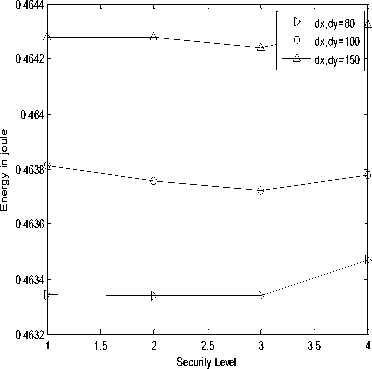
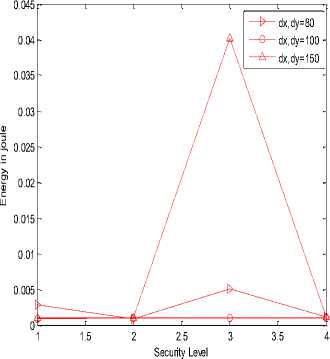
Energy Consumed

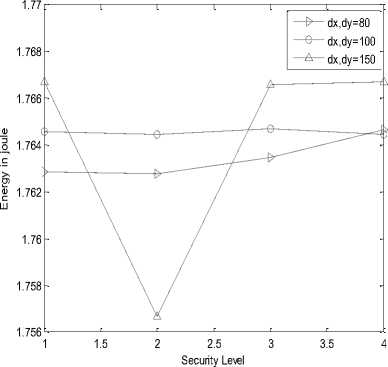
It is measured in joule. It is the amount of energy used by the system in the conversion of message from original form to polynomial based form and also in reverse process that is at the reception end. It can be said that energy consumed by the system in the conversion process is directly proportional to the time taken in conversion and transmission process. Energy consumed is measured at both ends.

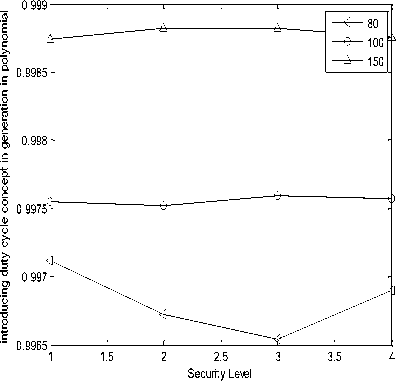
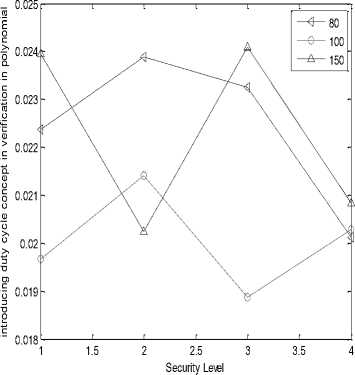
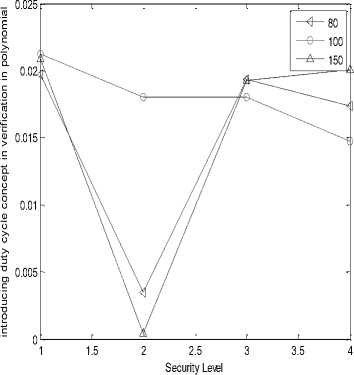
Duty Cycle

It is measured as processing time over total time taken by the process or the system. Duty Cycle basically represented as the processing or working time of the system over the total time taken by the system in both cases that is processing time and idle time. Idle time represents a state of no working situation. It is also measured at both transmission and reception ends.

In the following simulation results, X-axis is representing security level or hashing length i.e. value 1, 2, 3 and 4 are representing 24, 32, 40 and 64 bits of hash code length respectively. Graph (a), (b), (e), (f), (i) and (j) are represented on ¼ scale.

(a)

(b)

(c)

(d)

(e)

(f)

introducing duty cycle concept in generation in polynomial

(g)

(h)

-4 x 10^-4

1          1.5          2          2.5          3          3.5          4

Security Level

(i)

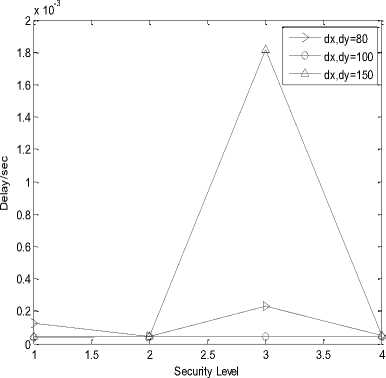
(j)

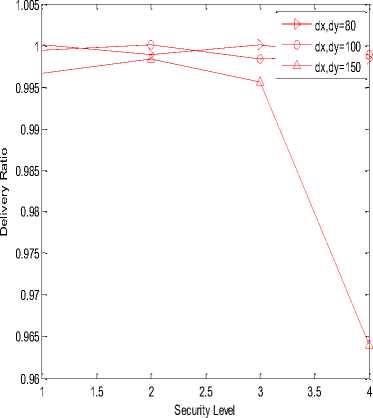
(k)

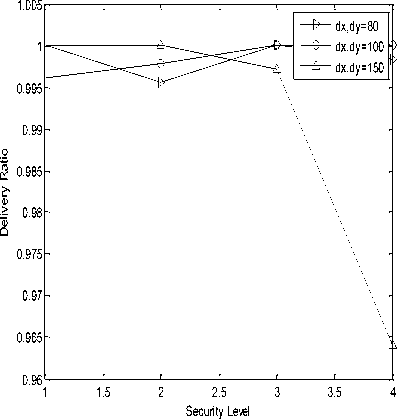
(l)

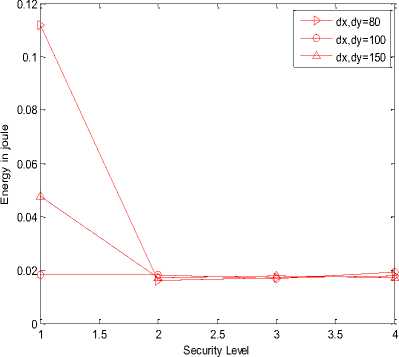
(m)

(n)

(o)

(p)

Fig.3. (a) Processing gain of SHA-1at transmitter;(b) Processing gain of SHA-256 at transmitter;(c) Delivery ratio of SHA-1 at transmitter;(d) Delivery ratio of SHA-256 at transmitter;(e) Energy consumed in SHA-1 at transmitter;(f) Energy consumed in SHA-256 at transmitter;(g) Duty cycle of SHA-

1 at transmitter;(h) Duty cycle of SHA-256 at transmitter;(i) Processing gain of SHA-1at receiver;(j) Processing gain of SHA-256 at receiver;(k) Delivery ratio of SHA-1 at receiver;(l) Delivery ratio of SHA-256 at receiver;(m) Energy consumed in SHA-1 at receiver;(n) Energy consumed in SHA-256 at receiver;(o) Duty cycle of SHA-1 at receiver;(p) Duty cycle of SHA-256 at receiver

Comparative Analysis:

Table 1. Comparative simulation results of SHA-1 and SHA-256 at Transmitter (Encryption end)

Hash Code length (bits)	Polynomial Degree: 80
	Parameter Measured
	PG		DR		EC		DC
	SHA-1	SHA-256	SHA-1	SHA-256	SHA-1	SHA-256	SHA-1	SHA-256
24	0.9968	0.9968	0.9983	0.9950	7.0516	1.8534	0.9961	0.9971
32	0.9970	0.9968	0.9989	0.9961	7.0520	1.8534	0.9973	0.9967
40	0.9956	0.9968	0.9989	0.9950	7.0540	1.8534	0.9968	0.9965
64	0.9969	0.9971	0.9961	0.9950	7.0572	1.8539	0.9974	0.9969
	Polynomial Degree : 100
24	0.9979	0.9978	0.9983	0.9983	7.0592	1.8552	0.9976	0.9975
32	0.9978	0.9977	0.9956	0.9967	7.0592	1.8550	0.9976	0.9975
40	0.9978	0.9976	0.9956	1	7.0600	1.8549	0.9977	0.9976
64	0.9980	0.9977	0.9972	0.9950	7.0596	1.8559	0.9978	0.9976
	Polynomial Degree : 150
24	0.9989	0.9988	0.9967	0.9967	7.0672	1.8571	0.9989	0.9987
32	0.9988	0.9988	0.9978	0.9989	7.0252	1.8571	0.9988	0.9988
40	0.9988	0.9987	0.9967	0.9989	7.0672	1.8570	0.9988	0.9988
64	0.9990	0.9989	0.9640	0.9640	7.0676	1.8573	0.9989	0.9988

Table 2. Comparative simulation results of SHA-1 and SHA-256 at Receiver (Decryption end)

Hash Code length (bits)	Polynomial Degree: 80
	Parameter Measured
	PG		DR		EC		DC
	SHA-1	SHA-256	SHA-1	SHA-256	SHA-1	SHA-256	SHA-1	SHA-256
24	0.0010	0.51403	1	1	0.4469	0.0114	0.0224	0.0197
32	0.14628	0.16485	0.9989	0.9956	0.0644	0.0037	0.0239	0.0035
40	0.15625	0.91438	1	1	0.0688	0.0203	0.0233	0.0194
64	0.16077	0.91570	0.9983	0.9983	0.0708	0.0042	0.0201	0.0174
	Polynomial Degree : 100
24	0.16304	1.5625	0.9994	0.9961	0.0718	0.0035	0.0197	0.0212
32	0.16576	1.7527	1	0.9978	0.0730	0.0039	0.0214	0.0180
40	0.15217	1.8115	0.9983	1	0.0670	0.0040	0.0189	0.0180
64	0.17300	1.8025	0.9989	0.9950	0.0761	0.0040	0.0203	0.0147
	Polynomial Degree : 150
24	0.43205	1.7481	0.9967	1	0.1902	0.0039	0.0240	0.0209
32	0.15579	1.7844	0.9983	1	0.0686	0.0040	0.0202	0.4373
40	0.16123	0.0073	0.9956	0.9972	0.0710	0.1608	0.0241	0.0192
64	0.15534	1.9338	0.9640	0.9640	0.0684	0.0043	0.0201	0.0201

Comparative Analysis

• 1.    Transmitter End

• •    The Processing Gain of SHA-1 is higher than SHA-256 for higher degree polynomial i.e. 100 and 150.

Whereas, at low degree polynomial Processing Gain of SHA-1 is less.

• •    The Delivery Ratio of SHA-256 is higher than SHA-1 for higher hashing length and higher polynomial degree. Whereas, at low degree polynomial Delivery Ratio of SHA-1 is high.

• •    The Energy Consumption of SHA-1 is much higher than SHA-256 for all hashing length and polynomial degree.

• •    The Duty Cycle of SHA-1 is higher than SHA-256 for all hashing length and polynomial degree.

• 2.    Receiver End

• •    The Processing Gain of SHA-256 is higher than

SHA-1 for all polynomial degree and hashing length.

• •    The Delivery Ratio of SHA-256 is higher than

SHA-1 for higher polynomial degree i.e. 150.

Whereas, at low degree polynomial i.e. 80 and 100 Delivery Ratio of SHA-1 is high.

• •    The Energy Consumption of SHA-1 is much higher than SHA-256 for all hashing length and polynomial degree.

• •    The Duty Cycle of SHA-1 is higher than SHA-256 for all hashing length and polynomial degree

• V. Conclusion

In the proposed model, Cryptographic Hash algorithms with Polynomial message authenticating scheme has been implemented with MATLAB as the processing tool. This method provides high security level. The algorithm SHA-1 and SHA-256 implemented with polynomial scheme has been compared based on the parameters like processing gain, delivery ratio, energy consumed and duty cycle. Above tables summarizes that the comparative result for SHA-1 and SHA-256 represents that SHA-1 has higher processing gain, energy consumption and duty cycle as compare to SHA-256 while SHA-256 has higher delivery ratio as compare to SHA-1. So, it is concluded that SHA-256 is better than SHA-1 based on the considered parameters.