High Resolution Identification of Wind Turbine Faults Based on Optimized ESPRIT Algorithm

Published Online April 2015 in MECS DOI: 10.5815/ijigsp.2015.05.04

Wind energy has become one of the popular renewable powers all over the world in electricity generation capacity. Wind turbines contain a complex electromecanical system which is prone to defects. Consequently, there is an increase need to implement a predictive monitoring scheme of wind turbines, allowing an early detection of electromechanical faults, in order to avoid catastrophic damage, to reduce maintenance costs, to ensure continuity of production and to minimize downtime. It means that stopping a wind installation for unexpected failures could lead to expensive repair. These faults cause a modulation impact in the magnetic field of the wind generator, which is characterized by the appearance of a significant harmonics (peaks) in the stator current spectrum. For this reason, most of the recent researches have been oriented their interest toward electrical monitoring, with focus on frequency analysis of stator current (CSA). This technique is more practical and less costly [1], [2], [3], [4], [5]. Furthermore, with recent digital signal processor (DSP) technology developments, motor and generator fault diagnosis can now be done in real-time [1]. ESPRIT is one high resolution or subspace method (HRM) which is widely adopted in electromechanical machine diagnosis. It can be used for spectral estimation [4], [6], [7]. This algorithm allows very high spectral detection accuracy and a high resistance to noise compared to others methods like MUSIC and Root-MUSIC. Contrariwise, it require long computation time to find more frequency estimates when the autocorrelation matrix is large and the order of sampled data dimension increase. This fact makes its application in real time detection very limited despite its high precision. This article presents an ameliorated version of ESPRIT-TLS method for fast wind turbine faults detection and diagnosis based on a band pass filtering technique. The proposed improvement allows many advantages: reduction of computation time, saving of memory space and accuracy increase in a specified frequency bandwidth. The paper is organized as follows: the problem is formulated in section2, the stator current signal is presented in section3, and then section4 describes wind turbine fault models. While section5 focuses on ESPRIT method theory, section6 explains in details the proposed approach to enhance original ESPRIT algorithm. Simulation results are presented and discussed in Section7. Finally, conclusions with future work are drawn in the last section.

• II.    Related Work

Many research studies applying enhanced and advanced signal processing techniques have been used in the motor and generator stator current to monitor and to diagnose prospective electromechanical faults. The classical methods like periodogram and its extensions which are evaluated through a Fast Fourier Transform (FFT) are not a consistent estimator of the PSD because its variance does not tend to zero as the data length tends to infinity. Despite this drawback, the periodogram has been used extensively for failure detection in research works [5], [7]. The (FFT) does not give any information on the time at which a frequency component occurs. Therefore, the Short Time Fourier Transform approach (STFT) is used to remove this shortcoming. A disadvantage of this approach is the increased sampling time for a good frequency resolution [8]. The discrimination of the frequency components contained within the signal, is limited by the length of the window relative to the duration of the signal [9]. To overcome this problem, in [10] and in [11] Discrete Wavelet Transform (DWT) is used to diagnose failures under transient conditions for wind energy conversion systems by analyzing frequencies with different resolutions. This method facilitates signal interpretation because it operates with all information contained in the signal by timefrequency redistribution. One limitation of this technique that it gives a good time resolution and poor frequency resolution at high frequencies, and it provides a good frequency resolution and poor time resolution at low frequencies [5], [12]. Recently, high resolution methods (HRM) are applied to detect more frequencies with low SNR. In fact, MUSIC and ESPRIT techniques with its zooming extensions are conjugated to improve the identification of a large number of frequencies in a given range [13], [14]. In [15] a comparative performance analysis of (HRM) is made. This study has demonstrated that ESPRIT method has a high accuracy which exceeds all other algorithms even with the existence of an annoying noise. Moreover, these algorithms are based on an eigenanalysis of the autocorrelation matrix of a signal corrupted by noise. This decomposition requires a long computation time mainly when the size of the autocorrelation matrix and the number of data samples increase. In [16] a rank reduced ESPRIT technique is proposed to transform it into simplified low-complexity algorithm. However, this method presents performance deterioration mainly with the SNR decreasing and lowers harmonic amplitudes. Moreover, it has not focused on the minimization of the computational time execution for real applications. This work proposes a solution to overcome the complexity cost of ESPRIT in the purpose of its use in a real time wind turbine monitoring.

• III.    Stator Current Model

The application of CSA technique for diagnosis of wind turbine machine requires a well previously knowledge of various frequency and amplitudes components in stator current spectrum stemmed from the wind turbine generator in both healthy and faulty states. In fact, to build a correct detection of the wind turbine fault modulations and signatures in the stator current, it is necessary to construct a complex signal associated with the real one. This analytical signal model describes precisely the behavior and the evolution of the real stator current. It contains relevant fault information. For these reasons it is often used for command purposes. The studied wind generator stator current will be denoted by the discrete signal i[n]. This signal is considered as a sum of L complex sinusoids and white noise. It is obtained by sampling the continuous time current every Ts=1/Fs seconds. The induction generator stator current i[n] in presence of mechanical and/or electrical faults has a data model which can be expressed as follows [11]:

L     / 2 n . —. n + №

i [ n ] = Z Ike 1  Fs k=1

+ b [ n ]

Where i [ n ] corresponds to the nth stator current sample with n=0, 1, 2... N s -1. I k , f k , and φ k are the amplitude, the frequency and the phase of the k^th complex sinusoid (harmonic components) respectively, b [ n ] is a gaussian white noise. F_s is the sampling frequency and N_s is the number of data samples. L represents the number of researched harmonics.

• IV.    Wind Turbine Fault Models

The wind machine is susceptible to diverse electromechanical anomalies that involve mostly five components: the stator, the rotor, the bearings, gearbox and/or the air gap (eccentricity) [17]. These defects require a predictive recognition to avert any side effect provoking a breakdown or a fatal spoilage. Because it contains the totally relevant fault information, the stator current spectrum is examined to withdraw the sideband frequency components inserted by the fault. These fault frequencies are located around the fundamental line frequency and are called lower sideband and upper sideband components. This detection technique is used in collaboration with one bit vibration sensors for an early identifying of prospective electromechanical failures which can occurs in any time. A synopsis of wind turbine faults and their related frequencies formulas are presented in table1.

Table 1. Wind Turbines Faults Signatures

Failure	Harmonic Frequencies			Parameters
Broken rotor bars (brb)	Lb = f 0	, ( 1 - s Y k --- ± s _ к P J		k = 1,3,5,...
Bearing damage (bng)	Lg =| f 0 ± kf„\			k — 1,3,5,... [ 0.4 nhfr br • o - [ 0.6 n f
Misalignment (mis)	f mis =| f 0 ± kf„\			k — 1,3,5,...
Air gap eccentricity (ecc)	Lt = f 0	( 1 - s ) 1 ± m --- _     к P )_		m — 1,2,3,...

Where f ₀ is the electrical supply frequency, s is the perunit slip, P is the number of poles, f r is the rotor frequency, n_b is the bearing balls number, f _i,o is the inner and the outer frequencies depending on the bearing characteristics, and m, k ∈ ℕ are the harmonic frequency index [5], [10], [11]. Slip s is defined as:

ш - ш

S = —---

Ш ш = 12f sP

ω s is the generator synchronous speed,

ω r is the relative mechanical speed of the generator,

These harmonics are extensively used as diagnostic measures in the csa approach.

‘ N - M +1

Where M is the data matrix order and D is a Hankel data matrix defined by:

■ i ( 0 )         i ( Ns - M )"

D = Z \          X(9)

[ i ( M - 1 )    •    i ( N s - 1 ) J

• V. ESPRIT Method Theory

High resolution methods are recently used for fault diagnosis. They can detect and identify the faulty element based on its frequency. The most accurate and efficient technique is ESPRIT which belongs to the subspace parametric spectrum estimation methods. It is based on eigenvector decomposition which aims to separate the observation space in a signal subspace, containing only useful information, and its orthogonal complement, called noise subspace. The rotational invariance between both subspaces allows extracting of the parameters of spectral components present within the investigated waveform [18], [19], [21].

• A. Autocorrelation Matrix Estimation

Based on the stator current model defined by the equation (1), the autocorrelation matrix can be then estimated as follow [20]:

It is composed by the sum of signal and noise autocorrelation matrices. Where H is the Hermitian transpose, σ_b² is the variance of the white noise, I is the identity matrix of size ( N s x N s ) and P is the power matrix of the harmonics:

The dimension of R i should be high enough to have more eigenvalues for noise space and should be low enough to minimize the computation time cost. When the value of M decreases below N s /3, it can be seen the increase of the frequency detection error. Contrariwise, if M increases beyond N s /2, calculation time increases. So, there is a trade-off for the right choice of M . Empirically, the value of M is chosen to be bounded as shown in (10) to give a good performance:

N

N

In this paper, the autocorrelation matrix dimension M is taken rounded down as follows:

M = Round

—

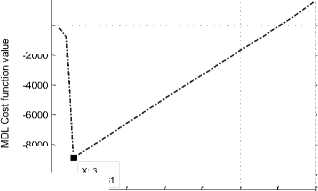
Evidently, the number of frequencies L is not a priori known. The frequency signal dimension order (FSDO) L must to be estimated by the minimization of a cost function MDL ( k ) named minimum description length. In order to obtain a robust estimate, (MDL) criterion is used as shown in the following formula [19] for k=1, 2,…, L :

P = diag [ 1 2 12- --Il J                   (5)

MDL ( k ) = - log

S is the Vandermonde matrix defined by:

r

П AL‘ i=k+1___________

L

A

I L - k , ^ 1 i

p ( L - k )

⁺ 2 k ^{( 2 L - k} ) ^{log( p )}    (12)

S k =

S = [ s_rs^^ ]

P = N s - L - 2

j 1 2 , . F ]   j [ 4 . .F ]      j [ _M N -

1 e ^{v s v} e ^{v s v} • ee ^v             s'

Where λ_i are eigenvalues autocorrelation matrix R_{i .} Analytically, the estimate of L can then be expressed in the form:

The finite data length of the signal makes the computation of the autocorrelation matrix Ri inaccurate For real purpose, this matrix is unknown and it must be singular For effective detection, it is necessary to reduce the statistical fluctuations present in estimating the autocorrelation matrix by the averaging [8], [20] In addition, the accuracy of ESPRIT depends on the dimension (M ≤ Ns) of Ri It is possible to estimate it from the acquired data samples by the following relationship [8], [20]:

T v = arg^ min ( MDL ( k ) )

However, ESPRIT performances are completely degraded by choosing a wrong FSDO value.

• B.    Eigendecomposition of autocorrelation matrix

The eigendecomposition of the autocorrelation matrix R i is given by exploiting the eigenvalues { λ 1 , λ 2 , …, λ M } and their corresponding signal eigenvectors { v 1 , v 2 , …, v M } [18]:

Where:

N s

R = ЁЛ vV i     kkk k=1

= UEU + U b -E b Ub^

R s R b

Once the searched frequencies components of the signal are estimated by ESPRIT, the values of their amplitudes and then their powers can be estimated. By using the eigendecomposition of the subspace signal [18], [20]:

^U s = [ v r ■ V ] , ^E , = diag [ Л • ”4 ]

^U b = [ ^V L + 1 "  " ^VN, J , ^E b = ^b I N, - L

L

R = S . P. S^H = У Л + ^,Л^ v H k = 1

U s represents the eigenvectors matrix of the signal space related to the L largest eigenvalues arranged in descending order. Whereas, U b represents the eigenvectors matrix of the noise space related to the N s -L eigenvectors that, ideally, have eigenvalues equal to the variance noise σ b ² . Diagonal matrices E S and E b contain eigenvalues λ i corresponding to eigenvectors v i .

• C.    Frequency Estimation

ESPRIT method is based on the study of the signal subspace E_s . It uses some rotational invariance properties founded naturally in the case of exponential. A decomposition of the matrix S into two matrices S 1 and S 2 is considered as follows:

It is assumed that the eigenvectors of the signal subspace are normalized as follows:

vH -vk = 1

Thus, for k=1, 2,…, L :

Ri-vk = ^k -vk(24)

Multiplying both sides of this equation by v k ^H:

vk -Ri-vk = ^k-vk -vk(25)

S =

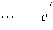
S 1

S 2

According to (4), (11) and (21):

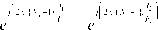
v H - R i -V k = v H -

Г

Z ^Pk^sk^sk ⁺ ^ b -I - ^Vk = ^ k

_ k = 1                      _

S 1 represents the first N s -1 rows of the matrix S

S 2 represents the last N s -1 rows of the matrix S

The rotational invariance between both subspaces leads to the equation:

This equation can be simplified as follows:

L ₂

Z ^Pk ^-I s k ^{- V}k\ = ^ k - ^ b                (27)

k =1                                                         ^{V 7}

S = Ф S₂

Using the following equation:

The matrix Φ contains all informations about L components frequencies. Nevertheless, the estimated matrices S can contain errors. Thereafter, the ESPRIT-TLS (total least-squares) algorithm finds the matrix Φ by minimization of matrix error given by [21]:

	е '2 ' ^ ’
		0	0
Ф =	0	(2 ’ 1} e v      s 7     •	0	(20)
	_    0	0	e Ki_

The determination of this matrix can lead to obtain the frequency estimates defined by this formula:

,   Arg (Фk,k )„ ,   10 у fk =    2n ’F, k = 1,2,-,L            (21)

• D.    Harmonics Powers Estimation

I , H v . ) = ^ . ( e^{2 4})|¹

Equation (22) can be written in the following expression:

L ₂

Z P k -I Q k ( e^{j2 nt} ) = л . - ^ 2            ₍₂₉

This equation is a set of L linear equations with a number L of unknown harmonics powers. It is very easy to extract the harmonics powers vector P from the equation (25) by simple resolution.

• VI.    Improved ESPRIT Method

The discrimination of all small amplitude frequency components around f0 by ESPRIT method is difficult. This is mainly due to the significant computation time elapsed by this algorithm to find harmonic sideband components correctly. Furthermore, ESPRIT calculation cost increases when the size of the autocorrelation matrix and the number of data samples increase. It depends on the complexity of Ns3. This delay forms a major drawback that can cause a catastrophic evolution of a wind turbine fault which may lead to greatest damages. In order to apply a proactive, robust and real time wind turbine condition monitoring, an improved version of ESPRIT algorithm entitled Fast-ESPRIT was used. Figure 1 shows the block diagram scheme of different stages that Fast-ESPRIT algorithm must execute to identify the fault harmonic frequencies and their powers.

Three Phase Stator Current i1(t)

i 3 (t)

i 2 (t)

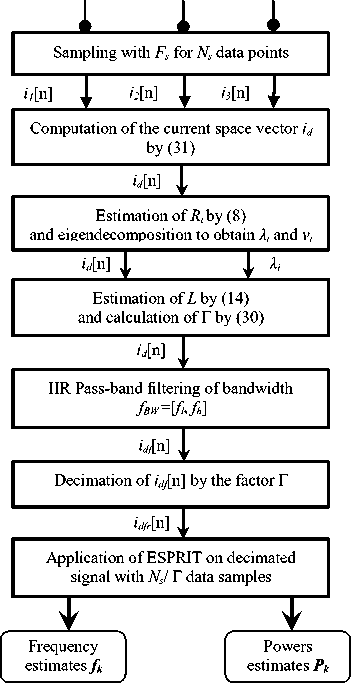
Fig 1. Block diagram scheme of the Fast-ESPRIT algorithm

The ameliorated algorithm is based on both a bandpass IIR filtering and decimation technique in the fault frequency bandwidth [ f_l , f_h ], where f_l , f_h are the low cutoff and high cut-off frequency of the band-pass filter. This process provides a remarkable reduction in computation time and in data memory size. The decimation factor used in this research is computed with respect to the Nyquist criteria as follows [22]:

г = ^

F

N = -F- if f_h <  95 Hz 2 f 0 4 f 0 ^h

F

N = -F- if 95 Hz <  f <  500 Hz

6 f 0 12 f 0                 ^h

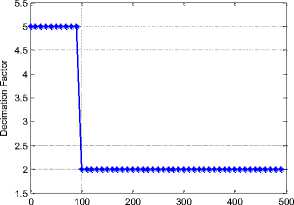
Figure 2 shows the variation of Г according to f_h . The decimation factor decreases with the increase of the maximum harmonics frequency detected in the signal.

High cut-off frequency [Hz]

Fig 2. Evolution of decimation factor with fault frequency

In the first time, the acquired sequences i_1,2,3 [ n ] of the three phase stator current sampled at the frequency F s , are used to calculate the stator current space vector as follows [23]:

2 •                   .2 ^

i + a.i, + a i        з— id = -1------2;-------3, a = e

Where a , a² are the spatial operators. This vector allows a fault diagnosis on all phase stator current instead of examining fault signature on each ones. With this method computation time will be minimized. In the second step, an estimation of the autocorrelation matrix R i is realized and therefore the eigenvalues λ i are extracted to estimate the number of researched harmonics L in the stator current signal with respect to MDL criterion seen in (14). Then, the signal sequence i_d [ n ] is filtered via a recursive Infinite Impulse Response (IIR) digital band-pass filter based on a least squares fit in the frequency range [ f_l , f_h ] characterizing the fault. This filter has a flat response in the desired bandwidth and its use is justified by the fact that it will be helpful to extract just the informations contained in the signal which are useful in the fault recognition which can occurs at any time. In the third stage, the received sequence of the stator current space vector i df [ n ] is decimated by a factor Г shown in (30). In addition, the applied decimation uses low-pass filter to ensure anti-aliasing. The motivation for this decimation is to reduce the cost processing and memory required for a cheaper implementation. Finally, the ESPRIT algorithm is applied on the decimated signal sequence having N_s /Г data samples to identify all frequency components and their powers contained in the signal.

• VII.    Simulation Results and Analysis

The developed approach seen in the previous section has been applied and simulated under different scenarios of wind turbine fault types shown in table 1. To evaluate its performance in real time fault detection, Fast-ESPRIT algorithm has been integrated with a fault diagnosis controller which coordinates with vibration sensors localized in specific wind turbine mechanical components to monitor vibration levels. The controller decides and classifies the existence of a fault depending on vibration measurements collected by the sensors and the harmonic frequencies with their powers estimated by the Fast-ESPRIT method. Figure 2 illustrates the explained technique. Besides, the applied diagnosis algorithm is based on the use of a fault frequency band switching which sweeps any prospective faults that may occur and subsequently classify them by type according to their frequencies. Thus, the diagnosis is made by the intervals of the spectrum reflecting the signature of a possible default [24], [26]. This means that the Fast ESPRIT method will not be applied to the entire signal but only on a part that contains the target information to be extracted for analysis. In case of fault detection, a system alarm is triggered to alert monitoring and maintenance staff for an emergency intervention repair.

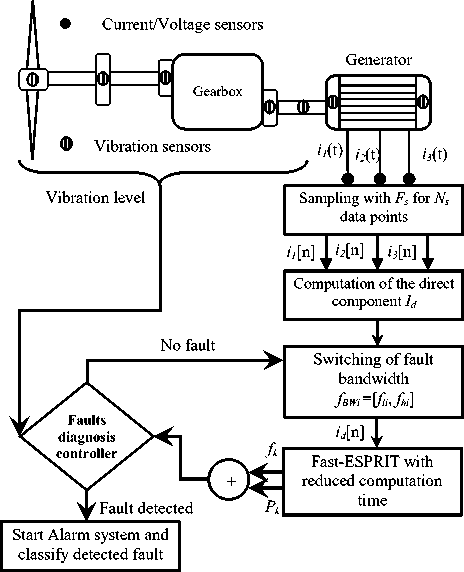
Fig 3. Intelligent wind turbine faults diagnosis by Fast-ESPRIT

This procedure provides many benefits because it allows high recognizing and classification of faults with economic and real time implementation [25]. Computer simulations are realized in Matlab for a faulty wind turbine generator using 2 pair poles, 4kW/50Hz, 230/400V. The induction generator stator current, is simulated by using the signal model described in (1) for the different failure kinds described in table 1. The parameters of the simulations are illustrated in table 2.

To simplify the simulation, a single phase of the generator stator current has been studied. The power of each fault is calculated based on its amplitude as follows:

P k = 1^0log 10

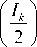
Before examining the stator current signal, it must be filtered to obtain in the output a composite signal having a totally negligible noise compared to the fundamental and its harmonics.

Table 2. Parameters used in the simulations

Parameter	Value
s	0,033
P	2
f 0	50 Hz
f r	29,01 Hz
n b	12
N s	1024
F s	1000 Hz
Fundamental Stator Current Amplitude	10 A
Computer Processor	Intel Core2 Duo T6570 2,1 GHz

• A.    Air gap eccentricity detection

Table 4 shows the simulation results for identifying wind turbine generator air gap eccentricity fault signature in the goal to compare the performance of the original ESPRIT-TLS with the proposed Fast-ESPRIT. The harmonics characterizing this fault are given by table 3.

Table 3. Air gap eccentricity fault parameters

f ecc (Hz)	I ecc (A)	P ecc (dB)	N h	SNR (dB)
25.825 74.175	0.4 0.3	-10.97 -13.46	3	80

This experiment was done with a high signal to noise ratio to determine the computing time and the required memory size in both algorithms.

Table 4. Computation performance comparison

Met hod	Data sample s	Harmonics f k / P k	Signal Memor y size (KB)	M	Time (s)
Ori gina l ESP RIT	1024	50.00Hz/ 16.99dB 25.82 Hz/ - 10.97dB 74.17Hz/ - 13.47dB	16	511	4.3471
Fast ESP RIT	205	49.99Hz/ 16.96dB 25.81Hz/ - 12.10dB 74.17Hz/ - 14.12dB	3.2	102	0.03046

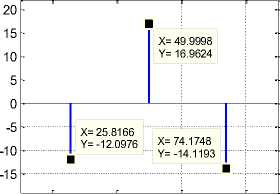
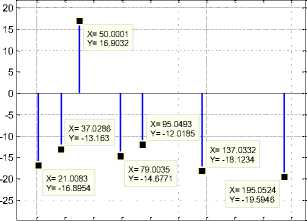
It is very clear from table 4 that both original and fast ESPRIT algorithms provide satisfactory accuracy, and they correctly identify the L=3 harmonics despite with smallest powers case. The little performance difference observed in the Fast- ESPRIT is justified by the attenuations caused by the IIR band pass filter used. Furthermore, the obtained results confirm the important reduction of the computational time with 142.7 times, the memory size required for processing with 5 times and complexity has been changed from N s ³ to ( N s /Г)³.

-2000

-4000

-6000

-8000

-10000

X: 3

Y: -8881

0      5     10     15     20     25     30     35

Fig 4. Estimation of signal harmonics number by MDL criterion

In addition, a negligible performance loss is observed in the power and frequency estimation caused by the band pass filter attenuations. Figure 4 illustrates the estimation of the signal subspace dimension by means of the Rissanen criteria based on MDL function cost shown in (12) and (14). Figure 5 shows the frequency response gain of the Yule-Walk IIR band pass filter used in the Fast-ESPRIT algorithm having an order h=25. Obviously, the filter has a flat response in the bandwidth target.

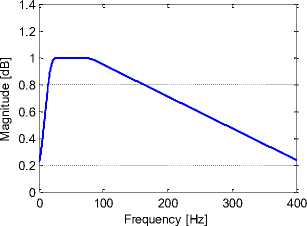
Fig 5. IIR filter Yule-Walk frequency response gain

Whereas, figure 6 illustrates graphically the power and frequency estimates given by the proposed method. It seems obviously that Fast-ESPRIT has detects all harmonics existents in the eccentricity fault range [20, 80]Hz with high precision.

20       40       60       80

Frequency [Hz]

Fig 6. Power and Frequency estimates by Fast-ESPRIT for eccentricity fault

• B.    Broken rotor bars detection

The proposed Fast-ESPRIT method has been applied for a wind turbine generator stator current to detect broken rotor bars fault signature in the frequency range [15, 80]Hz. The characteristics of this fault harmonics are shown in table 5. The obtained results are averaged over fifty realizations.

Table 5. Broken rotor bars fault parameters

f brb (Hz)	I brb (A)	P brb (dB)	N h	SNR (dB)
22.525	0.3	-13.47
25.825	0.45	-9.95	5	20
70.875	0.35	-12.13
74.175	0.4	-10.97

From Figure 7, the Fast ESPRIT method flows a large calculation time with a large average estimation error rate for discriminating the fault harmonics and their powers contained in a very noisy stator current signal having SNR value less than or equal to 15dB. This can be interpreted by the delays caused by the algorithm search to find the eigenvalues and eigenvectors of the autocorrelation matrices in both signal and noise spaces. Contrariwise, the calculation time in question decreases gradually for a slightly noisy signal with SNR>15dB. The average estimation error declines also to fall to a minimum value for large values having SNR>55dB.

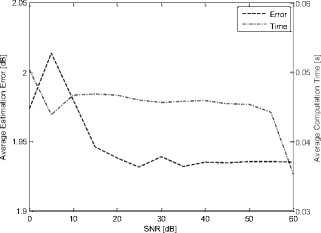
Fig 7. Evolution of fault powers estimation error and computation time with SNR

The method finds difficulty in identifying faults in a very noisy environment. As shown in figure 8, for a stator current signal with a high annoying noise SNR<10dB, detection fault powers presents a considerable error and a remarkable instability level.

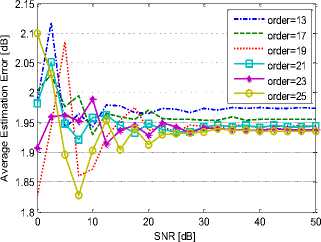
Fig 8. Variation of fault powers estimation error depending on IIR filter order and SNR

This error rate decreases when the order of the YuleWalk IIR band pass filter increases. However, the identification performance improves when signal to noise ratio SNR exceeds 10dB. In this case, the average error rate estimation stabilizes gradually to reach an asymptotic value.

Although the standard deviation of the average estimation error is low, thus by increasing the order of the Yule-Walk IIR band pass filter, the accuracy of the method is improved proportionately. By analyzing figure 9, the fault harmonics discrimination having low amplitudes is so difficult because the power average estimation error reaches a maximum value especially when the SNR decreases. Thus a satisfactory recognition results requires an SNR greater than 15dB.

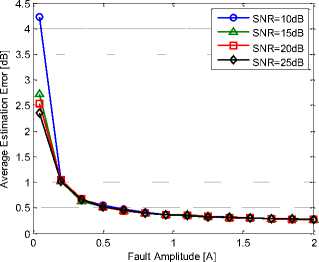
Fig 9. Variation of fault powers estimation error according to fault amplitude and SNR

Against, when the fault magnitude increases the algorithm becomes able to track automatically the harmonics more accurately.

frequency range is wide. It is noted that this computation time is the twice compared to the time required to detect the previous faults.

X= 50

Y= 16.853

X= 89.232

Y= -18.0943

X= 155.2504

Y= -15.6437

-20

40     60     80    100    120    140    160    180

Frequency [Hz]

Fig 11. Power and Frequency estimates by Fast-ESPRIT for bearing damage fault

D. Misalignment detection

In this simulation, Fast-ESPRIT method has been evaluated to identify an important number of harmonics charactering misalignment fault signature in the frequency bandwidth [10, 210]Hz.

X= 49.9997

Y= 16.9624

I0

-5

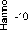
-15

-20

X= 25.8197

Y= -10.8738

X= 22.5109

Y= -14.681

X= 70.8638

Y= -12.3858

X= 74.1743

Y= -11.5157

Table 7. Misalignment fault parameters

f mis (Hz)	I mis (A)	P mis (dB)	N h	SNR (dB)
21	0.22	-16.16
37.03	0.33	-12.64
79	0.27	-14.38	7	20
95.05	0.37	-11.65
137.03	0.18	-17.90
195.05	0.15	-19.49

10     20     30     40     50     60     70     80     90

Frequency [Hz]

Fig 10. Power and Frequency estimates by Fast-ESPRIT for broken rotor bars fault

Referring to the figure 12, the applied method offers good estimation ability with a very good computation cost equal to 0.07178 second.

Figure 10 provides the achieved detection by the proposed method of broken rotor bars fault harmonics. It is noted that the Fast-ESPRIT algorithm was able to separate spectral components much closer and lower accurately in an optimal computation time which equal to 0.03021 second.

• C.    Bearing damage detection

In the third test, the proposed algorithm has been used to detect bearing damage fault signature in the frequency range [40, 200]Hz. The table 6 gives the simulated fault parameters.

20   40   60   80   100  120  140  160  180  200

Frequency [Hz]

Fig 12. Power and Frequency estimates by Fast-ESPRIT for misalignment fault

Table 6. Bearing damage fault parameters

f bng (Hz)	I bng (A)	P bng (dB)	N h	SNR (dB)
89.248 155.248	0.2 0.25	-16.99 -15.05	3	20

Figure 11 shows that the proposed approach provides a satisfactory result with high accuracy with a minimum computation cost which reach 0.07093 second even if the

As illustrated in the figure 13, when the frequency bandwidth [ f l , f h ] characterizing a fault contains an upper bound f h which is increased and approaching or exceeding the value F Nyquist /2= F s /4, the decimation factor Г decreases and thereafter the signal data samples increases. This causes the increase of the signal autocorrelation matrix dimension. Consequently this leads to a large calculation time. On the other side, if f h < F Nyquist /2 the computation time required by the Fast

ESPRIT algorithm becomes minimal and it is almost without a big change despite the increase of the fault harmonics number contained in the stator current signal. This increase influences slightly on the calculation time which can be calculated as follows:

T = A tN s c     _r

Where Δt is the time required to process one data sample.

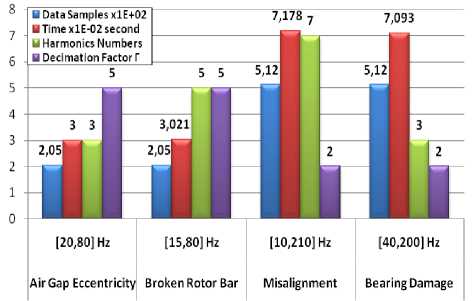
Fig 13. Computation time depending on Fault Frequency range and decimation factor

Another remark that can be added to this interpretation is that the increase of Fs leads to increase the size of the signal data samples. This causes the augmentation of the autocorrelation matrix dimension. As result, the Fast-ESPRIT method takes a long time to discriminate all the frequencies contained in the processed signal with an acceptable accuracy. So in order to adapt accurately the detection algorithm to a real-time application, there is a trade-off between the choice of an optimal sampling frequency in a side and the computation time in the other side.

• VIII. Conclusion

ESPRIT method has better performances than others super resolution algorithms for identifying frequencies from a short data signal acquisition drowned in a noise. However, the main drawback of this technique is the high computational time especially when the size of the signal autocorrelation matrix increases. A new version of the ESPRIT algorithm is proposed in this paper entitled Fast-ESPRIT. An improvement is realized with an adequate IIR band pass filtering and an optimal decimation technique. This enhancement leads to low complexity, to satisfactory accuracy and to memory storage reduction algorithm. The proposed technique was applied under different wind turbine faults to evaluate its resolution ability. Analysis of the simulation results shows that estimator achieves remarkable performance estimation in extracting frequencies and amplitudes in a specified bandwidth than the original ESPRIT. Moreover, due to its advantages, Fast-ESPRIT method can be implementable for real time fault diagnosis. The future work will be focused to ameliorate Fast-ESPRIT detection efficiency in the case of low amplitudes harmonics.