High-Speed and Secure PRNG for Cryptographic Applications
Автор: Zhengbing Hu, Sergiy Gnatyuk, Tetiana Okhrimenko, Sakhybay Tynymbayev, Maksim Iavich
Журнал: International Journal of Computer Network and Information Security @ijcnis
Статья в выпуске: 3 vol.12, 2020 года.
Бесплатный доступ
Due to the fundamentally different approach underlying quantum cryptography (QC), it has not only become competitive, but also has significant advantages over traditional cryptography methods. Such significant advantage as theoretical and informational stability is achieved through the use of unique quantum particles and the inviolability of quantum physics postulates, in addition it does not depend on the intruder computational capabilities. However, even with such impressive reliability results, QC methods have some disadvantages. For instance, such promising trend as quantum secure direct communication – eliminates the problem of key distribution, since it allows to transmit information by open channel without encrypting it. However, in these protocols, each bit is confidential and should not be compromised, therefore, the requirements for protocol stability are increasing and additional security methods are needed. For a whole class of methods to ensure qutrit QC protocols stability, reliable trit generation method is required. In this paper authors have developed and studied trit generation method and software tool TriGen v.2.0 PRNG. Developed PRNG is important for various practical cryptographic applications (for example, trit QC systems, IoT and Blockchain technologies). Future research can be related with developing fully functional version of testing technique and software tool.
Quantum cryptography, information security, pseudorandom numbers (sequences), PRNG, evaluation, trit, quantum deterministic protocol, evaluation, trit, NIST STS
Короткий адрес: https://sciup.org/15017204
IDR: 15017204 | DOI: 10.5815/ijcnis.2020.03.01
Текст научной статьи High-Speed and Secure PRNG for Cryptographic Applications
Published Online June 2020 in MECS DOI: 10.5815/ijcnis.2020.03.01
With the rapid development of information and communication technologies (ICT), most of the world is faced with the problem of supporting cybersecurity (information security). On the one hand, new powerful ICT contribute to the cybersecurity development, and on the other, they create new threats. For the past few years, number of reported cybersecurity incidents of confidential information leaks increases every month.
Today, the reliability and security of traditional cryptographic methods mostly depends on the attacker's computational power and the ability to solve a particular class of mathematical problems in polynomial time. But since the advent of such technologies as GRID computing, supercomputer and quantum computer, which perform complex calculations in minutes – companies, states and scientists have to look for new alternatives to existing security and privacy methods.
There are two major classes of methods to replace traditional cryptography – the first one is quantum cryptography (QC) [1], based on the fundamental difference, the use of the unique capabilities of quantum mechanics; the second is post-quantum cryptography (PQC) [2], based on the more complicated mathematical problems (for example, lattice-based cryptosystems, syndrome-based cryptosystems and others).
Unlike most classical cryptosystems, whose security is based on unproven mathematical assumptions, the security of QC systems relies on fundamental laws of quantum mechanics, which, with proper implementation makes it fundamentally impossible to intercept information and breach its confidentiality. One of the most advanced QC technologies, along with quantum key distribution (QKD), is quantum secure direct communication (QSDC), which allows to transmit information through an open channel directly (without encryption, so the problem of key distribution is eliminated) [3]. Today, a large number of QSDC methods are proposed [4, 6, 8] based on various quantum technologies and can be used both for secure information transmission (using qubits or qudits) and for the cryptographic keys distribution [22, 25]. However, in deterministic QSDC protocols, every bit is confidential and should not be compromised, so the requirements for its stability are much higher than for QKD protocols. The deterministic QSDC protocols disadvantage is that they have only asymptotic resistance (security) to non-coherent attacks and, of course, require security enhancement (amplification) methods.
-
II. Related Works and problem Statement
In [6], the methods of enhancing the QSDC protocols security are described, and the authors proposed and theoretically substantiated method of ensuring QSDC protocols stability. The method developed in [6] requires the generation of ternary (trit) pseudorandom number generator (PRNG) [23], thus increasing the information capacity of transmission protocols. The analysis revealed a sufficient number of existing PRNG that can be used for various applications [4, 5, 7-11, 14, 16].
The ISO/IEC 18031 standard [5], which sets out conceptual models, terminology and requirements relating to the structural elements and properties of systems used to generate random bits in cryptographic applications, defines two types of PRNG: non-deterministic (random bit generation mechanism that uses an entropy source to generate a random bit stream) and deterministic (bit generation mechanism that uses deterministic mechanisms such as cryptographic algorithms on an entropy source to generate a random bit stream).
PRNG can be classified according to different distribution principles [4], but the most complete classification is presented in [7]. According to this classification, PRNG are divided into crypto-resistant and non-crypto-resistant. Crypto-resistant include: based on streaming ciphers (e.g., Dragon-128, SEAL, RC4, RC5, RC6, Grain, Yamb, Phelix), based on block ciphers (for example, GOST 28147-89, AES, ANSI X9.17, DES), based on one-way functions (for example, BBS, RSA, Dual_EC_DRBG (elliptic curves), GPSSD (linear codes), etc.) and non-crypto-resistant: based on elementary recursors (for example, linear congruent, polynomial congruent, additive Fibonacci, additive Fibonacci delayed and multiplicative Fibonacci delayed PRNG), based on operations in finite fields (for example, Genoa generators, Golman, and others) [20, 21, 24, 27].
However, all PRNG developed today are binary sequences oriented, so developing a trit PRNG is an urgent scientific task. In view of this, the authors previously proposed a new method for generating trit PRN in [12]. To verify this method appropriate software needs to be developed. In view of this, the purpose of the article is to carry out detailed experimental study of the proposed trit PRNG for its effectiveness evaluation in various cryptographic applications.
-
III. Theoretical Basis of the Proposed Method and PRNG Construction
The trit generation method includes the following main steps: 1) initialization of the internal state vector; 2) directly PRN generation. Consider shortly each step:
Step 1. Initialization of the internal state vector U is performed. Based on initialization vector VI and secret key K , U e Vn , VI e V „, K e V„ , let’s consider : pen
U = ( x i , x 2 , X 3 , X 4 , X 5 , x 6 , У 1 , y 2 , У 3 , y 4 , k 1 , k 2 , k 3 , k 4 ) , where xi , yj , kj are parts of internal state vector U
( X i e V i , y j e V , k j e V l , i e1,6 , j e 1,4 ); VI = ( VIi, VI 2, VI 3, VI 4, VI 5, VI 6, VI 7, VI8, VI 9, VI10 ) , where VIo are initialization vector parts VI ( VI o e V i , o e 1,10); K = ( K 1? K 2, K 3, K 4 ) , where K w are secret key parts K ( K w e V i , w e 1,4).
Then, the internal vector state U is initialized this way: X i = VI i , y j = VI 6 + j , k j = K j , i e 1,6, j e 1,4.
Step 2. Progressive generation of the output sequence is performed M = (M1,..., Mb ) , M e Vm , Mq are parts of the generated sequence M , Mq e Vn , q e 1, b .
Sub step 2.1. To generate part of the output sequence Mq r -times the following calculations are done:
-
2.1.1. New values of vectors x 1 , x 2 , x 3 ;
-
2.1.2. New values of vectors k 1 , k 2 , y 1 , y 2 ;
-
2.1.3. New vectors x 4 , x 5 , x 6 ;
-
2.1.4. New values of vectors k 3 , k 4 , y 3 , y 4 .
Sub step 2.2 . Using the vector concatenation, the initial sequence is calculated M q : M q = ( y 1 | y 2 1 У з | y 4 ) .
Based on this method TriGen v.2.0 PRNG was developed. Detail algorithm of this PRNG realization is presented on Fig. 1.
TriGen v.2.0
Input: initialization vector VI , secret key K , VI g V24o , K e V96 , parameter b .
Output: output sequence M = ( Mx ,..., Mb ), M e V96b , M q e V 96, q e 1, b .
-
1. x, = VIS, ^ = VI^, k, = Kj,, i e L6 , j E Й .
-
2. For q = Ц ^
-
2.1. For j - 0; j <4; j + + do
-
2.1.1. jq = (S6or(x1+^)©x4) <« k4 ; x2 = (siox(x2+A‘2) + x5)»>^3 j
-
-
-
2.1.2. ^ = Siox^Stiox^ © ^) + x3 J® Vj); ^2 = Sbox^Mix^x^ + £2 + ^6)® J2) ?
-
2.1,3. y. =S6ox(((t + r. I «< v,)©i3);y, = Л&(86ох(((^ +y2)»> ,t3 )©*4))
-
2.1.4. x4 = ^Sbox (x4 + k3 )Ф .iq) «< ^2 i x5 - (-Siox(x3 +k4 )+x2) »> ^ 5
-
2.1.5. k3 =S6ox^(S6ox(x4 ©&3)+x2 )© j)) ; k4= Sbox^Mix^X; +£4 +x3)© y4);
-
2.1.6 r, = Sio.t(((i3 + y3) «< r5 j©^); y4 = Mr(S6or(((t + y4 ) »> х6)ф fc))
-
2.2. M,=(y3|y2|y3|y4)
x3 = Mix ((x3 +x6) Ф у3) «< x3;
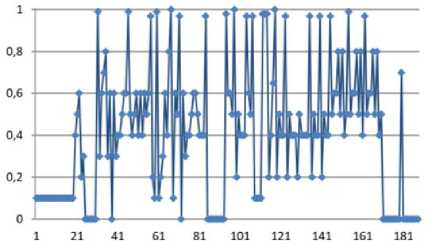
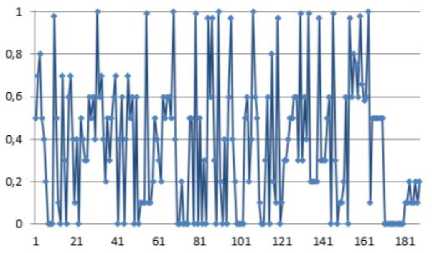
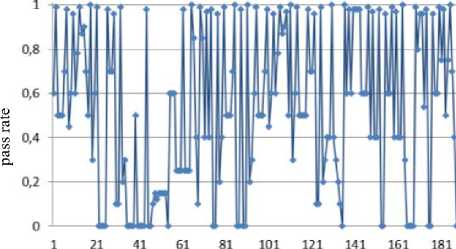
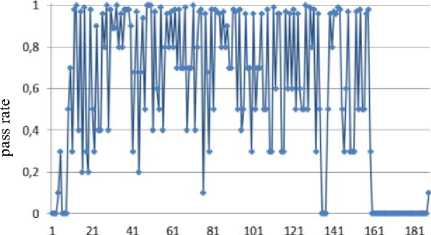
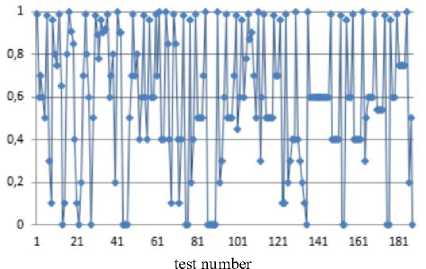
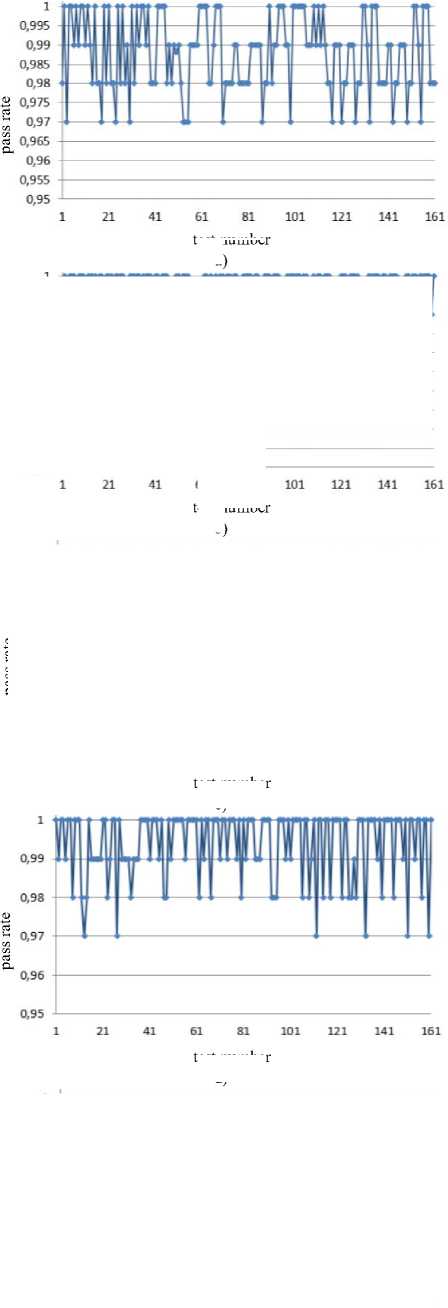
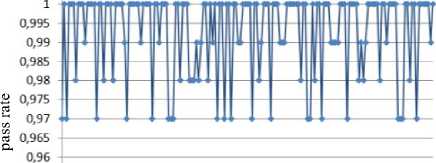
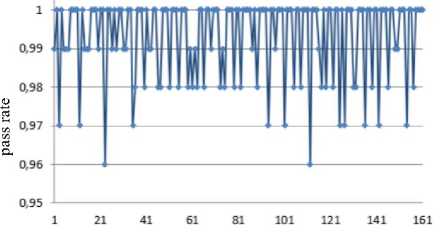
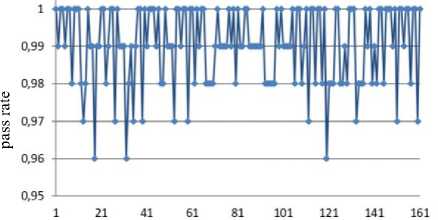
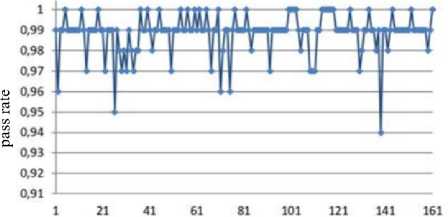
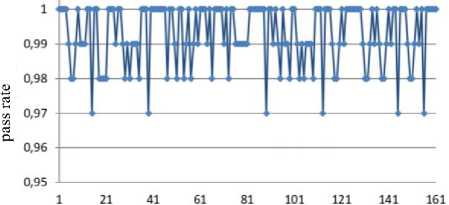
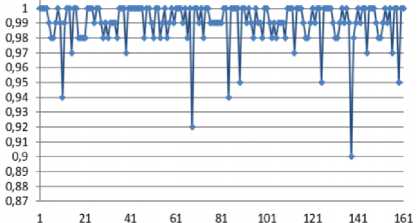
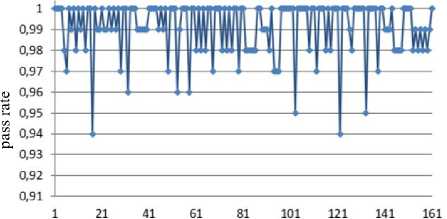
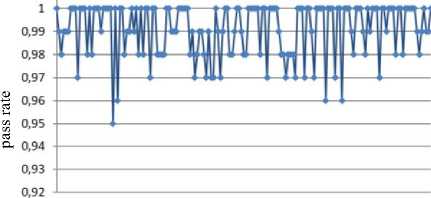
Jt = Mt((J,+i!)ey1)« Fig.1. Pseudocode of TriGen v.2.0 PRNG IV. Experimental Study of the Trit PRNG The purpose of the experiments is to investigate the effectiveness of the developed PRNG in comparison with the known C ++ PRNG and tested its adequacy. To achieve the experimental target, the following tasks are required: 1. To test proposed and known method of generating trit PRN using the NIST STS method. 2. To test proposed and known method of generating trit PRN using the method of evaluating the trit PRN quality described previously by authors in [13]. The input parameters: generated by the TriGen v.2.0 PRNG sequences (PRN are transformed from ternary to binary) and sequences generated by standard C ++ PRNG. Output parameters: NIST STS passing results and TriGen v.2.0 PRNG quality assessment developed using proposed console application. Procedure for the experiments: 1. Generate 100 sequences by PRNG (TriGen v.2.0 PRNG and standard C ++ PRNG), convert trits to bits, and then check them by NIST STS software for pseudorandomness. 2. Generate 100 sequences by PRNG (TriGen v.2.0 PRNG and standard C ++ PRNG), and then test them for pseudo-randomness using the developed TriGen v.2.0 PRNG console application. A. Testing PRN by the NIST STS method Initially, the proposed method of trit PRN generating was decided to test by the NIST STS method [18] in order to check whether standard bit tests can adequately assess trit PRN. NIST STS are used to determine the qualitative and quantitative features of the sequences randomness. Three basic criteria are used to draw conclusions about passing random sequences of statistical tests [17-19] are following: 1. Criterion for decision-making based on the establishment of some threshold level. 2. Criterion based on establishing a fixed confidence interval. 3. Criterion for some appropriate statistical test probability value P-value. The statistical test is based on the verification of null hypothesis H0 – that the sequence under study is random [15, 18, 19]. Alternative hypothesis H1 is also provided – the sequence under study is not random. Therefore, the generated sequence is examined by a set of tests, each of which concludes whether the hypothesis H0 is rejected or accepted. For each test, adequate randomness statistics are selected based on which the hypothesis H0 is further rejected or accepted. Theoretically, the distribution of statistics for the null hypothesis is calculated using mathematical methods. The critical value is then determined from such an exemplary distribution. When performing the test, the value of the test statistic is calculated, which is compared to the critical value. In case of exceeding the test critical value over the reference, hypothesis H1 is accepted, otherwise - hypothesis H0. For the experiments, the following input parameters were selected for the use of NIST STS (according to [18, 19]): 1. The length of the test sequence n=106bit. 2. The number of sequences being tested m=100. 3. Significance level a = 0,01. 4. Number of tests q=188, among them: Frequency - 1, Block Frequency - 1, Cumulative Sums - 2, Runs - 1, Longest Run - 1, Rank - 1, FFT - 1, Non Overlapping Template - 148, Overlapping Template - 1, Universal -1, Approximate Entropy - 1, Random Excursions - 8, Random Excursions Variant - 18, Serial - 2, Linear Complexity - 1. According to [13] a confidence interval rule was applied, the lower bound being 0.96015. For experiments, a console software called TriGen v.2.0 was developed in C ++ programming language, which allows to generate trit sequences based on proposed algorithm TriGen v.2.0 and the standard C ++ PRNG. The experiments were decided to conduct in accordance to standard approach [18] as follows: 1. Each generator under study (TriGen v.2.0 algorithm and standard C ++ PRNG) generated three sequences of 6×107trit. 2. There was a transformation of the trit sequence into a binary number system. To do this, the trit sequence was divided into 24 trit blocks, each block being individually transformed into 40 bit sequences. The result is a binary sequence of 108bits in length. 3. The binary sequence was checked by NIST STS. As a result, statistical portraits of the sequences were obtained. Generation of trit PRN with standard C ++ PRNG was performed as shown on Fig. 2. Input: vectors k and a , k e V32, a e V32 ( V = {0,1}n). Output: output sequence M =( M,,..., M„), Mq e{0,1,2} n, q e1,n . 1. x = к, у = a; 2. std .srand^std ::Z/me(0)J; 2. For q = l;q 2.1. For у = 0; у <4; j++do 2.1.1. 6 = (randQ+x) Ф у; 2.1.2. c = (rand()+у)фх; 2.1.3. y = (rand() +b)®c 2.1.4. x = (rand() +у)ФЬ 2.2. Af[q] = x%3; Fig.2. Pseudocode for trit sequences generating procedure by standard C ++ PRNG The trit PRN generation by the proposed algorithm TriGen v.2.0 was performed as described above. For each sequence, the initial values of the 24 trit vectors ki,, i e 1,4 were set separately, after which the sequences were generated. Firstly, describe the study results for C++ PRNG. Table 1. Inputs for C ++ PRNG for further NIST STS testing C++ gen Initial parameters Sequence 1 k = 314342312 a = 403242341 Sequence 2 k = 3834425654 a = 234525320 Sequence 3 k = 2577261391 a = 980904215 The results of the NIST STS tests, for the trit sequences generated by C ++ PRNG and transformed into binary form for further testing, are presented in Fig. 3-5. Fig.3. Statistical portrait of C ++ gen sequence 1 In the first case, the sequence was tested with only 3 test above the 99% threshold and 6 test with the 96% threshold. Conclusion: The generated sequence failed tests. test number Fig.4. Statistical portrait of C ++ gen sequence 2 The results of the second experiment: 99% – passed 7 tests, the threshold 96% – 22. Which indicates that the generated sequence also failed testing. test number Fig.5. Statistical portrait of C ++ gen sequence 3 test number Fig.7. Statistical portrait of TriGen v.2.0 sequence 2 (NIST STS) The third result indicates that the threshold of 99% passed – 10 tests, and the threshold of 96% passed – 18. Which means that the generated sequence also failed testing. Let’s describe results of the TriGen v.2.0 algorithm study. Sequence 2 results: the number of tests that have passed the threshold of 99% is 26, the threshold of 96% has passed – 32. The generated sequence by the algorithm TriGen v.2.0 also failed testing. Table 2. Inputs for TriGen v.2.0 algorithm for further NIST STS testing C++ gen Initial parameters Sequence 1 k1 = 000000 000000 000000 000000, k2 = 000000 000000 000000 000001, k3 = 000000 000000 000200 000000, k4 = 000000100000 000000 000000. Sequence 2 k1 = 000001000000 000001011000, k2 = 120000 000000 000210 201001, k3 = 200100 200100 010200100001, k4 = 201010111111 211000 002222. Sequence 3 k1 =102210 210120 001022 010110, k2 = 201001020210121210121011, k3 = 102021022011 120101 122102, k4 = 120220110200102112 011012. test number Fig.8. Statistical portrait of TriGen v.2.0 sequence 3 (NIST STS) In Fig. 6-8 depicts statistical portraits generated by TriGen v.2.0 trit sequences during passing NIST STS tests. Fig.6. Statistical portrait of TriGen v.2.0 sequence 1 (NIST STS) Sequence 1 results: the number of tests that have passed the threshold of 99% is 32, and the threshold of 96% has passed – 41, which indicates that the generated sequence by the algorithm TriGen v.2.0 also failed NIST STS testing. Sequence 3 results: the number of tests that have passed the threshold of 99% – 12, 96% passed – 48. Thus, this generated sequence by the algorithm TriGen v.2.0 also did not pass the testing. Therefore, it can be concluded that standard bit tests cannot correctly evaluate the pseudorandom trit sequences. This can be explained by transformation sequence from trits into bits. With this transformation, the trit block (in this case 24 trits) cannot cover the fully formed bit block (in this case, 40 bits). As far as, 324= 282429536481, and 240 = 1099511627776, thus, the 817082091295 bit block value will never appear in it, so the sequence is predictable. B. Testing PRN by proposed Trit STS method Let’s describe the input parameters for Trit STS application (the parameters are chosen similar to the NIST STS tests): 1. The length of trit sequence n= 150 000 trit. 2. The number of sequences being tested m=100. 3. Significance level a = 0,01. 4. Number of tests q=152, among them: Frequency monotrit test – 1, Frequency block trit test – 1, Trit runs test – 1, Test for the longest run in a block – 1, Trit nonoverlapping template matching test – 148, Trit overlapping template matching test – 1. Thus, the sample size under test was N = 1.5 x1Q7 trit, the number of tests (q) for different lengths q = 152, so the statistical portrait of the generator contains 152 probability P-values. As for the NIST STS tests, we will apply the rule of confidence intervals, i.e. the pass rate of each test should be 0.96015%. TritSTS 2020 (on C ++ language) console software was developed based on the proposed PRN quality assessment method and the above input parameters, which allows to evaluate the quality of Trit PRN and their suitability for use in cryptography. This tool was used in the experiments. The experiments were carried out as follows: 1. Each PRNG under study (TriGen v.2.0 algorithm and standard C ++ PRNG) generated five sequences of length N = 1,5 x1Q7 trit. 2. The resulting trit PRN was checked by the program TritSTS 2020. As a result, statistical portraits of the sequences were obtained. Generation of trite sequences with the standard C ++ PRNG and the proposed TriGen v.2.0 algorithm is described above. Let’s start pseudorandom testing from the results of the TriGen v.2.0 algorithm study. Table 3. Inputs for TriGen v.2.0 algorithm for further TritSTS 2020 testing C++ gen Initial parameters Sequence 1 k1 = 102210 210120 001022 010110, k2 = 201001020210121210121011, k3 = 102021022011 120101 122102, k4 = 120220110200102112 011012. Sequence 2 k1 = 000000 000000 000000 000000, k2 = 000000 000000 000000 000001, k3 = 000000 000000 000200 000000, k4 = 000000100000 000000 000000. Sequence 3 k1 = 000000 000200 000000 001000, k2 = 000200 000010 000000 000001, k3 = 010000 000000 000200 000000, k4 = 000000100000 000000 000000. Sequence 4 k1 = 100020102000100022 011102, k2 = 221100 010101020202 212121, k3 = 111002 020100 210200110202, k4 = 120022102021022001100202. Sequence 5 k1 = 221020102001100022 010112, k2 = 021222110201120001 202021, k3 = 121110 022001112202 210201, k4 = 102212 001021122011 201202. In Fig. 9 depicts statistical portraits of TritSTS 2020 passage. test number a) test number b) 61 81 test number c) test number d) test number e) Fig.9. Statistical portraits of TriGen v.2.0 using TritSTS 2020: sequence 1 (a), sequence 2 (b), sequence 3 (c), sequence 4 (d) and sequence 5 (e) Sequence 1 by TriGen v.2.0 results (Fig.9a): number of tests that passed the 99% threshold – 134, 96% passed – 151. Pvalue ≥0,01 quantity – 150, Pvalue ≥0,01 – 150, P ≥ 0,01 – 151. These results indicate that the generated PRN has passed tests successfully. Sequence 2 by TriGen v.2.0 results (Fig.9b): number of tests that passed the 99% threshold – 123, 96% passed – 153. Pvalue ≥0,01 quantity – 152, Pvalue ≥0,01 – 151, P ≥ 0,01 – 151. These results indicate that the generated PRN has passed tests successfully. Sequence 3 by TriGen v.2.0 results (Fig.9c): number of tests that passed the 99% threshold – 118, 96% passed – 153. Pvalue ≥0,01 quantity – 152, Pvalue ≥0,01 – 151, P ≥ 0,01 – 153. PRN has passed tests successfully. Sequence 4 by TriGen v.2.0 results (Fig.9d): number of tests that passed the 99% threshold – 120, 96% passed – 151. Pvalue ≥0,01 quantity – 142, Pvalue ≥0,01 – 150, P ≥ 0,01 – 153. These results also indicate that the generated PRN has passed tests successfully. Sequence 5 by TriGen v.2.0 results (Fig.9e): number of tests that passed the 99% threshold – 114, 96% passed – 150. Pvalue ≥0,01 quantity – 151, Pvalue ≥0,01 – 150, P ≥ 0,01 – 149. These results indicate that the generated PRN has not passed tests. Let's describe the results for the standard C ++ PRNG tested by TritSTS 2020. test number b) test number c) test number Table 4. Inputs for C ++ PRNG for further TritSTS 2020 testing C++ gen Initial parameters Sequence 1 k = 314342312 a = 403242341 Sequence 2 k = 3834425654 a = 234525320 Sequence 3 k = 2577261391 a = 980904215 Sequence 4 k = 5674312 a = 8476892 Sequence 5 k = 7890212 a = 34095422 Fig. 10 shows statistical portraits for 5 different sequences using TritSTS 2020. test number a) d) 1 21 41 61 SI 101 121 141 161 test number e) Fig.10. Statistical portrait of C++ PRNG using TritSTS 2020: sequence 1 (a), sequence 2 (b), sequence 3 (c), sequence 4 (d), sequence 5 (e) Sequence 1 by C++ PRNG results (Fig.10a): number of tests that passed the 99% threshold – 110, 96% passed – 147. Pvalue ≥0,01quantity – 140, Pvalue ≥0,01 – 143, P ≥ 0,01 – 141. These results indicate that the generated PRN is not bad, but it did not pass the tests. Sequence 2 by C++ PRNG results (Fig.10b): number of tests that passed the 99% threshold – 108, 96% passed – 151. Pvalue ≥0,01quantity – 144, Pvalue ≥0,01 – 140, P ≥ 0,01 – 145. These results indicate that the generated PRN is not bad, but it did not pass the tests. Sequence 3 by C++ PRNG results (Fig.10c): number of tests that passed the 99% threshold – 121, 96% passed – 152. Pvalue ≥0,01quantity – 150, Pvalue ≥0,01 – 151, P ≥ 0,01 – 152. These results indicate that the generated PRN has passed tests successfully. Sequence 4 by C++ PRNG results (Fig.10d): number of tests that passed the 99% threshold – 110, 96% passed – 147. Pvalue ≥0,01quantity – 140, Pvalue ≥0,01 – 143, P ≥ 0,01 – 141. These results indicate that the generated PRN is not bad, but it did not pass the tests. Sequence 5 by C++ PRNG results (Fig.10e): number of tests that passed the 99% threshold – 116, 96% passed – 149. Pvalue ≥0,01quantity – 137, Pvalue ≥0,01 – 142, P ≥ 0,01 – 141. These results indicate that the generated PRN is not bad, but it did not pass the tests. For clarity, the experimental results are summarized in a Table 5. According to the obtained results, the sequences generated by the proposed algorithm TriGen v.2.0 showed better results than standard C ++ PRNG. Table 5. Test results for TritSTS 2020 Sequence р , value01 р , value02 р , value12 Number of successful passing tests 99% 96% TritGen 1 150 150 151 134 151 TritGen 2 133 151 153 123 150 TritGen 3 152 151 153 118 153 TritGen 4 142 150 153 120 151 TritGen 5 151 150 149 114 150 C++ PRNG 1 140 143 141 110 147 C++ PRNG 2 144 140 145 108 151 C++ PRNG 3 150 151 152 121 152 C++ PRNG 4 138 133 129 109 145 C++ PRNG 5 137 142 141 116 149 TritGen average 145,6 150,4 151,8 121,8 151 C++PRNG average 141,8 141,8 141,6 112,8 148,8 Note that from five sequences generated by the standard C ++ PRNG, only one passed tests by TritSTS 2020, and four of the five sequences successfully passed tests using the TriGen v.2.0 PRNG. In average, the sequences generated by the TriGen v.2.0 algorithm are 11.6% more likely to successfully pass 99% threshold and 3.4% more likely to successfully pass 96% threshold. V. Conclusions In this paper high-speed and secure PRN generation method was proposed. It is important for various practical cryptographic applications (for example, trit QC systems, IoT and Blockchain technologies). This method includes the following steps: initialization of the internal state vector and directly PRN generation. Based on this method TriGen v.2.0 PRNG was developed and studied in practice. Therefore, analyzing the results of the study it can be conclude that NIST STS technique cannot be used to evaluate the quality of the trit sequences (this technique is oriented on bit sequences evaluation), and the developed method as well as PRNG based on it for evaluating trit sequences quality [26, 28] suitable for use in practice. Future research study can be related with developing fully functional version of TritSTS 2020 technique and software tool. Acknowledgment This scientific work was partially supported by RAMECS and self-determined research funds of CCNU from the colleges’ primary research and operation of MOE (CCNU19TS022) as well as Young Scientists Research Project of the Ministry of Education and Science of Ukraine.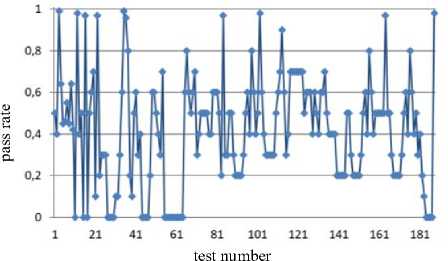

Список литературы High-Speed and Secure PRNG for Cryptographic Applications
- Korchenko O., Vasiliu Y., Gnatyuk S. Modern quantum technologies of information security against cyber-terrorist attacks, Aviation, Vol. 14, №3, рр. 58-69, 2010.
- A. Kuznetsov, I. Svatovskij, N. Kiyan and A. Pushkar'ov, Code-based public-key cryptosystems for the post-quantum period, 4th International Scientific-Practical Conference Problems of Infocommunications. Science and Technology (PIC S&T), Kharkiv, 2017, pp. 125-130. DOI: 10.1109/INFOCOMMST.2017.8246365
- S. Gnatyuk, T. Zhmurko, P. Falat, Efficiency Increasing Method for Quantum Secure Direct Communication Protocols, Proceedings of the 2015 IEEE 8th International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS’2015), Warsaw, Poland, September 24-26, Vol. 1, 2015, рр. 468-472.
- Gnatyuk S., Akhmetov B., Kozlovskyi V., Kinzeryavyy V., Aleksander M., Prysiazhnyi D. New Secure Block Cipher for Critical Applications: Design, Implementation, Speed and Security Analysis, Advances in Intelligent Systems and Computing, Vol. 1126, pp. 93-104, 2020.
- Gorbenko I., Shapochka N., Kozulin O., Requirements statement for random bit generators in accordance to ISO/IEC 18031, Radioelectronics and Computer Systems, 2009, №6 (40), pp. 94-97 (in Ukrainian).
- Z. Hu, S. Gnatyuk, T. Okhrimenko, V. Kinzeryavyy, M. Iavich, Kh. Yubuzova, High-Speed Privaсy Amplification Method for Deterministic Quantum Cryptography Protocols Using Pairs of Entangled Qutrits, CEUR Workshop Proceedings, Vol. 2393, pp. 810-821, 2019.
- Yevseev S., Korolyov R., Krasnyanska M., Analysis of up-to-date methods for pseudorandom numbers generation, Eastern-European Journal of Enterprise Technologies, 2010, Vol. 3/4 (45), pp. С. 11-15. (in Ukrainian).
- Gnatyuk S., Kinzeryavyy V., Kyrychenko K., Yubuzova Kh., Aleksander M., Odarchenko R. Secure Hash Function Constructing for Future Communication Systems and Networks, Advances in Intelligent Systems and Computing, Vol. 902, pp. 561-569, 2020.
- Kalugin A. Modification of multilevel pseudorandom sequences by binary LFSR-CNS generators, Computer optics, 2005, № 28, pp. 112-118 (in Russian).
- Korolyov R. Periodical characteristics study of pseudo-random number generators based on abnormal block codes using, Systems of weaponization and military technics, 2008, № 3 (15), pp. 126-128 (in Ukrainian).
- Mohammed Abdul Samad AL-Khatib, Auqib Hamid Lone, Acoustic Lightweight Pseudo Random Number Generator based on Cryptographically Secure LFSR, International Journal of Computer Network and Information Security (IJCNIS), Vol.10, №2, pp. 38-45, 2018.
- Qoussini A.E., Daradkeh Y.I. Al Tabib S.M., Gnatyuk S., Okhrimenko T., Kinzeryavyy V. Improved model of quantum deterministic protocol implementation in channel with noise, Proceedings of the 2019 10th IEEE Int. Conf. on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS 2019), 2019, pp. 572-578.
- Gnatyuk S., Zhmurko T., Kinzeryavyy V., Seilova N., Method for evaluating trit pseudorandom sequences quality for cryptographic applications, Information Technology and Security, 2015, Vol. 3, №2 (5), pp. 108-116 (in Ukrainian).
- Nazarov Ye., Gubenko N., Pseudorandom generators for cryptographic systems, Scientific works collection of Int., scien.-tech. conf. “Informatics and computer technologies - 2012”, DonNTU, 2012, pp. 139-144 (in Ukrainian).
- Potiy O., Orlova S., Grinenko T. Statistical testing PRNG using statistical tests NIST STS, Regulatory, normative and metrological providing of information security systems in Ukraine, 2001, issue 2, pp. 206-214 (in Ukrainian).
- Rysovanyy O., Gogotov V., Generator of pseudorandom sequences by modulo 3 with various frequencies of pseudo random numbers generating, Information processing systems, 2010, Vol. 2 (83), pp. 141-143 (in Ukrainian).
- A Statistical Test Suite for the Validation of Random Number Generators and Pseudo Random Number Generators for Cryptographic Applications. NIST Special Publication 800-22, May 15, 2001, 164 р.
- NIST STS, Download documentation and software https://github.com/kravietz/nist-sts
- M. Sys, Z. Riha, V. Matyas, K. Marton, A. Suciu, On the Interpretation of Results from the NIST Statistical Test Suite, Romanian Journal of Information Science and Technology, Vol. 18, № 1, 2015, pp. 18-32.
- I. Gorbenko, O. Kuznetsov, Y. Gorbenko, A. Alekseychuk and V. Tymchenko, Strumok key stream generator, IEEE 9th International Conference on Dependable Systems, Services and Technologies (DESSERT), Kyiv, Ukraine, 2018, pp. 294-299.
- S.K. Pal, S. De, An Encryption Technique based upon Encoded Multiplier with Controlled Generation of Random Numbers, International Journal of Computer Network and Information Security (IJCNIS), Vol.7, Issue 10, pp. 50-57, 2015.
- S. Gnatyuk, T. Okhrimenko, M. Iavich, R. Berdibayev, Intruder Control Mode Simulation of Deterministic Quantum Cryptography Protocol for Depolarized Quantum Channel, Proceedings of 2019 Intern. Scientific-Practical Conf. on the Problems of Infocommunications. Science and Technology (PIC S&T 2019), Kyiv, Ukraine, October 08-11, 2019, рр. 825-828.
- Md. A. Ali, E. Ali, Md. A. Habib et al, Pseudo Random Ternary Sequence and its Autocorrelation Property Over Finite Field, International Journal of Computer Network and Information Security (IJCNIS), Vol. 9, Issue 9, pp. 54-63, 2017.
- L. Poluboyina, S. Reddy, M. Prasad, Evaluation of QoS Support of AODV and its Multicast Extension for Multimedia over MANETs, International Journal of Computer Network and Information Security (IJCNIS), Vol.12, Issue 1, pp. 13-19, 2020.
- O. Baranovsky, O. Gorbadey, A. Zenevich et al, Quantum method of secure key distribution in optical fiber communication lines, Proceedings of Intern. Conf. on Information and Telecommunication Technologies and Radio Electronics, UkrMiCo 2017, Odessa, 2017, 8095366.
- A. Prokofev, A. Chirkin, G. Ivanov, Issues of Quality Assessing of Stochastic Transformations Results, Conf. of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus) 2020 IEEE, pp. 463-467, 2020.
- I. Gorbenko, A. Kuznetsov, Y. Gorbenko, A. Pushkar’ov, Y. Kotukh and K. Kuznetsova, Random S-Boxes Generation Methods for Symmetric Cryptography, IEEE 2nd Ukraine Conference on Electrical and Computer Engineering (UKRCON), Lviv, Ukraine, 2019, pp. 947-950.
- A. Kuznetsov, O. Nariezhnii, I. Stelnyk, T. Kokhanovska, O. Smirnov and T. Kuznetsova, Side Channel Attack on a Quantum Random Number Generator, 2019 10th IEEE Intern. Conf. on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Metz, France, 2019, pp. 713-717.


