Histogram Equalization-A Simple but Efficient Technique for Image Enhancement
Автор: Saurabh Chaudhury, Ananta Kumar Roy
Журнал: International Journal of Image, Graphics and Signal Processing(IJIGSP) @ijigsp
Статья в выпуске: 10 vol.5, 2013 года.
Бесплатный доступ
This paper demonstrates the significance of histogram processing of an image particularly the histogram equalization (HE). It is one of the widely used image enhancement technique. It has become a popular technique for contrast enhancement because the method is simple and effective. The basic idea of HE is to re-map the gray levels of an image. Here we propose two different techniques of Histogram Equalization namely, the global HE and local HE. The Histogram Equalization has been performed in the MATLAB environment. The merits and demerits of both techniques of Histogram Equalization have also been discussed. It is seen after exhaustive experimentation on a number of sample images that the proposed image enhancement techniques can be considered as an improvement over the inbuilt MATLAB function histeq.
Image processing, Histogram Equalization, Contrast Enhancement, global equalization, local equalization
Короткий адрес: https://sciup.org/15013076
IDR: 15013076
Текст научной статьи Histogram Equalization-A Simple but Efficient Technique for Image Enhancement
Published Online August 2013 in MECS (http://www.
Digital image processing is an important area of research today and it encompasses two major application areas of interest namely, improvement of pictorial information in an image for human interpretation, and processing of scene data for autonomous machine perception. Image enhancement is among the simplest and most appealing areas of digital image processing. Basically, the idea behind enhancement techniques [1] is to bring out detail that is obscured, or simply to highlight certain features of interest in an image. Many times it is needed to process the image in order to remove noises which are inadvertently introduced in the image. It may be caused by the sensor and circuitry of a scanner or digital camera. Image noise can also originate from film grain and from unavoidable shot noise of an ideal photon detector. Image noise is an undesirable by-product of image capturing that adds spurious and extraneous information. High levels of noise are almost always undesirable, but there are cases when a certain amount of noise is useful, for example, to prevent discretized artifacts (color banding or posterization). Even sometimes noise also increases acutance (apparent sharpness). Noise purposely added in an image is called dither, wherein it improves the image perceptually, though it degrades the signal-to-noise ratio.
It is important to keep in mind that enhancement is a very subjective area of image processing. Image enhancement can be carried out in two domains-spatial domain and frequency domain. Histogram and its equalization is a spatial domain or pixel domain processing wherein some manipulation is carried out in the image pixels in order to have enhanced image. In general, a histogram is the estimation of the probability distribution of a particular type of data. An image histogram is a type of histogram which offers a graphical representation of the tonal distribution of the gray values in a digital image. For an 8-bit grayscale image there are 256 different possible intensities, and so the histogram will graphically display 256 numbers showing the distribution of pixels amongst those grayscale values. By viewing the image histogram, we can analyze the frequency of appearance of the different gray levels (intensities) contained in the image. The histogram that shows only a fraction of the total range of gray levels in the image then the image has low contrast. Each color level (gray value) is represented as a point on x-axis and on y-axis is the number instance of a color level repeats in the image. Histogram may be viewed with Matlab imhist command. Sometimes all the important information in an image lies only in a small region of colors, hence it is usually difficult to extract information from that image. There comes the need for histogram equalization. A good histogram is that which covers all the possible values in the gray scale used. This type of histogram suggests that the image has good contrast and that details in the image may be observed more easily.
A. Histogram Equalization (HE)
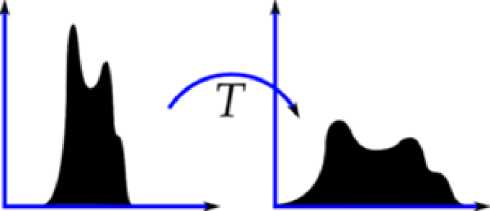
Various enhancement schemes are used for enhancing an image which includes gray scale manipulation with different transformation operators (such as arithmetic and logic operators), filtering and Histogram Equalization (HE) [2,3,4,5,6]. Histogram equalization is one of the well known image enhancement techniques. It became a popular technique for contrast enhancement because this method is simple and effective. In the latter case, preserving the input brightness of the image is required to avoid the generation of non-existing artifacts in the output image. The basic idea of HE method is to re-map the gray levels of an image. HE tends to introduce some annoying artifacts and unnatural enhancement. Fig. 1 shows the image and its histogram and how the transformation by HE results in enhanced image.

Distorted Image Enhanced Image
-
(a) (b)
Figure 1. (a) Original image and its histogram (b) Enhanced image and equalized histogram
B. Adaptive Histogram Equalization
This is an extension to traditional histogram equalization technique. It enhances the contrast of images by transforming the values in the intensity image I. Unlike histeq , it operates on small data regions (tiles), rather than the entire image. Each tile's contrast is enhanced, so that the histogram of the output region approximately matches the specified histogram. The neighboring tiles are then combined using bilinear interpolation in order to eliminate artificially induced boundaries. The contrast, especially in homogeneous areas, can be limited in order to avoid amplifying the noise which might be present in the image.
The degree of discernible details or resolution of an image depends on two main parameters. First, it is the number of samples in each dimension and second, is the number of intensity levels. Larger the number of these parameters closer the digital image approximates the real world image. However, the process of developing measures of image fidelity is subjective and application dependent.
C. Histogram Equalization Techniques
There are a number of different types of histogram equalization algorithms, such as cumulative histogram equalization, normalized cumulative histogram equalization, and localized equalization. A detailed list of histogram equalization techniques and their advantages and disadvantages are explained in [7]. Histogram expansion is a simple technique that enhances the contrast levels of an image. But it has the disadvantage that if there are gray values that are physically far apart from each other in the image then this method fails. LAHE offers an excellent image enhancement technique in terms of contrast level but has the disadvantage that it is computationally very slow and requires a high number of operations per pixel. Par sectioning on the other hand is easy to implement and better suits in hardware level, whereas, odd sectioning offers a good image contrast but has problems with histograms which cover almost the full gray scale.
Image histogram and histogram equalization find applications not only in image enhancement but also in other higher level processing such as in thresholding, adaptive thresholding [7], image segmentation [8] and super-resolution, image quality and image restoration. A histogram based thresholding approach might be to create a histogram of the image pixel intensities and use the valley point as the threshold. The histogram approach assumes that there is some average values for both the background and object pixels, but that the actual pixel values have some variation around these average values. The paper is organized as follows. Section II illustrates the proposed algorithms for the global histogram equalization and local histogram equalization respectively and techniques behind such processing. In section III we present our observation on the results of exhaustive experimentation of the proposed techniques on some sample images and finally section IV concludes the paper.
-
II. PROPOSED ALGORITHMS
The Image Enhancement specifically the contrast enhancement [6] using Histogram Equalization techniques that have been proposed here are- Global Histogram Equalization and Local Histogram Equalization. The algorithms and flowcharts of which are discussed in the following subsections. These are implemented using MATLAB scripting.
A. Global Histogram Equalization
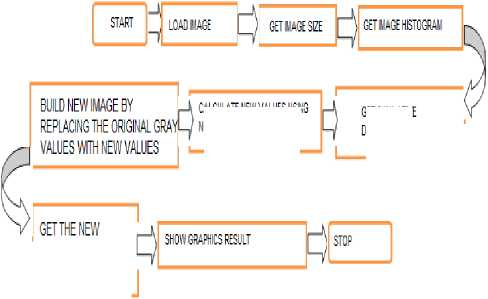
The following flowchart in Fig. 2 depicts the different steps that were followed during the Global Histogram Equalization.
HISTOGRAM AND COMPARE
Figure 2. Flow-chart showing Global Histogram Equalization Technique
Ж« NEW VALUES USING NORMALEEDHISTOGRAM
GETCUMILAI1VE
DISTRIBUTION FUNCTION
Consider a discrete grayscale image{x} and let ni be the number of occurrences of gray level i. The probability of an occurrence of a pixel of level in the image is px(i) = p(x=i) = ni/n, 0≤i L being the total number of gray levels in the image, n being the total number of pixels in the image, and px(i)being in fact the image's histogram for pixel value i, normalized to [0,1]. The cumulative distribution function is defined corresponding to px as cdfx(i)=S^o p(D Where p is a function of x, which is also the image's accumulated normalized histogram. We would like to create a transformation of the form y = T(x) to produce a new image {y}, such that its CDF will be linearized across the value range, i.e. cdfx(i) = iK for some constant K. The properties of the CDF allow us to perform such a transform. It is defined as y= T(x) = cdfx(x) We notice that the T maps the levels into the range [0,1]. In order to map the values back into their original range, the following simple transformation needs to be applied on the result y’= y.{max{x}-min{x}}+ min{x}
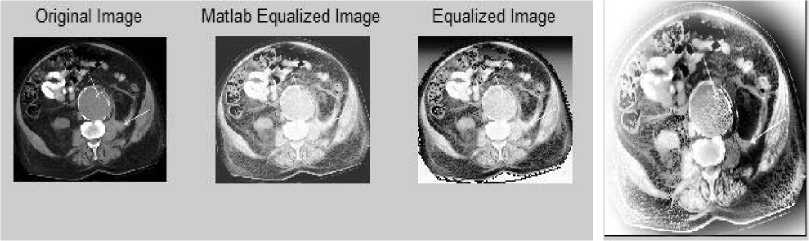
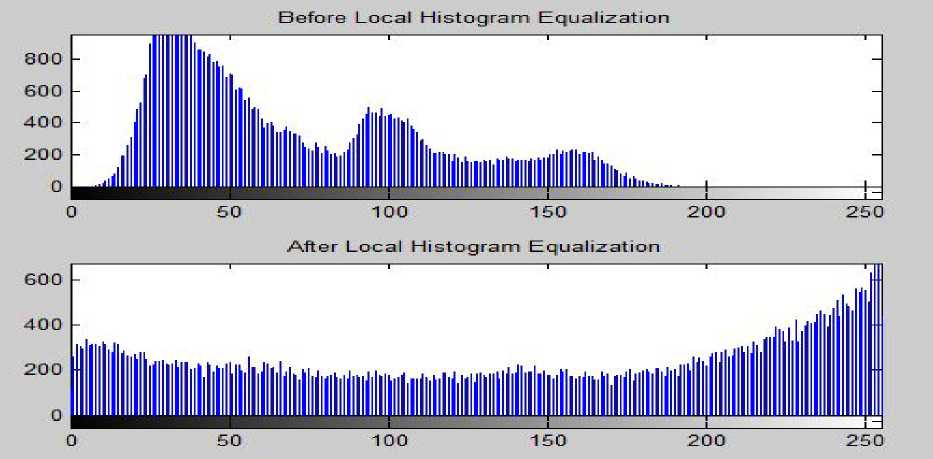
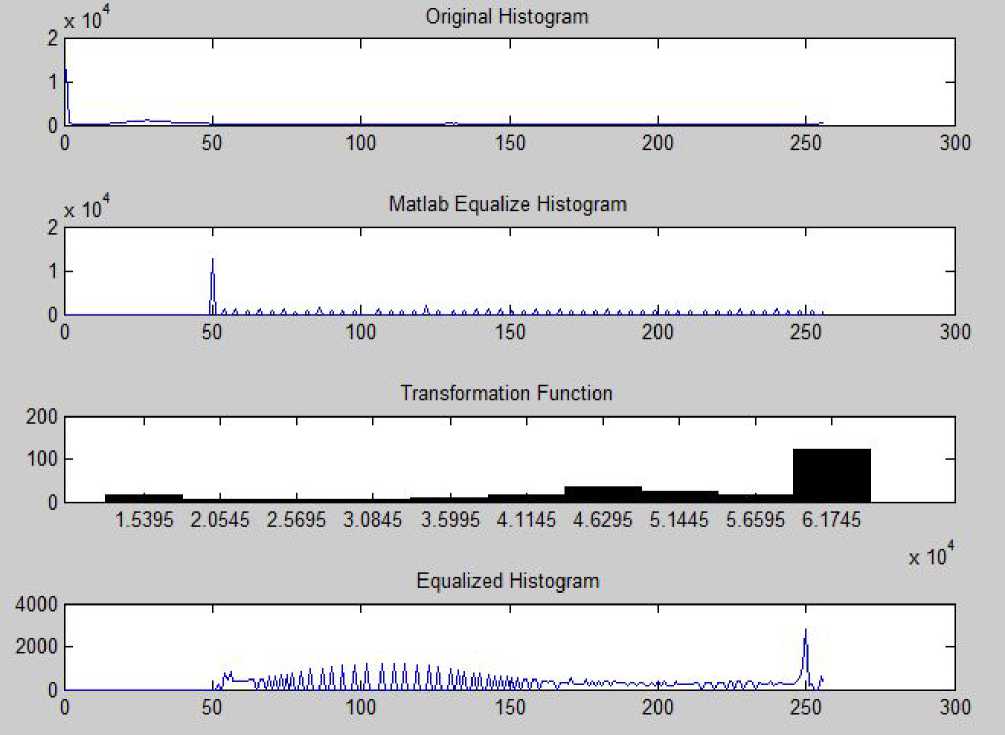
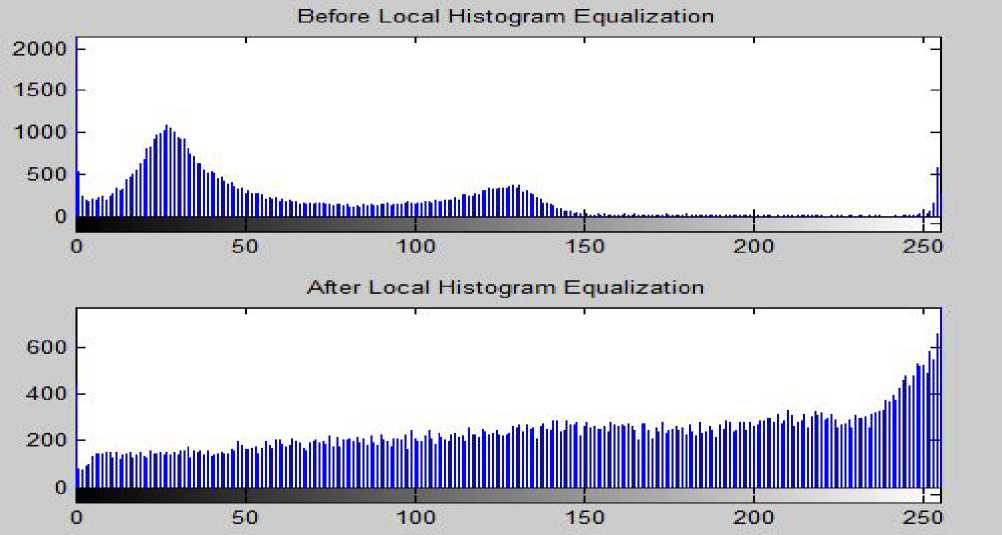
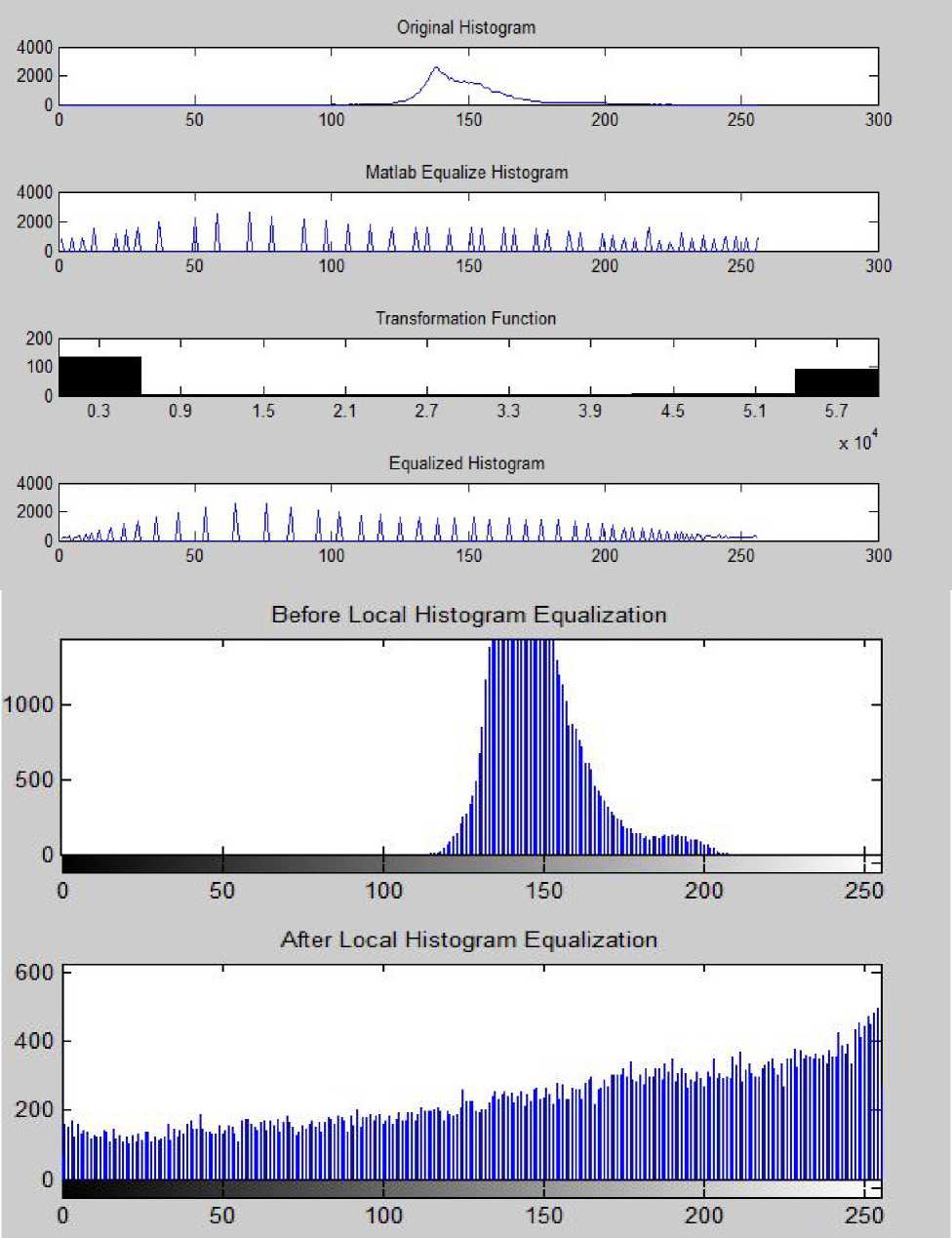
B. Local Histogram Equalization The flowchart as shown Fig. 3 depicts the algorithmic steps that have been implemented in the proposed approach for local histogram equalization and are described as follows. • The input image is loaded and the histogram obtained by using the function imhist [10]. • A window of our own chosen size is initialized. • CDF values for the pixels in the image are computed. • The middle values for each window is computed and the CDF value calculated. • The pixels in the original image are replaced by the new CDF values which depend on the value of the CDF of the middle element. • Img(i,j)=round(cdf(ele)/(M*N)*255) • The histogram of the equalized image is obtained. • Histograms of new and original images are compared. • Print the graphic results. Figure 3. Flow-chart showing the proposed algorithm on local histogram equalization III. OBSERVATIONS AND RESULTS The image of Fig. 5 (a) is a cross section of the human heart showing the aorta (largest artery) by a big grey sphere in the original image and the histogram of it is shown in Fig. 8. Here, we observe that the contrast distribution is not uniform and we cannot categorize the image into a bright foreground and a dark background. The MATLAB equalized image has brighter contrast but the various parts in the cross section cannot be easily distinguished. The proposed algorithms using both global and local equalization clearly show the different contrast regions and most importantly the different parts within the cross section are more clearly visible. In fact the local histogram method scores above the global histogram technique in this particular medical image. It is able to clearly distinguish the different parts within the crosssection irrespective of the details outside the boundaries. The different contrast gradients in the image have been easily expressed. This may help doctors to diagnose whether any problem exists in the artery. Thus the proposed algorithm scores above the MATLAB equalization technique. In case of satellite image of Fig. 6, both the MATLAB equalized image and the global histogram equalized image are better contrast images than the original low contrast image obtained from the satellite. The equalized image (global HE) differs from the MATLAB equalized image in the regions in the lower left of the landscape as it brings out better contrast level than the MATLAB image. On the other hand, locally equalized image exposes much more details than the global histogram equalized image. The image has exposed details like trees and fields in the right half of the image. Also the intensity distribution is higher at the edges as expected and hence the gray levels of the boundary pixels have been overamplified. Fig. 9 shows the image histograms of satellite captured image. Figure 4. (a) image of Monalisa, Images, (b to d) are the images after Matlab, global HE, local HE Figure 5. (a) cross-section of human heart, (b to d) are the images after Matlab, global HE and local HE Figure 6. (a) Satellite captured Image, (b to d) are images after Matlab, global HE and local HE о Matlab Equalize Histogram ----------------------------1-----------------------------1-----------------------------1-----------------------------1-----------------------------1— м!шш Ш1№«м^ О 50 100 150 200 250 Transformation Function 200 --------1-----------------1-----------------1-----------------1-----------------1-----------------1-----------------1-----------------1-----------------1-----------------1-------- 100 - 0 ^-1---1---1-■^„^^^^^^^^^e^^^^^^M 0.3195 0.9585 1.5975 2.2365 2.8755 3.5145 4.1535 4.7925 5.4315 6 0705 x 104 Equalized Histogram 0 50 100 150 200 250 300 Figure 7: Image histograms of Monalisa Figure 8 : Image histograms of cross-sectional view human heart Figure. 9: Image histograms of satellite captured image IV. CONCLUSIONS In this paper we have seen the usefulness of histogram processing of digital images and proposed two algorithms for histogram equalization namely, the global and local HE. We have also observed the effectiveness of the proposed techniques by applying on three different sets of images. It is clear from the results that for simple images with lesser contrast levels and backgrounds, global histogram give better results whereas when the image is complex with different contrast levels and backgrounds the local histogram equalization works well and produces good results. However, it must be kept in mind that when fast computation is required then one must go for global HE, whereas local HE takes more computational time and requires more memory but capable of enhancing the local details and information in an image with multiple contrast levels. ACKNOWLEDGMENT We sincerely thank Mr. Dipankar Mohato, Mr. Pranoy Bardoloi and Miss Ronalin Kakoti for their useful contributions, discussions and comments towards successful completion of the project.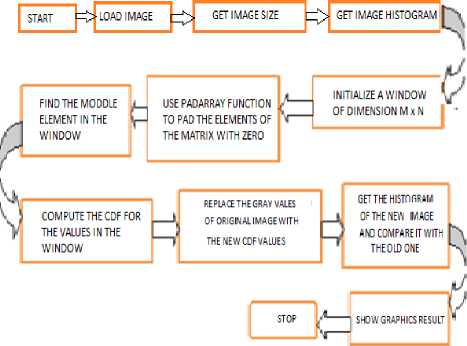



Список литературы Histogram Equalization-A Simple but Efficient Technique for Image Enhancement
- Maini Raman and Agarwal Himanshu: A Comprehensive Review of Image Enhancement Techniques, Journal of Computing, Vol. 2, Issue 3, ISSN 2151-9617, March 2010.
- Garg Rajesh, Mittal Bhawna and Garg Sheetal: Histogram Equalization Techniques For Image Enhancement. H.I.T., Sonepat, Haryana, India.
- Mark Eramian and David Mould: Histogram Equalization using Neighborhood Metrics. Department of Computer Science, 110 Science Place, Saskatoon, SK, Canada, S7N 5C9 ,Canada, S7N 5C9.
- Mokhtar N.R, Harun Nor Hazlyna, Mashor M. Y., Roseline H., Mustafa Nazahah, Adollah R., Adilah H. and Nasir N.F.Mohd: Image Enhancement Techniques Using Local, Global, Bright, Dark and Partial Contrast Stretching For Acute Leukemia Images. In: Proc. of the World Congress on Engineering 2009, Vol I.
- Robert Krutsch and David Tenorio: Histogram Equalization: Technical Report, Microcontroller Solutions Group, Guadalajara.
- Kim Joung-Youn, Kim Lee-Sup and Hwang Seung-Ho: An Advanced Contrast Enhancement Using Partially Overlapped Sub-Block Histogram Equalization, IEEE Trans. on Circuits and Systems for Video Technology, Vol. 11, No. 4, APRIL 2001.
- Freescale Semiconductors : http://cache.freescale.com/files/dsp/doc/app_note/AN4318.pdf
- Rafael C, Gonzalez, Richard E Woods. Digital Image Processing, Pearson Education Inc. 2002, India Reprint. ISBN 81-7808-629-8.
- Shapiro, Linda G. & Stockman, George C. (2002). "Computer Vision". Prentice Hall. ISBN 0-13-030796-3.
- Sabih D. Khan. Image Processing in Matlab: An Introductory Approach.


