History and application of the matrix

The term “matrix” has many meanings. For example, in mathematics, a matrix is a system of elements that has the form of a rectangular table, in programming a matrix is a two-dimensional array, in electronics it is a set of conductors that can be closed at their intersection points. Poker chips are also directly related to the matrix. Poker chips are made from a high-quality composite material, often with a metal core. In turn, the composite material or composite has a matrix and reinforcing elements included in it (with the exception of layered composites).

The matrix in a photograph is an integrated microcircuit (analog or digital-analog), which consists of photodiodes (photosensitive elements). Thanks to the photosensitive matrix, the projected optical image is converted into an electrical signal of an analog type, and if there is an ADC in the matrix, the conversion occurs into a stream of digital data.

The matrix is the main element of digital cameras, all modern video and television cameras, cameras built into the mobile phone and video surveillance systems.

The basic meaning of the term "matrix" has in mathematics.

Matrix is a mathematical object written in the form of a rectangular table of elements of a ring or field (for example, integers or complex numbers), which is a collection of rows and columns at the intersection of which are its elements. The number of rows and columns of the matrix set the size of the matrix. Although historically considered, for example, triangular matrices, nowadays they speak exclusively of rectangular matrices, since they are the most convenient and common.

For the first time the matrix was mentioned in ancient China, then called the "magic square." The main use of matrices was to solve linear equations. Also, the magic squares were known a little later by the Arab mathematicians, approximately then the principle of the addition of matrices appeared. After the development of the determinant theory in the late 17th century, Gabriel Kramer began developing his theory in the 18th century and published the “Cramer's Rule” in 1751. Approximately in the same period of time a “Gauss method” appeared. The theory of matrices began its existence in the middle of the XIX century in the works of William Hamilton and Arthur Cayley. Fundamental results in the theory of matrices belong to Weierstrass, Jordan, Frobenius. The term "matrix" was introduced by James Sylvester in 1850.

Matrices are widely used in mathematics for compact writing of systems of linear algebraic or differential equations. In this case, the number of rows of the matrix corresponds to the number of equations, and the number of columns to the number of unknowns. As a result, the solution of systems of linear equations is reduced to operations on matrices.

Matrices allow the following algebraic operations:

• •    the addition of matrices having the same size;

• •    multiplication of matrices of suitable size (a matrix with n columns can be

multiplied from the right by a matrix with n lines);

• •    multiplying a matrix by an element of the main ring or field (i.e., a scalar).

A matrix is a set of numbers that form a rectangular table that contains m -rows and n - columns. To designate the matrix, the inscription is used:

alla12a13 ■■■ а1/ ••■ aln ^21^22^23 *•• “2/ •” ^2к amlaffl2am3 —Ящ —Яя»/ , аij, where i is the row number, j is the column number

Next, consider the types of matrices.

Matrices C and D are 3x3 and 2x2. In the case when the number of rows of the matrix equals the number of its columns, the matrix is called square. This means that the matrix C is a square matrix of the third order, and the matrix D is a square matrix of the second order.

/ 69 54 20 I 54 138 -5 С= :: - 5 -4

: D= ^

A matrix that contains only one row or one column is called a vector. In such matrices, you can select a row vector and a column vector. So, the matrix K is a row vector, and the matrix F is a column vector.

K="?-; F='-\

The square matrix, in which there are nonzero elements in the main diagonal, and all the rest - zeros is called a diagonal matrix. The matrix L is a third-order diagonal matrix. If nonzero elements are equal only to ones, then this is the identity matrix, it is always denoted by the letter E. In our case, the matrix E is also a third-order identity matrix.

/ 6 0 0 \    /10 0\

0 5 0 1;    0 10

L=        - E=        .

If all elements of the matrix are zero, then this is the zero matrix. For example, the matrix V is a zero matrix of the third order.

/О о О\ ООО V= ; ; ;  .

If in this matrix to change the rows and columns in some places, then the transposed matrix will be given. For example, the matrix M is given, each line of this matrix will be transferred to the corresponding column of the matrix, which is next in the picture. The second matrix is the transposed matrix of matrix M.

If in this matrix to change the rows and columns in some places, then the transposed matrix will be given. For example, the matrix M is given, each line of this matrix will be transferred to the corresponding column of the matrix, which is next in the picture. The second matrix is the transposed matrix of matrix M.

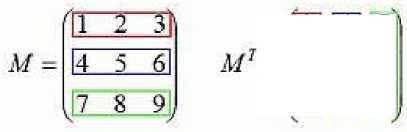
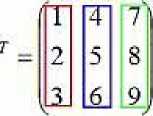
By the middle of the XIX century. matrices have become independent objects of mathematical research. By this time, the rules of matrix addition and multiplication were formulated. The main role in their development was played by the works of Hamilton, Cayley and Sylvester (J.J.Sylvester, 1814–1897). The modern designation of the matrix was proposed by Cayley in 1841. Research Weierstrass (K.Th.W.Weierstrass, 1815–1897) and Frobenius (F.G.L. Frobenius, 1849–1917) far advanced the theory of matrices, enriching it with new content.

But there is also a special kind of matrix, called the magic square. The magic square is a square table of integers in which the sum of the numbers along any line, any column and any of the two main diagonals is the same number.

The magic square is of ancient Chinese origin. According to legend, during the reign of Emperor Yu (c. 2200 BC), a sacred tortoise emerged from the waters of the Yellow River (Yellow River), on the shell of which mysterious hieroglyphs were drawn and these signs are known as los and are equivalent to a magic square. In the 11th century learned about magic squares in India, and then in Japan, where in the 16th century. extensive literature was devoted to magic squares. Europeans introduced magic squares in the 15th century. Byzantine writer E. Moshopoulos. The first square, invented by a European, is A.Durer's square depicted on his famous engraving Melancholy 1. The date of the engraving (1514) is indicated by numbers in the two central cells of the bottom line. Magic mystics attributed various mystical properties. In the 16th century Cornelius Heinrich Agrippa constructed squares of the 3rd, 4th, 5th, 6th, 7th, 8th and 9th orders, which were associated with the astrology of 7 planets. It was believed that the magic square engraved on silver protects against the plague. Even today, among the attributes of European diviners, you can see magic squares.

In the 19th and 20th centuries. interest in magic squares flared up with a new force. They began to explore using methods of higher algebra and operational calculus.

Magic squares of odd order can be constructed using the method of the 17th century French geometer. A. de laLuber. Consider this method on the example of a square of the 5th order. The number 1 is placed in the central cell of the top row. All natural numbers are arranged in a natural order cyclically from bottom to top in the cells of the diagonals from right to left. Having reached the top edge of the square (as in the case of the number 1), we continue to fill in the diagonal, starting from the bottom cell of the next column. Reaching the right edge of the square (number 3), we continue to fill in the diagonal that goes from the left cell to the line above. Having reached the filled cell (number 5) or the angle (number 15), the trajectory goes down one cell, after which the filling process continues.

Where else do matrices apply?

The multiplication table is a product of matrices (1,2,3,4,5,6,7,8,9) T × (1,2,3,4,5,6,7,8,9).

In physics and other applied sciences, matrices are a means of recording data and transforming it. In programming - in writing programs. They are also called arrays. Widely used in technology. For example, any picture on the screen is a two-dimensional matrix, the elements of which are the colors of dots.

In psychology, an understanding of a term is similar to a given term in mathematics, but instead of mathematical objects, certain "psychological objects" are implied - for example, tests.

In addition, the matrix is widely used in economics, biology, chemistry and even in marketing.