Horizontal vertical diagonal Gabor binary pattern descriptor with PLDA for pose-invariant face recognition

Published Online December 2018 in MECS

Reliable face recognition is motivated not only by the essential challenges this classical recognition-problem poses but also by the issues that creep in during its various practical applications where unconstrained face identification is needed. Face recognition is among the core biometric technologies whose applications are growing leaps and bounds due to their significant role in security, surveillance and forensics. Among the conventional steps (face pre-processing, feature extraction, feature matching and feature classification) followed for face recognition, feature extraction is one of the crucial steps. Feature extraction provides information desired for distinguishing between faces of different persons. If the reliable feature set is extracted, then there is increase in the probability of obtaining all relevant information from the input data and henceforth improvement in the recognition rate. However, out of the plethora of face descriptors defined in the literature, only a few can resist the changes in face pose. The primary issue with feature descriptors for pose images is that they not only encode desired subject information but they also encode unwanted pose related information. Whereas, a robust face feature descriptor is expected to retain the subject details intact even though the face has undergone pose transformation like translation, rotation or scaling.

Face descriptors may be categorized based on their application. Descriptors may describe the face appearance holistically or patch-wise, incorporating features of the whole face or a set of features of facial components and thereby comprising dense or sparse descriptors. Descriptors may be data dependent or data independent. Based on learning, learning descriptors may be categorized into shallow learning descriptors or deep learning descriptors. Learning descriptors evolve their characteristics by learning from the training data. Deep learning descriptors often involve a massive volume of the dataset from where the descriptor is to be determined, and deep convolutional networks (CNN’s) are used for the learning process. Though, deep learning descriptors delivers impressive performance but still their processing demands are very high. On the other side, easy to compute face descriptor–intensity based descriptor fails completely when the pose variations are present.

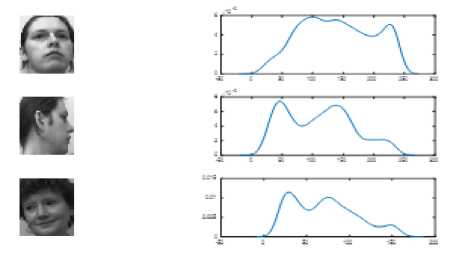
Fig.1. Intensity Descriptor of Same and Different Subject

Their failure may be accounted for considering only appearance information rather than semantic information. During pose change face appearance changes. Fig.1 clearly shows the effect on intensity distribution due to pose change. It can be deduced that intensity distribution undergoes change to such an extent that it may resemble more with the intensity distribution of a different subject rather than its own subject.

Recently, texture based local descriptors have gained attention due to its low computational demands. However, the presence of pose variation restricts one to contemplate a large local neighborhood. In this paper, for the pose invariant feature extraction, non-uniform texture based descriptor: Horizontal Vertical Diagonal Gabor Pattern (HVDGBP) descriptor is proposed by utilizing linear binary pattern and Gabor filters. To reduce the dimensionality of HVDGBP descriptor, Local Linear Embedding (LLE) is utilized. Probabilistic Linear Discriminant Analysis (PLDA) is utilized to boost the discriminative power of dimensionality reduced descriptor. In section two, the related work to LBP based descriptor, Gabor filter based descriptor and PLDA is presented. Section three presents the proposed approach while section four presents the experimental results and analysis of the proposed descriptor. Conclusion and future works are discussed in the Conclusion section.

• II.    Related Works

This section delves into the face descriptors based on Linear Binary Pattern and Gabor filters. A brief review of PLDA is also presented, as it was used to select discriminatory feature set based on the probabilistic framework.

• A.    LBP-Based Face Descriptors

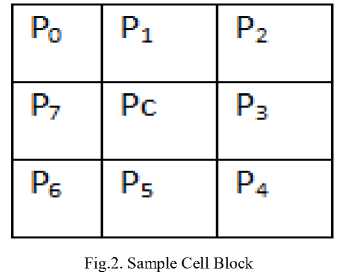
One of the most extensively used local descriptors is the linear binary pattern descriptor proposed by Ojala, Pietikäinen and Harwood [1]. The idea of using LBP is driven by the fact that faces can be seen as a composition of micro-patterns. LBP descriptor describes the local facial texture units by calculating the intensity differences and then encoding the differences of the 3x3 neighborhood. Of 3x3 pixel block, the center pixel of is assigned a value equal to the sum of the encoded values for the differences (eq. 1).

Pc = E s(Pi - Pc).2i where

s ( z )

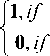
z >= 0

z <  0

Centre pixel encoding of 3x3 blocks, when performed on the whole face image, tend to average over the image area. Spatially enhanced LBP calculates texture descriptors for small face region independently and then calculate the frequency occurrence pattern of encoded differences [2]. The local descriptors are concatenated to form a description of the global geometry of a face image. Spatially enhanced LBP contains information on pixel level, regional level and at complete face image itself. The size of the descriptor is n x m where n is the length of the histogram and m is the number of regions in which face is split into.

• B.    Gabor Descriptors

Gabor descriptors are based on Gabor filters named after Dennis Gabor. Daugman [11] showed correspondence between the 2D Gabor functions and the physiognomies of the mammalian visual system. In the spatial domain, 2D Gabor filter can be represented as Gaussian kernel function modulated by a sinusoidal plane wave, i.e.

G ^ _>v ( z ) = I ( z X_v ( ^z ) (2)

where I(z) denotes the input image and z is the pixel (x, y) which is under consideration and ψ μ,,υ (z) is the Gabor kernel with orientation μ, scale υ and is defined as

^ψ μ,ν

kμ,ν ² σ ²

.e

(

kμ,ν ² .z ²

-    2.2    Ti^^(z) - e - .2/2

kμ,υ is a wave vector and defined as kμ,υ=kυ.eiΦu with Kυ=kmax/fυ (kmax is the maximum frequency, f is the spacing between the kernels in the frequency domain), Φμ is the orientation with value Φμ =(π.μ)/8. Gabor filter gives the peak response at the region where there is a texture change as well at the edge areas. Their response is based on spatial frequency, orientation and direction. Shen, Bai and Fairhurst [12] in their work proved that better recognition accuracy is achieved by using Gabor feature-based methods in place of raw pixels. They also proved that the discriminatory ability of Gabor features is also better as compared to other feature descriptors. Perez, Cament and Castillo [13] proposed Local Matching Gabor (LMG), based on matching the local Gabor features jets by utilizing ‘Borda Count’ strategy. Total computational time for LMG was very high as the total of 4172 Gabor jets were used. Gabor energy feature is utilized by joining the response of the filter to the phase pairs. This resulted in more computational complexity and higher response time. Haghighat, Zonouz and Abdel-Mottaleb [14] in their work proved that a set of Gabor filters with diverse frequencies and orientations is helpful in extracting useful features from an image. Combination of LBP pattern with Gabor filter resulted in extraction the non-uniform LBP Pattern from an input image [20] which can’t be extracted by a uniform LBP Pattern. Recently, Jami, Chalamala, and Kakkirala [15] collectively utilized Gabor wavelet and cross local binary patterns for representing face image features along with the Probabilistic Linear Discriminant Analysis framework for tolerating pose-variations while recognition.

• C.    Probabilistic Linear Discriminant Analysis (PLDA)

LDA is equivalent to maximum likelihood classification under the assumption that each class follows Gaussian distributions. Ioffe [16] proposed “Probabilistic Linear Discriminant Analyzer” (PLDA) that reformulates problem of dimension reduction in a probabilistic context. PLDA model treats the face image as an additive sum of two parts, a deterministic part which depends on an underlying representation of identity only, and a stochastic part which explains the pose variations due to which the two face images from the same person are not identical. LDA is expressed as the maximum likelihood solution of probabilistic latent variables in PLDA, i.e., PLDA uses the latent variable model to define a generative process for each object. The latent variables characterize both the class of the object and the view of the object within the class. Considering training data to be collection of ‘k’ images each of ‘N’ individuals, each pose image (‘j’th) of ‘i’th individual can be modeled as:

x • • = ц + F.h • + G.w • • + £ • • (4) i, j i i, j i, j

The signal part of model (μ+F.hi) is dependent upon the subject identity (there’s no dependence upon j) and poses variation part (G.wij + ϵij,) depends upon the amount of pose variation within subject’s identity. Term μ represents the mean of complete train dataset. The matrix ‘F,’ ‘G’ comprises the basis for a between-individual subspace and within individual subspace respectively. ‘F’ matrix is approximately equivalent to the eigenvectors of the between-individual co-variance matrix and matrix ‘G’ is equivalent to eigenvectors of within individual covariance matrix. ‘F’ variable is shared by all the varied poses of the same subject. The Latent variable ‘hi’ represents the position of the given observation within between-individual subspace (F) and ‘wij’ represent the position of the given observation within individual subspace. The term ‘ϵij’ represents zero mean Gaussian–distributed noise variable with covariance Σ. Hence, the model is parameterized by θ={μ,F,G,Σ}. In the training phase, set of parameters defined by θ are learned from training data ‘wij’. During the recognition phase, the inference is made on the basis of these parameters. PLDA gives a principled method to combine different features in a way that more discriminative features have more impact. In standard PLDA formulation, all latent variables have a Gaussian distribution. The probability distribution of latent variables follows normal distribution i.e.

hi ~N( 0, I )(5)

wij ~ N( 0, I)(6)

~ N( 0, Σ )(7)

The distribution of observed variable can be expressed as:

xij I hi,wij ~ N(xij I v + Fhi + Gwij, £)

Sizov, Lee and Kinnunen [17] provide simple implementation of PLDA via EM algorithm. EM algorithm is utilized for estimation of model parameters. During classification, ‘C’ models (equal to the number of classes) are built up, and the likelihood of the probe data is estimated for these models. Each model represents a relationship between latent identity variable and the latent within individual difference variable .

• III.    Proposed Approach

The proposed approach framework can be divided into four divisions:

• A.    Image Pre-Processing

• B.    Feature Extraction

• C.    Dimensionality Reduction

• D.    Probabilistic Model Building using PLDA.

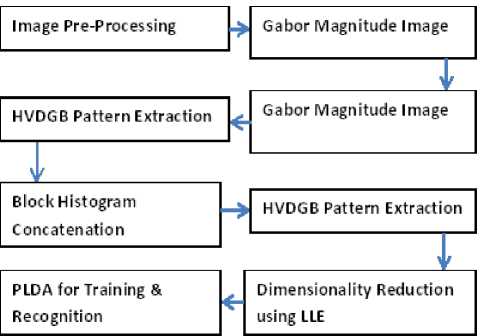
Fig.3. Framework for HVDGBP with PLDA for Face Recognition

• A.    Image Pre-Processing

The Image Pre-processing step consists of face detection. The cropped image undergoes image normalization so that distribution of intensity values of image follows a normal distribution. Gabor magnitude images in the frequency domain are obtained by convolving 40 Gabor filter bank of five spatial frequencies and eight orientation parameters. Magnitude values of each of the 40 images per subject are calculated, and a combined magnitude image is derived. Then a binary pattern is computed using the HVD descriptor of 5x5 non-overlapping cells.

• B.    HVDGBP (Horizontal Vertical Diagonal Gabor Binary Pattern)

The pattern is generated by considering immediate neighbors and extended neighbors of the cell and thresholding function‘s’. Gabor magnitude image is considered as input for HVDGBP. The magnitude image of the complex Gabor filter combines the sensitivity of even and odd parts of the filter into a measure of orientation’s strength. Pattern is generated across 5x5 cell. For each cell ‘C’ represents center pixel, blue colored pixels are the pixels across vertical direction, while red colored pixels are across diagonal directions and green colored pixels are across horizontal direction of the cell. Pattern for the immediate neighboring pixels under consideration, is described by:

D =E 2ⁿ 1s(l - 1 )                  (9)

0 n = 1          .n c where In is the immediate neighbor block under consideration, and Ic is the center pixel of Gabor magnitude image.

For extended neighboring pixels under consideration, the pattern is described by

D 1 =S 2ⁿ 1.s(l 8 + 2,„ — 1 ^- l_c)    (1°)

n = 1

The decimal value for the two binary patterns is then averaged with round off function to convert decimal values to the integer values for assignment to the center pixel.

HVDGP(I c ) =round ((D 0 +D 1 )/2)        (11)

For HVDGBP generation, total sixteen logical comparisons are required for 5x5 cell, and no interpolation of values is required. Since the cell size is 5x5, for an image with dimensions that are not perfect multiples of five, two options can be taken up with one being zero padding and another being leaving the pixels of the fractional block. For this paper, the second option is considered. For an image with 92x112 size, the dimension considered for binary pattern build up is 90x110 with total 18x22=396 non-overlapping cells. For each cell, out of 25 pixels, 16 pixels are considered for the descriptor. Thus, pixel percentage under consideration is reduced by 36% thereby increasing the computation speed. Fig. 4 elaborates the HVDGB pattern generation.

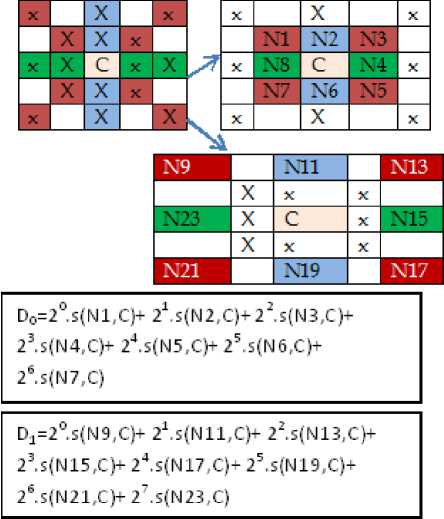
D=(D0+DJ/2

Fig.4. HVD Pattern Extraction from the 5x5 cell.

To extract the local histogram features of HVDGBP image map, concatenated sequence of histograms (H={H 11 , H 12, H 13 H 14 H 15, H 21, H 22 H 23…. H 51 H 52 H 53 H 54 H 55 }) is obtained from all the non-overlapping cells. ‘H’ serve as the facial features. The local histogram extraction process is repeated for all three hundred ninety six cells. The total length of feature vector per image with eight bins per histogram is (90x110)/ (5x5) x 8=3168.

• C.    Dimension Reduction and Classification

  Dimensionality reduction approaches reduces feature vector dimension to improve classification accuracy. Classification accuracy is better if the number of training images is more than the dimensionality of the feature vector. PLDA being a linear model performs best when the data obey linear assumptions. However, face-pose classification is a representative case of non-linear classification, and linear dimension reduction approaches will obviously not be able to give the desired result. LLE (Local Linear Embedding) proposed by Roweis & Saul [18] is used for nonlinear dimension reduction. The internal structure of data is discovered by using the neighbourhood information. The input to LLE consists of feature space of length 3168 of 20 subjects with 10 train images (3168x200) and five neighbourhood points (K=5) per train data point are taken. Optimum dimensionality reduction value is considered after observing the impact on the equal error rate. Then the probability distribution of each class is computed independently. PLDA builds models θ i= {μ i, F i, G i, Σ i } , using latent variables that define inter-class and inter-class variation. Expectation

Maximization algorithm is used to estimate model parameters. During classification, ‘C’ models (equal to the number of classes) are built up, and the likelihood of the probe data is estimated for these models. Each model represents a relationship between latent identity variable and the latent within individual difference variable. Figure 5 represents the constructed models as:

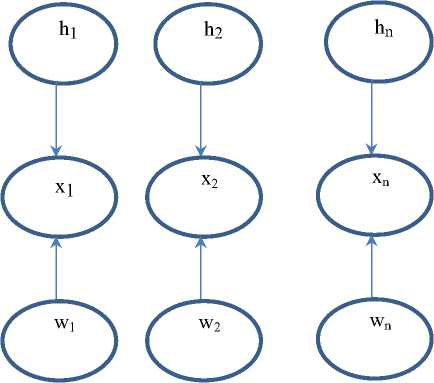
Fig.5. PLDA Model

The log-likelihood ratio is computed for C different models M1,2..C. With the PLDA trained models, the loglikelihood ratio is calculated. From the log-likelihood ratios, the recognition accuracy is calculated between enrolled and probe databases.

Algorithm for Proposed Approach

Procedure HVDGBP_PLDA

Inputs: Train Image Database X ϵ n 1 x R^m , Test Database Yϵ n 2 x Rⁿ partitioned intoEnrollment Database and Probe Database.

Output: Array of Log-likelihood ratios

• a.    Image normalization process is executed for every face image.

• b.    For each image in Train Database (X) & Test Database (Y), compute face features by using HVDGBP descriptor X^' ← HVDBGP(X) , Y^' ← HVDGBP(Y)

• c.    Dimension reduction by utilizing Local Linear Embedding (LLE) with the inputs of the neighbor subset and the value of dimensionality to be retained. U ← LLE(X ^' ),V ← LLE(Y ^' )

• d.    For every class in Train Dataset construct PLDA models. Four parameters of a model is calculated (μ,Σ,F,G):   Mean vector of the

training data, Covariance matrix, Factor loading matrix of latent identity , Factor loading matrix of latent noise variable(pose-variations). To maximize the log-likelihood function in latent variable model, Expectation-Maximization algorithm is utilized.

• e.    Due to the fact that PLDA being a specific form of factor analysis model, different set of parameters will be obtained for different runs. PLDA parameters are taken as average of the specified number of iterations.

• f.    The ‘E- step’ computes the expected values of factor loading matrix corresponding to latent identity variables and latent noise variables.

• g.    In ‘M step’, there is re-estimation of the conditional distribution of latent variables based on the observed data.

• h.    During identification PLDA model parameters are used to calculate log- likelihood between enrolled and probe images by utilizing above mentioned EM steps.

• i.    A low value indicates, as usual, that probe image is different from a enrolled identity.

To extract features from these images, images are processed with Gabor filters (with five scales and eight orientations), and then HVDGP (Gabor pattern) was extracted. Figure 6 shows the instances of Gabor filtered images, and figure 7 shows the Gabor filter bank.

Fig.6. Gabor filtered Image Instances

Fig.7. Gabor Filter Bank

The use of quantized binary codes mitigates small variations introduced due to the expression variation or illumination. Gabor magnitude image is depicted in figure 8(a) while figure 8 (b) and 8(c) are the images obtained by the use of LBP and HVDGBP. From the figures, it can be observed easily that HVDGBP is able to retain all prominent facial features with less noise interference.

Fig.8(a) Gabor Magnitude Image (b) Gabor-LBP Image (c) Gabor-HVDBP Image

After HVDGBP feature extraction step, the dimensionality of the feature vector is reduced further by using Locally Linear Embedding Roweis and Saul [25]. Fig.9 shows the dimensionally reduced images with the neighborhood of five and dimensionality retained at one hundred and ten.

Е Г te> b И F ЫКМНЗИЕЫ sbmii^ir ■hihiiih

• ■ Hill A ■ в

Fig.9. Locally Linear Embedded Images

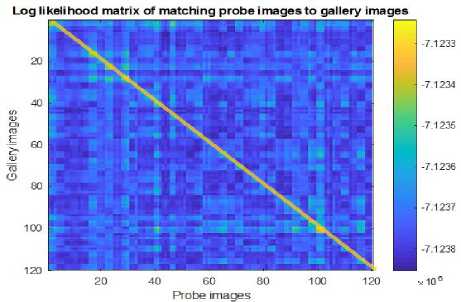
Fig.10. Log Likelihood Matrix of Probe Images vs. Gallery Images

It was also found that the dimensionality of latent variables also affects the recognition rate. Equal Error Rate (EER) which inherently mentions to error margin, a joint point where the false rejections are equal to and false acceptances. Figure 11 shows the equal error rate (EER) vs. the dimensionality of latent variables. EER reduces by increasing the dimensionality of latent variables. Initially, adding dimensions to the latent variables helps in decreasing EER as the information embedded in the added dimensions helps in reducing false acceptance rate. After reaching the value of 100, further increase in the dimensionality of latent variables does not reduce the EER.

UMIST database. We compare proposed approach with the basic dimensionality reduction approaches, uniform and non-uniform texture based descriptors, uniform and non-uniform texture based descriptors with dimensionality reduction approaches and PLDA. Table 1 shows the performance of the proposed scheme versus other approaches.

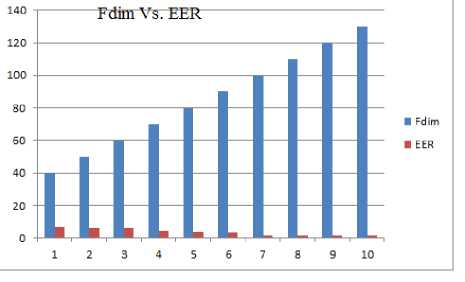
Fig.11. Equal Error Rate for different subspace dimension

Table 1. Recognition Accuracy Comparison

Approach Used	Average Accuracy(%)
PCA (65)	56
LDA (65)	59
LLE(65)	60.5
KPCA (Polynomial Kernel)	58.9
PCA+Bayesian (65)	66
Gabor+LBP	75
Gabor+LBP+PCA (65)	76.5
LBP+PCA(65)	69
LBP+PLDA	87
LBP+PCA+PLDA	89.7
HVDGBP+PCA	73.89
HVDGBP+KPCA+PLDA	92
HVDGBP+LLE+PLDA(*)	93.94

* Proposed Method

The reason for achieving impressive recognition rate can be attributed to the fact that when the data model is nearly a binary CIA (Conditionally Independent Attribute) model, then EM is able to converge faster and attains optimal performance.

• V.    Conclusion

In this paper, we propose the formulation of HVDGBP descriptor and then using PLDA models to find the similarities between identity-related gallery and probe images. While HVDGBP descriptor extracts the local texture details of face images, PLDA models explicitly search for the maximization of the correlated features to retain most informative content between the gallery and probe sets. PLDA attempts to model the difference between the classes of data, so its application helps in achieving better identity recognition even in the presence of pose variations. Since HVDGBP is based on LBP, its efficiency is not affected by intensity variations. Though PLDA application gives better identification rates, still it has the issue of retraining score model whenever a new subject is added to the training dataset. For the future works, we will explore other feature descriptors like a bag of words (BOW) with PLDA models.