Hybrid Cryptographic Approach for Data Security Using Elliptic Curve Cryptography for IoT

IoT is a developing technology that connects devices through the Internet for data sharing. Devices connected to the IoT are embedded with sensors that come under the umbrella of the IoT. It is based on the availability of numerous intelligent objects such as sensors, actuators, mobile devices, and RFIDs, all working together to achieve a shared goal. IoT is applicable to many different fields, including smart homes, smart cities, smart grids, smart cars, smart buildings, smart healthcare, smart farming, and many more. IoT networks are groups of different intelligent devices that are formally linked. IoT devices exchange data and offer services to one another through communication. IoT devices can be used for personal data sharing, which leads to massive volumes of data being generated every day. Sharing information among these devices is susceptible to a number of security flaws. The most difficult task in today’s society is to maintain data security for a large number of devices that are connected to the Internet of Things. In order to achieve secure data transmission in distributed IoT networks, IoT systems need some security techniques.

In the IoT setting, conventional cryptographic solutions are inappropriate. For encoding and decoding, conventional cryptographic methods (symmetric or public) are frequently used. In symmetric and public methods, there is a one-to-one communication between intended users. Generally, to deal with the confidentiality and authenticity of data, symmetric key encryption or public key encryption is majorly used. AES and DES are the most commonly used symmetric key algorithms. RSA, ElGamal and ECC are asymmetric key encryption algorithms that are used to maintain data security. Encryption algorithms are used to achieve the confidentiality of data, while MAC is used to achieve the authenticity of data. The availability of data cannot be achieved by using encryption algorithms.

One of the biggest drawbacks of symmetric cryptosystems is the key agreement procedure, in which users must agree on the same secret key through a secure communication channel in order to maintain confidentiality in the future. In the digital world, secret key sharing is suffering from various security attacks. In 1976, Diffie and Hellman [1] proposed a secure key sharing technique that could be used over an insecure communication channel to overcome this problem. This idea was the basis for the first step towards public-key cryptography, in which confidentiality of information sharing between parties is no longer required. Hard mathematical problems are considered to be computationally difficult, which provides security in public-key cryptosystems. As a result, adversaries are unable to obtain secret keys from public keys.

In general, cryptographic approaches are expensive in terms of execution time and storage. In IoT networks, achieving the reduction of processing power, storage capacity, and computational power is a difficult task. The deployment of complex security methods on resource-constrained devices is limited while using the traditional Internet. These issues are critical when it comes to ensuring data security in resource-constrained IoT devices. Therefore, the absence of proper security and privacy-preserving techniques has negatively impacted the widespread adoption of the IoT paradigm. Modern public-key cryptographic techniques are applicable in IoT networks to achieve data security. AES is one of the cryptographic techniques that are used to ensure data security while data transmission is done over various networks. ECC [2, 3] is a type of public-key cryptographic technique that uses a smaller key size to ensure security. ECC is a popular method for protecting data transfer across IoT networks.

Existing public-key cryptographic techniques have several limitations, such as key sizes and ciphertext sizes. In addition, most public-key cryptographic techniques involve modular exponentiation, which requires high computational resources. But in the IoT environment, devices have limited computational and communicational resources. These devices are suffering from various limitations, like limited computing power, storage and battery power. These challenges are overcome by a hybrid approach that is a combination of lightweight symmetric and public key cryptographic techniques.

Therefore, this paper provides a hybrid approach to maintain the security, confidentiality and authenticity of data. The main contributions of this paper are as follows:

• •    We present a hybrid approach by combining AES and ECC in which the elliptic curve Diffie-Hellman (ECDH) algorithm is used for key generation. In other words, key generation is done by using the ECDH algorithm, instead of AES, to reduce key size.

• •    Public/private key cryptography uses a key pair for encryption and decryption. As a result, both the larger key size and heavy processing power are needed for the encryption and decryption processes. The proposed scheme addresses the issue of key sizes and employs a smaller key to effectively increase system security. It also helps to lessen computing power for memory utilization.

• •    We use message authentication codes to achieve authentication of messages, and AES is used to achieve confidentiality of messages.

• •    We present the performance and security analysis of the proposed scheme in order to analyze its performance and security.

2.    Related Works 3.    Background

The rest of this paper is organized as: Section 2 reviews some related works. Section 3 provides some mathematical preliminaries. Section 4 gives the proposed scheme. Section 5 provides performance and security analysis. Section 6 concludes this paper.

An extensive literature review has been performed to study and analyze the basic workings of the AES algorithm, elliptic curve cryptography, and message authentication code of the various earlier proposed modifications by researchers. The AES algorithm was initially proposed by Rijndael [4]. After that, a lot of research has been done on the application of the AES algorithm to achieve security in an IoT environment. Al-Mashhadani and Shujaa [5] have used the AES algorithm to secure IoT systems. In this scheme, data generated by using a card is sent over the Internet, and this data can be accessed by authorized users only. Ahamed et al. [6] have presented a model to attain security in IoT systems using AES-256 and SHA-256. The information gathered from the devices has been first encrypted with AES-256 using a symmetric key, and then the ciphertext is produced. In order to transmit data securely, a new security measure known as the MQTT protocol has been included.

Yu et al. [7] have proposed a fake key-based AES approach to avoid considerable power and space overhead while preventing the secret key. Saraiva et al. [8] have presented a comparison of the execution time and power consumption of the AES and other algorithms in IoT devices. Makarenko et al. [9] have performed a comparative assessment of various symmetric block-based cryptographic algorithms to discover the best suitable algorithm for IoT applications. Rehman et al. [10] have proposed a technique using AES and ECC to maintain data security and integrity when data is transmitted over the cloud. Lara et al. [3] have proposed an acceleration engine using binary Edward curves, which are competent for use in resource-constrained devices. Kassab et al. [11] have presented an improved AES by changing the key expansion function. A hybrid and secure algorithm [12] have been proposed to enable end devices to encrypt the data using the AES algorithm before transmitting it to the cloud.

Dutta et al. [13] have surveyed lightweight cryptographic solutions, including AES, which can be used to achieve security in IoT. Masram et al. [14] have presented a comparative analysis of symmetric ciphers based on encryption. Dang et al. [15] have proposed an improved AES algorithm in which the key is dynamic in nature and it changes with encrypted data in a car tracking system. Su et al. [16] have optimized the AES and presented an improved data encryption standard to achieve better security in the IoT environment. Sultan et al. [17] have used the AES for secure communication in wireless sensor networks. Arpaia et al. [18] have presented an improved version of the signature analysis of sensor power consumption. Jat et al. [19] have proposed an improved AES algorithm to be applied in military networks and IoT applications. Arpaia et al. [20] have analyzed the results of a side-channel attack addressed to an 8-bit IoT microcontroller protected by AES.

Noor et al. [21] have presented a multipurpose encryption engine to process AES and CRC algorithms using a shared GFCU. Hussain et al. [22] have implemented the MAC algorithms for GOOSE message integrity. Based on a cryptographic hash function, Bellare et al. [23] have presented new constructions of message authentication schemes. Usman et al. [24] have proposed a secure IoT algorithm by combining Feistel and a uniform substitution-permutation network. A key scheduling technique [25] using a 3-dimensional S-box has been presented to apply to lightweight IoT devices. A communication method [26] has been proposed to reduce the power consumption of end devices by reducing the encryption cycles of AES. Mahmood et al. [27] proposed a hybrid authentication technique for session key generation using AES and RSA and the integrity of the message is achieved by using a hash-based MAC. Tsai et al. [28] proposed the AES encryption architecture to lessen the power consumption for data encryption. Rady et al. [29] have presented a hardware security module for implementing low-power IoT security.

The main purpose of the AES algorithm in the current situation is to protect data from unauthorized access. It is possible to securely store data in the cloud so that only authorized users may access it. When broadcast across secure or unsecured networks, data transmission in the IoT environment must be kept secure. In order to guarantee security in the dynamic IoT context, classical cryptographic solutions typically incorporate both symmetric and public key cryptography. These cryptographic solutions require practicable infrastructures. Creating a secure infrastructure is a challenging task for secure data sharing among heterogeneous devices. In addition, combining symmetric and asymmetric key cryptography in order to build a new hybrid cryptosystem is also a challenging task. Therefore, it is necessary to create a secure hybrid cryptographic technique using AES and ECC to transmit the data through insecure channels in IoT environments. Table 1 gives the acronyms and their definitions. Table 2 gives the notations and their meanings used in this paper.

In this section, we give some useful mathematical backgrounds which are used in this paper. We also provide an overview of the AES algorithm.

• 3.1.    Elliptic Curve Cryptography

Koblitz [2] has firstly introduced the definition of ECC. Let IE be the elliptic curve (EC) over a finite field Ep is given by a cubic equation

Y2 =  Х3 + aX + b (mod p), where, 4a3 + 27b2 * 0 and a,be %p.(1)

• A.    Addition of Points

Let К — (Х_К, Y_k) and К = (Х_К, Y_K) be the points on E

Y2 = X3 + aX + b (mod p)(2)

Addition of points К and К can be calculated as

К+ К - P - (XP,YP)(3)

• , v - 12  v   v  v - w v \            №xh + a}/2YK,       if К -К.

where, X A   Х.  Xx, yp - № — Xp} - Y^ and A - {(Yk - Yk)/(Xk - Xk),  if К *К .

All hold for the case that Л * и; otherwise P - и.

• B.    Scalar Point Multiplication

Suppose R be a point on an elliptic curve IE and к is an integer. Then the scalar point multiplication of R by к is the point к • R that is computed as k^R = R + R+......+R, ifk>0

k-R = (-kX-R^ if k<0

Table 1. The list of acronyms

Acronym	Definition
AES	Advanced Encryption Standard
CS	Cloud Server
DES	Data Encryption Standard
DO	Data Owner
DU	Data User
EC	Elliptic Curve
ECC	Elliptic Curve Cryptography
FPGA	Field Programmable Gate Array
GOOSE	Generic Object- Oriented Substation Events
MAC	Message Authentication Code
MQTT	Message Queuing Telemetry Transport
RSA	Rivest, Shamir, Adleman
GFCU	Galois Field Computation Unit
CRC	Cyclic Redundancy Check

Table 2. Notations and meaning

Notation	Meaning
E	Elliptic curve over a finite field Fp
G	Generator point of elliptic curve E
F ₽	Finite field
∞	Point at infinity (zero element) of E
^ p	A field of integer modulo p
a,b	Coefficients of elliptic curve E
n	Order of the subgroup
h	Cofactor of the subgroup
Kx	Encryption and decryption key
Ky	MAC key
Enc	Encryption
Dec	Decryption
К	Finite set of possible keys
M	Set of possible messages
T	Finite set of possible authentication tags

• 3.2.    Elliptic Curve Discrete Logarithm Problem (ECDLP)

• 3.3.    Overview of AES

Suppose E be an EC defined over a finite field E_p, where p is a prime number. The ECDLP can be defined as for given P,Q £ E, compute an integer number n such that Q = n • P in the group E. The ECDLP is harder than DLP.

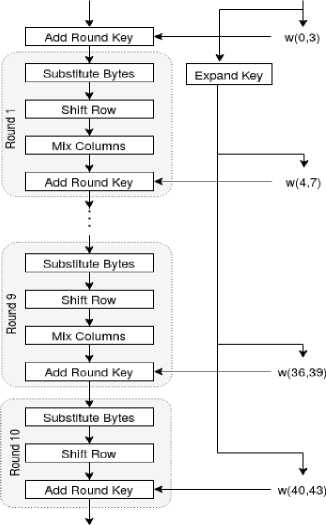
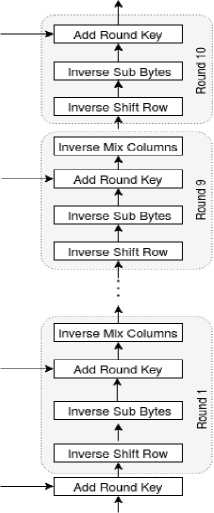
The AES Algorithm is a block cipher algorithm that encrypts and decrypts 128-bit data blocks using 128, 192, and 256-bit encryption keys. AES consists of IP rounds, where ЛТ = 10 for a 128-bit key length, ЛТ = 12 for a 192-bit key length, and P = 14 for a 256-bit key length. Here, we consider the 128-bit key AES to perform the processes of encryption and decryption. In the AES encryption, there are 10 rounds to be performed. In every round of the first 9 rounds, four transformations are executed on data in the state of encryption. In round 10, only three transformations are executed on data in the state of encryption. Similarly, in the AES decryption, there are 10 rounds to be performed. In every round of the first 9 rounds, four transformations are executed on data in the state of decryption. In round 10, only three transformations are executed on data in the state of decryption.

Description of the AES Algorithm

In the key expansion operation, Rijndael key table is used to derive round keys from the cipher key. Fig.1 illustrates the process of encryption and decryption of AES. In the proposed scheme, we use a 128-bit key length to perform the process of encryption and decryption. Therefore, it needs H = 10 to perform the processes of encryption and decryption. In each round, four transformations are executed, and in the last round only three operations are executed. In the process of encryption, the first nine rounds include the four operations (Substitution Bytes, Shift Rows, Mix Columns and Add Round Key) and the final round includes three operations (Substitution Bytes, Shift Rows and Add Round Key). Similarly, in the process of decryption, the first nine rounds include four operations (Inverse Substitution Bytes, Inverse Shift Rows, Inverse Mix Columns, and Add Round Key) and the final round includes three operations (Inverse Substitution Bytes, Inverse Shift Rows, and Add Round).

Plaintext

Key

Ciphertext

Plaintext

Ciphertext

Fig.1. AES encryption and decryption

Now, we will describe various transformations Substitution bytes, Shift Rows, Mix Columns and Add Round Key to understand the functionalities.

• •    Substitution Bytes : In this phase, the state array’s bytes are split into two equal portions and converted to hexadecimal. These components -rows and columns - are mapped using a substitution box (S-Box) to create new values for the final state array. The initial operation in each run of execution is (Sub Bytes and InvSub Bytes), which replaces every bite of the state with a byte of nonlinear S-box and Inverse S-box. The intercept must be utilized in the table to determine the replacement value. Plaintext and ciphertext connections are concealed using Sub Bytes and InvSub Bytes. Fig. 2 shows the substitute byte transformation of AES.

• •    Shift Rows : In shift row transformation, each row of the matrix is shifted from left to right. Any entries that fall off are re-inserted on the right side of the row. Shift rows transformation takes place as follows. The first row is not shifted and it will be the same as before. There is a one-position leftward movement in the second row. Two positions leftward movement in the third row. Three positions leftward movement in the fourth row. The outcome is a new matrix made up of the same 16 bytes but with their positions altered. Fig. 3 shows shift rows transformation of AES.

• •    Mix Columns : Now, a unique mathematical function is utilized to change every column of four bytes. The four bytes of one column are entered by this function, which returns four entirely new bytes that replace the original column. The outcome is another new matrix with 16 new bytes. The final round does not include this phase. The AES mix columns transformation is depicted in Fig. 4.

• •    Add Round Key : The 128 bits of the round key are XORed with the 16 bytes of the matrix, which are now thought of as 128 bits. The output is the ciphertext if this is the final round. If not, the resulting 128 bits are translated into 16 bytes, and the process starts all over again. Fig. 5 depicts the AES add round key transformation.

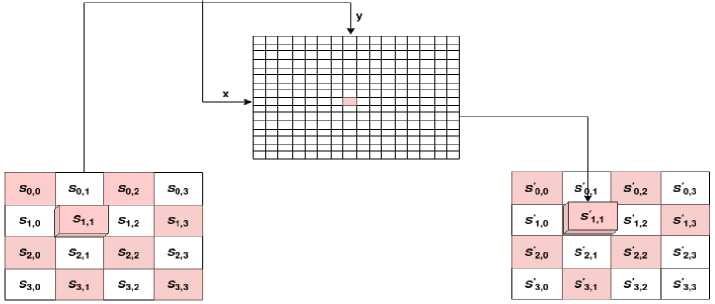
Fig.2. Substitute Bytes transformation

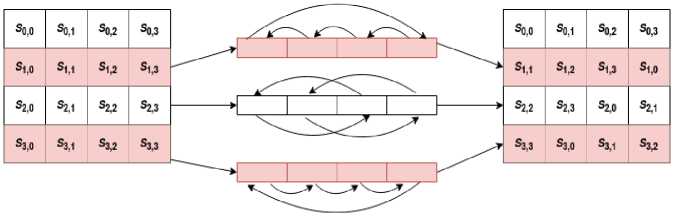
Fig.3. Shift row transformation

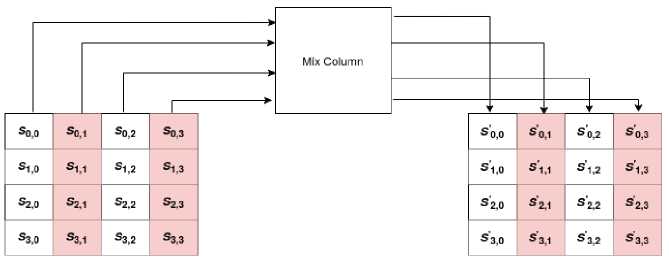
Fig.4. Mix column transformation

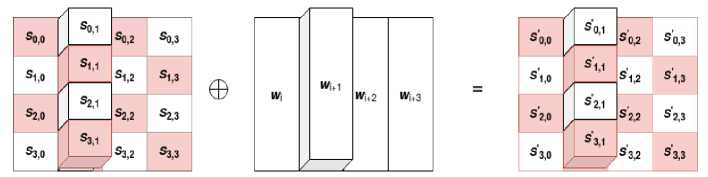
Fig.5. Add round key transformation

4.    Proposed Scheme

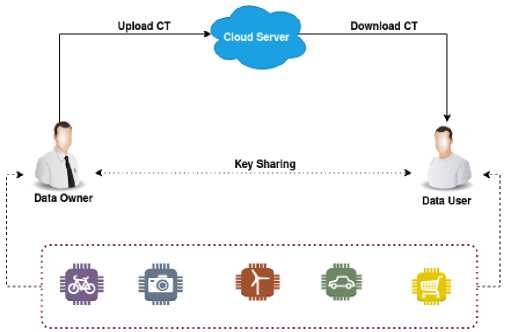
In this section, we first describe the system model that defines various entities participating in the system. It also defines the functionalities performed by various entities. Then, we describe the proposed scheme in detail to understand its functionalities. Fig. 6 shows an overview of the system model for the proposed scheme.

• 4.1.    System Model

In our proposed scheme, there are mainly three entities that participate in system model. Data Owner (DO), Data User (DU) and Cloud Server (CS) are three entities. In our setting, DO and DU may be considered as one of smart devices connected to IoT networks.

• •    Data Owner : DO uses an encryption key to encrypt the data and sends it to the cloud server. The user who has

the valid decryption key can decrypt the ciphertext.

• •    Cloud Server : The CS can store the encrypted data. The CS is responsible for ensuring the availability of the encrypted data for the data user.

• •    Data User : DU downloads the ciphertext from CS. Then, DU decrypts the ciphertext using the decryption key. The decryption of ciphertext is possible only if DU has a valid decryption key.

  

• 4.2.    Construction of Proposed Scheme

Fig.6. System model

In the proposed scheme, we consider a hybrid cryptographic setting in which mainly three entities are participating in the communication. DO, CS and DU are the three main entities that create the system to communicate with each other. DO and DU are considered as IoT devices. In a symmetric key setting, DO sends the message to DU by using the public available channel. First of all, both of them agree on system parameters, based on the ECC, required for the transmission of the message. DO uses public parameters to generate the public and secret keys. Similarly, DU uses public parameters to generate public and secret keys. Therefore, DO and DU share a key using the ECDH key exchange algorithm. DO performs the process of encryption of a message by using the secret key and then stores the encrypted message over the cloud server. Then, DU can download the ciphertext and decrypt it. To retrieve the message, DU uses the private key to decrypt the ciphertext. If DU has a valid secret key, then he can retrieve the message successfully. Otherwise, he is unable to retrieve the message.

In the proposed scheme, a hybrid cryptographic approach is achieved by using a combination of public and private key cryptographic techniques. ECC is a best known public key cryptography, whereas AES is also a well-known symmetric key cryptography. In the proposed scheme, there are three stages 1) Key Generation; 2) AES Encryption and Decryption, and 3) Message Authentication Code. In the first stage, the key generation process is done by using the ECDH key exchange algorithm. The output of the key generation algorithm is a point that lies on the elliptic curve IE. This point can be seen as a tuple (K_x,K_y). The K_x is known as the encryption/decryption key and K_y is known as the MAC key. Second, after key generation, we use the AES algorithm to encrypt and decrypt. The K_x is used as the encryption key for the AES encryption process, and K_x is used as the decryption key in the AES decryption process. Finally, we also check the message authentication code of the message by using the MAC key K_y that was generated in the key generation phase. Fig. 7 shows the block diagram of the proposed scheme. A detailed explanation of the proposed scheme is given.

• A.    Key Generation

The elliptic-curve Diffie-Hellman algorithm is a key exchange protocol that allows two parties (say, Data Owner and Data User) to exchange a secret key over an insecure communication channel. Here, we describe the steps for exchanging the secret key between data owner and data user. The elliptic curve various parameters (p, a, b,Q, n, h) are considered for implementation. Here, p is a large prime number, a, b are curve coefficients, Q is generator point of elliptic curve, n is subgroup order and h is subgroup co-factor. The key generation procedure takes place between data owner and data user as follows.

• •    Data owner and data user have agreed on the elliptic curve which is defined by a set of domain parameters (p, a, b, Q, n, h).

• •    Data owner selects a secret integer a_D0 £ [1, p — 1] and computes a public key A_D0 = a_D0 ■ Q.

• •    Data user selects a secret integer b_DU £ [1, p — 1] and computes a public key B_DU = b_DU ■ Q.

• •    Data owner and data user exchange their public keys: A_D0 and B_DU.

• •    Data owner computes scalar multiplication, K_shared = a_D0 ■ B_DU=a_D0 ■ b_DU ■ Q and derives a shared secret key ^K shared = ^a D0 ■ ^b DU ' ^Q.

• •    Data user computes scalar multiplication, K_shared = b_DU • A_D0 =b_DU • a_D0 • £ and derives a shared secret key ^ shared = ^a D0 • ^b DU • S^.

• •    Now, both data owner and data user have the same shared key K= K_shared = (K_x, K_y) = a_D0 • b_DU • Q.

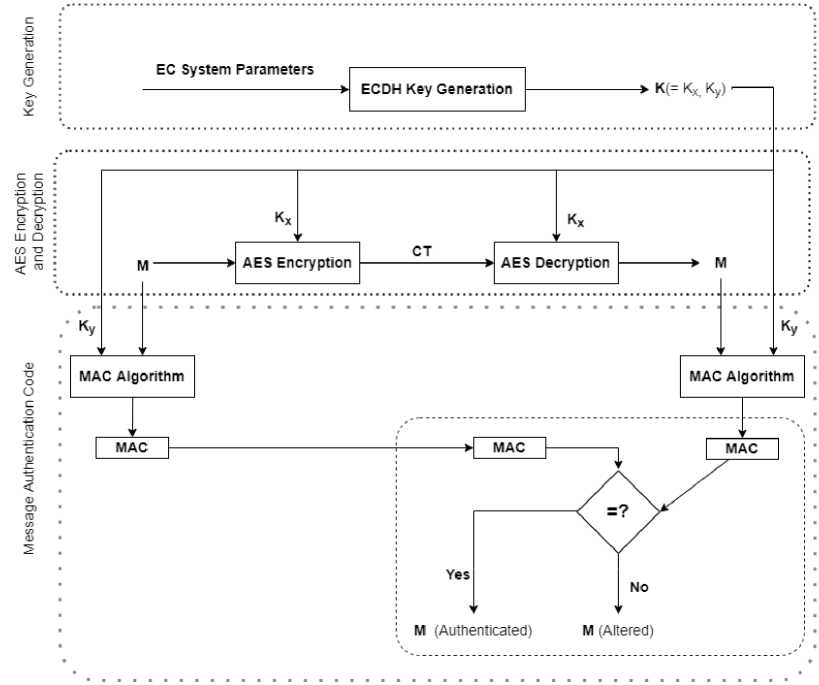
Fig.7. Block diagram of proposed scheme

The ECDH key exchange algorithm generates the secret shared key. This secret shared key, K_shared is a point that lies on the elliptic curve. Therefore, we split it into two parts namely K_x which is the x-coordinate of that point, K_shared and and K_y which is the y-coordinate of that point. Now, the secret key K_x is utilized for encryption of messages using the AES algorithm. Similarly, the secret key K_x is also utilized for the decryption of ciphertext using the AES algorithm. DO uses the secret key K_y as the MAC key to calculate the MAC of the message. Similarly, DU uses the secret key K_y as the MAC key to check the authenticity of the retrieved message.

• B.    AES Encryption and Decryption

AES Encryption : In the proposed scheme, a cipher consists of 10 rounds and a 128-bit key size is considered. Data owner first selects a message M from the message space ^. Then, he considers the encryption key K_x that was generated from the ECDH algorithm. In the first ^ — 1 rounds, distinct transformation functions Substitution Bytes, Shift Rows, Mix Columns and Add Round Key are performed subsequently. In the final round, only three transformation functions, Substitution Bytes, Shift Rows and Add Round Key are performed. Therefore, the ciphertext ( CT) can be calculated by using the encryption key K_x . The encryption process can be seen as follows.

• •    Data owner first selects a message M.

• •    Data owner considers a key K_x as encryption key which is generated by the ECDH key exchange protocol.

• •    Data owner encrypts the message M as CT = Enc_Kx(M) using AES encryption method.

• •    Finally, data owner sends the ciphertext CT to the cloud server to store it.

AES Decryption : Data user first downloads the ciphertext CT from cloud server and then decrypts it by applying his decryption key. AES decryption process can be described as: DU considers the ciphertext of 128-bit and a decryption key k_x that was generated from ECDH algorithm. In the first ^ — 1 round, four operations Inverse Shift Rows, Inverse Substitution Bytes, Add Round Key and Inverse Mix Columns are performed. In the final round, only three operations Inverse Shift Rows, Inverse Substitution Bytes and Add Round Key are performed. Therefore, the message is retrieved by using the decryption key K_x. The AES decryption process can be seen as follows.

• •    Data user first downloads the ciphertext CT from cloud server.

• •    Data user considers the decryption key K_x which is generated by ECDH key exchange protocol.

• •    Data user computes the message as M = Dec_Kx(CT) using AES Decryption method.

• •    Finally, data user gets the original message M.

• C.    Message Authentication Code

Consider a scenario where two entities (say DO and DU) are communicating with each other. Suppose DO wants to send the message to DU using a symmetric key setting over the insecure communication channel. This communication suffers from the alteration of transferred messages. Therefore, message authentication can be achieved by using various techniques like message encryption, message authentication code and hash functions. The SHA-256 algorithm [30] is used as the cryptographic hash function. The message authentication technique checks the authenticity and confidentiality of a message. MAC is a technique that uses a secret key to generate a fixed length code. In this technique, DO and DU share a secret key K_y known as the MAC key. The steps involved in the calculation of MAC are given as follows.

• •    Data owner selects a message M.

• •   Data owner considers a key K_y as the MAC key.

• •  Data owner computes MAC of as M as MAC = MAC_Ky(M) using the MAC key K_y .

• •    Data owner sends the MAC to data user.

• •    After receiving the MAC, data user computes MAC of as M as MAC = MAC_Ky(M) using the MAC key K_y.

• •    Finally, the data user compares the computed MAC with the MAC received from the data owner.

• •    If both MACs are equal, then the message is authenticated. Otherwise, the message is altered.

5.    Performance and Security Analysis

• 5.1.    Performance Analysis

The data owner first selects a message M and considers K y as the MAC key which is generated by the ECDH key exchange algorithm. After that, the data owner computes the MAC of the message M with the help of the MAC key K y and MAC algorithm. Now, the data owner sends the MAC to the data user. Similarly, the data user takes a message M and considers K y as the MAC key which is generated by the ECDH key exchange algorithm. Then, the data user computes the MAC value of the message M with the help of the MAC key K y and MAC algorithm. After receiving the MAC, the data user compares the computed MAC with the MAC received from the data owner. If the condition is true, then it returns that the message is authenticated. Otherwise, the message has been altered.

In this section, we first present the performance analysis of the proposed scheme. Then, we present the security analysis of the proposed scheme based on different security assumptions.

In IoT systems, most of the devices have limited storage or computational power, and meanwhile, due to the heavy computational operations used in various traditional public-key cryptographic systems, the data to be stored is usually relatively huge. Here, the storing of all parameters related to the system is considered as storage overhead. The complexity of storage can be reduced by using ECC. The data owner stores the encrypted message over the cloud server which reduces storage complexity. Storing data is also beneficial to the data user because there is no requirement to store data locally on the data user’s side. The storage overhead is mostly contributed by the public parameters and secret keys for data owners and users.

Table 3. Key size comparison of ECC and RSA

Security Strength	ECC key size	RSA key size	Ratio ECC to RSA
80 bits	160 bits	1024 bits	3:1
112 bits	224 bits	2048 bits	6:1
128 bits	256 bits	3072 bits	10:1
192bits	384 bits	7680 bits	32:1
256 bits	521 bits	15360 bits	64:1

To analyze the computational time of various processes of cryptographic techniques, hardware specification Intel(R) Core (TM) i7-3770 CPU at 3.40 GHz and 4GB RAM are used. The system runs Ubuntu 16.04 LTS operating system. The implementation uses an elliptic curve У² = X³ + 7 over a finite field with 128 bits of security. The main advantage of using ECC is its smaller key size and it provides the same security level compared to other public-key cryptographic techniques. Table 3 shows the key size comparison of ECC and RSA [31].

Computing efficiency is analyzed by the estimation of various operations. In this paper, computational time refers to encryption and decryption times. We analyze the computational efficiency of the proposed scheme to complete the encryption and decryption processes. Encryption and decryption times are measured in milliseconds (ms). The data sizes are measured in kilobytes (KB). We analyze encryption and decryption times performed by the data owner and data user respectively. Generally, the public key cryptographic approach requires more time to complete the various processes involved in the cryptographic algorithm. Therefore, we use symmetric key cryptography using ECC to reduce the computational time of encryption and decryption.

We have considered different data sizes for the comparison of our proposed scheme with other existing schemes. We consider various instances of data sizes of 2 KB, 4.1 KB, 6.1 KB, 8.2 KB, and 10.2 KB to calculate the encryption time and decryption time. Fig. 8 shows the comparative computational time taken by various cryptosystems to complete the encryption. According to Fig. 8, the hybrid scheme takes less time to complete the encryption process as compared to traditional AES and DES. Moreover, the proposed scheme provides higher security and makes the system secure against various attacks. The encryption time of the proposed scheme is comparatively less than other existing algorithms. Fig. 9 shows the comparative computational time taken by various cryptosystems to complete the decryption process. According to Fig. 9, the proposed scheme takes less time to complete the decryption process as compared to traditional AES and DES. The decryption time of the proposed scheme is comparatively less than other existing algorithms. Therefore, the proposed scheme shows a better computational time as compared to the existing algorithm.

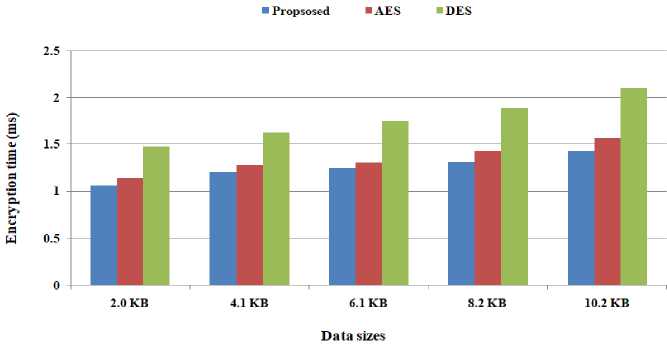
Fig.8. Encryption time taken by various algorithms

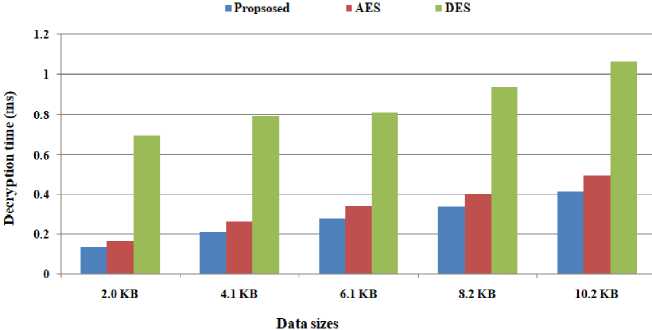
Fig.9. Decryption time taken by various algorithms

ECC is the technique that guarantees the security of the data stored in the cloud. Maintaining data with smaller keys can help to maximize the storage capacity and get optimal results. ECC uses the smaller key sizes as compared to RSA. The main advantages of using ECC are the smaller key sizes and the encryption is done by using the public key. Compared to RSA, ECC shows better results in data encryption and decryption. In the proposed scheme, MAC provides the authenticity of data to ensure the originality of received data. Therefore, our proposed scheme provides higher security with smaller key sizes as compared to other cryptographic techniques. Our scheme also reduces computational complexity and optimizes the storage capacity. Thus, a higher level of security can be achieved by using smaller key sizes. Therefore, the proposed scheme shows better results in terms of computational complexity as compared to others.

• 5.2.    Security Analysis

Here, we present the security analysis of the proposed scheme. The key generation process is done by using the ECDH key algorithm. So, the security of ECDH depends upon the hardness of ECDLP. Further, the AES algorithm is used for encryption and decryption, and the security of AES depends upon the number of rounds used in the AES algorithm. Finally, we calculate the MAC of the message for authentication and its security depends upon various factors. We describe the security of the proposed scheme as follows.

• A.    Security of ECDH Algorithm

The security of the key generation phase of the proposed scheme is based on the elliptic curve discrete logarithm problem. In the proposed scheme, key generation is done by using the ECDH key exchange protocol. Therefore, the security of the key depends on ECDLP. Suppose IE be an EC defined over F_p. Consider Q is a generator of an elliptic curve E. Data owner chooses a secret integer a_D0 and calculates a public key A_D0 = a_D0 • Q. Data User chooses a secret integer b_DU and calculates a public key B_DU = b_DU • Q. Data Owner and Data User exchange their public keys: A_D0 and B_DU . Data owner computes another scalar multiplication, K_shared = a_D0 • B_DU =a_D0 • b_DU • Q and derives a shared secret key K_shared = a_D0 • b_DU • Q. Data User computes another scalar multiplication, K_shared = b_DU • A_D0=b_DU • a_D0 • Q and derives a shared secret key K_shared = a_D0 • b_DU • Q. Suppose an adversary has access to these public keys A_D0 and B_DU. The adversary also has access to the elliptic curve parameters used in the system. From public keys A_D0 and B_DU, the adversary is not able to compute the private key of data owner and data user. Data owner and data user will not reveal their private keys used for generating public keys. As per the hardness of ECDLP, the computation of secret key a_D0 from A_D0 or secret key b_DU from B_DU is infeasible. The knowledge of a secret key means the adversary can solve the ECDLP. Therefore, the security of the ECDH key exchange algorithm depends upon the hardness of ECDLP.

• B.    Security of AES

  The AES algorithm is renowned for being secure against all known vulnerabilities. Specific features are incorporated into various design elements to provide protection against particular threats. For instance, using the finite field inversion procedure to build the S-box results in linear approximation and difference distribution tables with nearly uniform entries. This offers protection against linear and differential attacks. Evidently, there are no known "generic" AES attacks that can outpace an exhaustive search. The adversary is given ciphertexts that have been encrypted using two or more unknown keys that have a certain relationship between them in a related key attack. The NIST selected three categories of AES including 128-bit, 192-bit, and 256-bit. Every version of AES uses 128-bit blocks and the length of the key only differs. AES-256 provides a strong level of encryption. The adversary has to try 2²⁵⁶ different combinations to get the correct key with a 256-bit key. The number of encryption rounds distinguishes the three AES variants. The complexity of the encryption increases with the number of rounds. Therefore, AES 256 is considered as the most secure version. It would be ridiculous for the adversary to even attempt this kind of attack. The primary risk appears to come from side-channel attacks because the AES cipher is so secure on its own. This aims to gather information from leakage of the system rather than making a brute-force attack. An adversary may monitor sounds, electromagnetic signals, time data, or power usage in an effort to learn how security algorithms perform. By eradicating information leaks or concealing the leaked data to prevent it from revealing any relevant information, sidechannel attacks can be avoided. These side-channel vulnerabilities can be avoided by carefully implementing AES. Security professionals maintain that AES is secure when used correctly. AES encryption keys must be secured. If a hacker obtains the encryption key, the most robust cryptographic systems may be vulnerable.

• C.    Security of MAC

6.    Conclusions

Brute-force attacks on MAC are a difficult task as compared to a brute-force attack on a hash function because they need known message-tag pairs. We describe the attack on a hash code: Let h = H(M) be defined as an n-bit hash code for a fixed message M. Now, the brute-force method is to find a collusion by picking a random bit string у and checking if H(y) = H(M). An adversary is allowed to do this repeatedly. Whether an adversary can apply MAC algorithm that is dependent of the retrieve size of the key and the tag. The main objective of an adversary is to generate a message-tag pair (M,MAC(K,M)) that is valid under a fixed but unknown key K. Suppose an adversary has some message-tag pairs (M i , MAC(K, M i )) that are valid for the key K. Consider these i message-tag pairs might be ones that an adversary has observed while transmitting from data owner to data user. This condition is called a known message attack (KMA). In KMA, the messages M i are known to the adversary, but the data owner will decide which messages to transmit to the data user. In chosen message attack (CMA), the adversary is allowed to select the messages M i and then make queries to data owner for the corresponding tags MAC(K,M i ).

Consider a scenario where the adversary can get a list of message-tag pairs (Mi,MAC(K,Mi)) which are valid under the same unknown key K. Then, the adversary produces a message-tag pair (M,MAC(K,M)) for a new message M. But M is not a valid message if M ^ Mi. If pair (M,MAC(K,M)) is a valid pair then, it is called to be a forgery. If the adversary produces a forgery with a probability (at least) e, then the adversary is called an (e, i)-forger for the given MAC. In CMA, the adversary can make queries for maximizing the probability of a successful attack. In KMA, the messages are beyond the control of the adversary, and the adversary will succeed with probability at least e. Finally, the probability e of a successful forgery could be considered to be either an average-case probability over all the possible keys, or the worst-case probability. Consider e to be a worst-case probability means the adversary can generate a forgery with probability at least e, regardless of the secret key being used. These attacks described above are known-message (1,1)- forgers. At last, we describe two attacks, namely the key space attack and MAC value attack. In the key space attack, the adversary chooses К E К uniformly at random, and outputs the tag hK(M) for an arbitrary message M. This attack will succeed with probability 1/|К|. In the MAC value attack, the adversary chooses the tag MAC(K, M) E T uniformly at random and outputs MAC(K,M) as the tag for an arbitrary message M. This attack will succeed with probability 1/|T|.

In the IoT environment, lightweight IoT devices have limited storage and computational processing capabilities. Therefore, there is a need to store data on the cloud server to reduce the storage capacity. However, storing data on a cloud server has a number of security flaws. Therefore, to ensure security and reduce computational complexity, a hybrid cryptographic approach is proposed by using AES and ECC. The scalar point multiplication operation of ECC is used to reduce computational complexity. AES is a lightweight cryptography approach that provides security along with a smaller key size. The combination of AES with ECC performs better to provide data security. In the IoT, the performance of resource-constrained devices has been enhanced by applying the lightweight properties of ECC. The message authentication code also achieves confidentiality and authenticity of the transferred message. In the future, applications of various cryptographic techniques, including AES and ECC, can reduce storage and computational overheads in the IoT. This research may encourage researchers to develop new security schemes with effective performance in the context of the IoT by applying lightweight cryptographic techniques using ECC.