Hybrid Spider Monkey Optimization Mechanism with Simulated Annealing for Resource Provisioning in Cloud Environment

Cloud computing is characterized as the abstraction of information from the user, requiring no additional technical knowledge. It is regarded as a creative complement, usage, and dissemination prototype for Internet-based information technology services [1]. Cloud computing is a revolutionary concept that allows cloud users to access resources offered by the cloud service provider, allowing them to make greater use of numerous distributed resources. A fundamental challenge in the cloud computing system is how resources are assigned to customers with minimal execution time and effectively. As a result, the primary goal is to offer resources with the shortest possible execution time while maintaining high performance, also considering the growing need for computing resources.

The mechanism for provisioning resources in a cloud environment is called resource provisioning. It carries out provisioning in accordance with client demands. Both options are available to customers who wish to pay a bill in advance for needed resources or a bill based on actual consumption. The main aspect to look out for a while executing resource provisioning is to prevent over and under-provisioning of resources. Under provisioning refers to resources supplied to customers that are insufficient for their needs, whereas over-provisioning refers to resources that are excessive and not needed by users [2, 3]. Therefore, it's important to deliver resources on time and in accordance with user needs in order to ensure efficient resource provisioning.

This paper aims to provide a hybrid HSMOSA strategy to ensure effective resource provisioning. This is a hybridization of simulated annealing with spider monkey optimization. In their respective fields, simulated annealing and spider monkey optimization are both significantly beneficial. As a result, we assessed the features of both methods and produced HSMOSA, a hybrid algorithm that increases throughput and efficiently allocates resources with minimum processing time. Comparison with the current PSO-SA method is also included to show the effectiveness of the proposed methodology. This PSO-SA is an existing hybrid resource provisioning strategy [4]. Following are the main goals of this paper:

• •    To minimize the execution or provisioning time of resources.

• •    To optimize the fitness value of task, this leads to improve their position.

• •    To increase the throughput and improve the performance of allocating resources.

• •    To address the resource provisioning problems of over and under-provisioning.

• •    To perform the better provisioning of resources as compared to the existing method.

2.    Related Works

Improve the overall efficiency of resource providing by accomplishing the aforementioned objectives. This facilitates improved resource provisioning in a cloud environment. Simulation data are presented to explain how the suggested HSMOSA technique performs in a cloud environment. The next section shows the literature review related to resource provisioning and meta-heuristics technique.

Swarm intelligence encompasses a variety of optimization strategies, including SMO, a recently population-based technique employed on spider monkey group interactions. It is derived from spider monkeys' foraging intelligence behavior, reflecting the fission-fusion social system (FFSS). Individuals in FFSS form temporary small groups whose individuals are members of a larger or more stable created and popular technique that has established its place among the group of optimization techniques. SMO is society. Monkeys partition themselves into groups based on the lack of available food sources. These groups may be larger and smaller. The global leader is considered the leader of the entire group, and a local leader is assigned to smaller groups. Spider monkey optimization includes six phases [5], which are as follows:

• •    Local leader phase: All spider monkeys can update themselves at this phase. The fitness value of each spider monkey is used to generate a new position. If each spider monkey's newly determined fitness value is better than the previous fitness value, the position should be updated; otherwise, it should not.

• •    Global leader phase: The solution is updated based on the fitness function and probability in this phase. Use the greedy strategy to identify the best value and update the solution.

• •    Global leader learning phase: In this phase, compare the improved fitness value to determine the global leader from the complete solution. If the global leader's position is not changed, the global limit count is increased by one. Set 0 otherwise.

• •    Local leader learning phase: This phase is very similar to the one before it. Increase the global count if the local leader's position has not been refreshed; otherwise, set 0.

• •    Local leader decision phase: This is essentially a choosing phase to use the local limit counter and, if necessary, re-initialize the local leader if there is any early convergence in the group.

• •    Global leader decision phase: To avoid premature population convergence, the global leader must make a vital decision at this phase. If required, split the population into groups and then reunite in the end.

Simulated annealing is based on the general annealing idea, in which a system is slowly cooled until it reaches a minimal energy state where it is vital. This approach performs better when dealing with optimization problems because it involves annealing. The objective function was also employed to optimize the solution in this approach. It begins at T, the starting temperature. Then calculate a new solution and compare it to the previous one; if the new solution has a lower value than the previous one, accept it. If the new solution has the highest value, perform an exponential calculation and generate a random number. Accept the new solution if the random number is smaller than exponential; otherwise, reject it.

expon = e(-∆f/T)                                               (1)

∆f=change value of an objective function

T represents the temperature.

In the SA procedure, randomly generate an initial solution.

The system's temperature significantly influences the actual annealing process's temperature.

In SA, most worsening moves may be picked in the beginning, but only improving moves are allowed at the end [6, 7].

To address the allocating issue of cloud services, an autonomous resource provisioning and scheduling architecture were proposed. The multi-objective optimization problem was solved by combining the spider monkey optimization algorithm with this framework. The efficiency of this scheduling system was demonstrated via simulation results [8]. In virtualized cloud data centers for service providers and users, a novel strategy is developed to help minimize energy costs and optimize revenue. A proposed smart controller achieves fine-grained resource provisioning. Furthermore, a novel hybridization of particle swarm optimization with simulated annealing [9] is used to address the profit maximization problem. An ePower mechanism is introduced to improve the system throughput and manage power consumption regarding green power supply [10].

The suggested cloud Assisted Mobile Edge (CAME) virtualization technology boosts the edge platform's scalability. The proposed optimal resource provisioning (ORP) scheme with various instances improves the edge hosts' processing power [11]. ElasticNFV is suggested for Virtual Network Functions. Its two-phase minimal migration technique reduces migration time and VNF embedding cost minimization [12]. A TIMER-Cloud framework is suggested to prioritize user requests according to their resource needs and deadlines [13]. An extensive survey is offered to identifying significant research challenges and real-time computing paradigms [14]. An AFSMO method was designed to address the Spider Monkey Optimization technique's stagnation and slow convergence concerns. This AFSMO approach featured an accelerative component that improved the core SMO algorithm's global and local leader phases [15]. The electromagnetic and antenna communities employed spider monkey optimization. To demonstrate the SMO algorithm's value, it was compared to other traditional optimization methodologies [16]. To solve the multilevel planning and scheduling problem, the HSMO method is introduced for parallel PCB assembly lines. According to the experiment results, the HSMO methodology can produce a better optimal solution than other traditional methods [17].

A spider monkey crow optimization strategy based on a sentiment categorization form is presented toward deep recurrent neural network training. It essentially employs telecom review to reduce user searching time by eliminating step words and excluding extraneous information [18, 19]. SMDs have been shown to use less overall energy using a partial compute offloading scheme (Smart mobile devices). A novel hybrid meta-heuristics paradigm is used to resolve non-linear constrained optimization [20]. The suggested green cloud computing paradigm separates the problem of virtual machine deployment from the issue of job scheduling. A CESCC approach is presented to forecast the potential workloads of the system. According to the experiment findings, prediction enhances real-time response efficiency and system stability, and conservative control procedures catch up with resource pre-allocation demands [21]. To reduce total makespan and cost of multiple-workflow scheduling, an MCHO mechanism is offered. Initially, a multi-swarm co-evolutionary process was built, with three swarms searching for various elite answers. Second, it includes local and global guiding information from particle swarm optimization to increase global search and convergence performance. Finally, to use more non-dominated individuals, a genetic algorithm-based elite augmentation strategy has been devised [22]. Added probabilistic sampling of simulated annealing to the PSO algorithm to improve the PSO-SA algorithm's limitation. It aids in maintaining population diversity and avoiding falling into the optimal local solution [23].

To address service discontinuity in mobile edge computing, an effective edge intelligent service placement algorithm (EIPSA) is presented [24]. To manage and overcome premature convergence of resource allocation in mobile edge clouds, an FSAOS (fruit fly-based simulated annealing optimization strategy) has been developed. The usefulness of the FSAOS approach was demonstrated in this global and local search balance utilizing simulated annealing EdgeCloudSim simulation results [25]. Exponentially spider Monkey optimization (E-SMO) is presented for effective resource allocation to reduce power consumption and improve service quality. It's a spider monkey optimization paired with an exponential weighted moving average [26]. By lowering the number of integrated web services, the Multi-Stage Forward Search (MSF) method is used to improve the processes of web service selection and composition. This model employs the spider monkey optimization technique to improve services. Experimental results demonstrated that the suggested SMO method outperformed the innovative multistage forward search technique [27]. The importance of the simulated annealing method in the traveling salesman problem is discussed to determine the best route between items. The primary objective is to use mathematical models to identify the shortest path between the various items [28].

3.    Proposed Hybrid Algorithm (HSMOSA)

To correctly provision resources in a cloud context, proposed the HSMOSA hybrid approach, which integrates Spider Monkey Optimization with the Simulated Annealing algorithm. This work used SMO to search local and global, and SA to search around global best after finding global and local best. Let's look at it another way, local best and global best have a better chance of increasing fitness value. This hybrid approach can help solve the local and global value stagnation problem in the SMO algorithm if it occurs during the process and overcome the limitations of the simulated annealing and spider monkey optimization algorithms along with a better fitness solution. The proposed algorithm's primary objective is to provide efficient resource provisioning with the optimal solution in the least time possible while increasing throughput. In addition, this proposed algorithm is compared to the PSO-SA method to demonstrate that the proposed algorithm has a more significant impact on resource provisioning.

Mathematical formulation

The proposed HSMOSA algorithm's problem and mathematical formulation for resource provisioning in the cloud environment are as follows. According to equations (2, 3, 4, 5, and 6), the local and global leaders are searched. After finding the global and local leader, applies the simulated annealing concept to search around the global best (VMs or hosts) and give maximum chance to update their position and find the optimal fitness value at each iteration. For this purpose, Eq. (7, 8) is considered.

• 3.1.    For Local Leader Search

• 3.2.    For Global Leader Search

SM nPos(i,j) = SM ij + rd(0,1) ∗ (LLpos rj - SM ij ) + rd(-1,1) ∗ (SMrd i,j - SM ij )                (2)

Where SM_ij is the SM's jth dimension. The jth dimension of the rth group's local leader is represented byLLpos_rj , SMrd_i, j represents the jth dimension of a randomly picked SM from the rth group is represented bySMrd_i, j , and rd is the range of uniformly selected random numbers.

objective function = (d + 1) ∗ xd4(De john's f4)

¹  , if ft i ≥ 0

fitfunction = fitness_i =     ^1+ft i                                                   (4)

1+absft i , if ft i < 0

Here, d is the dimension, x represents each spider, ftiis the objective function, and fitnessi is the spider monkey's fitness. This Eq. (3, 4) calculates each spider monkey's objective function and fitness (hosts or VMs) at the initial stage. After calculating the fitness value, calculate the likelihood

LSelect = 0.9 ∗

fitness i _{+ 0.1} max-fitness _i

SM nPos(i,j) = SM ij + rd(0,1) ∗ (GLpos j - SM ij ) + rd(-1,1) ∗ (SMrd rj - SM ij )              (6)

Eq. 5 is used to calculate likelihood based on the fitness value of each task. After calculating, the likelihood generates the global best by using the equation at the initial stage. 6, but for further steps after calculating the initial local and global best, eq. 5 is preferred to help search around global best.

• 3.3.    To search Around the Global Leader

3.4. Execution Time

• 3.5.    Throughput

After finding the initial local and global best value, apply simulated annealing to search around the global best at each iteration and give more chance to update their position and find the optimal fitness value.

GBestaround(GBA) = ∑ fitnessi fitnessN selection criterion = e(-∆f/GBA)(8)

ETE = ETtask - ITtask

Tput = transactions/ETE

Here Tput shows the throughput, and transactions offer the product of iterations with a total of runs for proposed HSMOSA in a cloud environment. Eq. 10 helps to calculate the throughput, which allows demonstrating whether the throughput is better or not.

• 3.6.    Mean and Standard Deviation

  deviation

  
  

  ∑ fitness max N execution

  
  

  =√

  
  

  ∑(fitness max -M) ² N execution

  
  
  
  

Here, M represents mean, fitnessmax denotes each Spider's or task's maximum fitness, Sdeviation stands for standard deviation and Nexecutionrepresents the overall execution. Eq. 11 is used to calculate the mean, and eq. 12 is used for a standard deviation of the maximum fitness value of the proposed HSMOSA algorithm.

Thus, the proposed HSMOSA algorithm's primary goal is to provide adequate resource provisioning on VMs with the shortest possible time to completion while also maximizing throughput. We suggested achieving this goal by incorporating simulated annealing approaches into the searching phase of the basic spider monkey optimization algorithm. Some of the performance indicators utilized to evaluate the effectiveness of the proposed HSMOSA algorithm are completion time, throughput, fitness value, mean, and standard deviation. Hence, the effectiveness of the proposed HSMOSA method is computed based on completion time, throughput, mean and standard deviation as represented in Eq. (9, 10, 11, and 12).

Algorithm of the proposed HSMOSA method

Algorithm 1 Algorithm for proposed hybrid HSMOSA method

• 1:    Initialize the population, the perturbation rate, the limits of the local and global leaders, the maximal

group, and the termination condition

• 2:    Evaluate position, function value, and fitness value.

• 3:    Determine who the global and local leaders seem to be.

• 4:    Local leader position update phase.

SM_(nPos(i,j))=SM_(ij )+rd(0,1)*(LLpos_rj-SM_(ij ) )+rd(-1,1)*(SMrd_(i,j)-SM_(ij ))

• 5:    Position update by global leader phase

SM_(nPos(i,j))=SM_(ij )+rd(0,1)*(GLpos_j-SM_(ij ) )+rd(-1,1)*(SMrd_rj-SM_(ij ))

• 6:    Now, applying SA on gBest and lBest value to search around the gBest and generate reduction

factor(c) and calculate the temperature

GBA= ∑ fitness_i/fitness_N

• 8:    Calculate the objective fitness value by generating a new random solution.

• 9:    ∆f=new solution-previous solution

• 10:   If the new solution< previous solution

• 11:   And if, ∆f is negative

• 12:   Then we accept the current state and increase the number of iterations; proceed to step 19.

• 13:   Otherwise, apply Selecting criterion (to accept or reject the current point)

• 14:   S=e^((-∆f/GBA))

• 15:  Make a random number.

• 16:   If random value < S

• 17:   Then accept the new point

• 18:   Otherwise, reject the new point and increase iteration (i) value.

• 19:   Check if I=i+1 is the completion of the loop.

• 20:   If not, continue to step 5.

• 21:   Update the solution

• 22:   Update the position while also checking the local and global leader limits.

• 23:   Examine the termination situation.

• 24:   If fulfilled is selected, proceed to step 26.

• 25:   Otherwise, proceed to step 2

• 26:   Obtain the output and terminate the procedure.

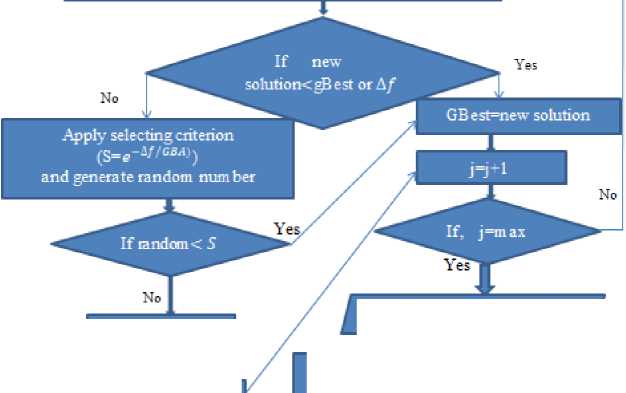
Fig. 1 depicts the proposed algorithm's flow chart representation. It shows the working of the proposed HSMOSA and how the hybridization of Spider monkey optimization with simulated annealing is implemented.

Start

Inrtialize population, perturbation rate, local leader limit, global leader limit, maximum f^oup, termination condition

Calculate function andfitness value

G enerate reduction factor, m ax. Iteration

Calculate temperature value, generate new Solution, A/1

Get the updated solution

Reject the point

GBesF=previous solution

Update the position if require and checking local lea der lim it and global lea der lim it

Fig.1. Flow chart of proposed HSMOSA method

4.    Simulation Result and Explanations

The CloudSimPlus simulator has been used to do simulations of the proposed HSMOSA algorithm. The Java programming language was required for the CloudSimPlus simulator. The performance metrics calculated during simulation are execution time, fitness value, throughput, mean, and standard deviation of the proposed HSMOSA algorithm. The performance, as mentioned earlier, indicators were calculated using varying numbers of tasks and iterations. Here, consider the 10, 50, 100, 150, and 200 no. tasks. Iterations values increase upwards from 100, 200, 400, 600, 800, and 1000. To demonstrate the feasibility of the proposed HSMOSA algorithm, compare it to the PSO-SA algorithm. Performance metrics are calculated for the proposed HSMOSA algorithm along with the PSO-SA algorithm in the context of resource provisioning. The simulation parameters required to implement the proposed HSMOSA are listed in Table 1.

The proposed HSMOSA method's performance is evaluated in seven dimensions: (i) execution time with a varying number of iterations, (ii) fitness value with a varying number of iterations, (iii) throughput with a varying number of iterations, (iv) mean and standard deviation with a varying number of iterations for task 50, (v) execution time with a varying number of tasks, (vi) fitness value with a varying number of tasks, and (vii) throughput with a varying number of tasks.

Fig. 2 shows the screenshot of the simulation result for a proposed HSMOSA algorithm on the CloudSimPlus simulator. This simulation result includes the fitness value, execution time, throughput, mean and standard deviation of the proposed HSMOSA algorithm at maximum iteration 1000 with 50 tasks.

Table 1. Simulation parameters considered in implementing the proposed HSMOSA approach

Type	Parameters	Value
Tasks	Number of tasks or size	10-200
	Number of iterations	100-1000
Broker	No. of brokers	4
Data center	No. of data centers	2
Cloudlet Length	Length of the task	10,000
VM	No. of VMs	5
	RAM	512 MB
	Size	10,000
	Operating system	Windows 10
Hosts	MIPS	1000
	Storage	10,00,000
	RAM	2048 MB
	Bandwidth	10,000

SIMULATION RESULTS

Cloudlet

DC

Host

Host PEs

VM|VM PEs

CloudletLen

CloudletPEs

FinishTime|ExecTime

ID

1 2

SUCCESS SUCCESS SUCCESS SUCCESS SUCCESS SUCCESS

ID

ID

1 2

CPU

ID I CPU

bestfitness4.396377385034731E-5

0| 0|

3|

3| summaxfit

MI

10000 10000

CPU cores

0 0

0 0

0 0

20 I

20 I

bestfitness of proposed hybrid algorithm (HSMOSA):

bestfitness4.482495853691335E-5         - bestfitness of proposed hybrid algorithm bestfitness3.4324157341937255E-5 bestfitness of proposed hybrid algorithm bestfitness3.7404151860856555E-5 bestfitness of proposed hybrid algorithm bestfitnessS.0849181328180614E-5 bestfitness of proposed hybrid algorithm bestfitness3.9889903865331685E-5 bestfitness of proposed hybrid algorithm bestfitness2.7323897480736652E-5 bestfitness of proposed hybrid algorithm bestfitness3.871916986099818E-5         ;

summaxfit i (HSMOSA):

(HSMOSA):

summaxfit

(HSMOSA):

0.0015184981200822671

4.396377385034731E-5 0.001654990733848802

4.482495853691335E-5

0.0016679303021458053

summaxfit

(HSMOSA):

3.4324157341937255E-5

0.0016009853679493312

summaxfit

(HSMOSA):

3.7404151860856555E-5

0.002198720924177914

summaxfit

i (HSMOSA): summaxfit

4.045935020698809E-6

0.0018603958006409285

summaxfit

3.9889903865331685E-5

0.0012830123016677353

bestfitness of proposed hybrid algorithm (HSMOSA):

bestfitness3.198669353548924E-5

summaxfit

bestfitness of proposed hybrid algorithm (HSMOSA):

bestfitness4.1162426936692186E-5

bestfitness of execution time probability throughput per

proposed hybrid algorithm (HSMOSA):

summaxfit

2.7323897480736652E- 5 0.0015672467418709585

3.871916986099818E-5

0.0015358939815714907

3.198669353548924E-5

0.0020169589198979153

4.1162426936692186E-5

milliseconds :2000.0

mean:2.0169589198979154E-4

standard deviation:0.0018152630279081238

• Fig.2.    Screenshot of the simulation result of the proposed HSMOSA algorithm

  Fig. 3 shows a screenshot of the PSO-SA algorithm's simulation result, including the fitness value, execution time, throughput, mean and standard deviation at maximum iteration 1000 with 50 tasks. This algorithm is implemented to show the comparison with the proposed HSMOSA algorithm.

4.824347747700767 4.460245371256502 4.052577403466136

SIMULATION RESULTS

|Cloudlet|	Status |	DC)	Host | Host	PEs |	VM	VM PEs	CloudletLen|	CloudletPEs|	StartTime|	FinishTime|	ixecTime
ID		ID)	ID|CPU	cores 1	10	CPU cores)	Hl)	CPU cores|	Seconds|	Seconds|	Seconds
:             1	SUCCESS	1)	1)	10	1	3-	10000|	3)	0	201	20
:             2	SUCCESS	1)	2)	10	2	3[	10000)	3)	0	201	20
3	SUCCESS	1)	3)	10 |	3	Я	10000)	3)	0	201	20
4	SUCCESS	1)	4)	10	4	3!	10000)	3)	0	201	20
'             0	SUCCESS|	1)	0 |	10	0	3i	10000)	3)	0	401	40
5	SUCCESS	1)	0|	10	0	4	10000)	3)	0	40)	40

Random Position :-4.288038104049395,0.7176585922241303,0.2943180285590872,-4.9981842150942954,3.074469697582578

Random Position Cost :3281.7510836945416

-2.634270802319608

-5.635065712593781

ulvaluel,0030846301160836newdesignpoint0,8467257027686426

UlvalueD.15667688033569438newdesfgnpoint0,7907822885346523 ulvalue0.7059590733354775newdesignpoint2.038220345739111 uIvaluel.3270750209694633neivdesignpoint-4.660016209559776 ulvalue0.19812313127012837newdesignpoint-1.6220973394355713

globalBest Position :-0.5312788296218985,2.8858551980437537,-0.27125348335989496,-3.7095896251961733,-3.9786424932973663. best fitness through PSOSA algorithm: 0.6561308559478736

meanl value :0.06561308659478736        standard deviation:0.5905177793530864

execution time in milliseconds :60

throughput per milliseconds :166.66666666666566

• Fig.3.    Screenshot of the simulation result of the PSO-SA algorithm

  The First performance dimension (execution time with a different number of iterations) is listed in Table 2. This shows the completion time of the proposed HSMOSA approach and the PSO-SA algorithm at various iterations. Task 50 involves the 100, 200, 400, 600, 800, and 1000 iterations. Compared to the PSO-SA algorithm, the suggested HSMOSA algorithm's execution time decreases with each iteration interval.

Table 2. The Execution time of the proposed HSMOSA algorithm along with the PSO-SA algorithm at different iterations

Number of Iteration	Meta-Heuristic Techniques
	Proposed HSMOSA’s execution time (in milliseconds)	PSO-SA’s execution time (in milliseconds)
100	6	22
200	6	30
400	5	36
600	6	45
800	6	53
1000	5	60

Fig. 4 demonstrates the graphical representation of Table 2 (the execution time of proposed HSMOSA with PSO-SA under varying iterations). This graph is generated on the CloudSimPlus simulator. The following chart shows the minimal value of execution time of the proposed HSMOSA algorithm compared to the PSO-SA algorithm while the number of iterations increases.

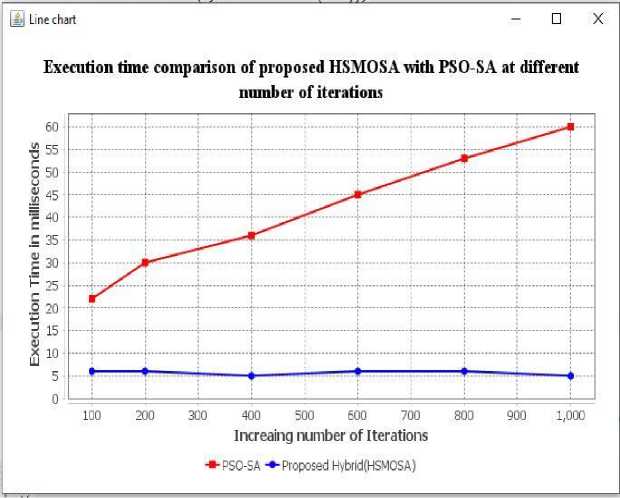
Fig.4. Execution time of the proposed HSMOSA algorithm with a different number of iterations

The second performance dimension (fitness value with various iterations) is listed in Table 3. It includes the 100, 200, 400, 600, 800, and 1000 number iterations with task 50. Fig. 5 is the graphical representation of Table 3. This graph is generated through simulation. Compared to the PSO-SA algorithm, the fitness value of the proposed HSMOSA algorithm is optimized at each iteration interval.

Table 3. The fitness value of the proposed HSMOSA algorithm along with the PSO-SA algorithm at different iterations

No. of iteration	Proposed HSMOSA's fitness value	PSO-SA's fitness value
100	0.0163	2.9165
200	0.0199	2.0893
400	0.0090	0.8015
600	0.0236	0.3338
800	0.0230	0.3894
1000	0.0225	0.6561

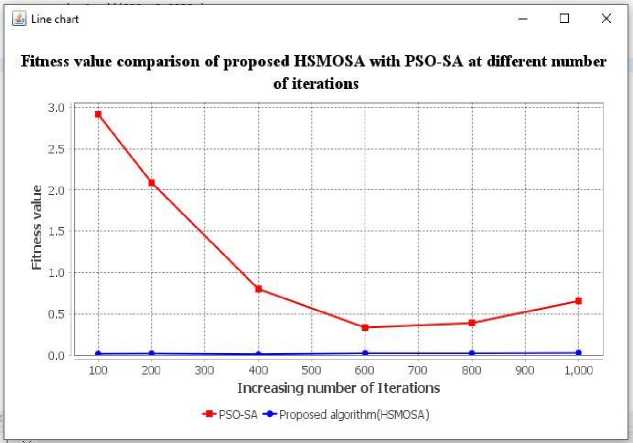
Fig.5. Fitness value of the proposed HSMOSA algorithm with a different number of iteration

The third performance dimension (throughput value with various iterations) is enlisted in Table 4. It includes the 100, 200, 400, 600, 800, and 1000 iterations with task 50. Table 4 shows that the throughput value of the proposed HSMOSA algorithm increases at each iteration interval compared to the PSO-SA algorithm. Fig. 6 demonstrates the graphical representation of Table 4. This graph is generated on the CloudSimPlus simulator.

Table 4. The throughput of the proposed HSMOSA algorithm along with the PSO-SA algorithm at different iterations

No. of iteration	Proposed HSMOSA's throughput	PSO-SA's throughput
100	166.66	45.45
200	333.33	66.66
400	800.0	111.11
600	1000.0	133.33
800	1333.33	150.94
1000	2000.0	166.66

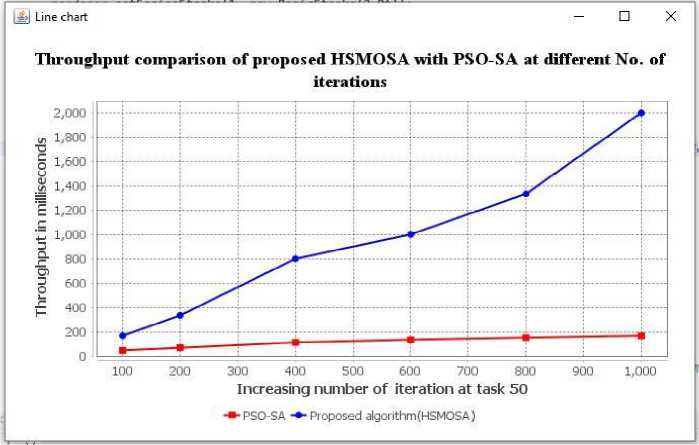
Fig.6. Throughput value of the proposed HSMOSA algorithm with different number of iteration

The fourth performance dimension (mean and standard deviation with different iterations for task 50) is listed in Table 5. It includes the 100, 200, 400, 600, 800, and 1000 iterations with task 50. It shows that the mean and standard deviation value of the proposed HSMOSA algorithm is minimized at each iteration interval compared to the PSO-SA algorithm.

Table 5. Mean and standard deviation value of proposed HSMOSA algorithm along with PSO-SA algorithm at different iterations

No. of Iteration	Proposed HSMOSA Mean value	PSO-SA Mean value	Proposed HSMOSA Standard deviation value	PSO-SA Standard deviation value
100	0.0214	0.2916	0.0010	2.6248
200	0.0238	0.2321	0.0011	2.0893
400	0.0286	0.0801	0.0014	0.7213
600	0.0311	0.0333	0.0015	0.3004
800	0.0246	0.0389	0.0012	0.3505
1000	0.0257	0.0656	0.0012	0.5905

The fifth performance dimension (execution time under a varying number of tasks at iteration 1000) is enlisted in Table 6. It includes the 10, 50, 100, 150, and 200 numbers tasks at iteration 1000. Fig. 7 demonstrates the graphical representation of Table 6. This graph is generated on CloudSimPlus simulator. As the number of tasks rises, the suggested HSMOSA algorithm's execution time decreases compared to the PSO-SA algorithm.

Table 6. The Execution time of the proposed HSMOSA algorithm along with the PSO-SA algorithm at different tasks

Number of Tasks	Meta-Heuristic Techniques
	Proposed HSMOSA’s execution time(in milliseconds)	PSOSA’s execution time(in milliseconds)
10	3	29
50	6	59
100	8	91
150	10	121
200	12	150

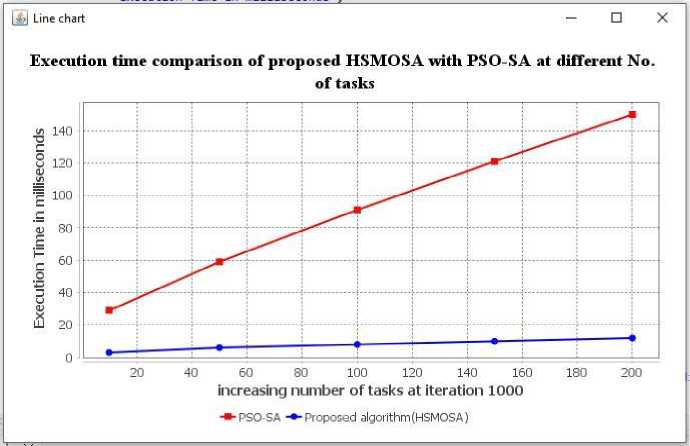
Fig.7. Execution time of the proposed HSMOSA algorithm with different numbers of tasks

The sixth performance dimension (fitness value under a varying number of tasks at iteration 1000) is mentioned in Table 7. It includes the 10, 50, 100, 150, and 200 numbers tasks at iteration 1000. Fig. 8 demonstrates the graphical representation of Table 7. This graph is generated on CloudSimPlus simulator. It demonstrates that the suggested HSMOSA algorithm has a better fitness value than the PSO-SA scheme as the number of tasks increases.

Table 7. The fitness value of the proposed HSMOSA algorithm along with the PSO-SA algorithm at different tasks

Number of Tasks	Proposed HSMOSA's fitness value	PSO-SA's fitness value
10	0.0073	0.7399
50	0.0462	0.2719
100	0.0260	0.1392
150	0.0275	0.2512
200	0.0283	0.1141

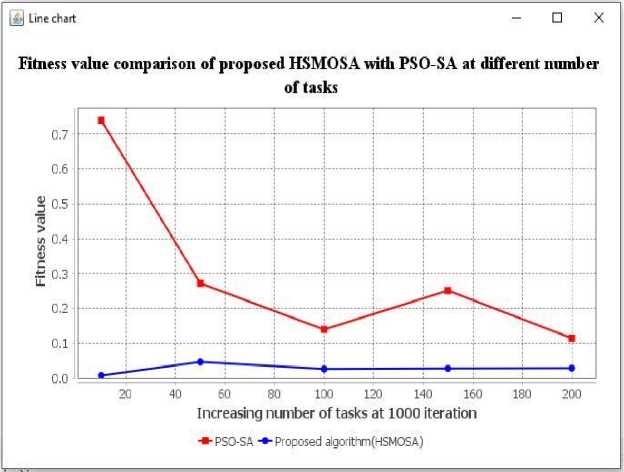
Fig.8. The fitness value of the proposed HSMOSA algorithm with different numbers of tasks

The last performance dimension (throughput value under a varying number of tasks at iteration 1000) is enlisted in Table 8. It includes the 10, 50, 100, 150, and 200 numbers tasks at iteration 1000. Fig. 9 demonstrates the graphical representation of Table 8. This graph is generated on CloudSimPlus simulator. Shows the throughput value increases of the proposed HSMOSA algorithm compared to the PSO-SA algorithm while the number of tasks increases.

Table 8. Throughput of proposed HSMOSA algorithm along with PSO-SA algorithm at different tasks

Number of Tasks	Proposed HSMOSA's throughput	PSO-SA's throughput
10	333.33	344.82
50	1666.66	169.49
100	1250.0	109.89
150	1000.0	82.64
200	833.33	66.66

|^| Line chart                                                                        —     □ X

Tliroughput comparison of proposed HSMOSA with PSO-SA at different No. of tasks

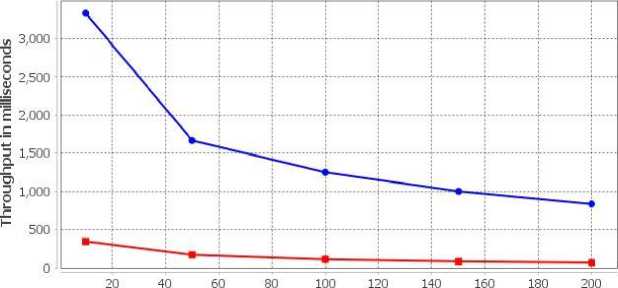
Increasing number of tasks at 1000 iteration

-•■PSO-SA -«-Proposed algorithm(HSMOSA)

Fig.9. Throughput value of the proposed HSMOSA algorithm with different numbers of tasks

5.    Conclusions and Future Scope

This research provides a solution for dealing with resource provisioning issues in the cloud environment. Hybridization of spider monkey optimization with simulated annealing is a proposed HSMOSA method. The core goal of resource provisioning is to provide resources in the shortest time possible while maintaining optimal performance. Our proposed HSMOSA method overcomes resource provisioning problems and performs well. According to simulation results, the proposed HSMOSA approach allows for resource provisioning in the minimum possible time and increases throughput. While performing resource provisioning, the execution time of the proposed HSMOSA approach is 5 milliseconds and for PSO-SA is 60 milliseconds at iteration 1000 with task size 50, the execution time of the proposed approach minimizes 55% as compared to the PSO-SA approach, which shows the better working of proposed HSMOSA method. The proposed HSMOSA approach reached 2000 while PSO-SA has 166.66 (instructions per milliseconds) at iteration 1000 with task size 50, which demonstrates that the throughput of the proposed approach is also better as compared to PSO-SA. Results show that the proposed HSMOSA method fitness value optimizes, which helps improve the position of VMs and mean and standard deviation values minimize than the PSO-SA algorithm. According to the estimated performance characteristics (execution time, fitness value, throughput, mean, and standard deviation), the proposed method has a more significant impact in the cloud environment for provisioning resources. This proposed algorithm improves SMO and simulated annealing, so it can also applicable to those areas of cloud computing where optimization of resources is require. Integration of other nature-inspired techniques with improvements regarding the performance in other different parameters like cost, energy etc for resource provisioning as future perspectives.