Hybridization of DCT and SVD in the Implementation and Performance Analysis of Video Watermarking

Today majority of the data transfer over the internet is in the form of the video and image and that is why there is a question of copyright protection and the proof of ownership comes into the picture every now and then. Both the task can be completed by a concept called digital watermarking which includes a number of techniques that are used to imperceptibly convey information by embedding it into the cover data [1]. In our paper we have taken video sequence as our cover data watermarking is thus called the Video Watermarking. The major factors that increases the demands of the Video watermarking [1, 2] are stated as below.

• •    Privacy of the digital data is required and because the copying of a video is comparatively very easy.

• •    Fighting against the “Intellectual property rights breach”

• •    Tempering of the digital video must be concealed.

• •    Copyright protection must not be eroded.

In this paper we concentrated on the two most useful and powerful mathematical transforms namely Discrete Wavelet Transform and the Singular Value Decomposition for the purpose of the video watermarking.

General idea of Implementation of the embedding and extraction of the watermark behind the video is explained in the next session. Discrete Wavelet Transform and Singular Value Decomposition are explained in the subsequent sessions. In Session 5, we explained various visual quality matrices which are used at the time of performance analysis. Session 6 explains the proposed algorithm. Last session focuses on the results and the conclusion part.

• II.    Implementation

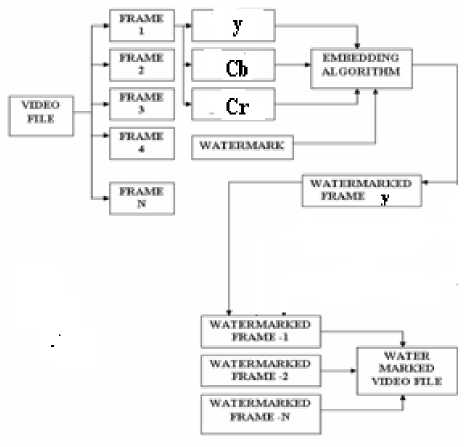
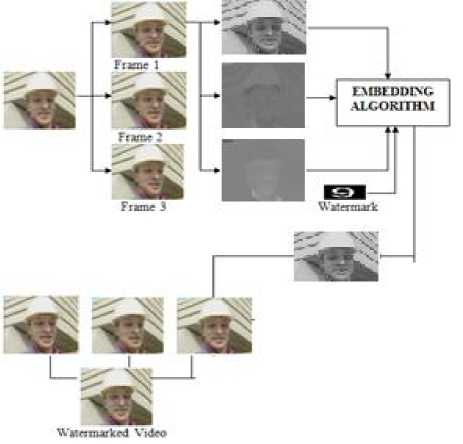
The figure 1 shows the idea of the video watermarking at the sending end. Here first of all frames is extracted from the video sequence. The next step is to perform a color space conversion from RGB to YCbCr plane and divide frames into their Y, Cb and Cr parts. Out of them the Y - luminance part is then individually given to the embedding algorithm block where the other input is a watermark to be embedded. After Y part is watermarked the next frame is taken and the procedure is repeated until the last frame.

(a)

(b)

Figure 1. Idea of Video watermarking - Embedding a watermark

III. Discrete Cosine Transform

Discrete cosine transformation [4, 5, 6] (DCT) transforms a signal from the spatial into the frequency domain by using the cosine waveform. DCT concentrates the information energy in the bands with low frequency, and therefore shows its popularity in digital watermarking techniques. The DCT allows a frame to be broken up into different frequency bands, making it much easier to embed watermarking information into the middle frequency bands of a frame. The middle frequency bands are chosen such that they have minimize to avoid the most visual important parts of the frame (low frequencies) without over-exposing themselves to removal through compression and noise attacks (high frequencies).

Two dimensional DCT of a frame with size MxN and its inverse DCT (IDCT) are defined in Equations 1 and 2, respectively.

F (u,v) =

a (u)»^)!"^  2JtoW,y)

cos

(2 x + 1) u ■ n

2 ■ M

cos

After the watermark is embedded in every frame, all frames are mixed to make the watermarked video which

(2 y + 1) v ■ n

2 ■ ^

is then transmitted in the channel.

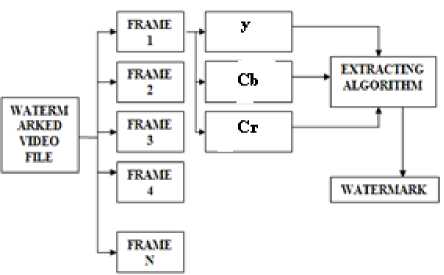
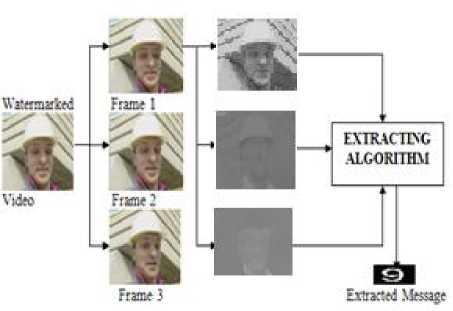
The figure 2 shows the idea of the video watermarking at the receiver end. Here watermarked video is divided into the frames. Color space conversion is performed to have y, Cb and Cr parts from which Y part is selected and the watermark is extracted. This Procedure is repeated for all frames so as to recover all watermarks.

Where a(u) = ^1/M a (u) = ^2/M a (v) = J1/N a (v) = V2/N f ⁽X,y) =

IS 2S a(u)«(r)F(u,r)

for u=0;

for u=1,2,3, for v=0;

for v=1,2,3,

.M-1;

.N-1;

cos

(2 x + 1) u ■ n 2 ■ M

cos

(2 y + 1) v ■ n 2 ■ ^

(a)

Where x = 0,1,2,……..M-1, y = 0,1,2,……..N-1

Figure 3(a) shows the three regions in the frequency domain. F L is used to denote the lowest frequency components of the block, while F H is used to denote the higher frequency components. F M is chosen as the embedding region as to provide additional resistance to lossy compression techniques, while avoiding significant modification of the cover video.

(b)

Figure 2. Idea of Video watermarking - Extracting a watermark

Fl	Fl	Fl	Fm	Fm	Fm	Fm	Fh	16	11	10	26	24	40	51	61
Ft	Ft	Fm	Fm	Fm	Fm	Fh	Fh	12	12	14	19	26	58	60	55
Fl	Fm	Fm	Fm	Fm	Fh	Fh	Fh	1J	13	16	24	40	57	69	56
Fm	Fm	Fm	Fm	Fh	Fh	Fh	Fh	14	17	22	29	51	87	80	62
Fm	Fm	Fm	Fh	Fh	Fh	Fh	Fh	1Б	22	37	56	68	109	103
Fm	Fm	Fh	Fh	Fh	Fh	Fh	Fh	24	35	55	64	81	104	113	92
Fm	Fh	Fh	Fh	Fh	Fh	Fh	Fh	49	64	7S	87	103	121	120	101
Fh	Fh	Fh	Fh	Fh	Fh	Fh	Fh	72	92	95	9S	112	100	103	99

(a)                          (b)

Figure 3. Defination of DCT regiouns and Quantization values used in JPEG compression scheme[3]

IV. Singular Value Decomposition

Singular value decomposition (SVD) [7-11] is a numerical technique based on the linear algebra and it is used to diagonalize matrices in numerical analysis. It is an algorithm developed for a variety of applications.

When we apply SVD to an Image A of size MxN, we find three matrices, namely U, V and S whose properties are:

• •    We can represent A = USV^T.

• •    U and V matrices are called Unitary matrices having size MxM and NxN respectively.

• •    S matrix is called diagonal matrix having size MxN.

• •    The columns of the U matrix are called the left singular vectors while the columns of the V matrix are called the right singular vectors of A.

• •    The diagonal entries of S are called the singular values of A and are arranged in decreasing order

• •    The singular values (SVs) of an image have very good stability, i.e., when a small perturbation is added to an image, its SVs do not change significantly;

• •    SVD [12, 13] is able to efficiently represent the intrinsic algebraic properties of an image, where singular values correspond to the brightness of the image and singular vectors reflect geometry characteristics of the image.

• •    An image matrix has many small singular values compared with the first singular value. Even ignoring these small singular values in the reconstruction of the image does not affect the quality of the reconstructed image [13].

An Example of the Singular Value decomposition is given as follows.

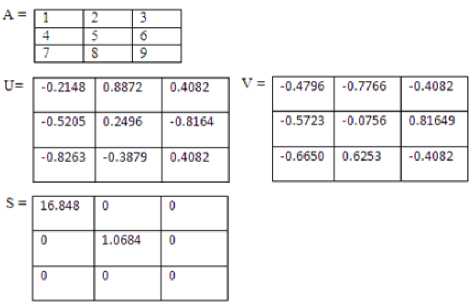
• V.    Visual quality Matrices

We have mainly used the following visual quality matrices [14] for the sake of comparison of degradation after the watermark is added to video.

M N

MSE=M1×Ν∑∑{(f(x,y)-f (x, y))^2} х=1 у=1

ΡЅΝR = 10 ×log og MSE

Here MSE – Mean Square Error

PSNR – Peak Signal to noise Ratio f(x,y) – Original Frame of the video f’(x,y) – Watermarked Frame of the Video.

The phrase peak signal-to-noise ratio

, often

abbreviated PSNR, is an engineering term for the ratio between the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of its representation. Because many signals have a very wide dynamic range, PSNR is usually expressed in terms of the logarithmic decibel scale. A higher PSNR would normally indicate that the reconstruction is of higher quality at the receiver end.

PSNR is most easily defined via the Mean Square Error (MSE) which for two m×n Frame f and f’ where one of the Frames is considered a noisy approximation of the other.

• VI.    Proposed Algorithm

In our proposed algorithm we have taken the foreman video as shown in the figure 4 and we have taken the message to be embedded as shown in the figure 5.

Figure 4. Original Video

Riya

• Figure 5. Message to be embedded

• A.  Embedding Algorithm

Following is the stepwise representation of what we have done for the video watermarking using the proposed algorithm.

• 1.    First of all the video is decomposed into the no. of frames.

• 2.    Color space conversion is performed to have Y frame.

• 3.    Divide the frame into the number of blocks.

• 4.    Read the message and apply SVD to the message.

• 5.    Take the Singular values of the SVD matrices for the embedding purpose.

• 6.    Apply DCT to the original frame and then embed the singular values obtained in the previous step in the DC part of the DCT.

• 7.    Apply Inverse DCT to obtain the watermarked frame.

• 8.    Repeat step 2 to 7 for every frame.

• 9.    Combine every watermarked frame to obtain watermarked video.

Figure 6 shows the watermarked video sequence.

Figure 6. Watermarked Video

Following Table shows the results of the proposed scheme.

T able .1 O btained PSNR and MSE values for first five frames

Frame No.	PSNR(DB)	MSE	Correlation
1	41.9171	11.9648	0.9982
2	41.9171	11.9648	0.9982
3	41.8429	12.1444	0.9974
4	41.8429	12.1444	0.9974
5	42.0171	11.5648	0.9986

• B.  Extraction Algorithm

We followed following steps to obtain the message back from the watermarked video sequence.

• 1.    First of all the video is decomposed into the no. of frames.

• 2.    Color space conversion is performed to have Y frame.

• 3.    Divide the frame into the number of blocks.

• 4.    Apply DCT to the watermarked frame.

• 5.    Obtain the singular values from the blocks.

• 6.    Apply inverse SVD to find out the watermark bits.

• 7.    Repeat steps 2 to 5 for extracting the watermarks from all the frames.

Following are the extraction results what we got from Y frame without attack.

Riya 8110

(b)

(c)

Figure 8. Watermarked Frame and messages extracted under compression attack with (a) CQ = 95 (b) CQ = 60 (c) CQ = 40

• B.  Gaussian LPF Attack

Table 3 shows the results of Gaussian LPF with a mask size of 3x3 and various sigma.

T able .3 O btained R esults under G aussian LPF attack

Riya 8110

Figure 7. Message Extracted from Y Frame without any attack

• VII.    Results

We applied various attacks on the video and found various results as discussed below.

• A.  Compression Attack

We passed the video from the jpeg compression attack and achieved results as shown in the table 2.

T able .2 O btained R esults under compression attack

Cq = 95        Cq = 60        Cq = 40

PSNR(dB)       39.0153         33.165          29.1974

MSE         27.3959         99.3629        239.1273

Correlation       0.99837          0.98957            0.681

Riya 8110

(a)

PSNR(dB) MSE

Correlation

Sigma = 0.5 34.4421 64.7254 0.96338

Sigma = 2 27.2207 333.9381 0.83254

Sigma = 3.5 27.0077 350.4674 0.8129

Figure 9. Watermarked Frame and messages extracted under gaussian LPF attack with (a) sigma = 0.5 (b) sigma = 2 (c) sigma = 3.5

C.   Gaussian Noise Attack

We added Gaussian noise with 0 mean various variances as described in the table 4.

T able .4 O btained R esults under G aussian N oise attack

	Variance = 0.0005	Variance = 0.005
PSNR(dB)	39.0153	33.165
MSE	27.3959	99.3629
Correlation	0.99837	0.98957

Variance = 0.01

29.1974

239.1273 0.681

(b)

Шуй8110

(a)

Шуй8110

Rn ii

8 И О

(c)

Figure 10. Watermarked Frame and messages extracted under gaussian noise attack with Variance (a) 0.0005 (b) 0.005 (c) 0.01

25.1839 544.5258

T able .5 O btained R esults under S alt &  P epper N oise attack

Variance = 0.005

PSNR(dB)       27.8514

MSE        288.5032

Variance = 0.009

Variance = 0.01

24.5486

626.8943

Correlation        0.9882

0.92281       0.92202

(a)

(c)

• E.    Spackle NoiseAttack

26.0079 421.7581 0.98259

We applied Spackle noise attack to the frame with various variances and taken results which appears in table 6.

T able .6 O btained R esults under S packle N oise attack

PSNR(dB) MSE

Correlation

Variance = 0.005

Variance = 0.009 23.5772 736.2925 0.93392

Variance = 0.01

23.1421

814.2854

0.88243

(a)

(b)

(c)

Figure 12. Watermarked Frame and messages extracted under spackle noise attack with Variance (a) 0.0005 (b) 0.009 (c) 0.01

RHa

• VIII.   Conclusion