Identification of handwritten complex mathematical equations

Published Online June 2019 in MECS DOI: 10.5815/ijigsp.2019.06.06

Writing in its various forms, printed and handwritten has always been an essential tool in human communication, and also omnipresent in the majority of sectors of its activities. It is used to preserve and archive knowledge. Because of this, man has always developed techniques aimed at its perpetuity throughout the generations. Indeed, with the emergence of new information technologies: electronics and computing, and the new increase in the power of machines, the automation of processing (reading, research and archiving) which are attached to it appears inescapable. It is of concern to researchers in the field of form recognition including automatic recognition of writing. This is how research in this field began over the last few decades.

The automatic recognition of writing is a complex computer process that aims to translate printed or handwritten text into a digitally encoded text, thus understandable by a machine, by transmitting to it the ability to read. The recognition of writing concerns more precisely all tasks related to the mass processing of paper documents. It therefore covers large repetitive applications with large databases such as automatic mathematics equations’ recognition, processing of administrative files, automatic sorting of postal mail, reading of amounts and bank checks, processing of postal addresses, Processing of forms, keyboard less interfaces, analysis of written gestures, reading of legacy documents, indexing of library archives and searching for information in databases.

The automatic readings of mathematical equations have seen considerable progress especially in the last decade. This is due, on the one hand, to the many works carried out leading to a variety of different approaches and, on the other hand, to the performance of computers and current acquisition systems coupled with modern statistical methods for example hidden markov models, support vector machines and neural networks. In proposed research methodology, feed forward Backpropagation neural network (BPNN) with scaled conjugate gradient and random data division has been used. The recognition rate has been determined using confusion matrix and precision, accuracy and sensitivity also been calculated.

• II.    Related Work

Optical character recognition is one of the most established thoughts in the automated pattern recognition. In recent time, recognition of mathematical equations turns into the field of useful utilization. With equation’s character acknowledgment, the procedure begins with the perusing of a scanned picture of a progression of handwritten equation, decides their meaning, and lastly makes an interpretation of the picture to a computer written equation. Likewise, different organizations and persons can utilize this technique to rapidly make an interpretation of mathematical paper reports to computer written documents.

Alvaro et al. (2013) presented a set of hybrid features that combine both on-line and off-line information. Lately, recurrent neural networks have demonstrated to obtain good results and they have outperformed hidden Markov models in several sequence learning tasks, including handwritten text recognition. Hence, this paper also presented a state-of-the-art recurrent neural network classifier and compared its performance with a classifier based on hidden Markov models. Experiments using a large public database showed that both the new proposed features and recurrent neural network classifier improved significantly the classification results [1]. Chaturvedi et al. (2014) presented a paper in which a Feed Forward Neural Network and an Izhikevich neuron model is applied for pattern recognition of Digits and Special characters. Given a set of input patterns of digits and Special characters each input pattern is transformed into an input signal. Then the Feed Forward Neural Network and Izhikevich neuron model is stimulated and firing rates are computed. After adjusting the synaptic weights and the threshold values of the neural model, input patterns will generate almost the same firing rate and will recognize the patterns. At last, a comparison between a feedforward neural network which is Artificial Neural Network model and the Izhikevich neural model which is Spiking Neural Network model is implemented in MATLAB for the handwritten pattern recognition [2]. Le et al. (2014) presented a system for recognizing online handwritten mathematical expressions (MEs) and improvement of structure analysis. It represent MEs in Context Free Grammars (CFGs) and employ the Cocke-Younger-Kasami (CYK) algorithm to parse 2D structure of on-line handwritten MEs and select the best interpretation in terms of symbol segmentation, recognition and structure analysis. This paper proposed a method to learn structural relations from training patterns without any heuristic decisions by using two SVM models. It employs stroke order to reduce the complexity of the parsing algorithm [3]. Liu et al. (2015) presented a method of mathematical formula identification in English PDF document images, which includes three steps: judging  columns,  extracting  mathematical  formula character blocks,  merging  mathematical  formula character blocks. Through analyzing and concluding characteristics of the document images in PDF files as well as its effects on mathematical formula identification, this paper designs a related parameter adjustment algorithm for avoiding influences on the performance of mathematical formula identification caused by the resolution variation. The experimental result shows that the adaptability of mathematical formula identification algorithm is improved by some applications [4]. Nguyen et al. (2015) presented application of deep learning to recognize online handwritten mathematical symbols. Recently various deep learning architectures such as Convolution neural network (CNN), Deep neural network (DNN) and Long short term memory (LSTM) RNN have been applied to fields such as computer vision, speech recognition and natural language processing where they have been shown to produce state-of-the-art results on various tasks. This paperapply max-out-based CNN and BLSTM to image patterns created from online patterns and to the original online patterns, respectively and combine them. It also compare them with traditional recognition methods which are MRF and MQDF by carrying out some experiments on CROHME database [5]. Khatri et al. (2015) presented a paper which is based on supervised learning vector quantization neural network categorized under artificial neural network. The images of digits are recognized, trained and tested. After the network is created digits are trained using training dataset vectors and testing is applied to the images of digits which are isolated to each other by segmenting the image and resizing the digit image accordingly for better accuracy [6]. Katiyar et al. (2015) presented offline handwritten character recognition of English alphabets using a three layered feed forward neural network. The proposed recognition system describes the evaluation of feed forward neural network by combining four different feature extraction approaches (box approach, diagonal distance approach, mean and gradient operations). The proposed recognition system performs well on the benchmark dataset CEDAR (Centre of Excellence for Document Analysis and Recognition) [7]. Katiyar et al. (2015) proposed an efficient Support Vector Machine based off-line handwritten character recognition system. Experiments have been performed using well known standard database acquired from CEDAR, also it proposes four different techniques of feature extraction to construct the final feature vector. Experimental results show that the performance of SVM is much better than other techniques reported in literature[8]. Chajri et al. (2016) utilized a handwritten mathematical symbols database which is characterized by the diversity of symbols writings in order to have a mathematical symbols recognition system robust and be able to know most of these symbols. This paper used four descriptors (GIST, PHOG, SURF and Centrist) and two classifiers (Artificial Neural Network (ANN) and Support Vector Machines (SVM)) for handwritten mathematical symbols recognition to achieve a comparative study based on the recognition rate [9]. Chajri et al. (2016) presented a new system able to deal with these difficulties and capable to recognize in an efficient manner these expressions. This system is based on four necessary steps: The first concerns the preprocessing techniques (Normalization, Filtering, Binarization and  Skew detection and correction). The second and third steps are respectively: the expressions segmentation (connected component algorithm) and the features extraction (Radon transform). The last step is the symbols classification (SVM). This paper also presented the results obtained by using this system (expressions segmentation, symbols recognition and the expressions recognition) [10].

• III.    System Architecture and Research Methodolgy

The system architecture for the recognition of handwritten mathematical equations have been described by using fig. 1 as shown above. The complete flow of preprocessing, segmentation and recognition has been explained.

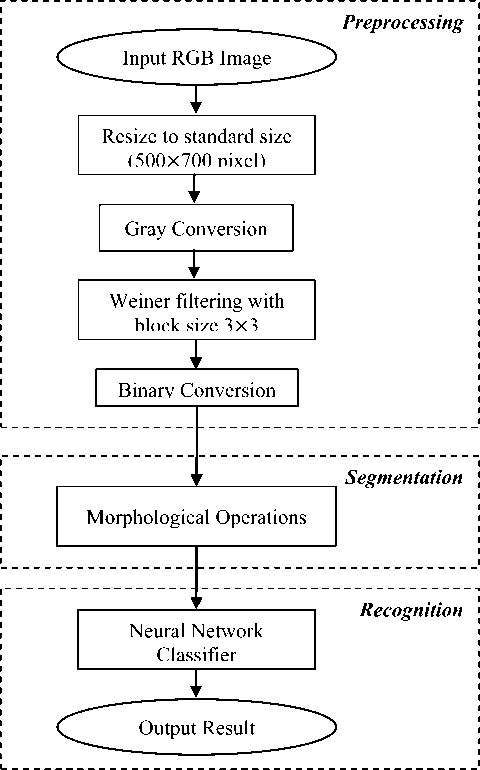
Fig.1. System Architecture for Recognition of Mathematical Equations.

• A.    Preprocessing

Generally, the scanned input image contains some irrelevant information or impurities such as holes, dirt particles and the background which must be removed. Actually the input scanned images are affected by various noises. The noise is removed using filtering. The unrelated and surplus part in the background of scanned input image has been removed.

• B.    Segmentation

Segmentation is part of the data reduction stage and involves the partitioning of the image plane into meaningful parts, such that “a correspondence is known to exist between images on the one hand and parts of the object on the other hand [11]. In binary morphology, everything could be defined using the set operations. Formally, let I and B are the sets corresponding to the image and structuring element, then

I = {(x,y) | I[x,y"] <> 0, V x,y e I r} (1)

Where I R is the set of all possible (row, column) elements over and image I. B can be defined in a similar manner. There are two basic operations in morphology, which are called dilation and erosion. The dilation of I by B is denoted by I ⊕ B and it is defined as

I ⊕ B = {c | c = i + b, where i ∈ I, b ∈ B} (2)

In the mathematics literature, the dilation is also called as Minkowski addition to refer the inventor of the operator. To complete the dilation operation, B should be translated to the every image pixel and the union of the result should be taken as an overall result. Therefore, to be precise, translation of a set should be defined to shift the structuring element to a specific image point.

The translation of set B by t is defined as follows:

Bt = {c | c = b + t, ∀b∈B}(3)

Dilation operation is defined as follows:

Dil(I,B)=I⊕B(4)

t ∈ I

In the same sense, erosion and erosion operations are defined as in below equations.

IΘB={c|c=i-b,i∈I,b∈B}(5)

Ero (I, B ) = Q10B t∈I

By using the primitive operations, several morphological operations can be defined. The two basic compound functions that could be constructed by using dilation and erosion are opening and closing respectively. The opening could be defined as dilating an image after eroding. The closing could be defined as eroding and image after dilating. As overall processes it is a smoothing operation that removes the small parasitic areas and smoothes the object contours. The opening of a set I by structuring element B is defined as:

i о b = (i e в) ® в            (6)

Similarly, the closing of a set I by structuring element B is defined as:

I • в = (I ф B) e в             (7)

Finally isolate objects in image reading line wise (left to right in each line). Resize each object to 150×100

• C.    Recognition using Neural Network Classifier

Artificial neural networks allowed us to formally simulate the work of the human brain, scientists have almost discovered how the human brain's work in terms of scalability and portability of learning memory and the ability to distinguish objects and the ability to make decisions and as we know, the brain is made up of billions of neurons interconnected in a very complex way by neuronal cells, forming an enormous network of neurons associated with them to each other. This correlation between nerve cells gives them the ability to store and deliver information, images, audio and signal sequences that receive across different neurons, neural networks also allow learning through repetition and error.

Learning MLP networks: The learning of a multilayer NN is generally done by the back-propagation approach, which is the most widely used supervised learning example for MLPs. It uses an optimization method. Universal is to find the network coefficients (weight) that minimize the global error function.

The gradient backpropagation is a method for calculating the error-gradient for every neuron in the network, from the last to the first layer, the principle of back propagation can be described in three basic steps:

Forward Propagation: Neural learning based on this algorithm uses examples of behavior. Assume the learning-base consist of N learning examples, with each comprised of x(n) vector applicable to the network inputs, and the vector d(n) of the corresponding desired values for the outputs, the vector y(n) represents the network output for the input x(n). The neural network is supposed to have ‘r′ number of output neurons. In this phase, after the initialization of the weights (w) , we calculate the input value of each neuron j of the network which is equal to the weighted sum of the output values of the neurons of the preceding layer, the formula for calculating this value is written as,

VE j = ^∑ i ∈ pred(j) W ij VA i               (8)

The output value (activation) of each neuron j(VAj) is then calculated using transfer function f, VAj = (VEj).

If we use sigmoid function as transfer function f in our work, the activation value is given by:

VA j = f(VE j ) =   ¹ -VE_j               (9)

This operation is repeated until the activation values of the output neurons are calculated.

The difference between these values and the corresponding desired values for the outputs represents the learning error called delta: (Δ) = d(n) - y(n) which must be less than a previously fixed threshold.

Back Propagation: After calculating the learning error which is the result of step of forward propagation of the inputs, in this phase will back-propagate this error through the network layers going from the outputs to the inputs (towards the back), this error will thus be distributed to the neurons of hidden layers so as to be able to adjust in the next phase the weights of the network, the computation of the error (Δ) of each neuron j of the hidden layer is made using the formula as shown below.

∆ j = VA j (1 - VA j ) ∑ k ∈ succ(j) W j K∆ k         (10)

The Update of the Weights: At the end of the previous step, the learning error was distributed (Back Propagation) to all the neurons of the hidden layers, and now in the current phase we recalculate the weights of the network which are previously initialized with random values using the following rule:

New weight = old weight + learning rate * current neuron error * output of the previous layer. This is described by the formula:

W ij = W ij + α ∗ ∆ j ∗ VA i             (11)

Where, α is the learning rate, which is usually in the range [0, 1] (chosen by the user).During the learning of the neural network, these three phases (forward propagation, back-propagation and updating of weights) are repeated as many times as the number of examples of the learning base. Once completed, the mean squared error (MSE) is computed, this measure is often applicable in binary classification where the classes are 0 and 1. This is a measure related to probabilities; it is defined by the formula:

MSE = √ ¹ ∑ k ⁿ =1 (d k - y k )²          (12)

This is a network validation step where, dk: The desired value in the learning example.

yk: The neuron value of the output layer calculated by the MLP.

The obtained MSE value must be below a certain threshold for which the model obtained can be said to respond well to the learning examples; otherwise the procedure will be repeated with other initial values of the W_i j weights and the learning rateα.

The learning phase of a neuron network can therefore be summarized by the algorithm as below.

• •    Initialization of weights with random values included in a chosen interval

• •    Reading learning examples.

• •    Normalize the training data;

• •   Repeat

• •    For each learning example D Propagation of the

entrance to the front

• •    Propagation of the error towards the back (back-propagation)

• •    Update weights

• •    End for Computation of the MSE

• •    As long as the MSE is greater than the threshold or maximum number of iterations.

• IV.    Simulation Results

The performance of proposed algorithms has been studied by means of MATLAB simulation.

Filterd Binary

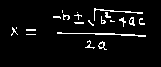
Object Detection

Input RGB Image

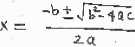
Gray Conversion

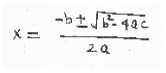
Cropped

Mask of Equation

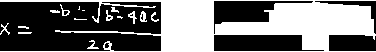
Adaptive Wiener Filtered

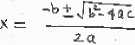
Binary Image

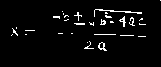
Filterd Binary

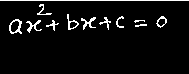
Object Detection

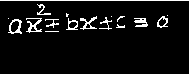
Input RGB Image

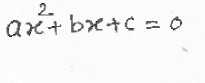
Gray Conversion

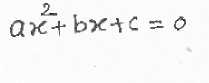
Cropped

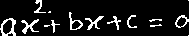
Mask of Equation

Fig.3. Operation of the second phase i.e. segmentation using morphological operations.

Matched Template

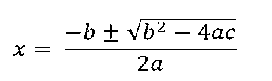
Adaptive Wiener Filtered

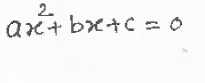
Binary Image

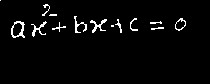
Fig.2. RGB to Gray conversion, filtering and binarization operations on input image-1

Matched Template

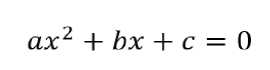
Fig.4. Matched template with input image-1

Fig. 2 shows the preprocessing steps for the proposed approach. There are four figures named as; Input RGB Image, Gray Conversion, Adaptive Wiener Filtered and Binary Image, show the respective operation on the input image.

The next operation has been explained in fig. 3 where, the required part of equation is extracted through object detection, cropping and mask of equation. Fig.4 shows the output of neural network based matching approach. It shows the matched template for the input equation image. In proposed neural network based approach there is not any threshold value for matching. Neural Network itself does the similarity measure and recognizes test image. Finally, confusion matrix plot shows the performance of proposed method.

Confusion Matrix

4 о

21 26.3%	0 0.0%	0 0.0%	0 0.0%	0 0.0%	100% 0.0%
0	4	0	0	0	100%
0.0%	5.0%	0.0%	0.0%	0.0%	0.0%
0	0	18	0	0	100%
0.0%	0.0%	22.5%	0.0%	0.0%	0.0%
0	0	0	21	0	100%
0.0%	0.0%	0.0%	26.3%	0.0%	0.0%
1	0	0	1	14	87.5%
1.3%	0.0%	0.0%	1.3%	17.5%	12.5%
95.5%	100%	100%	95.5%	100%	97.5%
4.5%	0.0%	0.0%	4.5%	0.0%	2.5%

Target Class

Fig.5. Performance evaluation through confusion matrix

The row and column are the class of handwritten mathematical equation image database. There are 5 set of classes and each class having different set of detection. For training purpose, it takes 8 images from every class and thus total 40 test images are used. The overall accuracy achieved by proposed approach is 97.5%.

Accuracy—

TP+TN

TP+TN+FP+FN

Precision- TP(14)

TP+FP

Sensitivity- TP(15)

TP+FN

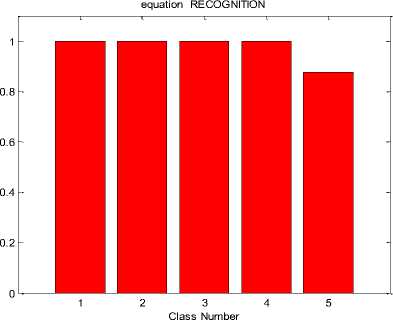
Fig.7. Precision graph for handwritten mathematical equation recognition

Where, TP — True Positive, TN — True Negative, FP —False Positive and FN —False Negative.

equation RECOGNITION

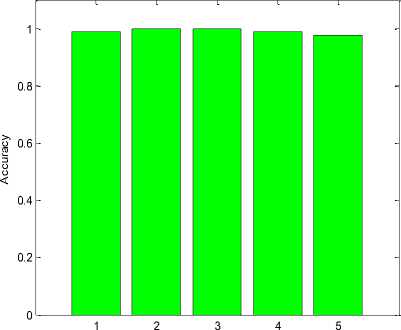
Class Number

Fig.6. Shows the bar graph of accuracy for handwritten mathematical equation recognition.

The accuracy in recognition has been described using above bar graph as shown in fig. 6 in which the recognition rate of each class number of handwritten mathematical equations have shown in fig. 6. The associated accuracy belongs to various class of equations have shown in percentage as below in Table 1.

Table 1. Accuracy for handwritten mathematical equation recognition

Class Number	Accuracy
1	0.988235294117647
2	1
3	1
4	0.988235294117647
5	0.975000000000000

Fig.7 shows the bar graph of precision for handwritten mathematical equation recognition. The performance of the system can be determined by using accuracy, precision as well. The associated precision in terms of percentage for this bar graph is shown in Table 2.

Table 2. Precision for handwritten mathematical equation recognition

Class Number	Precision
1	1
2	1
3	1
4	1
5	0.875000000000000

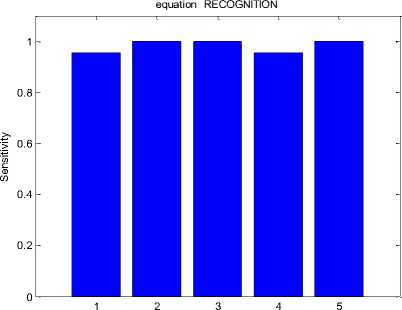
Class Number

Fig.8. Sensitivity graph for handwritten mathematical equation recognition

Fig.8 shows the bar graph of sensitivity for handwritten mathematical equation recognition. The sensitivity is main parameter to determine the efficiency as well as evaluation of the overall system. The associated sensitivity in terms of percentage for this bar graph is shown in Table 3.

Table 3. Sensitivity for handwritten mathematical equation recognition

Class Number	Sensitivity
1	0.954545454545455
2	1
3	1
4	0.954545454545455
5	1

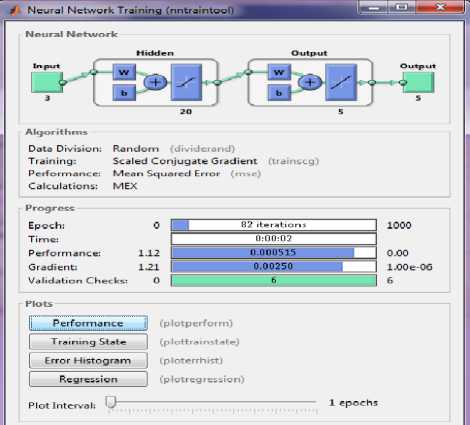
Fig.9. Neural network training

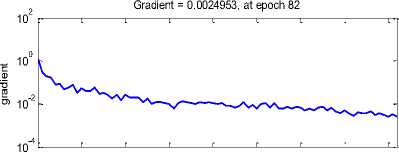
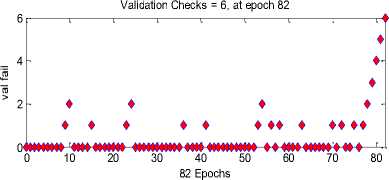
Fig.11. Neural network training state

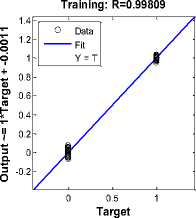
Table 4. Neural Network Parameters

Sl. No.	Parameter	Value/ Type
1	Network      Training Function	Scale Conjugate Gradient
2	Network  performance Function	Mean Squared Error ( MSE )
3	Training	R: 0.99809
4	Number of Epochs	1000
5	Number of Iteration	82
6	Performance	0.0037906 at Epoch 76
7	Gradient	0.0024953 at Epoch 82
8	Calculations	MEX

Error Histogram with 20 Bins

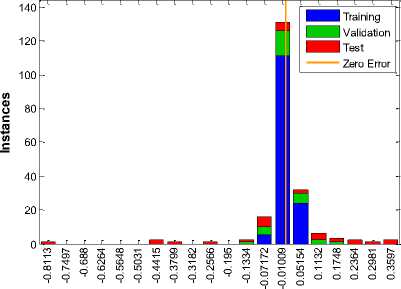
Errors = Targets - Outputs

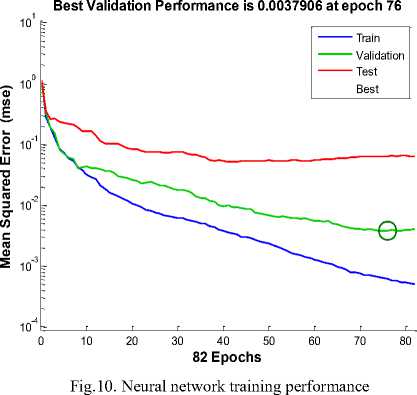
Fig.12. Neural network training error histogram

Target

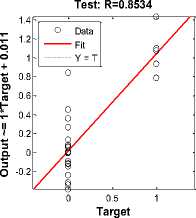
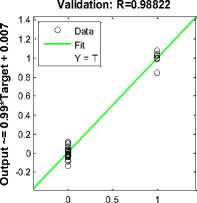
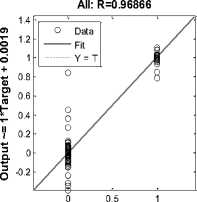
Fig.13. Neural network regression

Target

The neural network is formed with three input nodes, twenty hidden nodes and three output nodes. The data division is random and network has trained with scaled conjugate gradient and the performance of the network has measured using mean squared error as shown in fig. 9. The performance and efficiency of the neural network can also be observed by using training performance, training state, error histogram through error by subtracting output from target and network regression as shown in fig. 10, fig.11, fig.12, and fig, 13 respectively.

• V.    Conclusions

This paper addressed the steps necessary to build a system of handwritten mathematical equation recognition based on morphological operations and neural network matching with scale conjugate gradient for training the network. Simulation results show that the proposed approach successfully recognized the mathematical equation from the given database. In preprocessing approach RGB to gray conversion is used along with resizing. Weiner filtering is used to remove the noise in the image. Main contribution is the study of the implementation of the morphological operation for the segmentation process and finally the neural network base matching provides the recognition accuracy of 97.5%. The performance of the classifier has measured using the error histogram and confusion matrix based on accuracy, precision and sensitivity.