Идентификация динамической системы процесса уплотнения асфальтобетонной смеси дорожными катками

В дорожном строительстве широкое распространение получили вибрационные катки. Рабочий процесс вибрационного катка направлен на достижение требуемой плотности асфальтобетонного покрытия за счет многократных воздействий вальцом (вальцами) на уплотняемый материал с повторяющимися проходами. Уплотняемая среда – асфальтобетонная смесь, характеризуется существенной нелинейностью из-за непрерывного изменения характеристик при деформации нелинейной упруговязкопластической среды, изменения температуры уплотняемого слоя во времени, процесса релаксации напряжений, температурной сегрегации и других факторов, что требует постоянного внимания со стороны оператора за управлением режимами работы вибрационного катка. Обеспечение эффективной работы дорожных катков возможно только за счет автоматизации технологических процессов.

Зарубежные производители вибрационных катков предлагают автоматические системы управления (АСУ) процессом уплотнения (Asphalt Manager фирмы Bomag), контрольно

измерительные системы (АСЕ – Ammann Compaction Expert компании AMMANN) и другие АСУ, адаптированные к своим типам вибрационных катков. Эти и другие аналогичные системы позволяют осуществлять непрерывный контроль за степенью уплотнения (коэффициентом уплотнения), настраивать амплитуду и частоту колебаний вальца в зависимости от скорости дорожного катка и температуры поверхности асфальтобетона. Результаты работы дорожных катков с современными АСУ не гарантируют получение качественных асфальтобетонных покрытий – брак составляет до 65 % [1]. Основные проблемы: отсутствие автоматизации управления при реверсировании, плавности перехода с одной полосы на другую; учет изменения температуры при управлении процессами.

Производство дорожных катков предприятиями Российской Федерации растет. Автоматические системы управления процессом уплотнения на современные дорожные катки отечественного производства не устанавливаются. Необходимость выполнения научной работы по совершенствованию конструкций и разработке систем управления вибрационных катков определяется наличием нерешенных научно-исследовательских задач теории рабочего процесса уплотнения среды, а также наличием современных проблем обеспечения качества до -рожных покрытий.

Целью научной работы является: разработка имитационной динамической модели процесса уплотнения асфальтобетонной смеси вибрационным катком, проверка её адекватности, проведение численного эксперимента и обработка полученных экспериментальных данных.

Имитационная динамическая модель процесса уплотнения

Основными показателями, характеризующими напряженно-деформированное состояние асфальтобетонной смеси в процессе уплотнения, как нелинейной упруго-вязко-пластической среды, являются контактное напряжение и величина деформации. Широкое распространение для теоретического описания уплотняемой среды у российских [2] и зарубежных [3] ученых получили методы реологии. Существующие реологические модели не нашли широкого практического применения при разработке систем управления из-за отсутствия доступных специалистам выходных реологических характеристик этих моделей, которые можно получить в результате экспериментальных исследований.

Для решения поставленной задачи в качестве базовой принята теория уплотнения, предложенная в работе [2]. С учетом конструктивных элементов катка схема модели процесса вибрационного уплотнения асфальтобетонной смеси приведена на рис. 1.

ПРИТРИ

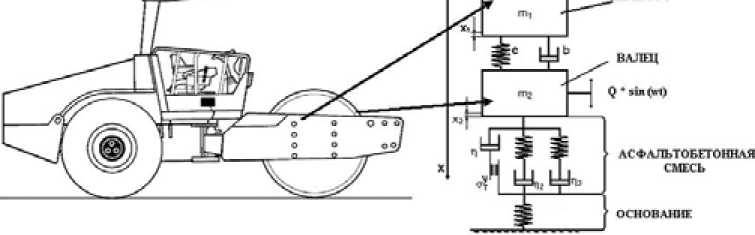
Рис. 1. Модель процесса вибрационного уплотнения асфальтобетонной смеси дорожным катком

Модель условно можно разделить на две части: первая описывает динамику колебаний вибрационного вальца, вторая – реологические свойства уплотняемой среды.

Дифференциальные уравнения колебательной системы можно записать следующим образом [1]:

”1-

<

d ² x , ( t ) dt²

+ b

r.

dx O) ¹ dt V

)

dx ₂( t )       / , x

^- л   ⁺ c ^{( x (} t ¹

- x ₂ ⁽ t ) ) = m ■ g ;

)

d ² x ₉ ( t ) / dx i ( t ) dx^ ( t ) )

m2--"Л--bl ~,---^ | - c (x1 (t) - x2 (t)) = Q ■ Sm(® t) + m2 ■ g - P(tX dt V dt dt )

где m2 - масса вальца, которому сообщаются гармонические колебания от вибровозбудителя, кг; т 1 - масса пригруза (масса рамы вальца, воздействующая на вибрирующий валец), кг; х 1 - вертикальное перемещение корпуса катка, возникающее от вращения дебалансного вала вальца и передающееся через резиновые амортизаторы, м; х2 - вертикальное перемещение вибрационного вальца, м; b – коэффициент вязкого трения резиновых амортизаторов, Па*с/м; с – жесткость резиновых амортизаторов, Н/м; Q – вынужда ющая сила вибровозбудителя, Н; ω – угловая частота вращения вала вибровозбудителя, рад/с; t – текущее время вибрационного воздействия на смесь, с; P(t) – реакция на валец со стороны уплотняемой смеси, Н.

Для удобства проведения компьютерного имитационного моделирования уравнения, полученные в работе [2], были преобразованы, что позволило более детально исследовать динамические процессы. После преобразования система уравнений (1) имеет следующий вид:

^{d е(} t ) =____ ⁽ m i ⁺ m 2 ) ' g ____₊_________ Q ___{sm(m t} )

dt ²       ( 0,02 . m , ⁺ m 2 ) • h сл ( t )   ( 0,02 . m , + m 2 ) . h сл ( t )

- .------ L AB ⁽ t ) • B ----• ^ ( t ) ;

( ^0,02 • m , ⁺ m 2 ) • h сл ( t )

d²c_fc ( t ) = 6₂ • n + 0 3 • m da_k ( t )   [ ^CT k ⁽ t ) ^- ^ T ]

dt²           0₂ • 0₃ • n • m dt 0₂ • 0₃ • n • m

П 2 + П з      ^{d e} ( t ). П 2 • 0 з + П з • 0 2 ^d2 ^е ( t )

----1-----—

0 ₂ . 0 ₃ . n . m dt       0 ₂ . 0 ₃ . n . m dt ²

где В - ширина вальца, м; h_сл( ) - толщина слоя смеси, м; L AB ( t ) - длина дуги контакта вальца со смесью, м; 9 2 , 9 3 - время быстрой и медленной релаксации напряжений, соответственно, с; n, m - коэффициенты, постоянно изменяющиеся в процессе уплотнения; п₂, П 3 - вязкость смеси в блоках 2 и 3 реологической модели смеси соответственно, Па*с.

С учетом принятых упрощений система уравнений (2) преобразована:

d 2s( t)

dt 2 = a 0 ⁺ b 0 • ^sin ( ® t ’ ^— c 0 • ⁿ ( t ) ;

<

d ^ ( t ) = dt^г

—

„ d ^CT k ⁽ t ’    „ Г.,. _(Л уУ                  ^{d s(} t )

■ ci —;--c21 ^k(t’— ^t l + c2(n2 + пз’—;— + dt                                    dt

d2s(t)

⁺ c 2^(П- ' ® - ^{+ П}> ' ’ 2’•

(m + m7 )• g ,Q где a0 =      12       ; b0 =

⁽ 0,⁰² • m i + m 2 ) • h сл ⁽ t )        ^{( 0},02 • m i + m 2 ) ■ h сл ⁽ t )

c =       LAB(t)' B       . c = 62 ■ n + 63 ■ m . c =

.

⁰     ( 0,02 ■ m i + m 2 ) ■ h сл ( t )’ ¹     6 2 ■ 6 3 ■ n ■ m’ 2 6 2 ■ 6 3 ■ n ■ m

В модели присутствуют две подсистемы SubSystem и SubSystem1 (рис. 3, 4). Задающим сигналом является угловая частота вращения дебалансного вала, которая определяется по формуле to = 2 n • f,

где f – частота вибрации вальца, Гц. В данной задаче исходная частота f =50 Гц.

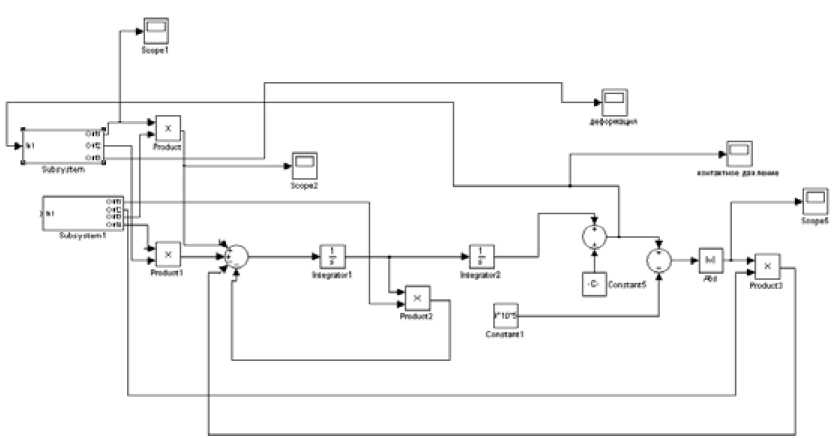
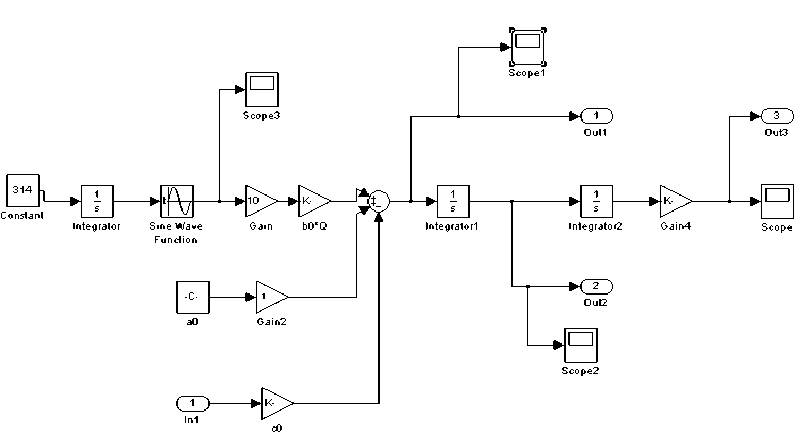
Рис. 3. Содержание блока SubSystem

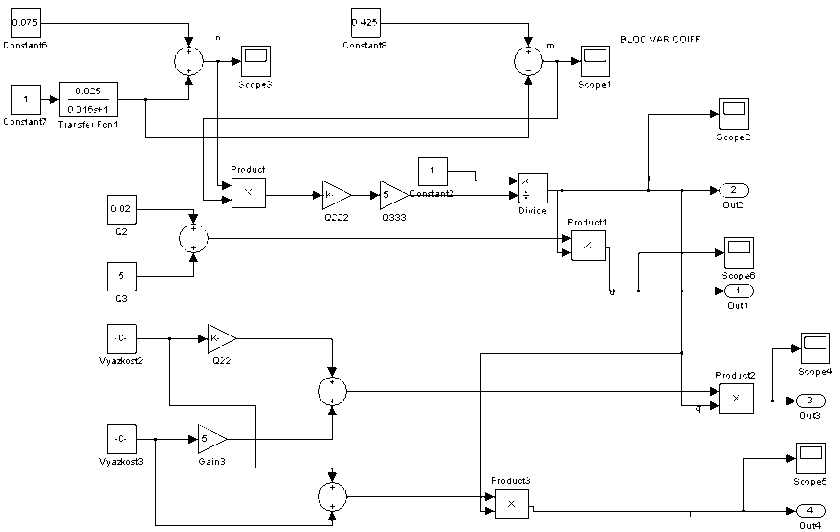
Рис. 4. Содержание блока SubSystem1

Входом In1 подсистемы SubSystem является величина контактного давления, выраженная из второго уравнения системы (2), а её выходом – величина деформации среды.

В подсистеме SubSystem1 реализован учет свойств вязкости среды, выходами подсистемы служат данные для построения модели уравнения (3).

Свойства вязкости среды, нелинейно изменяющиеся в процессе уплотнения, учитываются при помощи коэффициентов m и n . Модели и зависимости изменения этих коэффициентов от времени приведены на рис. 5 и 6.

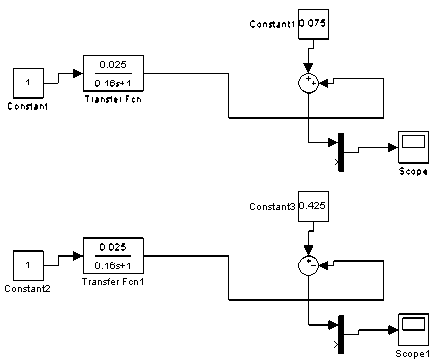
Рис. 5. Модель изменения коэффициентов m и n от времени

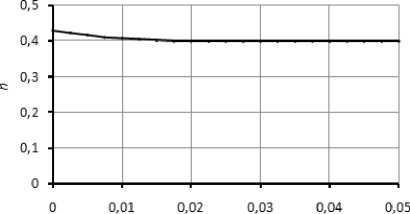
t,c

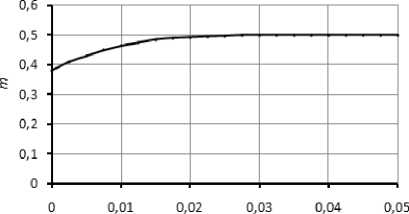
t,c

Рис. 6. Зависимости изменения коэффициентов n и m от времени

Результаты исследования

Исходные данные к модели процесса уплотнения асфальтобетонной смеси дорожным катком:

Q – вынужденная сила вибровозбуждения, 45*10³ Н;

B – ширина вибрационного вальца, 1,5 м;

m 1 – масса пригруза (рамы), 3,5*10³ кг;

m 2 – масса вибрационного вальца, 2*10³ кг;

θ 2 – время релаксации в блоке 2 реологической модели смеси, 0,02 с;

θ3 – время релаксации в блоке 3 реологической модели смеси, 5 с;

σ m – предел текучести, 0,9 МПа;

η 2 – вязкость смеси в блоке 2 реологической модели смеси, 0,35 МПа*с;

η – вязкость смеси в блоке 3 реологической модели смеси, 0,35 МПа*с; 3

n0= 0,075, nк = 0,1, m0= 0,425, mк= 0,4 – коэффициенты распределения контактного давления;

V m – скорость движения катка, 0,55 м/с;

h cл – толщина слоя смеси, 0,06 м; ρ 0 – начальная плотность смеси, 0,94 кг/м³.

Адекватность имитационной модели проверена по результатам моделирования динамики рабочего процесса уплотнения асфальтобетонной смеси вибрационным катком. Получены зависимости контактного давления вальца и абсолютной деформации смеси от времени контакта вальца с уплотняемой смесью, а также ускорение изменения деформации уплотняемой среды (рис. 7 – 9).

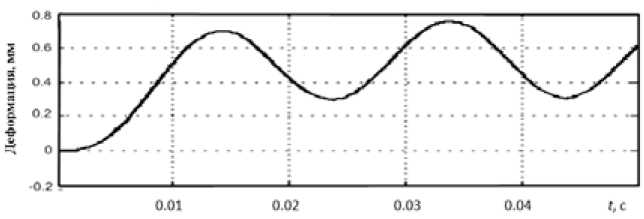
Рис. 7. Зависимость абсолютной деформации смеси от времени контакта вальца с уплотняемой смесью

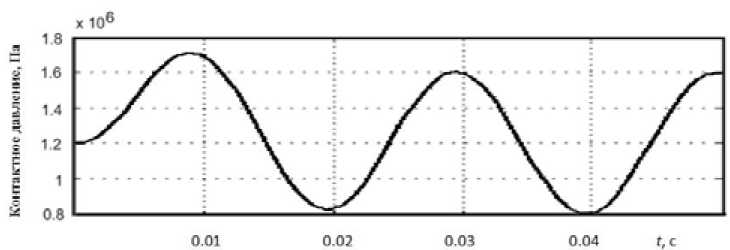
Рис. 8. Зависимость контактного давления вальца от времени контакта вальца с уплотняемой смесью

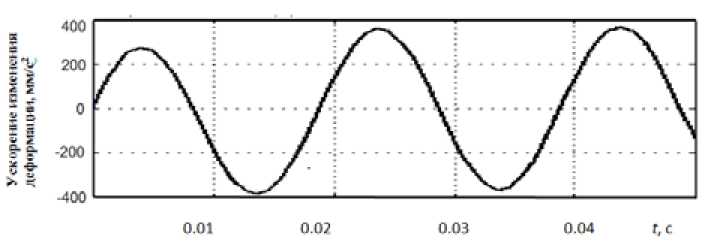
Рис. 9. Зависимость ускорения изменения деформации смеси от времени контакта вальца с уплотняемой смесью

Выполнена обработка результатов исследования методом планирования эксперимента [4]. Для анализа результатов были выбраны следующие параметры, влияющие на реологические свойства уплотняемой среды и динамику вибрационных свойств вальца, а также диапазоны изменения этих параметров:

• -    время быстрой 0₂ и медленной 9 3 релаксации напряжений, изменяющиеся в диапазонах: 0 2 = 0,005.. .0,05 с, 9 з = 0,5.. .10 с;

• -    вязкость смеси в блоках реологической модели: п ₂, П 3 (0,1. ■ .0,6 МПа*с);

• –    частота вибрации f (40…50 Гц).

Используя опытные данные и указанные факторы, рассчитали коэффициенты регрессионных моделей и показатели достоверности аппроксимации.

Погрешности вычислений составили:

• •    для контактного давления 0,1 %;

• •    для деформации 8 %;

• •    для ускоре ния изменения деформации 0,6 %.

С использованием программы MS Excel получены уравнения регрессии, отражающие влияние каждого исследуемого фактора на один из трех откликов: контактное давление вальца, деформацию смеси и ускорение изменения деформации смеси (рис. 10 – 13).

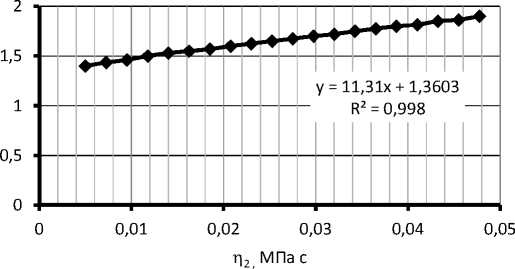
Рис. 10. Зависи мость контактного давления вальца от вязкости в блоке 2 реологической модели смеси

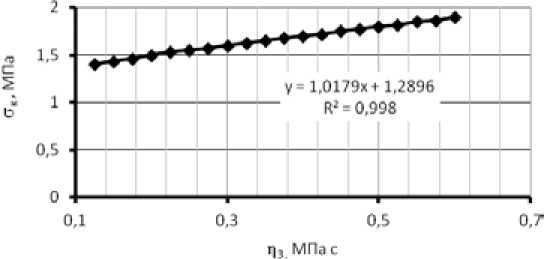
Рис. 11. Зависимость контактного давления вальца от вязкости в блоке 3 реологической модели смеси

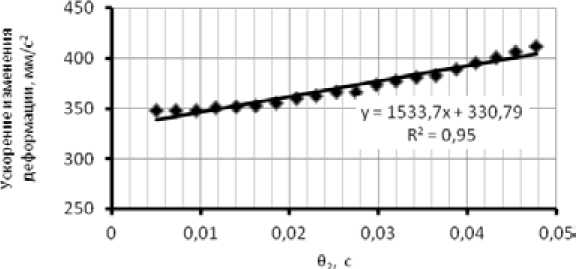
Р ис. 12. Зависимость ускорения изменения деформации смеси от времени релаксации в блоке 2 реологической модели смеси

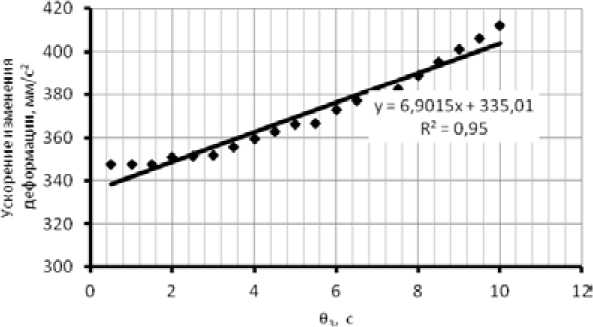
Рис. 13. Зависимость ускорения изменения деформации смеси от времени релаксации в блоке 3 реологической модели смеси

Выводы

Разработана имитационная динамическая модель процесса уплотнения асфальтобетонной смеси вибрационным катком, позволяющая упростить исследование динамических процессов, вызванных изменением параметров дорожного катка и уплотняемой среды при проведении численных экспериментов.

Результаты работы могут использоваться для идентификации параметров среды и параметров вибрации при разработке системы автоматического управления процессом уплотнения, в частности для выбора соответствующих датчиков контактного давления, деформации, ускорения изменения деформации.