Идентификация функции активности пользователей социальной сети в линейной диффузионной модели

Original Empirical Research

Identification of the Activity Function of Social Network Users in a Linear Diffusion Model

Margarita A. Tolstykh © H , Victor K. Tolstykh ©

Donetsk State University, Donetsk, Donetsk People's Republic

Introduction . Improving the accuracy of mathematical models for disseminating information in social networks is directly related to the ability to correctly identify their parameters. In numerous papers, the fundamental complexity of this problem is actually bypassed by substituting the direct identification of the desired functions for the selection of parameters for their heuristic approximations, which inevitably leads to a decrease in both the accuracy and universality of the model. In the linear diffusion model describing the spatiotemporal dynamics of information, one of the key parameters is the function characterizing user activity. The objective of this study includes the development and numerical implementation of an algorithm for direct parametric identification of user activity functions based on a direct extreme approach, which makes it possible to completely abandon heuristic approximations, and the evaluation of its computational efficiency in comparison to the classical gradient method.

Materials and Methods. A direct extreme approach was used to solve the parametric identification problem. Unlike the classical steepest descent technique, the proposed method with adjustable descent direction adapted the search trajectory to local features of the quality functional through introducing a control parameter. The numerical solution to the direct and adjoint problems was implemented using an implicit finite-difference scheme. The method was verified using synthetic data.

Results . For the identification algorithm, an analytical expression of the gradient of the target functional was obtained through the solution to the adjoint problem. The identifiability limits of the desired parameter conditioned by the inertia of the diffusion process and the network response time were determined. A comparative study of gradient algorithms was conducted. The classical steepest descent approach demonstrated slow and uneven convergence, requiring 13,217 iterations to reach the stopping criterion, whereas the method with adjustable descent direction provided convergence to the same level of accuracy in 376 iterations.

Discussion. The obtained results confirm the theoretical assumptions about the need to take into account the spatial heterogeneity of the functional gradient when solving infinite-dimensional optimization problems. The classical gradient technique exhibits low efficiency in reconstructing nonstationary parameters due to gradient nonuniformity, while the method with adjustable descent direction reaches uniform and rapid convergence. This demonstrates that adapting the algorithm to the specifics of an infinite-dimensional problem is a key success factor. The main contribution of the research is the development of a computing apparatus for the direct determination of functional parameters, which expands the methodological arsenal for analyzing systems described by partial differential equations.

Conclusion. The key findings of this research are the development and verification of an efficient algorithm for direct identifying user activity functions in a linear diffusion model of a social network. The practical significance consists in the creation of more accurate and interpretable tools for modeling information flows without resorting to a priori approximations. The developed algorithm has demonstrated significant advantages in speed and convergence. However, the interpretation of the physical meaning of the identified function within this model requires further development. A promising direction is the application of the method to more sophisticated models that take into account the spatial heterogeneity of user activity, as well as its extension to the identification of the function vector.

Acknowledgements . The authors would like to thank the research team of the Department of Computer Technologies, Donetsk State University, for fruitful discussions of the research materials.

Funding Information. The work is done with the financial support from the Azov-Black Sea Mathematics Center for conducting fundamental scientific research (Agreement No. 075-02-2025-1608 dated February 27, 2025).

Введение. Социальные сети стали неотъемлемым элементом современного общества, осуществляя не только развлекательную функцию, но и выступая инструментом формирования общественного мнения и среды для создания различных сообществ, объединенных интересами (бытовыми, политическими, экстремистскими и т.д.). В связи с этим задачи изучения, прогнозирования и регулирования распространения информации, а также выделения и классификации сообществ в социальных сетях приобретают повышенную актуальность. Решение указанных задач требует разработки точных математических моделей таких процессов.

Существует большое разнообразие социальных платформ, каждая из которых отличается собственной структурой и механизмами передачи информации. Постоянная эволюция и появление новых алгоритмов функционирования социальных сетей приводят к значительному разнообразию их математических моделей. Эпидемические модели SI, SIR, SEIR [1] и их современные усложненные версии в виде моделей среднего поля [2] классифицируют узлы (пользователей) в социальной сети по состояниям и описывают количественное изменение узлов определенного класса. В то же время графовые модели в виде линейной пороговой и каскадной [3] акцентируют внимание на кумулятивном эффекте распространения информации и зачастую используются для поиска лидеров мнений в социальной сети. Каждая из упомянутых моделей описывает лишь частные аспекты распространения информации, не охватывая этот процесс в его пространственно-временной полноте.

В последние годы широкой популярностью стали пользоваться модели на основе машинного обучения, способные с высокой точностью прогнозировать динамику распространения информации [4] . Однако подобные модели, как правило, функционируют по принципу «чёрного ящика» и не предоставляют интерпретируемых параметров (например, виральности, пропускной способности сети или активности пользователей). Отсутствие таких параметров ограничивает возможности исследователей в оценке кластеров социальной сети и управлении процессами распространения информации, что ставит под угрозу применение моделей в задачах, требующих понимания внутренних механизмов диффузии.

Информатика, вычислительная техника и управление

В работах [5, 6] отмечается целесообразность построения принципиально общей модели, не привязанной к постоянно изменяющимся алгоритмам функционирования социальных сетей. В исследовании [7] с целью достижения этой цели предлагается использование математического аппарата уравнений в частных производных, а именно — линейной диффузионной модели:

д v д t

д2 v x,t e Q = (Xa,Хь)x(tо,ti),

p—- - rhv = 0 , дx ²

где t — время; x — расстояние в графе сети, измеряемое минимальным количеством рёбер, по которым может быть передана информация V ( x , t ) ∈ L 2 (Ω) (например, в виде количества репостов определенной новости); L 2 — евклидово пространство функций с интегрируемым квадратом.

Авторы определяют параметры модели следующим образом: p — популярность информации (виральность, скорость диффузии информации в сети); h — пропускная способность социальной сети (максимальное количество пользователей, которые могут принять участие в распространении информации); r — активность пользователей (скорость роста информации в сети).

Модель (1) учитывает пространственно-временные закономерности распространения информации, а её параметры могут быть настроены для отражения особенностей конкретных социальных сетей [7] . Ключевой проблемой в данном случае становится задача параметрической идентификации модели. В общем случае все указанные параметры должны быть функциями: p ( x ) , h ( x ) , r ( t ) . Авторы модели (1) предлагают аппроксимировать эти функции различными эвристическими зависимостями, что приводит к задаче параметрической идентификации набора коэффициентов-чисел, входящих в эти зависимости [8, 9] . Такое упрощение не позволяет достичь максимальной точности, которая возможна только при идентификации непосредственно указанных функций, а не их аппроксимаций, поскольку для разных социальных сетей и даже кластеров одной социальной сети может существенно различаться набор входящих в модель параметров. Авторы работы [10] справедливо указывают, что аналитически найти оптимальные параметры-функции зачастую невозможно, и классические численные методы оказываются неэффективными.

В работе [11] рассматривается задача прямой идентификации функции h ( x ) . Для поиска её оптимального значения применяется прямой экстремальный подход [12] , основывающийся на непосредственной минимизации критерия качества идентификации J ( h ) экстремальными алгоритмами градиентом V J ( h ; x ). Хотя в работе [11] была сделана попытка прямой идентификации h ( x ), задача идентификации временной функции r ( t ) для подобных моделей в литературе систематически не исследована. Целью настоящей работы является восполнение указанного пробела путём разработки и численной реализации алгоритма прямой параметрической идентификации функции активности пользователей в линейной диффузионной модели (1) на основе прямого экстремального подхода. Основная задача заключается в оценке эффективности градиентных алгоритмов для достижения данной цели. Решение этой задачи создаст методологическую основу для последующей идентификации других параметров (например, p ( x ) или одновременной идентификации вектора параметров-функций) и перехода к более сложным нелинейным моделям. Параметры h ( x ) и p ( x ) в рамках данной работы считаются известными и взяты из работы [5] для изоляции и детального анализа целевой задачи.

Материалы и методы. Для моделирования процессов распространения информации по уравнению (1) в исследуемом кластере графа сети были заданы граничные условия первого и второго рода:

дv v = 1 на Г a = xa х( t0 ,t 1), — = 0 на Г b = xb х( t0 ,t 1).

Здесь предполагается, что источник информации находится в узле x_a и в момент времени t = t ₀ генерирует информацию v ( x_a , 1 ₀) в виде одной новости. Значение x b определяет расстояние, на котором поток информации исчезает.

Начальное условие соответствует отсутствию обсуждаемой новости в сети:

v = 0 на Г 0 = ( x_a ,x_b ] х 1 0 .

Критерий качества идентификации модели был задан в виде отклонения модельного состояния v от экспери- ментально наблюдаемого ve в реальной сети на всей пространственно-временной области Q в виде следующего функционала:

J(r HL(v

- v e ) ² dxdt.

Задача параметрической идентификации оптимального значения функции r *( t) формулируется как экстре- мальная задача:

r = arg min J ( r ) .

r e L 2 ( S ) ^{V 7}

Для решения данной задачи использовался бесконечномерный градиентный алгоритм:

r k ^{+ 1} ( t ) = r k ( t ) - b k a ( t ) V J ( r k ;t ) , t e S _д c S, k = 0 , 1 ,..., (3) где k — номер итерации; b k — шаговый множитель (выбирался методом золотого сечения); a ( t ) — параметр регулирования направления спуска. Если a ( t ) = 1, то алгоритм (3) сводится к классическому методу наискорейшего спуска (МНС). В противном случае данный алгоритм представляет собой метод с регулируемым направлением спуска (MPHC) [12] . Параметр a ( t ) выполняет регулировку направления спуска к оптимуму для обеспечения равномерной сходимости функций r^{k +1}( t ) к r*. ( t ) на S _д с S , где в принципе возможна равномерная сходимость. Для МРНС, согласно [12] , параметр регулирования направления спуска можно задать:

a ( t ) =

r ⁰ ( t )

I^V J ( r ⁰ ;t )Г

Для реализации алгоритма (3) необходимо нахождение аналитического выражения градиента целевого функционала (2), зависящего от управления неявно, что является основной сложностью при бесконечномерной иден- тификации. Градиент находится через решение сопряженной задачи, техника получения которой широко описана в литературе [13, 14].

Для оценки эффективности решения задачи параметрической идентификации функции активности пользователей в модели (1) посредством прямого экстремального подхода (3) была поставлена следующая тестовая задача.

Исходное и сопряженное линейные параболические уравнения решались численно по неявной конечно-разностной схеме Кранка-Николсона методом прогонки. Пространственно-временная сетка задавалась значениями n = 50, m = 500. Это соответствовало расстоянию в пять рёбер графа сети на которое распространилась новость от источника, и времени t 1 – t 0 = 72 часа. Было принято t Δ = 5 часов.

Для построения синтетических данных v e параметры p и h считались известными и были взяты из работы [5] : p ( x ) = e ~ x , h ( x ) = - 0 , 03 x ² + 0 , 2 x.

Задавалось тестовое оптимальное значение, которое также предлагалось в работе [5] :

r * ( t ) =

0 , 0059 - e -i , ₅₅ 26 1 f 0 , 0059 - 1]

1, 5526            1 1 , 5526    ) ^.

Решалась прямая задача для модели (1). Полученное состояние v ( x , t ) принималось как «экспериментальное» v e ( x , t ). Далее задавалось начальное приближение r ⁰( t ) = 0,3 и начинался итерационный процесс решения обратной задачи идентификации экстремальным алгоритмом (3) для восстановления функции r_* ( t ).

Условием остановки итераций был следующий критерий практического прекращения сходимости:

k - u k ^{- 1}

k - 1

< 10 ^{- 5} .

Результаты исследования. Для алгоритма (3) был найден градиент:

x b

V J ( r;t ) = -    hvfdx e L ₂ ( S _д ) .

xa

Он определяется через решение следующей сопряжённой задачи f :

-

f d t

-

52 f p ~—p - frh + 2 (v - ve ) = 0, x,t e Q,

с соответствующими граничными и начальным (терминальным) условиями:

df pf = 0 на Г a, p— = 0 на Г b, f = 0 на Г1 = [ xa ,xb lx 11.

d x

Сопряжённая задача решается в обратном по времени направлении от начального нулевого состояния f на Г 1 . При неоптимальном значении r ( t ), через некоторое время t Δ за счёт свободного члена 2( v – v e ) в уравнении (5) формируется ненулевое состояние f . Если провести анализ управляемости, то получим множество управляемости, на котором может быть идентифицирована функция r ( t ):

^S Д = ( t 0 ⁺ t Д ,t 1 ^- t Д ) , ⁽⁶⁾ где t Δ с одной стороны — время выжидания начала реакции пользователей сети на опубликованную новость. Идентификация активности пользователей до начала их реакции невозможна. С другой стороны — это время начала влияния члена 2( v – v e ) в сопряжённой задаче на всю пространственную область рассматриваемого кластера сети.

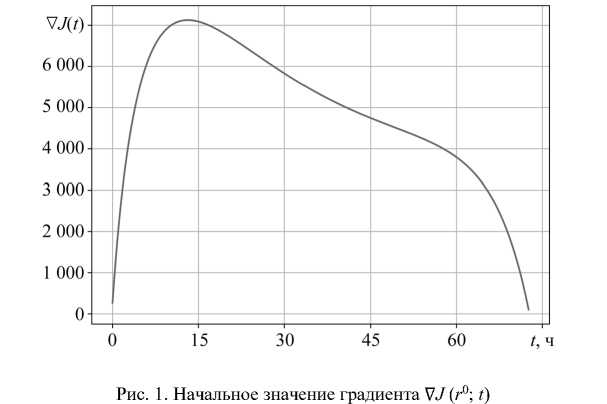
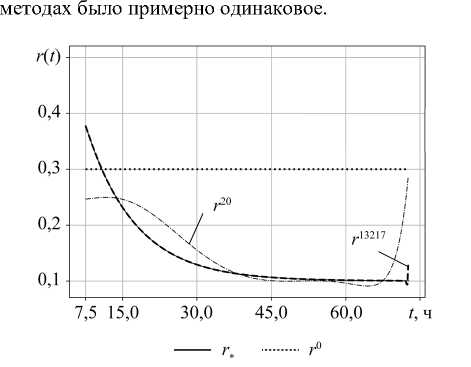
На рис. 1 показано начальное значение градиента. Результаты идентификации представлены на рис. 2 а . Сходимость метода завершилась на итерации k = 13 217 с неравномерной на S Δ сходимостью. Штрихпунктирная кривая — это пример значения функции r ²⁰( t ) на 20-й итерации.

Информатика, вычислительная техника и управление

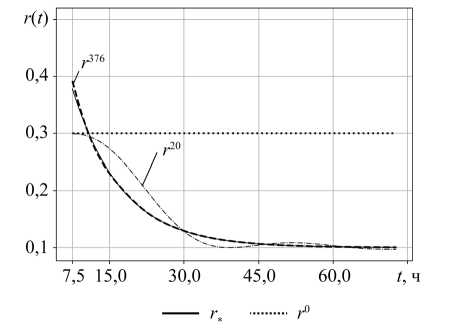
Результаты идентификации МРНС представлены пунктирной кривой на рис. 2 б . Сходимость завершилась за k = 376 итераций. Полученная функция r 3 ⁷⁶( t ) визуально совпадает с точным тестовым значением r * ( t ). Штрихпунктирная линия — это пример r ( t ) на итерации k = 20. Конечное значение целевого функционала в обеих

• а) б)

Рис. 2. Идентификация r ( t ): a — посредством МНС; б — посредством МРНС

Обсуждение. Полученные результаты позволяют сделать ряд важных выводов о природе задачи идентификации и эффективности предложенного метода. Значительная неравномерность начального градиента ∇ J ( r ⁰; t ) (рис. 1) при равномерном начальном приближении r ⁰ ( t ) является прямым следствием пространственно-временной динамики модели (1) и ограниченной управляемости (6) системы на краях интервала S . Это объясняет, почему классический МНС, не учитывающий данную неоднородность, демонстрирует медленную и неравномерную сходимость (рис. 2 а ). Алгоритм тратит значительные вычислительные ресурсы на компенсацию особенностей градиента, что и приводит к необходимости 13 217 итераций.

В свою очередь, МРНС эффективно компенсирует эту неоднородность за счет параметра а( t ), адаптируя направление поиска к локальным особенностям функционала. Это подтверждается равномерной сходимостью r k ( t ) ^ r * ( t ) на всем множестве S д (рис. 2 б ) и сокращением числа итераций на два порядка (376 против 13 217). Данный результат хорошо согласуется с теоретическими предпосылками, изложенными в [12] , и подтверждает, что для бесконечномерных задач ключевым фактором является не просто минимизация, а учет неоднородности функционала градиента.

Что касается согласования с предыдущими исследованиями, успех в прямой идентификации r ( t ) развивает идеи, заложенные в [11] для идентификации h ( x ), и демонстрирует универсальность прямого экстремального подхода для функциональных параметров в распределенных системах. В то же время наш подход предлагает решение проблемы, обозначенной в [10] , где констатировалась неэффективность классических численных методов. Для сравнения: в работе [15] рассмотрены похожие проблемы для систем обыкновенных дифференциальных уравнений при идентификации вектора чисел. Было показано, что проблема не в самой задаче, а в необходимости применения специализированных адаптивных алгоритмов. Установление области идентифицируемости S _д также является важным методологическим вкладом. Этот результат подчеркивает фундаментальное ограничение, связанное с инерционностью процесса диффузии и временем установления реакции сети, что должно учитываться при корректной постановке подобных обратных задач.

Заключение. В данной работе была решена актуальная задача прямой параметрической идентификации функции активности пользователей r ( t ) в линейной диффузионной модели (1), описывающей распространение информации в социальной сети. Разработанный и верифицированный алгоритм на основе прямого экстремального подхода с регулируемым направлением спуска продемонстрировал более чем двукратное превосходство в скорости сходимости по сравнению с классическим градиентным методом, доказав свою высокую эффективность для этого класса задач.

Практическая значимость исследования заключается в создании вычислительного инструмента, который позволяет отказаться от априорных эвристических аппроксимаций параметров и перейти к прямому восстановлению функций, что значительно повышает точность и адекватность моделей распространения информации. Это открывает возможности для разработки более надежных систем прогнозирования и управления информационными потоками в социальных сетях.

Основным ограничением в текущей работе является использование синтетических данных для валидации метода. Также интерпретация физического смысла и размерности самой функции r ( t ) требует дальнейшего углубленного изучения. Дальнейшие исследования будут направлены на развитие модельных представлений и адаптацию доказавшего эффективность метода к более сложным нелинейным моделям. В качестве ключевой задачи на будущее рассматривается расширение метода для одновременной идентификации нескольких функциональных параметров, что представляет собой более сложную, но и более практически ценную задачу.