Идентификация коэффициентов интенсивности напряжений, T-напряжений и коэффициентов регулярных слагаемых высокого порядка в разложении Уильямса с помощью молекулярно-динамического моделирования
Автор: Степанова Л.В., Белова О.Н.
Статья в выпуске: 2, 2023 года.
Бесплатный доступ
Описан опыт применения метода молекулярной динамики для анализа поля напряжений в медной пластине с одним боковым горизонтальным и наклонным надрезами. Моделирование, основанное на методе молекулярной динамики и реализованное в классическом коде молекулярной динамики Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS), направлено на оценку параметров континуальной механики хрупкого разрушения, таких как коэффициенты интенсивности напряжений, T-напряжения и коэффициенты слагаемых более высокого порядка ряда Макса Уильямса, аппроксимирующего поле напряжений вблизи острия надреза для нормального разрыва (мода I), поперечного сдвига (мода II) и смешанного нагружения образца с одним боковым надрезом в условиях линейно-упругого деформирования. Ключевой целью исследования является сравнение континуального и атомистического подходов для оценки полей напряжений вблизи устья надреза на примере одной из наиболее распространенных конфигураций образцов с трещинами и надрезами. Коэффициенты интенсивности напряжений, Т-напряжения и коэффициенты регулярных слагаемых более высокого порядка в асимптотическом представлении Уильямса механических величин в медной пластине с одним боковым надрезом при нормальном отрыве и смешанном нагружении оцениваются с помощью дискретного подхода (атомистического моделирования) и континуального подхода (метода конечных элементов). Выполнен широкий класс молекулярно-динамических вычислений в LAMMPS. Атомистические значения коэффициентов интенсивности напряжений и коэффициентов неособых слагаемых более высокого порядка ряда Уильямса вычислены и сопоставлены со значениями, полученными из конечно-элементных решений. Показано, что континуальная теория разрушения успешно описывает поля вблизи вершины трещины даже при чрезвычайно ограниченном поле сингулярных напряжений, составляющем всего несколько нанометров. Угловые распределения компонент напряжений извлекаются из атомистического моделирования и сравниваются с угловыми распределениями напряжений континуальной механики линейного упругого разрушения. Сравнение показывает хорошее соответствие между двумя подходами.
Молекулярно-динамическое моделирование, коэффициент интенсивности напряжений, t-напряжения, коэффициенты регулярных слагаемых более высокого порядка ряда м. уильямса, смешанное нагружение, классическая механика разрушения
Короткий адрес: https://sciup.org/146282666
IDR: 146282666 | УДК: 639.3 | DOI: 10.15593/perm.mech/2023.2.06
Текст научной статьи Идентификация коэффициентов интенсивности напряжений, T-напряжений и коэффициентов регулярных слагаемых высокого порядка в разложении Уильямса с помощью молекулярно-динамического моделирования
PNRPU MECHANICS BULLETIN
Разрушения материалов происходят вследствие зарождения, слияния и распространения трещин, дефектов и вакансий и могут быть количественно описаны классической механикой разрушения, основанной на гипотезах и представлениях механики сплошных сред [1-4]. В традиционной континуальной механике хрупкого разрушения для характеристики полей напряжений, деформаций и перемещений вблизи вершин трещины и острых надрезов вводятся в рассмотрение коэффициенты интенсивности напряжений (КИН). Критерии традиционной линейной механики разрушения (ЛМР) используют интенсивность сингулярного поля напряжений вблизи вершины трещины, выражающуюся в терминах КИН [1-4]. Общеизвестно, что хрупкое разрушение может быть охарактеризовано сингулярным полем напряжений, коэффициент при сингулярном слагаемом и представляет собой КИН [1-4] (и ссылки внутри работ [1-4]). Однако с помощью представлений механики разрушения, основанной на идеях континуума, затруднительно прогнозировать разрушения материалов на наноуровне из-за дискретности строения кристаллической решетки [2]. Чтобы обеспечить физическое понимание явления разрушения на нано-скопическом уровне и тщательно изучить атомистическую природу разрушения, можно использовать атоми- стическое моделирование, основанное на методе молекулярной динамики (МД). До сих пор, преследуя данную цель, многие исследователи, основываясь на атомистическом моделировании, предприняли много успешных попыток рассчитать КИН и другие параметры механики разрушения [5-24]. В самой ранней, по нашим сведениям, работе 1983 г. [5] были смоделированы процессы распространения трещины с помощью двух сценариев: путем расклинивания и путем затупления вершины трещины вследствие зарождения и развития дислокаций в области нелинейного деформирования у вершины трещины с помощью МД-метода в альфа-железе и меди с применением потенциалов межатомного взаимодействия Леннарда - Джонса и Морзе соответственно. Моделирование показало, что альфа-железо, будучи по своей природе хрупким материалом, разрушается путем хрупкого расклинивания, когда КИН достигает своего критического значения. В работе [5] показано, что в железе не образуются дислокации, и даже развитие ограниченного двойникования вершин трещин в особых ориентациях не изменяет эту присущую железу хрупкость. В меди, которая по своей природе является пластичным материалом, затупление кончика трещины всегда предотвращает хрупкий рост трещины путем расщепления.
В исследовании [6] представлено атомистическое моделирование трещины отрыва, распространяющейся в гармонической решетке, основной целью этой работы является изучение полей напряжений и деформаций вблизи быстро распространяющейся трещины моды I. В статье получены атомистические КИН, которые далее сопоставляются с асимптотическими решениями механики сплошной среды для динамических упругих полей при различных скоростях распространения трещин. Авторы показывают [6], что как атомистическое напряжение, так и деформация могут быть последовательно связаны с соответствующими континуальными величинами. Исследование [6] демонстрирует, что результаты атомистического моделирования хорошо согласуются с выводами континуальной теории. Это означает, что теория континуума может быть применена к задачам наноразмерного масштаба.
Применимость континуальной механики разрушения в атомистических системах обсуждается в [7]. Авторы заключают, что энергетический баланс Гриффитса на наноуровне все еще действителен, но концепция механики разрушения сплошной среды не применима напрямую, поскольку размер зоны доминирования КИН чрезвычайно мал. Если вязкость разрушения оценивается на основе сингулярного поля напряжений для прогнозирования разрушения наноструктур, то необходимо учитывать двухпараметрическую модель, включающую вклад несингулярных членов в упругое решение, основанное на приближенном разложении Уильямса.
В работе [8] отмечается, что значения КИН используются в континуальной механике разрушения для количественной характеристики полей напряжений, окружающих кончик трещины в однородном линейно упругом материале. Критические значения КИН характеризуют внутреннюю меру сопротивления материала распространению в нем трещины. Авторы подчеркивают, что на атомистических масштабах разрушение происходит как серия разрывов атомных связей, что не может быть описано в континуальной теории. Авторы работы [8] представляют новый численный метод определения КИН на основе моделирования методом МД. Используя атомистические координаты частиц для описания поля перемещений вокруг вершины трещины, метод проецирует наблюдаемые перемещения на набор непрерывных полей перемещений, определяемых разложением Уильямса континуальной механики разрушения. Авторы сохраняют два члена разложения Уильямса и вычисляют их с помощью метода МД. Точность применяемого подхода сначала проверяется на простой модели, а впоследствии применяется к дискретному моделированию разрушения в аморфном кремнеземе. Моделирование методом МД обеспечивает значения зависящих от времени и пространства КИН, которые, как показано, хорошо согласуются с экспериментальными значениями вязкости разрушения в кварцевом стекле. Главной целью статьи [9] является исследование обоснованности применения методологии линейной механики разрушения, зиждущейся на концепции сплошной среды, к наноразмерным объектам и процес- сам, протекающим на наноуровне. Авторы сравнивают оценки J-интеграла, полученные с помощью атомистического моделирования, с результатами континуальной теории. Результаты [9] показывают значительное отклонение молекулярно-динамических расчетов J-интеграла от значений макроскопической механики разрушения для длин трещин ниже определенного порога. Ввиду принципиальных различий между континуальным и атомистическим подходами в [9] обсуждается вопрос о том, следует ли применять концепцию, основанную на континууме, к дискретной системе и можно ли вычислить параметры механики разрушения на основе моделирования методом МД. Из этого явствует, что для подтверждения выводов необходимо провести широкое и скрупулезное моделирование методом МД. Это должно быть сделано самым тщательным образом во избежание ошибок при сравнении результатов континуального и атомистического подходов [9]. На основании выполненных объемных МД-расчетов авторы [9] заключают, что скорость высвобождения энергии деформации можно рассматривать как физическую величину, с помощью которой возможно установление связи между атомистическим моделированием и континуальным моделированием разрушения 2П-структур на примере разрушения листа графена.
Параметры разрушения листа графена с использованием атомистического моделирования и подходов механики сплошных сред оцениваются в работе [10]. Авторы отмечают, что ввиду дискретной структуры материала вблизи вершины трещины нет сингулярности напряжений, и делают вывод, что концепция КИН, которая обычно используется в механике разрушения, может не подходить для моделирования поведения трещины в листе графена на атомистическом уровне. Поэтому авторы обращаются к концепции скорости высвобождения энергии деформации и для ее подтверждения анализируют процесс разрушении листа графена с центральной трещиной с использованием атомистического моделирования и ЛМР и оценивают изменение энергии до и после продвижения трещины как в континуальной, так и в атомистической моделях. В рамках атомистического моделирования графен рассматривался как атомистическая структура с дискретными атомами углерода, тогда как в рамках континуальной механики разрушения графен моделировался как изотропная однородная среда. Авторы делают вывод [10], что скорость высвобождения энергии деформации можно рассматривать как физическую величину, которая устанавливает связь между атомистическим моделированием и континуальным описанием разрушения ковалентно связанного графенового листа. Стоит отметить, что статья [10] была мотивирована более ранними работами [11; 12], в которых исследуются макроскопические параметры разрушения, найденные как из атомистической, так и из континуальной модели. Результаты, полученные в [11; 12], показывают, что поле напряжений вблизи вершины трещины, вычисленное на основе атомистического моделирования, хорошо согласуется с полем напряжений континуальной механики.
В работе [11] представлено наноскопическое моделирование разрушения 2D-графеновых систем, содержащих трещины атомного масштаба, и исследованы макроскопические параметры разрушения. В дискретном атомистическом моделировании межатомные силы описываются потенциалом Терсоффа - Бреннера. Разработаны два метода расчета скоростей упругого высвобождения энергии в атомных системах, такие как метод глобальной энергии и метод локальных сил. Значения скоростей выделения энергии нескольких графеновых систем при симметричной (мода I) и антисимметричной (мода II) малой деформации получены из атомистического моделирования, а затем сравниваются с результатами, полученными с помощью гомогенизированных свойств материала на основе ЛМР. Результаты показывают хорошее согласие между дискретным атомистическим и континуально-механическим моделированием разрушения. Поля атомистических напряжений в окрестности вершины трещины исследуются с помощью моделирования молекулярной механики с применением приложенной на бесконечности деформации с заданным КИН. Распределения атомистических напряжений очень хорошо совпадают с распределениями, диктуемыми линейной теорией упругости. Эти результаты устанавливают связи параметров разрушения при микроскопическом и макроскопическом описаниях разрушения в ковалентно связанных твердых телах.
В статье [12], где распространение трещины в графитовом листе в миллион атомов исследуется с помощью МД-моделирования, основанного на эмпирическом потенциале Бреннера, показано, что локальное напряжение вблизи вершины трещины может быть хорошо описано классической особенностью поля напряжений, обратно пропорциональной квадратному корню из расстояния от кончика трещины.
В работе [13] изучается новый графеноподобный двумерный материал и его механические свойства. Нанолист с критическими дефектами, такими как линейные трещины и зазубрины, моделируется с помощью МД-метода. Для прогнозирования механического отклика при различных температурах при одноосном растяжении учитывались различные длины трещин и диаметры надрезов. Авторы рассчитали критическое значение КИН для одной геометрии трещины при разных температурах. Авторы не используют распределения напряжений, полученные в результате моделирования методом МД. Использована аналитическая оценка ЛМР для КИН в пластине с периодической системой трещин при нагружении отрывом. Таким образом, критическое значение КИН оценивается путем подстановки напряжения, соответствующего разрушению, полученного с помощью моделирования молекулярной динамики, ширины нанолиста и начальной длины трещины в формулу континуальной ЛМР. Авторы показывают, что КИН лишь незначительно уменьшается с повышением температуры. Однако сравнение континуальных полей напряжений и атомистических полей в [13] отсутствует.
В целом было опубликовано много исследований, посвященных моделированию двумерных нанослоев с помощью метода МД [14-21]. В работе [14] МД моделирование было использовано для вычисления вязкости разрушения, определения механических свойств и поведения распространения трещин дефектных монослоев графеноподобных наноструктур оксида бериллия. Критическое значение КИН рассчитывалось в соответствии с ЛМР. Таким образом, авторы предполагают, что континуальная механика разрушения может быть применена для характеристики поля напряжений на атомистическом масштабе.
Чтобы получить полное изображение наноструктуры поликристаллических нанолистов оксида бериллия под нагрузкой, в исследовании [15] с использованием МД-метода был смоделирован процесс разрушения наноскопического листа оксида бериллия. Получены критические значения КИН для образцов с периодической системой трещин в соответствии с ЛМР. Авторы статьи [15] используют подход, аналогичный идее, разработанной в [14]. Используется теоретический результат для КИН из ЛМР. Таким образом, авторы неявно принимают гипотезу, согласно которой ЛМР работает в рассматриваемых масштабах, а поля напряжений у вершины трещины могут быть охарактеризованы КИН теории разрушения механики сплошных сред.
МД-моделирование было использовано в [16] для изучения механики монокристаллических и поликри-сталлических кремний-германиевых нанослоев в зависимости от температуры. Критический КИН образцов с трещинами оценивается как функция температуры. ЛМР используется для расчета критического КИН для пластины с периодической системой трещин.
Механические свойства и поведение при разрушении поликристаллических нанослоев BC3 были исследованы с использованием метода МД в работе [17]. Как и в предыдущих исследованиях [14-16], рассчитаны критические значения КИН образцов с трещинами при различных температурах. Напряжение разрушения определяется с помощью моделирования методом МД, тогда как КИН оценивается по формуле ЛМР. Таким образом, авторы не анализируют распределение напряжений вблизи вершины трещины. Априори предполагается, что механика сплошных сред может быть использована на наноуровне, а обычные параметры механики разрушения могут быть использованы для характеристики атомистического моделирования.
Исследование [18] направлено на изучение механических свойств и поведения при разрушении моно- и поликристаллических нанолистовых материалов BC3. Авторы [18] также рассчитывают критические значения КИН, но, в отличие от предыдущих работ [14-17], они изучают образцы с краевыми трещинами разной длины. Для получения критических значений КИН значения напряжений при разрушении были извлечены из меха- нических свойств, полученных с помощью моделирования методом МД.
Статью [19] можно отнести к аналогичному классу работ [14-18], в которых моделирование методом МД применяется для исследования разрушения моно- и по-ликристаллических нанослоев. Авторы отмечают, что графеноподобные нанолисты являются ключевыми элементами современных материалов и систем. Авторы отмечают, что механические свойства структурно совершенных двумерных наноструктур, включая модуль Юнга, напряжение и деформации при разрушении, хорошо документированы, а свойства поликристалличе-ских наноструктур менее изучены. Таким образом, методом МД моделируются поликристаллические наноли-стовые структуры. Аналогично работам [14-18] оцениваются критические КИН для нанолиста, обладающего центральной периодической системой трещин.
Отличительной особенностью работ [14-19] является применение метода МД для компьютерного моделирования разрушения двумерных структур и использование обычных параметров ЛМР для характеристики разрушения.
Распространение краевых трещин в монокристаллическом альфа-кварце в условиях нагружения, соответствующих моде I, было исследовано в работе [20] с использованием МД моделирования. Пять различных длин трещин используются для анализа влияния длины трещины на поведение роста трещин в каждом образце. Влияние длины трещины изучалось с точки зрения кривой «напряжение - деформация» материала, энергии деформации, вязкости разрушения, атомистического анализа распространения трещины и деформации раскрытия трещины. Результаты показали, что при растяжении образцы кристаллического кварца с трещинами разрушаются хрупким образом. Напряжение при разрушении в образце с предварительно внесенной трещиной (длина 40 Å) снижается примерно на 70 % по сравнению с целым, исходным (неповрежденным) кварцем. Кроме того, исследуется влияние скорости нагружения на механические свойства. Согласно полученным результатам, максимальное напряжение повышается за счет увеличения скорости нагружения, также растет вязкость разрушения. Рассчитана поверхностная энергия разрушения монокристаллического альфа-кварца, и результаты демонстрируют хорошее согласие с экспериментальными данными. Показано, что с помощью моделирования методом МД можно определить КИН и независимый от пути J-интеграл [20].
В работе [21] моделирование методом МД используется для исследования деформирования и разрушения монокристаллического алюминия. КИН оценивается с помощью четырех различных техник, для каждого подхода приведена оценка точности метода и значения вязкости разрушения. Предложенная методология также применяется для оценки вязкости разрушения графена и алмаза с использованием опубликованных данных из других источников. Полученная вязкость разрушения монокристаллического алюминия сравнивается с вязкостью разрушения других наноматериалов, имеющих сходную микроструктуру. Эмиссия дислокаций во время моделирования разрушения нанокристалла алюминия с трещиной анализируется для изучения поведения кристалла при разрушении. Обнаружено, что хрупкое разрушение является преобладающим режимом разрушения для наноматериалов, изученных в этом исследовании.
Моделирование МД было проведено с использованием потенциала Стиллингера - Вебера при комнатной температуре для изучения механических свойств и определения критического КИН моды I деформированных двумерных гексагональных листов моносульфида кремния и селенида германия в работе [22].
Опираясь на вышеозначенное, можно признать, что в работах [14-22] изначально принимается гипотеза о применимости ЛМР на наноуровне.
В [23] метод конечных элементов, базирующийся на молекулярно-динамических расчетах с потенциалами Терсоффа, использовался для определения КИН в условиях растяжения гексагональных листов силицена, нитрида алюминия и карбида кремния. Обнаружено, что KIct ( KIc - критическое значение КИН для моды I, а t -толщина листа) для листов силицена, нитрида алюминия и карбида кремния составляет примерно 80, 66 и 47 % и на 73, 64 и 45 % меньше значений для графена для трещин, ориентированных вдоль кресельных и зигзагообразных направлений соответственно. Таким образом, в работе [23] оцениваются критические значения КИН. Определение критического значения КИН основано на представлении поля перемещений вблизи вершины трещины классической ЛМР. Поле перемещений вблизи вершины трещины было использовано для определения критических размеров графена в [24], где представлена методика изучения разрушения в наноматериалах путем объединения квантовой механики и механики сплошных сред. Таким образом, критические значения КИН для краевой трещины длиной 11,4 нм были вычислены с различными размерами квантовых доменов. Домен содержал от 110 до 210 атомов. Несмотря на это, показано, что КИН имеет смысл, а критический КИН не чувствителен к размеру области квантовой механики для кресельных трещин. Таким образом, характерной особенностью исследований [14-24] является вычисление критических значений КИН посредством формул континуальной механики разрушения, но напряжение при разрушении определялось путем атомистического моделирования.
Принципиально иной подход был реализован в работе [25], где изучается распространение трещин в однослойном графеновом листе с краевыми трещинами, деформируемом с постоянной скоростью деформации. В [25] используются LAMMPS и потенциал Терсоффа для нахождения КИН в условиях нагружения отрывом. Напряжения вычисляются по теореме вириала, исходя из МД-расчетов. Авторы заключают, что предложенный и использованный метод может быть применен для оценки КИН в любой наноструктуре.
В работе [26] также обсуждаются некоторые соображения о КИН в атомистическом масштабе. П. Галло отмечает [26], что недавние результаты показали обоснованность концепций КИН на атомистическом уровне. Основываясь на молекулярной статистике, автор формулирует два важных вывода: 1) анализ молекулярной статистики предсказывает не бесконечное напряжение вблизи вершины трещины, а скорее его конечное значение; 2) даже если сингулярность напряжения отсутствует вблизи области вершины трещины, напряжение все равно изменяется с сингулярностью квадратного корня.
В [27] разработана вычислительная схема, основанная на инвариантном J-интеграле на атомном уровне (или интеграле сохранения двух состояний) для анализа разрушения при смешанном нагружении вдоль границ зерен в поликристаллических твердых телах. Дискретная атомистическая информация, полученная в результате молекулярно-динамического моделирования распространения трещин вдоль границ зерен в поликри-сталлических твердых телах, объединяется с асимптотическими сингулярными полями вблизи вершины межфазной трещины между разнородными материалами в интеграле взаимности, построенным на основе общего J-интеграла на атомном уровне, для извлечения отдельных КИН первой и второй мод нагружения. В работе [27] показано, что этот метод выгоден для изучения межзеренного разрушения хрупких поликристаллических твердых тел в атомном масштабе, поскольку распространение трещины вдоль границ зерен обычно можно рассматривать как разрушение в смешанном режиме.
Вычислительные исследования поведения трещины в смешанном режиме нагружения методом МД и многопараметрическое описание поля трещины классической механикой разрушения выполнены в [28-31]. Показано, что углы направления распространения трещины, полученные МД-моделированием, очень близки к углам, предсказанным ЛМР. В статье [31] представлен анализ поля напряжений вблизи устья трещины методом МД, реализованным в классическом коде, осуществляющем метод МД LAMMPS (Large-scale Atomic/ Molecular Massively Parallel Simulator). МД-моделиро-вание направлено на вычисление параметров механики разрушения. КИН для монокристаллической ГЦК медной пластины с центральной трещиной при растяжении и смешанных нагружениях оцениваются с помощью атомистического моделирования. Реализован широкий класс вычислительных экспериментов в LAMMPS. Атомистические значения коэффициентов интенсивности напряжений сравниваются со значениями, полученными из классических критериев континуальной механики разрушения. Показано, что теория разрушения механики сплошной среды успешно описывает разрушение даже при чрезвычайно ограниченном сингулярном поле напряжений, составляющем всего несколько нанометров.
В [32] предложен многомасштабный метод, основанный на репрезентативном элементе объема, для ис- следования механизма распространения усталостных трещин путем МД-моделирования и расширенным методом конечных элементов (extended finite element method - XFEM). Построена атомистическая модель пластины из углеродистой стали для изучения поведения усталостной трещины в микромасштабе методом МД. Авторы полагают, что КИН может быть получен в LAMMPS, поскольку LAMMPS может вычислять атомистические напряжения. Более того, авторы показывают, что константы закона Пэриса могут быть вычислены по результатам МД-моделирования, а затем константы могут быть переданы в XFEM для расчета срока службы образца. Таким образом, закон Пэриса можно рассматривать как связующее звено между методами XFEM и МД.
Тем не менее до сих пор обсуждается вопрос, следует ли применять основанное на континууме понятие, такое как напряжение, к дискретным системам, состоящим из атомов [33-37].
Таким образом, несмотря на широкий спектр исследований, посвященных этой теме, можно сделать вывод, что остаются пробелы, которые необходимо изучить и проанализировать, чтобы полностью понять взаимосвязь между различными уровнями протекания процессов разрушения, их инициацией и эволюцией. В настоящее время нет единой точки зрения на возможность использования континуальной механики разрушения для описания процессов разрушения на атомном уровне. С одной стороны, классическая механика разрушения предоставляет исследователю глубокую и хорошо разработанную теоретическую базу, с другой стороны, метод МД предоставляет практически неограниченные вычислительные возможности для компьютерных экспериментов. Разумное сочетание и применение обоих подходов позволяют изучать процессы разрушения одновременно на каждом из уровней и учитывать взаимное влияние этих процессов. В настоящей работе реализован подход, основанный на широких и тщательных вычислительных экспериментах, с целью нахождения атомистических КИН и масштабных (амплитудных) коэффициентов слагаемых более высокого порядка разложения Уильямса из атомистического исследования, выполненного в LAMMPS с использованием модельного материала (в качестве которого была избрана монокристаллическая ГЦК-медь).
Таким образом, применимость континуальной механики разрушения в атомистических системах по-прежнему заслуживает и требует глубокого рассмотрения и тщательного анализа. Механика сплошных сред предоставляет множество аналитических решений и хорошо разработанных методов, которые мы хотели бы использовать на наноуровне. Одним из таких решений механики хрупкого разрушения является классическое асимптотическое представление Уильямса поля напряжений вблизи острия трещины или надреза. Поэтому в текущем исследовании мы стремимся проанализировать возможность применения классической механики раз- рушения для описания процессов разрушения на нано-скопическом уровне, а именно применение многопараметрического разложения Уильямса механики сплошных сред для описания полей напряжений вблизи трещины на наноуровне с помощью МД-моделирования. Поля напряжений вблизи кончика надреза будут определены с использованием двух подходов: континуального и атомистического. В рамках континуального подхода для вычисления полей напряжений используется метод конечных элементов, а коэффициенты многопараметрического разложения Уильямса вычисляются с использованием алгоритма переопределенного метода, тогда как в рамках атомистического подхода также используется процедура переопределенного метода, но применяются атомистические поля напряжений, найденные с помощью молекулярно-динамического моделирования с учетом влияния дискретности строения кристаллической решетки.
В целом первоначальная мотивация для этого исследования была тройственной. Первой мотивацией является взаимное сравнение зависимостей компонент тензора напряжений от полярного угла вблизи вершины трещины, полученных из концепций механики сплошных сред, и окружных зависимостей атомистических напряжений вокруг вершины трещины, полученных с помощью моделирования молекулярной динамики. Вторая причина заключается в вычислении коэффициентов более высокого порядка разложения в ряд Уильямса с использованием двух совершенно разных подходов, континуальных и атомистических методов, а также возможности описания свойств и особенностей поля напряжений у вершины трещины с использованием разложения Уильямса на атомистическом уровне. Третья мотивация исходит из очевидной необходимости объединения метода МКЭ и метода МД, создания многомасштабных параллельных атомистически-контину-альных моделей, сочетающих континуальное и атомистическое моделирование [38-42].
Следовательно, основная цель настоящего вычислительного анализа заключается в определении КИН и коэффициентов членов более высокого порядка разложения Уильямса для нагрузок во всем диапазоне параметра смешанности нагружения, описывающего вид смешанного режима нагружения, с помощью атомистического моделирования и сравнении результатов с коэффициентами разложения Уильямса, известными из ЛМР [1] для пластины с боковым надрезом. Члены более высокого порядка могут вносить значительный вклад в описание поля напряжений вблизи вершины трещины. В настоящее время существует четкое понимание того, что необходимо учитывать члены более высокого порядка разложения Уильямса [3; 4]. Влияние слагаемых более высокого порядка проявляется, если необходимо расширить область, где справедливо решение Уильямса, на большие расстоянии от вершины трещины [3; 28-31; 42-44]. В настоящей работе слагаемые более высокого порядка ряда Уильямса учитываются при анализе, основанном как на механике сплошных сред, так и на дискретном подходе.
1. Асимптотические поля напряженийи перемещений вблизи острия трещины
Асимптотическое представление поля напряжений вблизи вершины трещины в линейных упругих изотропных средах получено Максом Уильямсом и активно используется в настоящее время [42; 43]. Разложение в степенной ряд Уильямса является основным асимптотическим представлением полей напряжений и перемещений вблизи вершины трещины в традиционной линейной механике разрушения [3; 4; 42-44]. Формальное степенное разложение поля напряжений в окрестности острия трещины в двумерном однородном изотропном линейно упругом теле, подвергнутом произвольному нагружению, являющееся линейной суперпозицией двух решений, соответствующих нормальному отрыву и поперечному сдвигу, может быть записано как:
о у ( r ,6) = z z a- m r /2 - 1 z mk ? ce), (1)
m = 1 к =-^
где r ,6 - полярные координаты; индекс m соответствует моде разрушения; a m - амплитудные коэффициенты, зависящие от геометрической конфигурации образца с трещиной, величины и моды нагружения; f m;j (6) - угловые функции, зависящие от моды и компонентов тензора напряжений. Аналитические выражения для угловых собственных функций f mkj (6) приведены в [43; 44]:
f (H)(6) = (к /2) [(2+к/2+(-1)к) cos( к/2-1)6-- (к/2-1)cos( к/2-3)6], f^H к/2) [(2-к/2-(-1)к) cos( к/2-1)6+ + (к/2-1)cos( к/2-3)6], f (1к2)(6) = (к /2) [-(к/2+(-1)к) sin( к/2-1)6+ + (к/2-1)sin( к/2-3)6], f2(, к) (6) = -(к / 2) [(2+к/2-(-1)к) sin( к/2-1)6-- (к/2-1)sin( к/2-3)6], f2(, 22(6)=-( к/2) [(2-к/2+(-1)к) sin( к/2-1)6+ + (к/2-1)sin( к/2-3)6], f^ 2(6) = (к/2) [-(к/2-(-1)к) cos( к/2-1)6+ + (к/2-1)cos( к/2-3)6].
Компоненты вектора перемещения в окрестности вершины трещины описываются как m=2 к=м
u( r ,6) = zz ( a m / G ) гк /2 g mк ) ( 6 ) , (4)
m = 1 к =-ro '
где используются следующие обозначения g^1) (0) = (к+k/2+(-1)k) cos (9/2) - (k / 2)cos( k / 2 - 2)9, g1(,2 (9) = (к-k/2-(-1)k)sin (9/2) + (k /2) sin(k / 2 - 2)9, g2k) (9) = -(к+k/2-(-1)k)sin (9/2) + (k / 2)sin(k / 2 - 2)9, g 2k2 (9) = (к-k/2+(-1)k) cos (9/2) + (k / 2)cos( k / 2 - 2)9.
Параметр к (постоянная плоской задачи линейной теории упругости) зависит только от коэффициента Пуассона для плоского деформированного к = 3 - 4v и плоского напряженного к = (3 - v) / (1 - v) состояний.
Коэффициенты akm представляют собой неизвестные параметры – амплитудные (масштабные) множители, обусловленные геометрией тела с трещиной и системой приложенных нагрузок, отражающие все многообразие задач механики хрупкого разрушения. КИН могут быть вычислены из коэффициентов как K I = a ^ V2k и K I =- a 2V 2K. Коэффициент a 2 связан с Т -напряжением как T = 4 a 12 . Важность членов более высокого порядка многоточечного разложения Уильямса для механических полей вблизи вершины трещины акцентируется многими исследователями [3; 4; 29–33; 43–48]. Можно утверждать, что мнение о необходимости сохранения слагаемых более высокого порядка в асимптотическом решении в настоящее время сформировано и подтверждено многими исследователями [3; 4; 28–32; 43–48]. Чем больше слагаемых сохраняется в асимптотическом решении (1), тем точнее будет описано поле напряжений вблизи вершины трещины. Аналитические [3; 4; 29–32; 45], экспериментальные [46; 47] и численные результаты [48–52] показывают, что одночленное и двухчленное решения могут привести к значительным ошибкам, а для достижения хорошей точности при расчете поля напряжений следует учитывать по крайней мере три члена или более в решении Уильямса в зависимости от расстояния до вершины трещины. Основная цель исследования заключается в том, чтобы определить коэффициенты akm более высокого порядка в разложении (1) для бокового надреза в пластине при нагружении растягивающей нагрузкой и смешанном нагружении. Смешанное нагружение описывается параметром смешанности
Ме = (2/n)arctg|lim ( о22( r ,9 = 0)/о12( r ,9 = 0))|. (7)
Коэффициенты разложения Уильямса для центральной трещины в бесконечной пластине при смешанной нагрузке известны и приведены в [43]:
a = ( - 1) n + 1 (2 n ^
2 n +1 1 2 3 n + 1/2( n !) 2 (2 n - 1) a n - 1,2,
a 2 = -CT 2 2 / 4,
1 a 2 k
= 0
для трещины нормального отрыва;
a 2 = n (2 n )^ Г 2
2 n+1 1 23 n+1/2( n !)2(2 n -1) an-1/2, a 2k = 0 (9)
для трещины поперечного сдвига, a – это длина трещины, о 2 2, ст ” 2 - приложенные напряжения на бесконечности. Представление поля напряжений в виде ряда (1)–(6) является мощным инструментом для надежного и точного описания напряжений вблизи вершины трещины [3; 4; 28–32; 46–52].
Таким образом, для бесконечной пластины с центральной трещиной существуют аналитические представления даже для коэффициентов более высокого порядка (8) и (9), тогда как для других конфигураций этот вопрос остается открытым. Вследствие чего целью данной работы является определение коэффициентов для пластины с одним боковым надрезом с использованием двух подходов. Первый из них – моделирование методом молекулярной динамики, второй основан на конечно-элементном подходе механики сплошной среды.
2. Молекулярно-динамическое моделирование 2.1. Определение упругих свойств материала
Во всех вычислительных экспериментах рассматривается медная пластина с одним боковым надрезом. Тензор упругих модулей может быть определен с использованием потенциальной энергии, вычисленной в ходе молекулярно-динамического расчета. Потенциальная энергия зависит от тензора деформации и может быть разложена в ряд Тейлора [53–55]
E (е) = E (0) + ZT-6f+ 7 ЁзЛт^ ^, (10) ,■=1 0£i 2= j=1 ebidej где E(0) – это энергия начального состояния равновесия, ei и ej являются деформациями в обозначениях Фойгта. Компоненты тензора упругих модулей могут быть вычислены по формуле
C jj
1 д 2 -
V d e i d e j
При моделировании различных видов нагружения были получены значения потенциальной энергии и деформации. По полученным данным была построена кривая зависимости энергии от деформации и проведена аппроксимирующая кривая. Коэффициент, стоящий во второй степени полиномиальной аппроксимирующей кривой, был подставлен в формулу (11). Таким образом, мы получили тензор упругих модулей (в ГПа):
|
" 167,25 |
123,81 |
123,81 |
0 |
0 |
0 Л |
|
|
123,81 |
167,25 |
123,81 |
0 |
0 |
0 |
|
|
123,81 |
123,81 |
167,25 |
0 |
0 |
0 |
(12) |
|
0 |
0 |
0 |
76,46 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
76,46 |
0 |
|
|
ч 0 |
0 |
0 |
0 |
0 |
76,46 ? |
Согласно схеме усреднения Хилла, используя найденные компоненты тензора упругих модулей, можно получить усредненные значения модуля Юнга = 125 ГПа, коэффициента Пуассона = 0,35, объемного модуля = 138,29 ГПа. Полученные значения упругих модулей хорошо согласуются с другими расчетами, например, приведенными с использованием ресурса ELATE для анализа тензора упругих модулей в [53–55]. Все вычисления были выполнены в открытом и мощном инструменте моделирования LAMMPS. Для вычисления свойств материала было выполнено моделирование с использованием потенциала внедренного атома (embedded atom model – EAM) Cu_u3.eam. Потенциал EAM является одним из наиболее широко распростра- ненных и часто используемых межатомных потенциалов, разработанных М. Доу и М. Баскесом [56]. Моно- кристаллическая медь имеет гранецентрированную кубическую структуру (face-centered cubic – fcc) с постоянной решетки 3,615 Å (рис. 1).
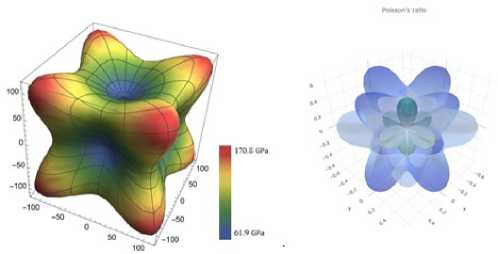
Рис. 1. Визуализация упругих свойств материала, обладающего кубической симметрией: модуль Юнга и коэффициент Пуассона кристалла меди
Fig. 1.Visualisation of elastic properties of a material with cubic symmetry: Young’s modulus and Poisson’s ration of single-crystal copper
-
2.2. Детали вычислений
В вычислительных экспериментах была выбрана fcc-медная пластина с одним боковым надрезом, чтобы провести сравнение между атомистическим полем напряжений и классическим разложением в ряд Уильямса (1)–(6). Общее число атомов в системе в численных экспериментах составило 321 602. Кристаллическая ориентация осей x 1, x 2 и x 3 была [100], [010], [001] соответственно. Длина надреза составляет 72,3 Å. Типичная пластина имеет размеры 723×723×7,23 Å в направлениях x 1, x 2 и x 3 соответственно (рис. 2). Как показано на рис. 2, трещина в атомной области моделируется путем разделения общей области на различные регионы. Области 1 и 2 , которые являются фиксированными слоями, состоят из атомов на верхнем и нижнем краях. Ограничивая взаимодействия между атомами в областях 3 и 4 (рис. 2), моделируется основная трещина. Область 5 представляет собой неповрежденную часть образца.
В соответствии с общей процедурой метода МД вычислительное исследование состоит из двух основных этапов [57]: процесс уравновешивания атомной структуры и механическое поведение пластины с надрезом в условиях смешанного нагружения. Для релаксации использовался канонический ансамбль NVE в течение периода 100 фс; временной шаг составлял 1 фс. Деформация пластины с надрезом осуществлялась путем ее растяжения и сдвига для моделирования смешанного режима нагружения. Напомним, что NVE – это классический микроканонический ансамбль системы с фиксированным числом атомов N, объемом V и полной энергией E, тогда как NVT – это классический микрокано-нический ансамбль с фиксированным числом атомов N, объемом V и температурой T соответственно.
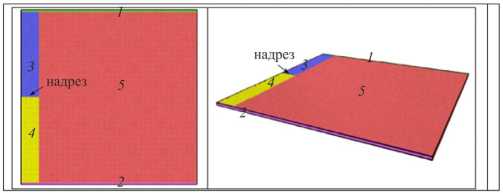
Рис. 2. МД-модель: схематическое изображение моделируемой геометрии
Fig. 2. MD simulation model: a schematic illustration of the simulation geometry
Периодические граничные условия были применены в направлении x 3 . Граничные условия по осям x 1 и x 2 не являются периодическими. Чтобы четко наблюдать упругий режим в атомном масштабе, температура имитационных моделей была выбрана равной 10 К. Для контроля над температурой используется NVE ансамбль с функцией для масштабирования температуры temp/ rescale. Параметр смешанности в МД моделировании определяется по формуле
Me = ( 2/л ) arctg ( e22 /e12 ) . (13)
Поскольку при моделировании МД скорость деформации задается в качестве граничных условий, удобнее использовать определение (13) для параметра смешанности нагружения, где s22 and e12 - приложенные скорости деформации. В описанном ниже анализе параметр смешанности определяется согласно формуле (13) вместо классического определения (7). Согласно (13), при вычислении параметра смешанности для ЛМР необходим коэффициент Пуассона. Механические свойства монокристаллической меди были определены с помощью МД ранее. Было найдено, что коэффициент Пуассона равен 0,35. Скорость деформации при нагружении по моде I равна s22 = 5,53 -10—2 5-1. Скорости деформации для смешанного нагружения задаются уравнением (13) для выбранного значения параметра смешанности M e . Скорости дефор- мации для Me = 0,66 были равны е12 = 3,19-10-2 5-1 и е22 = 5,53-10—25-1. Скорости деформации для Me = 0,5 полагались равными е12 = 2,76 -10—2 5-1 и е22 = 2,76 -10-2 5-1. Скорости деформации для Me = 0,33 были равны е12 = 5,53-10-25-1 и е22 = 3,19-10-25-1. Скорости деформации для Me = 0,16 устанавливались равными е12 = 5,53-10—25-1 и е22 = 1,48-10—25-1.
Таким образом, скорости деформации е 22 и е 12 варьировались от 3,19 - 10 — 2 5 - 1 до 5,53 - 10 — 2 5 - 1. Результаты моделирования показаны на рис. 3–7, где представлены морфология деформации и компоненты тензора напряжений для различных значений параметра смешанности нагружения. Изображения подготовлены в программе визуализации постобработки OVITO [58]. На рис. 3–7 показана концентрация напряжений вблизи вершины трещины на разных временных этапах.
15 пс
25 пс
30 пс
M e = 1
5 пс
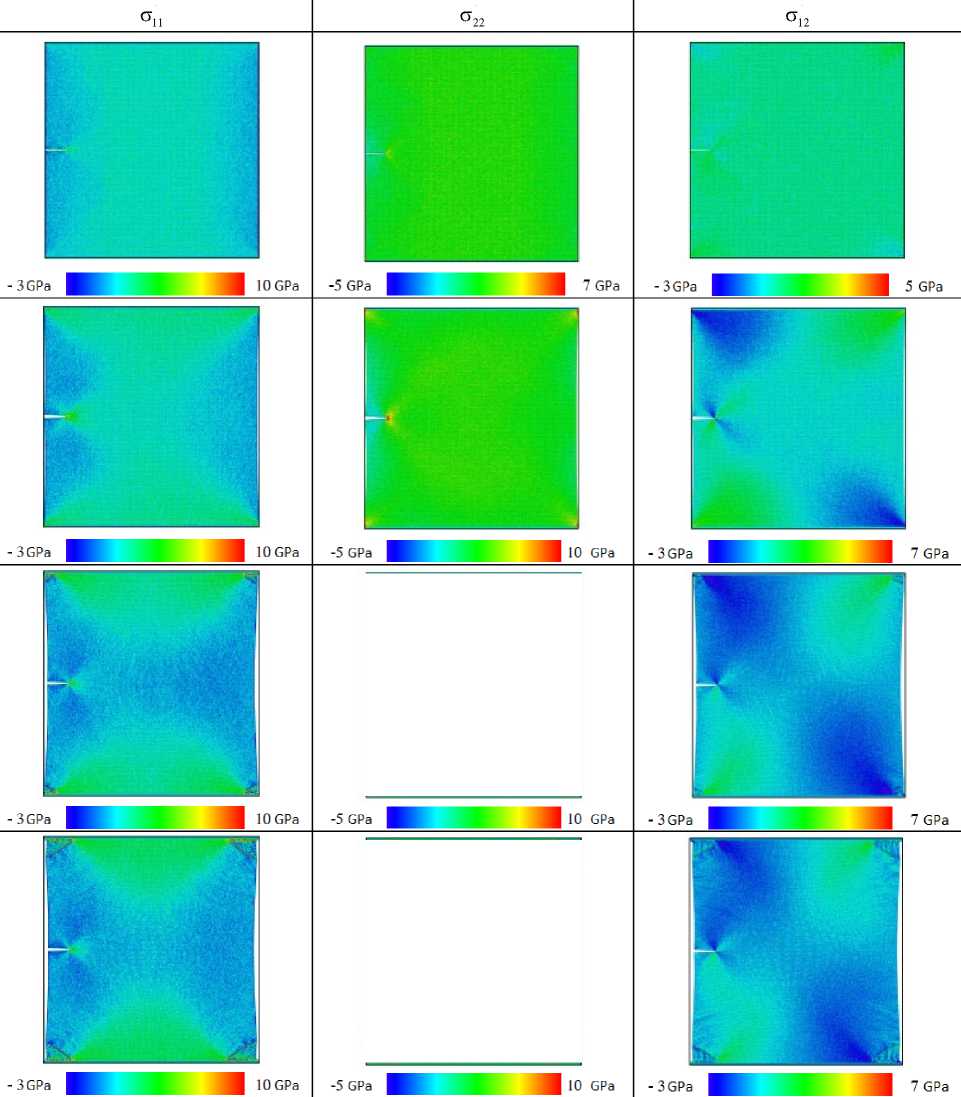
Рис. 3. Морфология деформации и компоненты тензора напряжений для параметра смешанности M e = 1 в моменты времени 5, 15, 25, 30 пс
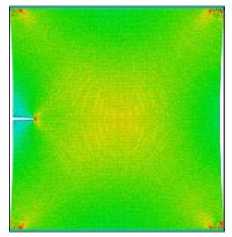
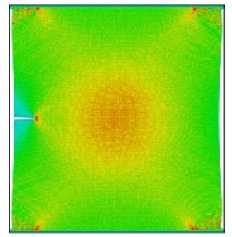
Fig. 3. The deformation morphology and the stress components for the mixity parameter Me = 1 at 5, 15, 25, 30 ps
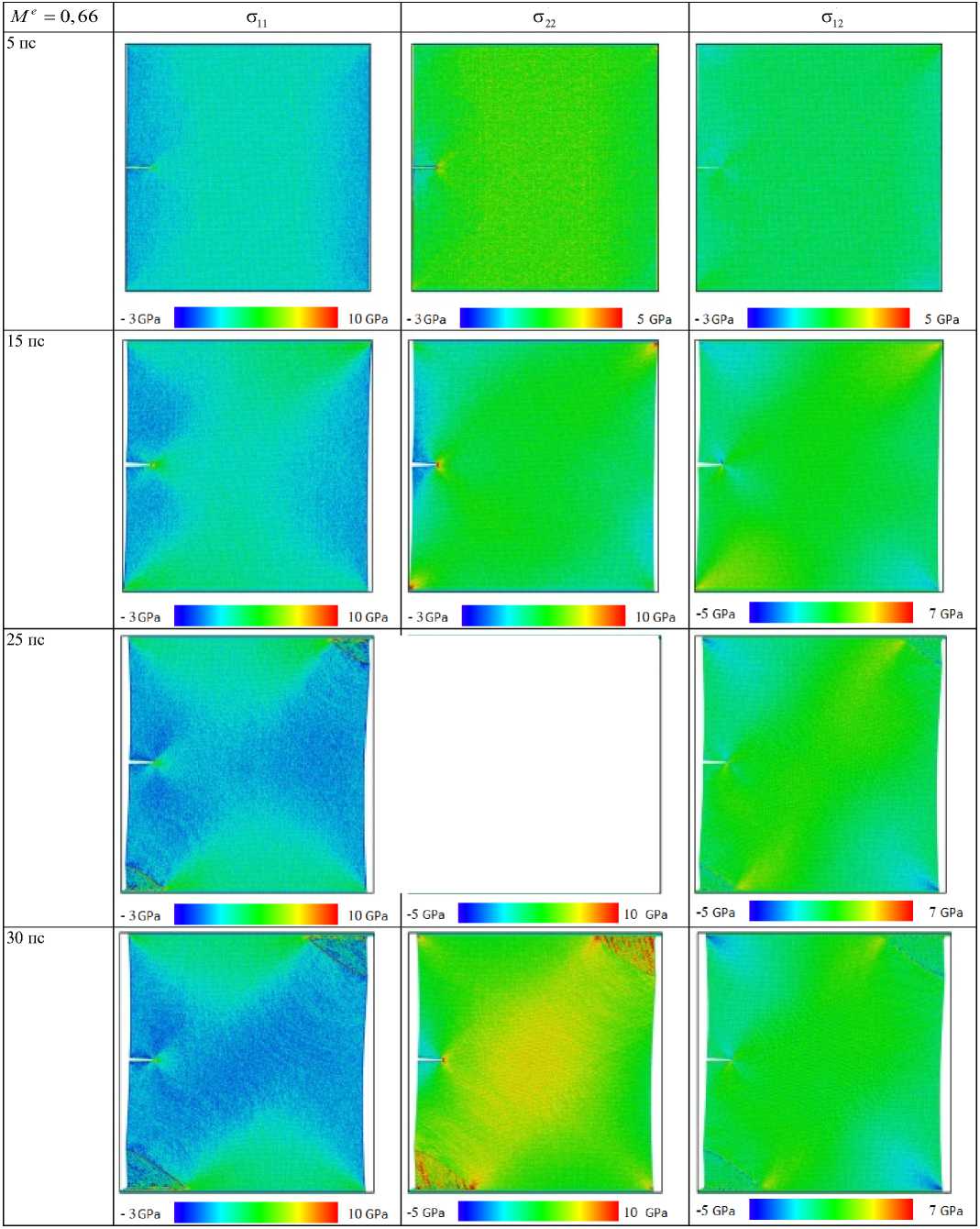
Рис. 4. Морфология деформации и компоненты тензора напряжений для параметра смешанности M e = 0,66 в моменты времени 5, 15, 25, 30 пс
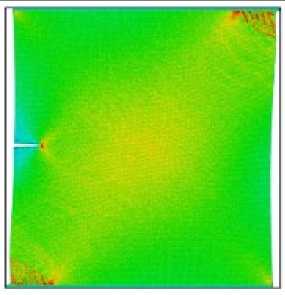
Fig. 4. The deformation morphology and the stress components for the mixity parameter M e = 0,66 at 5, 15, 25, 30 ps

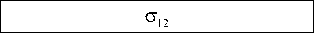
Me = 0,5
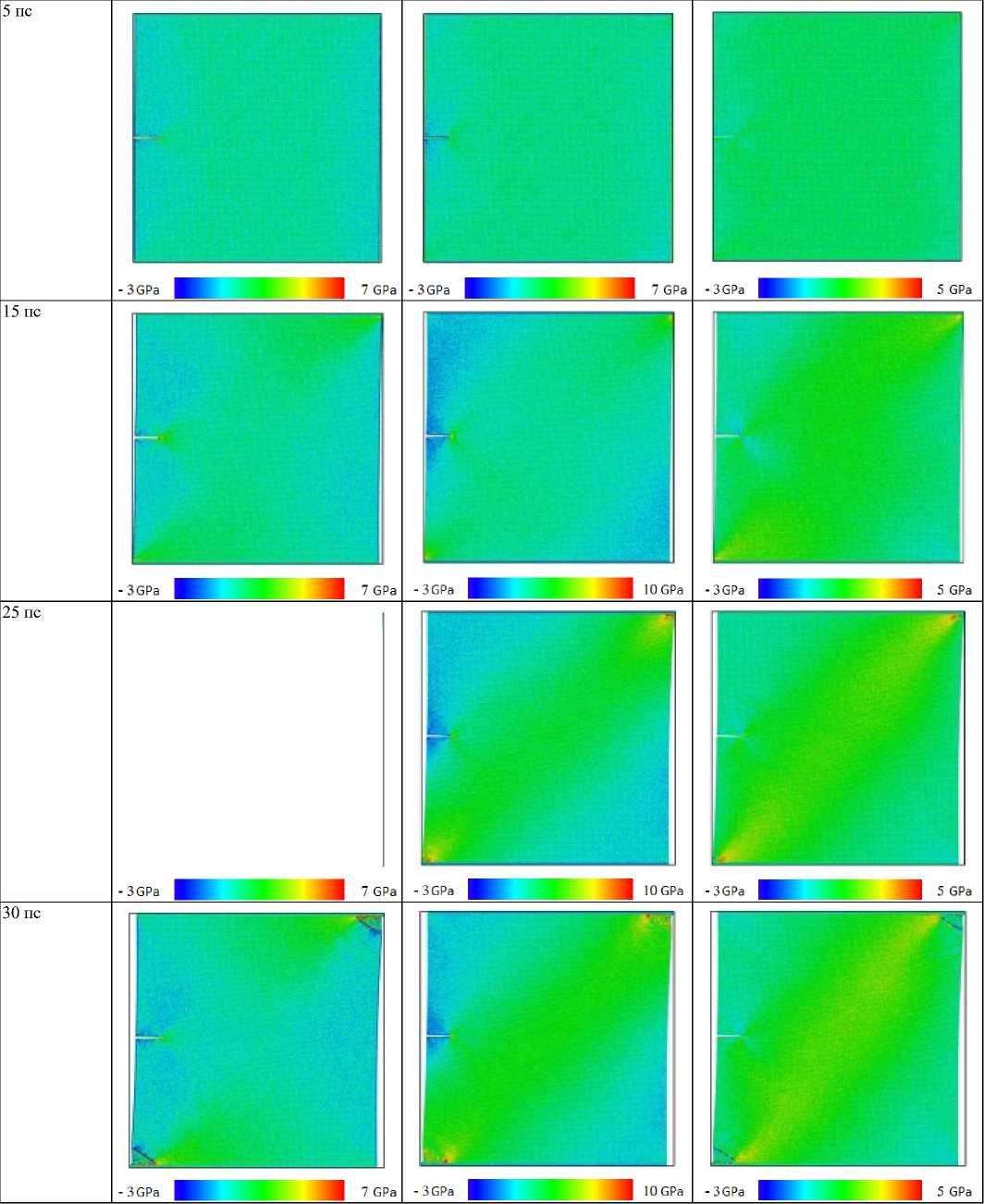
Рис. 5. Морфология деформации и компоненты тензора напряжений для параметра смешанности M e = 0,5 в моменты времени 5, 15, 25, 30 пс

Fig. 5. The deformation morphology and the stress components for the mixity parameter Me = 0,5 at 5, 15, 25, 30 ps
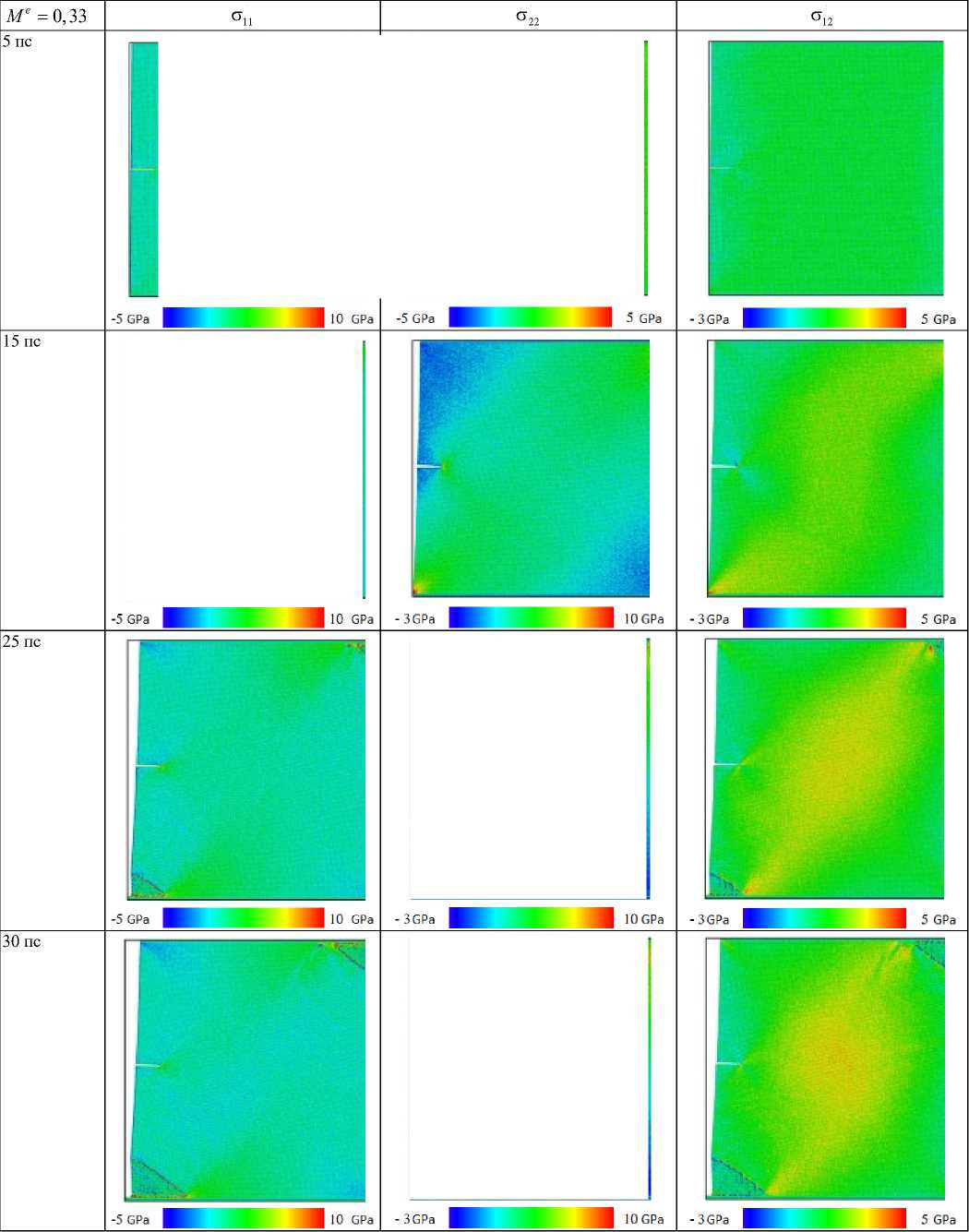
Рис. 6. Морфология деформации и компоненты тензора напряжений для параметра смешанности M e = 0,33 в моменты времени 5, 15, 25, 30 пс


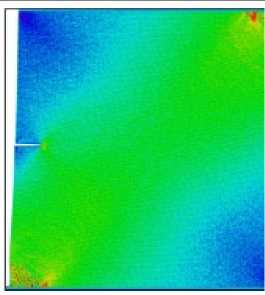
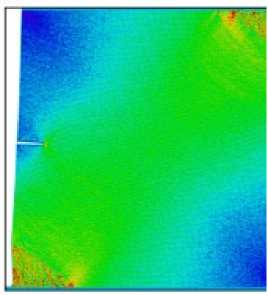
Fig. 6. The deformation morphology and the stress components for the mixity parameter M e = 0,33 at 5, 15, 25, 30 ps
e
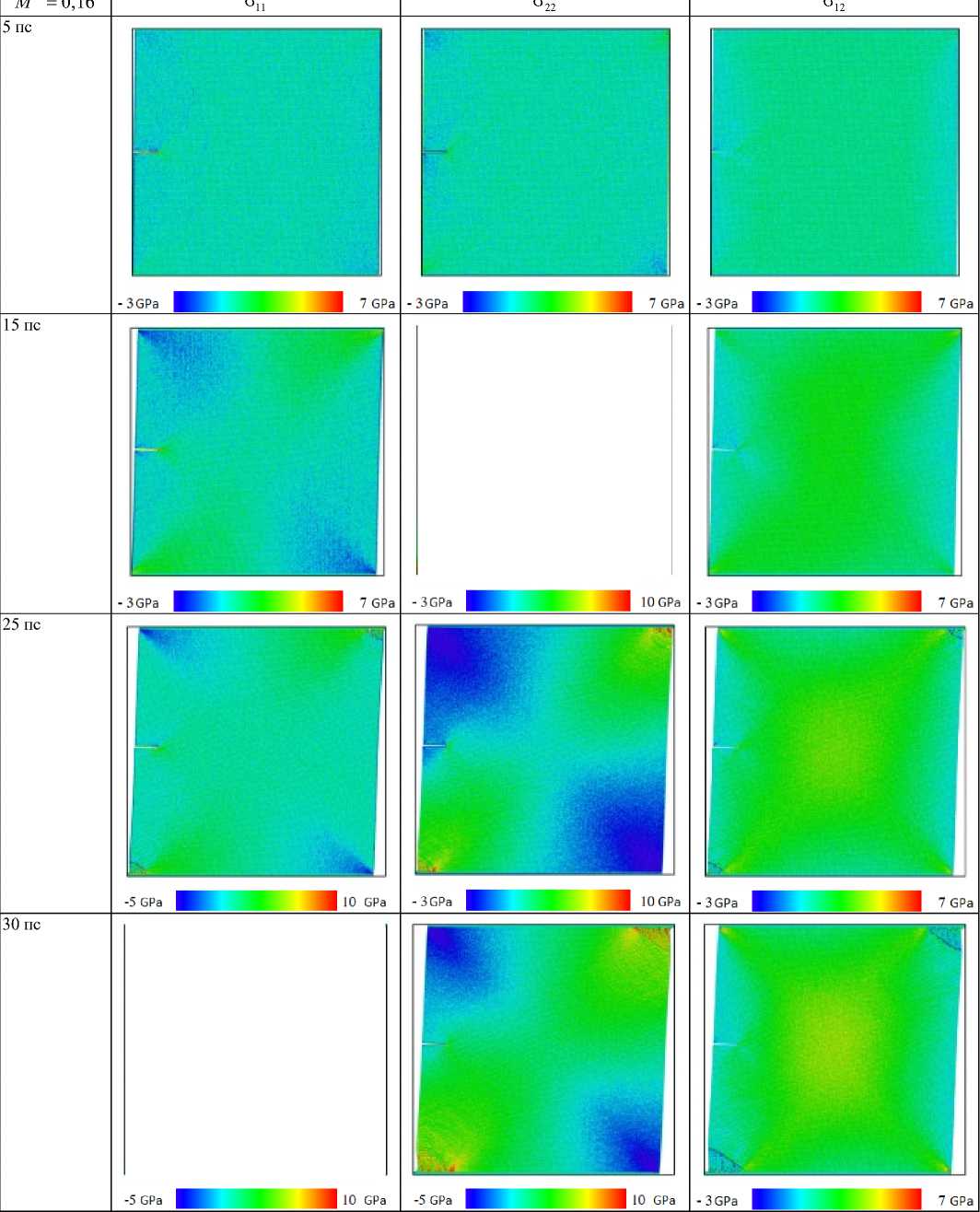
Рис. 7. Морфология деформации и компоненты тензора напряжений для параметра смешанности M e = 0,16 в моменты времени 5, 15, 25, 30 пс
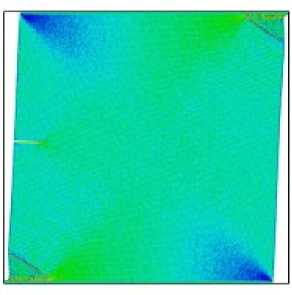

Fig. 7. The deformation morphology and the stress components for the mixity parameter M e = 0,16 at 5, 15, 25, 30 ps
Согласно этим рисункам, с увеличением временного шага концентрация напряжений вокруг кончика надреза увеличивается от низких (показанных синим цветом) до высоких (показанных красным цветом) значений. На рис. 3 показано распространение трещин и процесс разрушения медной пластины с боковым надрезом для моментов времени 5, 15, 25, 30 пс для Me = 1. Картины распространения трещины для параметра смешанности M e = 0,66 при 5, 15, 25, 30 пс показаны на рис. 4. Картины напряжений, полученные с помощью МД-моделирования для параметра смешанности M e = 0,5 при 5, 15, 25, 30 пс, показаны на рис. 5. Процесс разрушения и компоненты тензора напряжений для параметра смешанности M e = 0,33 при 5, 15, 25, 30 пс приведены на рис. 6. На рис. 7 показана медная пластина с боковым надрезом для параметра смешанности M e = 0,16 в моменты времени 5, 15, 25, 30 пс. Можно видеть, что у вершины надреза формируется область с высокими значениями напряжений, а контуры линий равных значений напряжений в моменты времени 25 и 30 пс аналогичны контурам решения механики сплошной среды при соблюдении упругого режима деформирования.
Компоненты тензора напряжений, полученные с помощью молекулярно-динамического моделирования, используются для вычисления атомистических параметров разрушения и сравниваются параметрами механики разрушения сплошных сред, вычисленных с помощью МКЭ.
3. Конечно-элементный анализ
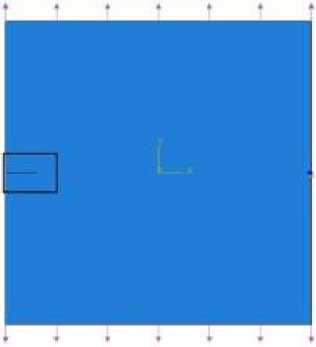
В настоящей части работы метод конечных элементов (МКЭ), популярный численный метод механики сплошных сред, является основным методом вычисления коэффициентов интенсивности напряжений, T-напряжений и коэффициентов более высокого порядка ряда Уильямса для полей напряжений и перемещений вблизи вершины бокового надреза в пластине. Геометрия модели для нормального отрыва и приложенные нагрузки показаны на рис. 8, а . Постоянные материала совпадают с параметрами моделирования, избранными в методе молекулярной динамики. На рис. 8, b , показана интенсивность напряжений фон Мизеса вблизи вершины надреза в условиях нормального отрыва. На рис. 8, c–f , показаны эквивалентные напряжения фон Мизеса вблизи вершины надреза при смешанной нагрузке для различных значений параметра смешанности. Выделенная область на рис. 8, b–f , представляет собой прямоугольную область на пластине, показанную на рис. 8, а .
Для моделирования смешанного нагружения при различных значениях параметра смешанности M e рассматривается наклонный надрез. Каждый угол наклона у (угол между горизонтальной осью и вырезом) соответствует определенному значению параметра смешан- ности нагружения Me. Угол наклона у и значение параметра смешанности нагружения M e связаны формулой Me = 1 - 2у / л , следующей из (7).
Для получения коэффициентов akm разложения Уильямса (1) из конечно- элементных расчетов был выбран набор точек, принадлежащих концентрическим окружностям, охватывающим вершину надреза. Количество точек варьировалось от 219 до 1757. Затем используется переопределенный метод (ПМ), основанный на значениях компонент напряжений в выбранных точках, полученных методом конечных элементов. Таким образом, масштабные коэффициенты асимптотического разложения поля напряжений у вершины надреза оцениваются из результатов анализа МКЭ. Переопределенный метод восходит к работе [59] и подробно описан в [60].
В соответствии с процедурой ПМ асимптотическое решение Уильямса (1)–(3) может быть представлено в матричном виде о = CA , (14)
где σ – вектор, состоящий из вычисленных компонентов тензора напряжений с помощью моделирования МКЭ. Матрица C представляет собой прямоугольную матрицу размерностью 3 M х ( K + L ) и A представляет собой вектор, состоящий из неизвестных параметров моды I и моды II a 11, a 12,..., a 1 K , a 12, a 22,..., aL 2. Здесь K – количество удерживаемых слагаемых в разложении Уильямса для нагрузки по моде I и L – количество слагаемых в разложении Уильямса для нагружения по моде II и M – количество экспериментальных точек. Таким образом, учитываются все компоненты тензора нормальных и касательных напряжений для пластины с надрезом. Значения масштабных множителей оцениваются путем минимизации целевой функции
J ( A ) = (1/2) ( о - CA ) T ( о - CA ) . (15)
Целевая функция (15) представляет собой квадратичную форму относительно неизвестных параметров A . Стоит отметить, что в этом случае для параметров A существует решение в замкнутой форме: A = ( CTC ) - 1 C T o.
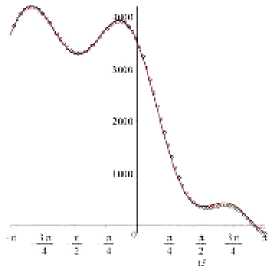
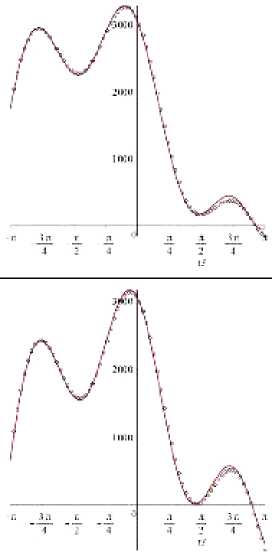
Затем усеченное разложение Уильямса (1), в котором сохранены пятнадцать слагаемых, используется для определения угловых распределений компонент тензора напряжений, показанных красными линиями на рис. 9 и 10. Черными точками на рис. 9 и 10 показаны результаты конечно-элементного анализа. Коэффициенты разложения Уильямса поля напряжений у вершины трещины нормального отрыва, рассчитанные с помощью МКЭ и последующем применением ПМ, приведены в табл. 1. Из рис. 9 видно, что разложение в пятнадцатичленный ряд Уильямса точно описывает поле напряжений вблизи вершины надреза. Восстановленное поле напряже- ний, показанное красным цветом, полностью совпадает с распределениями, найденными методом конечных элементов. Тщательный численный анализ поля напряжений и разложения М. Уильямса показал, что меньшее число членов в разложении ряде Уильямса приводит к значительным расхождениям с МКЭ [61]. На рис. 10
показаны угловые распределения компонент тензора напряжений в случае смешанного режима нагружения при различных значениях параметра смешанности нагружения. На рис. 10 можно увидеть, что восстановленное поле напряжений (1) с членами более высокого порядка полностью совпадает с численным решением.
а
Me = 1

b
Me = 0,66
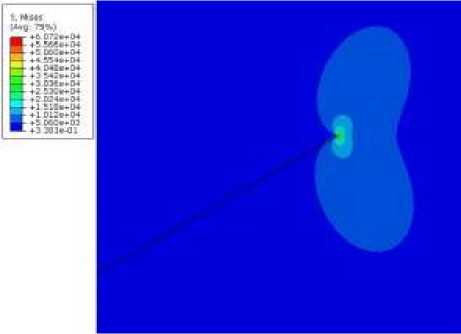
Me = 0,5
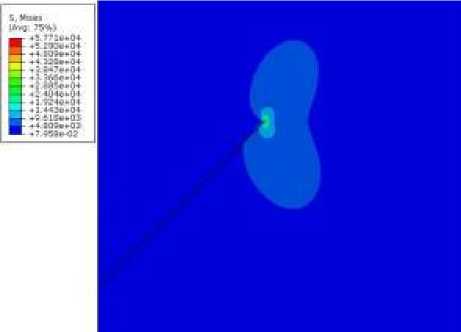
d
Me = 0,33
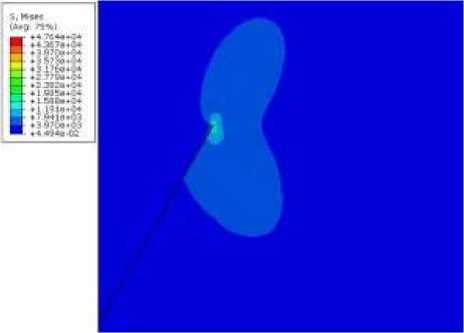
e
Me = 0,16

f
Рис. 8. Геометрия модели и распределение интенсивности касательных напряжений в окрестности вершины бокового выреза для различных параметров смешанности нагружения
Fig. 8. Geometry of the model and contours of the von Mises equivalent stress in the vicinity of the notch tip for different values of the mixity parameter
|
r / a |
° 11 |
O 22 |
0 12 |
|
0,5 |
z \ /wul ^ |
4 V 1 1 HIM I |
A 2LA___r V |
|
1 |
Xatn V f |
||
|
1,5 |
J НАЗА L |
A\ 4№,i / \ z / ..A A^.A .A^/^ |
|
|
3 |
™A ...... -^ f A U Л -...... 13 у |
||
|
6 |
Ln \ / V V \ |
/\1/Л 1 л л ti: |
A |
Truncated Williams series expansion FEM solution
Рис. 9. Угловые распределения компонент тензора напряжений в окрестности вершины трещины моды I для различных расстояний от вершины трещины. Черные точки соответствуют численному решению МКЭ. Красная линия показывает восстановленное асимптотическое разложение Уильямса (1) со слагаемыми более высокого порядка, где коэффициенты получены из результатов ПМ
Fig. 9. Circumferential distributions of the stress components in the vicinity of the Mode I notch tip at different distances from the notch tip.
Black points present numerical solution obtained by FEA. Red lines show the reconstructed asymptotic Williams solution (1) with the higher order terms whose coefficients are computed by ODM
Me = 0,16
Me = 0,33
Me = 0,5
Me = 0,66
^ 11
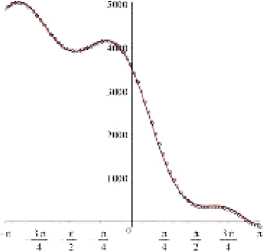
Truncated Williams series expansion FEM solution
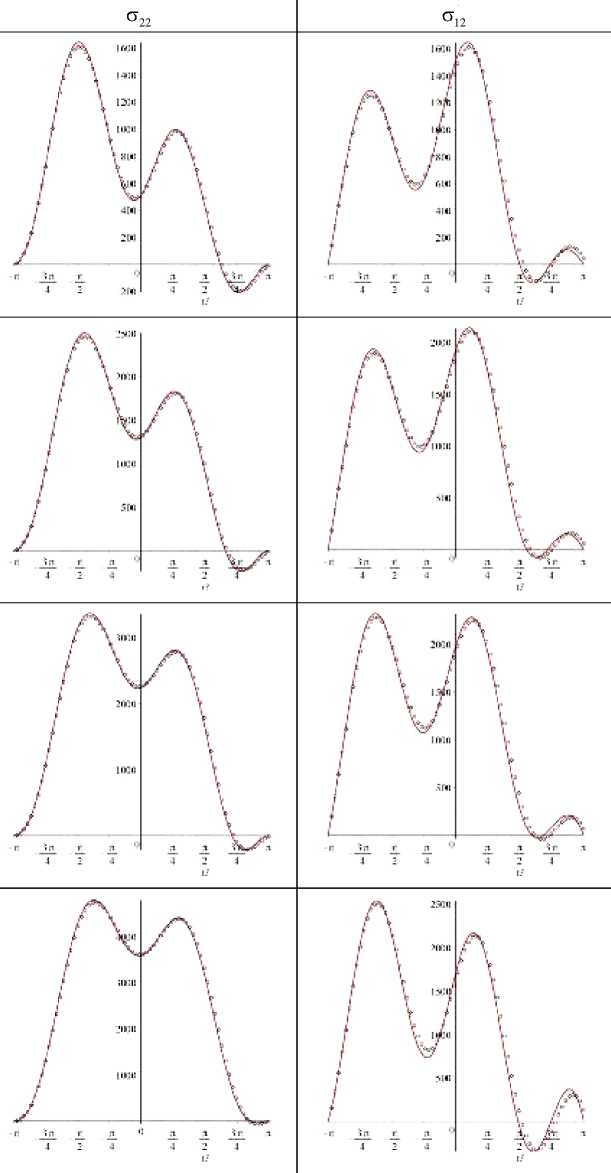
Рис. 10. Зависимости компонент тензора напряжений от полярного угла в окрестности вершины трещины для смешанных нагрузок при различных значениях параметрах смешанности при r / a = 1. Черные точки соответствуют численному решению МКЭ. Красная линия показывает восстановленное асимптотическое разложение Уильямса (1) со слагаемыми более высокого порядка, где коэффициенты получены из результатов ПМ
Fig. 10. Circumferential distributions of the stress components in the vicinity of the Mixed Mode notch tip for different values of the mixity parameter at r / a = 1. Black points present numerical solution obtained by FEA. Red lines show the reconstructed asymptotic Williams solution (1) with the higher order whose coefficients are computed by ODM
Коэффициенты разложения Уильямса, полученные с помощью ПМ, основанного на результатах МКЭ для смешанного деформирования, приведены в табл. 2–5.
4. Молекулярно-динамическое вычисление параметров классической механик и разрушения
В том, что следует ниже, воплощена процедура ПМ, основанная на моделировании методом МД. Получив распределения напряжений МД, показанные на рис. 3–
-
7, можно реализовать процедуру ПМ на основе решений МД и вычислить коэффициенты слагаемых более высокого порядка в ряде Уильямса (1).
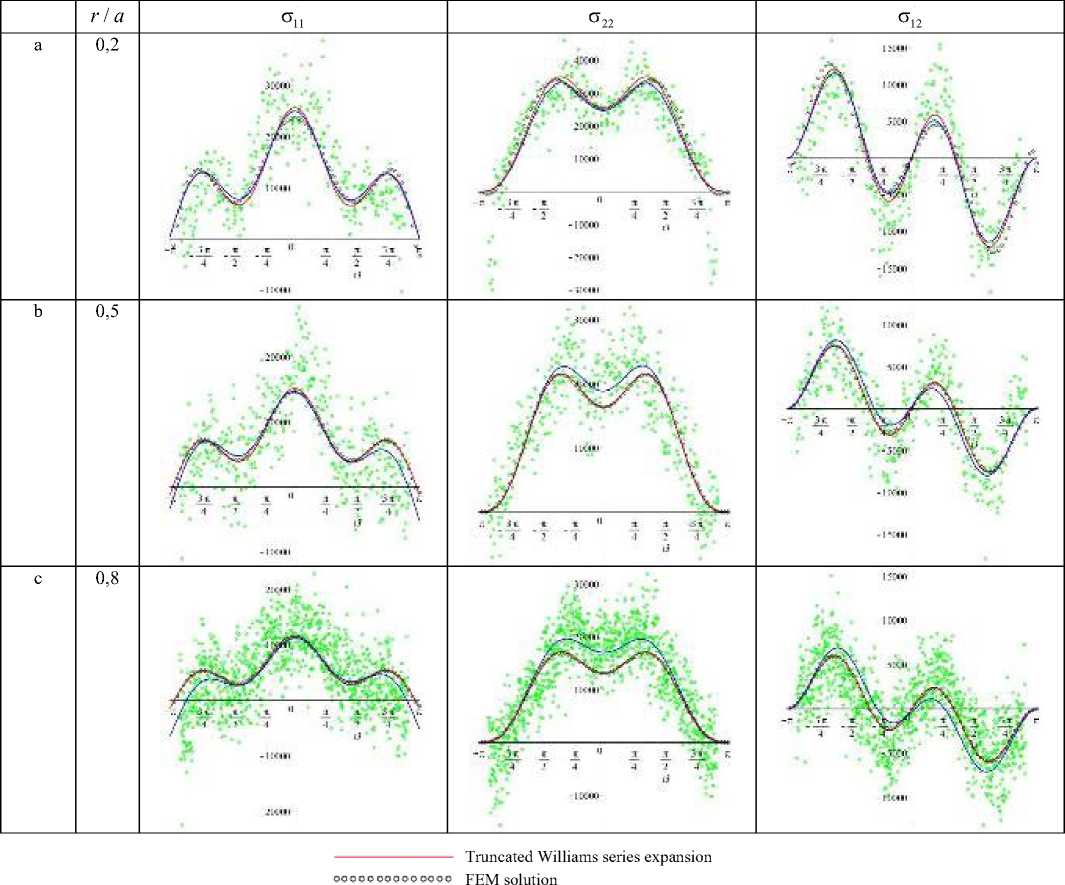
В расчетной схеме необходимы только атомистические напряжения и координаты атомов вокруг вершины трещины. Угловые распределения атомистических напряжений и сравнение асимптотического решения континуальной механики разрушения и распределений атомистических напряжений, полученных на разных расстояниях от вершины трещины, показаны на рис. 11 и 12.
The reconstructed Williams solution
Molecular dynamics solution
Рис. 11. Зависимости напряжений: а – от полярного угла для M e = 1 , полученные для кольцевой области с внутренним радиусом 7 Å, а внешним 15 Å; b – от полярного угла для M e = 1 , полученные для кольцевой области с внутренним радиусом 28 Å, а внешним 32 Å; c – от полярного угла для Me = 1 , полученные для кольцевой области с внутренним радиусом 49 Å, а внешним 55 Å
оо
Fig. 11. The angular distributions: a – of stresses for M e = 1 obtained for the ring area with the inner radius 7 A and the outer radius 15 A ;
оо b – of stresses for M e = 1 obtained for the ring area with the inner radius 28 A and the outer radius 32 A ; c – of stresses for M e = 1
оо obtained for the ring area with the inner radius 49 A and the outer radius 55 A
|
° 11 |
O 22 |
° 12 |
|
|
M e = = 0,16 |
KUKI im» Г\ Л\ 4 -2 ■ в 4 у 4V '-5000 ’/ . X । mm • . \ |
/ IKKI! i, 7" T 7 7 T 7" |
2мт ,1 яхй \. -г 1»!1 2 2^ 22 -‘^ т 4^4 4 2 *7Г -50011 |
|
M e = = 0,33 |
ж« ---;—/ ^422! .* ,л ° 2 2 1»^ / / ' 1 -IWM |
-л ;^л п л 5 л X Эл ’ .т т’ 4 ~ Л * 4 4 » 4 -|«юи L? амт |
мот Д V 4 2.4 4 У . 4 / ' -5000 ‘ \ "г* / •' imm |
|
Me = = 0,5 |
зтт 1 I KIWI \ 4 2 4 4 2 4 \ imm . a \ -2D0DU |
#»оп Д * э”»' ' : \ . 7. 2WW . V IMDQ П П Г 1 л X % Г ,1 * 2 1МИ1 7 -2MJWI мпт |
*1*2 а < <7 -tyi»i х / |
|
Me = = 0,66 |
моно / d .JL .2 " * x- u V /*4*24 4 4/4 1 |
Я» DO ' 4 " 2 4 Т Т |
атм / ||«|« \ д 2 ху 4 у 7 -2ММ |
The reconstructed Williams solution
Molecular dynamics solution
Рис. 12. Зависимости напряжений от полярного угла для Me = 0,16; Me = 0,33; Me = 0,5 и Me = 0,66, полученные для кольцевой области с внутренним радиусом 28 Å, а внешним 32 Å
Fig. 12. The angular distributions of stresses for Me = 0.16 ; Me = 0.33 ; Me =0.5 and Me = 0.66 obtained for the ring area о о with the inner radius 28 A and the outer radius 32 A
Рисунок 11 иллюстрирует окружные распределения компонент тензора напряжений, полученные с помощью моделирования МД (зеленые точки), решения МКЭ (черные круги), восстановленные решения ряда из МКЭ (красные линии) и восстановленное асимптотическое поле напряжений на основе моделирования МД (синие линии). Здесь r / a – безразмерное расстояние от вершины трещины. Можно еще раз отметить, что синяя линия показывает распределение, основанное на усеченном разложении ряда Уильямса (1), в котором сохраняются пятнадцать коэффициентов, полученных ПМ из моделирования МД. Черные точки, показывающие распределения МКЭ, и красные линии, показывающие реконструированное разложение Уильямса из конечноэлементного анализа, являются теми же точками, которые показаны на рис. 9. Можно видеть, что красные и синие линии, изображающие усеченное расширение приближенного ряда, расположены очень близко друг к другу. Выявленные закономерности действительны для разных расстояний от кончика надреза. На рис. 12 показаны угловые распределения компонент тензора напряжений для различных значений параметра смешанности. Первая строка показывает зависимости напряжений от полярного угла для M e = 0,16, вторая строка показывает зависимости компонент тензора напряжений от полярного угла для M e = 0,33 , третья строка показывает зависимости компонент тензора напряжений для M e = 0,5, четвертая строка показывает зависимости компонент тензора напряжений от полярного угла для M e = 0,66 при 20 пс. Найдено хорошее соответствие между атомистическими и механическими полями напряжений сплошной среды. Во всех случаях сплошные и атомистические распределения напряжений по окружности демонстрируют одинаковое качественное поведение при всех значениях полярного угла. Стоит отметить, что напряжения в атомистическом моделировании вычисляют в соответствии со следующей формулой
N
3 j
= (1/ V ) £ (1/2) £ ( г "
р L а = 1
- г р) f Г - тм ij ij
где i , j – индексы декартовой системы координат и принимают значения 1, 2 и 3, V - это общий объем, а изменяет значения от 1 до N и равно номеру соседнего атома р, г р положение атома р вдоль направления i , fj" - это сила (вдоль направления j ) с которой атом а действует на атом р , т р - это масса атома р и v p -скорость теплового возмущения атома р . Это слагаемое однозначно определено только для парных потенциалов и потенциалов внедренного атома. Вириальные напряжения, вычисленные на основе моделирования молекулярной динамики, должны быть усреднены по времени, чтобы быть эквивалентным континуальному тензору напряжений Коши [33].
Вычисленные значения коэффициентов слагаемых более высокого порядка в асимптотическом разложении Уильямса ak1 и ak2 , полученные с помощью ПМ, приведены в табл. 1–5. Можно наблюдать поразительно хорошее соответствие между коэффициентами, полученными с помощью молекулярно-динамического моделирования и посредством континуального подхода ЛМР. Для отражения изменения коэффициентов разложения Уильямса ak1 и ak2 с изменением параметра смешанности M e целесообразно ввести безразмерные коэффициенты разложения Уильямса согласно формулам к/2-1
11a a = at------^, к к _a> 2 ’
322 cos у
a k 2
k /2-1
2 a
= a к ”-----■----
3^2 sin у cosy
где а - это длина надреза, 3^2 - приложенная нагрузка. Затем удобно перейти к нормированным коэффициентам ak2 =
ak 2
(a^^T^^
( a 1 ) 2 + ( a 2 ) 2
Таким образом, в соответствии с формулами (17) и (18) коэффициенты ak 1 и ak 2 нормируются с помощью значений коэффициентов лидирующих слагаемых в (1). Нормированные коэффициенты ak 1 и ak 2 приведены в табл. 1–5. В табл. 2–5 представлены коэффициенты ak 1 и ak 2 для четырех различных значений параметра смешанности нагружения, полученные с помощью двух подходов. Можно видеть, что КИН и T-напряжения могут быть вычислены с высокой точностью, тогда как расхождения в коэффициентах более высокого порядка разложения Уильямса увеличиваются с увеличением индекса коэффициента для всех значений параметра смешанности. Тем не менее установлено хорошее соответствие между результатами моделирования МД и результатами МКЭ.
Поле напряжений в окрестности вершины трещины нормального отрыва определяется только коэффициентами a k 1 (см. табл. 1). В этом случае все коэффициенты a k 2 равны нулю, в то время как для моды II все коэффициенты a k 1 равны нулю и поле вблизи вершины трещины описывается исключительно коэффициентами a k 2 . С уменьшением параметра смешанности M e от 1 до нуля нормированные коэффициенты a 11 уменьшаются, а коэффициенты a 12 увеличиваются по абсолютному значению. В табл. 1 показаны нормированные коэффициенты разложения Уильямса, полученные с помощью МД-моделирования (вторая колонка) и МКЭ (третья колонка). Коэффициенты a 11 , полученные при использовании двух подходов, равны друг другу с точностью не менее пяти знаков после запятой.
Разница между коэффициентами a 115 , вычисленными с использованием двух подходов, составляет менее 9 %. Таким образом, можно заметить, что чем выше индекс коэффициента, тем больше ошибка.
Из табл. 1–5 видно, что КИН, T-напряжения и коэффициенты a31 и a32 для всех значений параметра смешанности надежно вычисляются с высокой точностью. Погрешность увеличивается с возрастанием порядкового номера коэффициента. Чем больше число коэффициентов, тем больше ошибка в вычисленных коэффициентах. Но для других коэффициентов с более высокими порядковыми номерами погрешность не превышает десяти процентов.
Таблица 1
Вычисленные значения коэффициентов более высокого порядка разложения Уильямса поля напряжений в окрестности вершины трещины, нормальный отрыв
Table 1
The computed values of the higher order coefficients of the Williams series expansion for the stress field in the vicinity of the crack tip, Mode I loading
|
Нормированные коэффициенты разложения Уильямса, мода I |
Нормированные коэффициенты разложения Уильямса, метод МД |
Нормированные коэффициенты разложения Уильямса, МКЭ |
Различие между МД моделированием и МКЭ |
|
a 1 1 |
1,000000 |
1,000000 |
0 % |
|
a 2 1 |
-0,156644 |
-0,156644 |
0 % |
|
a 3 1 |
0,122136 |
0,122997 |
0,7 % |
|
a 4 1 |
-0,089284 |
-0,090369 |
1,2 % |
|
a 5 1 |
0,012002 |
0,012235 |
1,9 % |
|
a 6 1 |
0,008880 |
0,009108 |
2,5 % |
|
a 7 1 |
-0,007128 |
-0,007341 |
2,9 % |
|
a 8 1 |
-0,006428 |
-0,006647 |
3,3 % |
|
a 9 1 |
0,004396 |
0,004567 |
3,8 % |
|
a 10 |
0,001376 |
0,001435 |
4,1 % |
|
a 11 |
-0,001002 |
-0,001051 |
4,6 % |
|
a 1 1 2 |
0,000830 |
0,000880 |
5,3 % |
|
a 13 |
0,000269 |
0,000286 |
5,8 % |
|
a 1 1 4 |
-0,000580 |
-0,000626 |
7,4 % |
|
a 15 |
-0,000172 |
-0,000189 |
8,7 % |
Таблица 2
Вычисленные значения коэффициентов более высокого порядка разложения Уильямса поля напряжений в окрестности вершины трещины, смешанное нагружение, параметр смешанности M e = 0,66
Table 2
The computed values of the higher order coefficients of the Williams series expansion for the stress field in the vicinity of the crack tip, Mixed Mode loading, M e = 0,66
|
Нормированные коэффициенты разложения Уильямса, мода I |
Нормированные коэффициенты разложения Уильямса, метод МД |
Нормированные коэффициенты разложения Уильямса, МКЭ |
Разница между МД-моделированием и МКЭ, % |
Нормированные коэффициенты разложения Уильямса, мода II |
Нормированные коэффициенты разложения Уильямса, метод МД |
Нормированные коэффициенты разложения Уильямса, МКЭ |
Разница между МД-моделированием и МКЭ, % |
|
a 1 1 |
0,951104 |
0,951104 |
0 |
a 1 2 |
-0,308872 |
-0,308872 |
0 |
|
a 2 1 |
-0,034953 |
-0,034953 |
0 |
a 2 2 |
0 |
0 |
0 |
|
a 3 |
0,003690 |
0,003690 |
0 |
2 a 32 |
-0,159587 |
-0,159587 |
0 |
|
a 41 |
-0,043062 |
-0,043279 |
0.5 |
2 a 42 |
0,103658 |
0,103970 |
0,3 |
Окончание табл. 2
|
Нормированные коэффициенты разложения Уильямса, мода I |
Нормированные коэффициенты разложения Уильямса, метод МД |
Нормированные коэффициенты разложения Уильямса, МКЭ |
Разница между МД-моделированием и МКЭ, % |
Нормированные коэффициенты разложения Уильямса, мода II |
Нормированные коэффициенты разложения Уильямса, метод МД |
Нормированные коэффициенты разложения Уильямса, МКЭ |
Разница между МД-моделированием и МКЭ, % |
|
a 5 1 |
0,051488 |
0,052273 |
1,5 |
2 a 5 2 |
0,018770 |
0,018884 |
0,6 |
|
a 6 |
0,0037369 |
-0,003821 |
2,2 |
2 a 6 2 |
0,050030 |
-0,050383 |
0,7 |
|
a 7 1 |
-0,002251 |
-0,002319 |
2,9 |
a 7 2 |
0,011338 |
0,011441 |
0,9 |
|
a 1 8 |
0,001913 |
0,001976 |
3,2 |
a 2 8 |
0,009921 |
0,010032 |
1,1 |
|
a 9 |
-0,001671 |
-0,001732 |
3,5 |
2 a 9 2 |
0,008254 |
-0,008354 |
1,2 |
|
a 10 |
-0,000928 |
-0,000965 |
3,8 |
2 a 10 |
0,003273 |
0,003347 |
2,2 |
|
a 11 |
0,000768 |
0,000802 |
4,2 |
a 121 |
0,002877 |
0,002966 |
3,0 |
|
a 112 |
0,000620 |
0,000651 |
4,8 |
a 122 |
-0,001746 |
-0,001821 |
4,1 |
|
a 13 |
-0,000385 |
-0,000407 |
5,5 |
2 a 123 |
-0,000885 |
-0,000934 |
5,2 |
|
a 14 |
0,000209 |
0,000225 |
6,7 |
2 a 124 |
0,000347 |
0,000369 |
5,9 |
|
a 15 |
0,000038 |
0,000041 |
8,0 |
2 a 125 |
-0,000025 |
-0,000027 |
6,7 |
Таблица 3
Вычисленные значения коэффициентов более высокого порядка разложения Уильямса поля напряжений в окрестности вершины трещины, смешанное нагружение, параметр смешанности M e = 0,5
Table 3
The computed values of the higher order coefficients of the Williams series expansion for the stress field in the vicinity of the crack tip, Mixed Mode loading, Me = 0,5
|
Нормированные коэффициенты разложения Уильямса, мода I |
Нормированные коэффициенты разложения Уильямса, метод МД |
Нормированные коэффициенты разложения Уильямса, МКЭ |
Разница между МД-моделиро-ванием и МКЭ, % |
Нормированные коэффициенты разложения Уильямса, мода II |
Нормированные коэффициенты разложения Уильямса, метод МД |
Нормированные коэффициенты разложения Уильямса, МКЭ |
Разница между МД-модели-рованием и МКЭ, % |
|
a 1 1 |
0,892768 |
0,892768 |
0 |
2 a 1 |
-0,450517 |
-0,450517 |
0 |
|
a 2 1 |
0,134018 |
0,134018 |
0 |
2 a 2 |
0 |
0 |
0 |
|
a 3 1 |
-0,098480 |
-0,098598 |
0,12 |
a 3 2 |
-0,226138 |
-0,226138 |
0 |
|
a 4 1 |
-0,021063 |
-0,021093 |
0,14 |
a 4 2 |
0,199294 |
0,199493 |
0,1 |
|
a 5 1 |
0,106156 |
0,106337 |
0,17 |
2 a 5 |
0,113325 |
0,113552 |
0,2 |
|
a 6 1 |
-0,039648 |
-0,039787 |
0,35 |
a 6 2 |
-0,078524 |
-0,078760 |
0,3 |
|
a 7 1 |
-0,013781 |
-0,013891 |
0,79 |
a 7 2 |
0,039687 |
0,039887 |
0,5 |
|
a 8 |
0,010634 |
0,010752 |
1,1 |
2 a 8 2 |
-0,008410 |
-0,008513 |
1,2 |
|
a 9 |
-0,009644 |
-0,009831 |
1,9 |
2 a 92 |
-0,045587 |
-0,024666 |
2,3 |
|
a 10 |
-0,006739 |
-0,006926 |
2,7 |
2 a 10 |
0,016783 |
0,017231 |
2,6 |
|
a 111 |
0,004748 |
0,005003 |
5,1 |
a 121 |
-0,008256 |
-0,008529 |
3,2 |
|
a 12 |
-0,004587 |
-0,004854 |
5,5 |
a 122 |
-0,006994 |
-0,007324 |
4,5 |
|
a 13 |
-0,003402 |
-0,003627 |
6,2 |
a 123 |
0,003252 |
0,0034471 |
6,3 |
|
a 14 |
0,002291 |
0,002471 |
7,3 |
a 124 |
-0,000991 |
-0,001068 |
7,2 |
|
a 15 |
-0,000799 |
-0,000882 |
9,4 |
a 125 |
0,000233 |
0,000254 |
8,1 |
Таблица 4
Вычисленные значения коэффициентов более высокого порядка разложения Уильямса поля напряжений в окрестности вершины трещины, параметр смешанности Me = 0,33
The computed values of the higher order coefficients of the Williams series expansion for the stress field in the vicinity of the crack tip, Mixed Mode loading, M e = 0.33
Table 4
|
Нормированные коэффициенты разложения Уильямса, мода I |
Нормированные коэффициенты разложения Уильямса, метод МД |
Нормированные коэффициенты разложения Уильямса, МКЭ |
Разница между МД-моделированием и МКЭ, % |
Нормированные коэффициенты разложения Уильямса, мода II |
Нормированные коэффициенты разложения Уильямса, метод МД |
Нормированные коэффициенты разложения Уильямса, МКЭ |
Разница между МД-моделированием и МКЭ, % |
|
a 11 |
0,811486 |
0,811486 |
0 |
a 12 |
-0,584370 |
-0,584370 |
0 |
|
a 21 |
0,423408 |
0,423408 |
0 |
a 22 |
0 |
0 |
0 |
|
a 31 |
-0,373289 |
-0,373663 |
0,1 |
a 32 |
-0,258031 |
-0,258289 |
0,1 |
|
a 41 |
0,278854 |
0,279413 |
0,2 |
a 42 |
0,103880 |
0,104099 |
0,21 |
|
a 51 |
0,229121 |
0,229810 |
0,3 |
a 52 |
-0,094738 |
-0,094966 |
0,24 |
|
a 61 |
-0,174783 |
-0,175838 |
0,6 |
a 62 |
0,073484 |
-0,073713 |
0,31 |
|
a 7 |
0,118878 |
0,120322 |
1,2 |
a 72 |
0,064157 |
0,064421 |
0,41 |
|
a 81 |
0,108276 |
0,109925 |
1,5 |
a 82 |
-0,049189 |
-0,049837 |
1,3 |
|
a 9 1 |
-0,008786 |
-0,008947 |
1,8 |
a 9 2 |
0,028069 |
0,0286711 |
2,1 |
|
a 110 |
0,007147 |
0,007301 |
2,1 |
a 120 |
0,014809 |
0,015299 |
3,2 |
|
a 111 |
0,005064 |
0,005286 |
4,2 |
a 121 |
-0,008819 |
-0,009225 |
4,4 |
|
a 112 |
-0,003737 |
-0,003951 |
5,4 |
2 a 12 |
0,007624 |
0,008034 |
5,1 |
|
a 113 |
0,001871 |
0,002012 |
7,0 |
a 123 |
0,005762 |
0,006236 |
7,6 |
|
a 14 |
-0,000920 |
-0,001001 |
8,0 |
a 124 |
-0,003931 |
-0,004291 |
8,4 |
|
a 115 |
-0,004203 |
-0,000466 |
9,8 |
a 125 |
-0,000925 |
-0,001025 |
9,8 |
Таблица 5
Вычисленные значения коэффициентов более высокого порядка разложения Уильямса поля напряжений, параметр смешанности M e = 0,16
The computed values of the higher order coefficients of the Williams series expansion for the stress field, Mixed Mode loading, Me = 0.16
Table 5
|
Нормированные коэффициенты разложения Уильямса, мода I |
Нормированные коэффициенты разложения Уильямса, метод МД |
Нормированные коэффициенты разложения Уильямса, МКЭ |
Разница между МД-моделиро-ванием и МКЭ, % |
Нормированные коэффициенты разложения Уильямса, мода II |
Нормированные коэффициенты разложения Уильямса, метод МД |
Нормированные коэффициенты разложения Уильямса, МКЭ |
Разница между МД-моде-лированием и МКЭ, % |
|
a 1 1 |
0,713306 |
0,713306 |
0 |
a 1 2 |
-0,700852 |
-0,700852 |
0 |
|
a 2 1 |
0,998023 |
0,998023 |
0 |
a 2 2 |
0 |
0 |
|
|
a 3 1 |
-1,126277 |
-1,126277 |
0 |
a 3 2 |
-0,173304 |
-0,173304 |
0 |
|
a 4 1 |
0,306639 |
0,306946 |
0,1 |
a 4 2 |
0,147978 |
0,148722 |
0,5 |
|
a 5 1 |
0,210141 |
0,210773 |
0,3 |
2 a 5 2 |
-0,134715 |
-0,137324 |
1,9 |
|
a 6 |
-0,105048 |
-0,106002 |
0,9 |
2 a 62 |
-0,113041 |
-0,115466 |
2,1 |
|
a 7 1 |
0,007485 |
0,007599 |
1,5 |
2 a 7 2 |
0,104874 |
0,107784 |
2,7 |
|
a 1 8 |
0,004900 |
0,005021 |
2,4 |
2 a 2 8 |
-0,008972 |
-0,009288 |
3,4 |
|
a 9 |
-0,003650 |
-0,003822 |
4,5 |
2 a 9 2 |
0,007892 |
0,008325 |
5,2 |
|
a 110 |
0,001716 |
0,001804 |
4,9 |
2 a 10 |
0,007262 |
0,007718 |
5,9 |
Окончание табл. 5
|
Нормированные коэффициенты разложения Уильямса, мода I |
Нормированные коэффициенты разложения Уильямса, метод МД |
Нормированные коэффициенты разложения Уильямса, МКЭ |
Разница между МД-моделиро-ванием и МКЭ, % |
Нормированные коэффициенты разложения Уильямса, мода II |
Нормированные коэффициенты разложения Уильямса, метод МД |
Нормированные коэффициенты разложения Уильямса, МКЭ |
Разница между МД-моде-лированием и МКЭ, % |
|
a 11 |
0,001209 |
0,001282 |
5,7 |
^ 11 |
-0,006027 |
-0,006439 |
6,4 |
|
a 12 |
-0,000885 |
-0,000944 |
6,2 |
a 2 |
0,005066 |
0,005447 |
7,0 |
|
a 113 |
0,000805 |
0,000865 |
6,9 |
a 123 |
0,001673 |
0,001815 |
7,8 |
|
a 14 |
-0,000663 |
-0,000721 |
8,1 |
a 2 |
-0,000886 |
-0,000965 |
8,5 |
|
a 15 |
0,000391 |
-0,000434 |
9,8 |
a 2 |
-0,000715 |
-0,000794 |
9,9 |
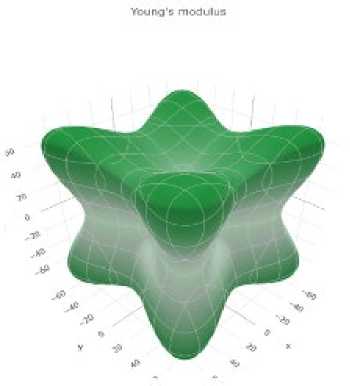
Рис. 13. Визуализация упругих свойств материала, обладающего кубической симметрией: модуль Юнга и коэффициент Пуассона кристалла алюминия

Fig. 13.Visualisation of elastic properties of a material with cubic symmetry: Young’s modulus and Poisson’s ration of single-crystal aluminum
5. Сравнение результатовдля монокристаллических меди и алюминия
Для получения более общих выводов о возможности применения подходов классической линейной механики разрушения на наноскопическом масштабе были выполнены аналогичные расчеты в многофункциональном и многоцелевом комплексе Simulia abaqus и в пакете, реализующем МД, LAMMPS для монокристаллического ГЦК алюминия. Для МД-расчетов был использован потенциал внедренного атома Al_inp.eam. Сначала были найдены упругие свойства кристалла. Матрица упругих модулей монокристаллического алюминия имеет вид (в ГПа):
|
' 107,25 |
81, 44 |
81, 44 |
0 |
0 |
0 ) |
|
81,44 |
107, 25 |
81, 44 |
0 |
0 |
0 |
|
81,44 |
81,84 |
107, 25 |
0 |
0 |
0 |
|
0 |
0 |
0 |
46,16 |
0 |
0 |
|
0 |
0 |
0 |
0 |
46,16 |
0 |
|
. 0 |
0 |
0 |
0 |
0 |
46,16 , |
Модуль Юнга имеет пространственную интерпретацию, представленную на рис. 13. Результаты МД-расчетов для алюминия и сопоставление результатов для меди и алюминия приведены на рис. 14 и 15.
Из представленных распределений видно, что картины деформирования пластин с боковым вырезом в целом не зависят от выбранных материалов (безусловно, принадлежащих к одному классу сингоний). Поэтому можно заключить, что полученные картины компонент тензора напряжений подобны распределениям классической механики разрушения, и атомистические поля напряжений могут быть использованы для вычисления макроскопических параметров механики разрушения, и, наоборот, имеющие оценки макроскопических параметров могут быть использованы для характеристики атомистических распределений.
Заключение
Найдены значения КИН, T-напряжения и коэффициенты слагаемых более высокого порядка в разложении Уильямса для полей напряжений вблизи вершины бокового надреза в медной пластине при нормальном от- рыве и смешанных типах нагружения для различных значений параметра смешанности с помощью МД-модели-рования. С помощью атомистических координат выбранных точек и атомистических напряжениях вблизи вершины надреза определены амплитудные коэффициенты многопараметрического разложения Уильямса континуальной ЛМР.
Новизна подхода заключается в вычислении коэффициентов слагаемых более высокого порядка в разложении Уильямса классической механики разрушения. Вычислительные эксперименты, выполненные в гибком инструменте моделирования LAMMPS, наглядно демонстрируют возможность надежного вычисления коэффициентов более высокого порядка. Как показано в табл. 1–5, чем больше индекс коэффициента, тем больше разница между МД и конечно-элементным решением. Стоит отметить, что полученные пятнадцать коэффициентов показывают, что атомистическое поле напряжений может быть точно описано многопараметрическим разложением Уильямса. Проведено сравнение полей напряжений у вершины надреза, полученных в результате атомистического моделирования и теории разрушения механики сплошных сред. Тщательное атомистическое моделирование показывает, что механика сплошной среды может быть успешно применена на наноуровне. Наблюдается хорошее соответствие между напряжениями на обоих уровнях описания. Показана актуальность традиционной ЛМР в нанометровом диапазоне для упругого режима деформирования.
Полученное разложение в ряд поля напряжений в окрестности вершины надреза может быть полезно для построения многомасштабных моделей разрушения, объединяющих процессы и явления на макро-, мезо- и наноуровнях [62–64]. В настоящее время складывается позиция, что крайне важно и естественно разрабатывать многомасштабные и иерархические модели, а сочетание подхода механики сплошных сред и атомистического моделирования позволяет нам получить более глубокое понимание и реалистичное описание поведения роста трещин и процесса деформации при различных системах сложных нагрузок. Такой подход открывает широкие перспективы для описания процессов разрушения на различных масштабных уровнях, а именно в больших пространственных и временных масштабах.
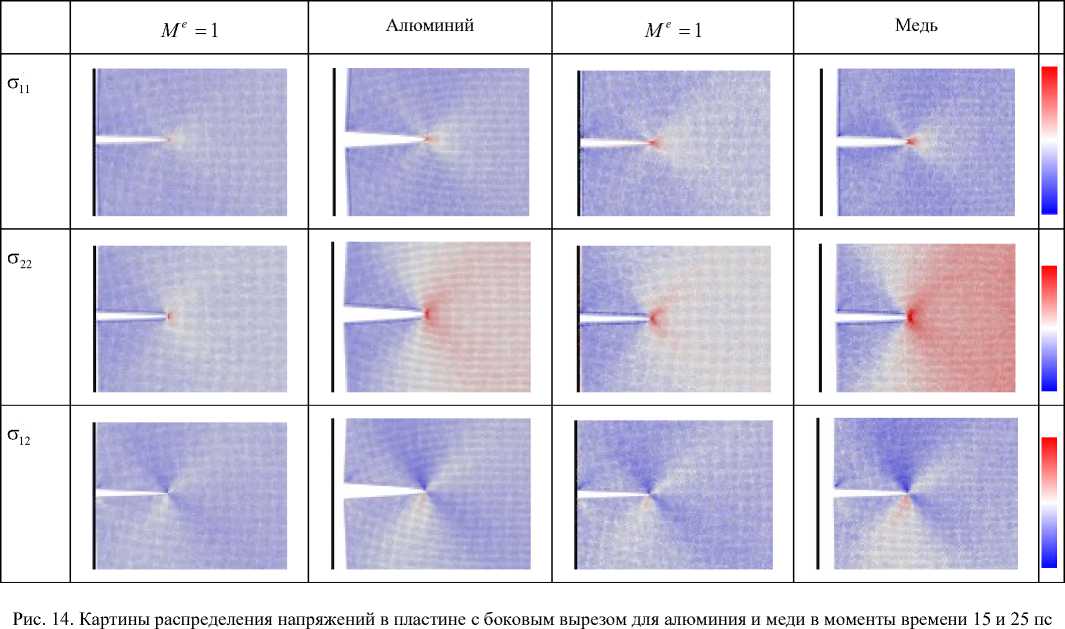
Fig. 14. The stress morphology and the stress components for the mixity parameter M e = 1 at 15 and 25 ps
|
Me = 0,16 |
Алюминий |
Me = 0,16 |
Медь |
||
|
° 11 |
■м |
1 г1 1. | -7БГПа |
|||
|
О 22 |
I IKt Ша 75 ГПа |
||||
|
О 12 |
। 75 ГП* । -i^’L На |
Рис. 15. Картины распределения напряжений в пластине с боковым вырезом для алюминия и меди 15 и 25 пс
Fig. 15. The stress morphology and the stress components for the mixity parameter Me = 0.16 at 15 and 25 ps
Список литературы Идентификация коэффициентов интенсивности напряжений, T-напряжений и коэффициентов регулярных слагаемых высокого порядка в разложении Уильямса с помощью молекулярно-динамического моделирования
- Ritchie R.O., Liu D. Introduction to fracture mechanics // Elsevier, 2021.
- Breakdown of Continuum Fracture Mechanics at the Na-noscale / T. Shimada, K. Ouchi, Y. Chihara, T. Kitamura // Sci Rep. - 2015. - № 8596. DOI: 10.1038/srep08596
- Hello G. Derivation of complete crack-tip stress expansions from Westergaard-Sanford solutions // International Journal of Solids and Structures. - 2018. - Vol. 144-145. - Р. 265-275. DOI: 10.1016/j.ijsolstr.2018.05.012
- Karihaloo B.L., Xiao Q.Z. Accurate determination of the coefficients of elastic crack tip asymptotic field by a hybrid crack element with p-adaptivity // Engineering Fracture Mechanics. -2001. - Vol. 68, no. 15. - P. 1609-1630. DOI: 10.1016/S0013-7944(01)00063-7
- Benito deCelis, Argon Ali S. Molecular dynamics simulation of crack tip processes in alpha-iron and copper // Journal of Applied Physics. - 1983. - Vol. 54. - P. 4864. DOI: 10.1063/1.332796.
- Buehler M.J., Gao H.J., Huang Y. Atomistic and continuum studies of stress and strain fields near a rapidly propagating crack in a harmonic lattice // Theoretical and Applied Fracture Mechanics. - 2004 - Vol. 41. - Р. 21-42. DOI: 10.1016/j .tafmec .2003.11.022
- Cheng S.H., Sun C.T. Applicability of continuum fracture mechanics in atomistic systems // Proc. ASME. IMECE2011. -2011. - № 8. - Р. 283-288. DOI: 10.1115/IMECE2011-63478
- Wilson M.A., Grutzik S.J., Chandross M. Continuum stress intensity factors from atomistic fracture simulations // Com-put. Methods Appl. Mech. Engrg. - 2019. - No. 354. -P. 732-749. DOI: 10.1016/j.cma.2019.05.050
- Roy S., Roy A. A computational investigation of length-scale effects in the fracture behaviour of a graphene sheet using the atomistic J-integral // Engineering Fracture Mechanics. -2019. - No. 207. - P. 165-180. DOI: 10.1016/j.engfracmech.2018.12.012
- Tsai J.-L., Tzeng S.-H., Tzou Y.-J. Characterizing the fracture parameters of a graphene sheet using atomistic simulation and continuum mechanics // International Journal of Solids and Structures. - 2010. - No. 47. - P. 503-509. DOI: 10.1016/j. ij solstr.2009.10.017
- Jin Y., Yuan F.G. Nanoscopic modelling of fracture of 2D graphene systems // Journal of Nanoscience and Nanotechnol-ogy. - 2005. - Vol. 5, no. 4. - P. 601-608. DOI: 10.1166/jnn.2005.071
- Crack front propagation and fracture in a graphene sheet: a molecular-dynamics study on parallel computers / A. Omel-tchenko, J. Yu, R.K. Kalia, P. Vashishta // Physical Review Letters. - 1997. - Vol. 78. - P. 2148-2151. DOI: 10.1103/PhysRevLett.78.2148
- Mechanical responses of pristine and defective C3N nanosheets studied by molecular dynamics simulations / A.H.N. Shirazi, R. Abadi, M. Izadifar, N. Alajlan, T. Rabczuk // Computational Materials Science. - 2018. - Vol. 147. - P. 316-321. DOI: 10.1016/j.commatsci.2018.01.058
- Fracture toughness and crack propagation behavior of nanoscale beryllium oxide graphene-like structures: A molecular dynamics simulation analysis / M.Z. Dehaghani, A.H. Mashha-dzadeh, A. Salmankhani, Z. Karami, S. Habibzadeh, M.R. Ganjali, M.R. Saeb // Engineering Fracture Mechanics. - 2020. - Vol. 235. -P. 107194. DOI: 10.1016/j.engfracmech.2020.107194
- Fracture mechanics of polycrystalline beryllium oxide nanosheets: A theoretical basis / M.Z. Dehaghani A., Salmankhani, A.H. Mashhadzadeh, S. Habibzadeh, O. Abida, M.R. Saeb // Engineering Fracture Mechanics. - 2021. - Vol. 244. - P. 107552. DOI: 10.1016/j. engfracmech.2021.107552
- Fracture behavior of SiGe nanosheets: Mechanics of monocrystalline vs. polycrystalline structure / M.Z. Dehaghani, M.E. Safa, F. Yousefi, A. Salmankhani Z., Karami, A. Dadrasi, A.H. Mashhadzadeh, F.J. Stadler, M.R. Saeb // Engineering Fracture Mechanics. - 2021. - Vol. 251. - P. 107782. DOI: 10.1016/j .engfracmech.2021.107782
- Theoretical examination of the fracture behavior of BC3 polycrystalline nanosheets: Effect of crack size and temperature / A. Dadrasi, A. Albooyeh, S. Fooladpanjeh, A. Salmankhani, A.H. Mashhadzadeh, M.R. Saeb // Mechanics of Materials. - 2022. -Vol. 165. - P. 104158. DOI: 10.1016/j.mechmat.2021.104158
- A theoretical insight into the fracture behavior of the edge-cracked polycrystalline BC3 polycrystalline nanosheets / A. Dadrasi, S. Fooladpanjeh, A. Albooyeh A., Salmankhani, A.H. Mashhadzadeh, M.R. Saeb // Computational Materials Science. - 2021. -Vol. 192. - P. 110345. DOI: 10.1016/j.commatsci.2021.110345
- Applying molecular dynamics simulation to take the fingerprint of polycrystalline SiC nanosheets / F. Molaei, M.Z. Dehaghani, A. Salmankhani, S. Fooladpanjeh, S.M. Sajadi, M.E. Safa, O. Abida, S. Habibzadeh, A.H. Mashhadzadeh, M.R. Saeb // Computational Materials Science. - 2021. -Vol. 200. - P. 110770. DOI: 10.1016/j.commatsci.2021.110770
- Molaei F. Molecular dynamics simulation of edge crack in single crystalline alpha quartz // Journal of Molecular Graphics and Modelling. - 2022. - Vol. 111. - P. 108085. DOI: 10/1016/j.jmgm.2021.108085
- Fracture Toughness Estimation of Single-crystal Aluminum at Nanoscale / W. Velilla-Diaz, L. Ricardo, A. Palencia, H.R. Zambrano // Nanomaterials. - 2021. - Vol. 11, no. 3. -P. 689. DOI: 10.3390/nano11030680
- Le M.-Q. Molecular dynamics study of the fracture of single layer buckled silicon monosulfide and germanium selenide // Archives of mechanics. - 2022. - Vol. 74. - P. 1-10. DOI: 10.244423/aom.3871
- Nguen H.-T., Le M.-Q., Nguen V.-T. Mode-I stress intensity factors of silicene, AIN, and SiC hexagonal sheets // Material Research Express. - 2018. - Vol. 5, no. 6. - P. 065025. DOI: 10.1088/2053-1591/aac807
- A coupled/continuum study of graphene fracture / M. Xu, A. Tabarraei, J.T. Paci, J. Oswald, T. Belytschko // International Journal of Fracture. - 2012. - Vol. 173. - P. 163-173. DOI: 10.1007/s10704-011 -9675-x
- Le M.Q., Batra R.C. Mode-I stress intensity factor in single layer graphene sheets // Computational Materials Science. -2016. - Vol. 118. - P. 251-258. DOI: 10.1016/j.commatsci.2016.03.027
- Gallo P. Some Considerations on Stress Intensity Factor at Atomic Scale // In: Gdoutos E., Konsta-Gdoutos M. (eds) Proceedings of the Third International Conference on Theoretical, Applied and Experimental Mechanics. ICTAEM 2020. Structural Integrity. - 2020. - No. 16. DOI: 10.1007/978-3-030-47883-4_57
- Mai N.T., Choi S.T. Atomic-scale mutual integrals for mixed-mode fracture: Abnormal fracture toughness of grain boundaries in graphene // International Journal of Solids and Structures. -2018. - No. 138. - P. 205-216. DOI: 10.1016/j.ijsolstr.2018.01.013
- Stepanova L.V., Bronnikov S.A. Molecular Dynamics Modeling of Crack Propagation // Journal of Physics: Conference Series. - 2019. - Vol. 1368, no. 4. - P. 042039. DOI: 10.1088/1742-6596/1368/4/042039
- Stepanova L.V., Bronnikov S.A. Computational study of the mixed-mode crack behavior by molecular dynamics method and the multi-parameter crack field description of classical fracture mechanics // Theoretical and Applied Fracture Mechanics. -2020. - No. 109. - P. 102691. DOI: 10.1016/j.tafmec.2020.102691
- Stepanova L., Belova O. Stress intensity factors of Continuum fracture mechanics at the nanoscale // Procedia Structural Integrity. - 2022. - Vol. 37. - P. 900-907.
- Stepanova L.V., Belova O.N. A molecular dynamics simulation analysis of mixed mode crack growth // AIP Conference Proceedings. - 2021. - No. 2371. - P. 020012. DOI: 10.1063/5.0059574.
- Chen Z., Wang H., Liu G.-R. Fatigue crack propagation in carbon steel using RVE based model. - 2021. arXiv:2103.15399v1.
- Subramanian A.K., Sun C.T. Continuum interpretation of virial stress in molecular simulations // International Journal of Solids and Structures. - 2008. - No. 45. - P. 4340-4346. DOI: 10.1016/j.ijsolstr.2008.03.016
- Calculation of stress in atomistic simulation / J.A. Zimmerman, E.B. Webb III, J.J. Hoyt, R.E. Jones, P.A. Klein, D.J. Bammann // Modelling and Simulation in Materials Science and Engineering. - 2004. - Vol. 12, iss. 4. - P. S319-S332. DOI: 10.1088/0965-0393/12/4/S03
- Liu B., Qiu X. How to compute the atomic stress objectively // Journal of Computational and Theoretical Nanoscience. -2008. - Vol. 6, no. 5. - P. 1081-1089. DOI: arXiv:0810.0803v2
- Yang J., Komvopoulos K. A stress analysis method for molecular dynamics systems. // International Journal of Solids and Structures. - 2020. - Vol. 193-194. - P. 98-105. DOI: 10.1016/j.ijsolstr.2020.02.003
- Gasemi A., Gao W. A method to apply Piola-Kirchhoff stress in molecular statics simulations // Computational Materials Science. - 2021. - Vol. 195. - P. 110496. DOI: 10.1016/j .commatsci.2021.110496
- Investigation of crack tip dislocation emission in aluminum using multiscale molecular dynamics simulation and continuum modelling / V.I. Yamakov, D.H. Warner, R.J. Zamora, E. Saether, W.A. Curtin, E.N. Glassgen // Journal of the Mechanics and Physics of Solids. - 2014. - Vol. 65. - P. 35-53. DOI: 10/1016/j.jmps.2013.12.009
- Nikravesh Y., Sameti A.R., Jkkoei A.R. An atomistic-continuum multiscale analysis for heterogeneous nanomaterials and its application in nanoporous gold foam // Applied Mathematical Modelling. - 2022. DOI: 10/1016/j.apm.2022.02.029
- Ganesh K.V., Patra P.K., Travis K.P. Multiscale modelling of impact through molecular dynamics and smooth particle hydrodynamics // Physica A. - 2022. - Vol. 593. - P. 126903. DOI: 10/1016/j .physa.2022.126903
- A predictive discrete-continuum multiscale model of plasticity with quantified uncertainty / J. Tan, U. Villa, N. Shamsaei, S. Shao, H.M. Zbib, D. Faghihi // International Journal of Plasticity. - 2021. - Vol. 138. - P. 102935. DOI: 10/1016/j.ijplas.2021.102935
- Multiscale Concurrent Atomistic (CAC) modeling of multicomponent alloys / K. Chu, A. Diaz, Y. Chen, T. Zhu, D.L. McDowell // Computational Materials Science. - 2022. -Vol. 201. - P. 110873. DOI: 10/1016/j.commatsci.2021.110873
- Hello G., Tahar M.B., Roeland J.-M. Analytical determination of coefficients in crack-tip stress expansions for a finite crack in an infinite plane medium // International Journal of Solids and Structures. - 2012. - Vol. 49. - P. 556-566. DOI: 10.1016/j.ijsolstr.2011.10.024
- Nejati M., Ghouli S., Ayatollahi M.R. Crack tip asymptotic fields in anisotropic planes: Importance of higher order terms // Applied Mathematical Modelling. - 2021. - Vol. 91. - P. 837862. DOI: 10.1016/j.apm.2020.09.025
- Elastic stress analysis of blunt V-notches under mixed mode loading by considering higher order terms / A.M. Mirzaei, M.R. Ayatolahi, B. Bahrami, F. Berto // Applied Mathematical Modelling. - 2020. - Vol. 78. - P. 665-684. DOI: 10.1016/j.apm.2019.09.049
- Vivekanandan A., Ramesh K. Study of interaction effects of asymmetric cracks under biaxial loading using digital pho-toelasticity // Theoretical and Applied Fracture Mechanics. -2019. - Vol. 99. - P. 104-117. DOI: 10.1016/j.tafmec.2018.11.011
- Степанова Л.В. Экспериментальное и конечно-элементное определение коэффициентов многопараметрического асимптотического разложения М. Уильямса у вершины трещины в линейно-упругом изотропном материале. Часть I // Вестник Пермского национального исследовательского политехнического университета. Механика. - 2020. - № 4. -С. 237-249. DOI: 10.15593/perm.mech/2020.4.20
- Степанова Л.В. Экспериментальное и конечно-элементное определение коэффициентов многопараметрического асимптотического разложения М. Уильямса у вершины трещины в линейно-упругом изотропном материале. Часть II // Вестник Пермского национального исследовательского политехнического университета. Механика. - 2021. - № 1. -С. 72-85. DOI: 10.15593/perm.mech/2021.1.08
- Li Y., Zheng K. Crack tip asymptotic field coefficients analyses based on the extended finite element method using over-deterministic displacement field fitting method // Theoretical and Applied Fracture Mechanics. - 2021. - Vol. 113. - P. 102971. DOI: 10.1016/j.tafmec.2021.102971
- Ayatollahi M.R., Nejati M., Ghouli S. The finite element over-deterministic method to calculate the coefficients of the crack tip asymptotic fields in anisotropic planes // Engineering Fracture Mechanics. - 2020. - Vol. 231. - P. 106982. DOI: 10.1016/j .engfracmech.2020.106982
- Determination of SIFs and T-stress using an over-deterministic method based on stress fields: Static and dynamic / C. Hou, Z. Wnag, X. Jim, X. Ji, X. Fan // Engineering Fracture Mechanics. - 2021. - Vol. 242. - P. 107455. DOI: 10.1016/j .engfracmech.2020.107455.
- Patil P., Vyasarayani C.P, Ramji M. Linear least squares approach for evaluating crack tip fracture parameters using iso-chromatic and isoclinic data from digital photoelasticity // Optics and Lasers in Engineering. - 2017. - Vol. 93. - P. 182-194. DOI: 10.1016/j.optlaseng.2017.02.003
- Constantinescu A., Korsunsky A. Elasticity with Mathematica. An Introduction to continuum mechanics. - Cambridge: Cambridge University Press, 2007. - 267 p.
- Nordmann J., ABmus M., Altenbach H. Visualising elastic anisotropy: theoretical background and computational implementation // Continuum Mechanics and Thermodynamics. - 2018. -Vol. 30, no. 4. - P. 689-708. DOI: 10.1007/s00161-018-0635-9
- Gaillac R., Pullumbi P., Coudert F.-X. ELATE: an open -source online application for analysis and visualization of elastic tensors // J. Phys. Condensed Matter. - 2016. - Vol. 28, no. 27. -P. 275201. DOI: 10.1088/0953-8984/28/27/275201
- Daw M.S., Baskes M.I. Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals // Phys. Rev. - 1984. - Vol. B29 (12). - P. 6443.
- The improvement of mechanical properties of conventional concretes using carbon nanoparticles using molecular dynamics simulations / L. Zhao, M.K.M. Nasuton, M. Hekmatifar, R. Sabetvand, P. Kamenkov, D. Toghraie, A. Alizadeh, T. Ghahari // Scientific Reports. - 2021. - Vol. 11. - P. 20265. DOI: 10.1038/s41598-021-99616-y
- Stukowski A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool // Model. Simul. Mater. Sci. Eng. - 2010. - Vol. 18. - P. 015012.
- Sanford R.J., Dally J.W. A general method for determining mixed mode stress intensity factors // Engineering Fracture Mechanics. - 1972. - Vol. 4. - P. 357-366.
- Ramesh K., Gupta S., Kelkar A.A. Evaluation of stress filed parameters in fracture mechanics by photoelasticity- Revisited // Engineering Fracture Mechanics. - 1997. - Vol. 56, no. 3. -P. 25-45.
- Stepanova L.V., Belova O.N. A molecular dynamics simulation analysis of mixed mode crack growth // AIP Conference Proceedings. - 2021. - Vol. 2371. - P. 020012. DOI: 10.1063/5.0059574.
- Nirwal S., Katukam R. An approach for Coupling FEM&Molecular Dynamics // International Journal of Emerging Trends in Engineering Research. - 2015. - Vol. 3, no. 10. - P. 7-19.
- Chakraborty S., Ghost S. A concurrent atomistic-crystal plasticity multiscale model for crack propagation in crystalline metallic materials // Computer methods in Applied Mechanics and Engineering. - 2021. - Vol. 379. - P. 113748. DOI: 10.1016/j.cma.2021.113748
- Yasbolaghi R., Khoei A.R. A continuum-atomistic multi-scale analysis of temperature field problems and its application in phononic nano-structures // Finite Elements in Analysis & Design. - 2022. - Vol. 198. - P. 103643. DOI: 10/1016/j.finel.2021.103643


