Идентификация линейной искажающей системы с использованием ранговой обработки сигналов

I m l<—2~ где h, x, v - соответственно ИХ искажающей линейной системы с постоянными параметрами, полезный (входной) сигнал и помеха;

N - ширина “размаха" ИХ (не умаляя общности, положим, что N нечетно).

Будем считать, что последовательность h(m) не только ограничена по аргументу, но и неотрицательна. Предположим, кроме того, что влияние помехи мало по сравнению с динамическими искажениями, обусловленными линейной системой. Данная модель хорошо описывает такие процессы искажения сигналов (изображений), как, например, дефокусировка, смаз, влияние турбулентности среды распространения светового "потока и т.п. Наконец, будем считать, что входной сигнал х(п) является кусочно-постоянным. Примерами таких сигналов в определенной степени могут служить многие телевизионные изображения, результаты аэрофотосъемок и т.п.

Алгоритм ранговой обработки

Для получения оценки входного сигнала, используемого в процедуре идентификации, предлагается простой ранговый алгоритм - обобщенный экстремальный фильтр Его действие заключается в следующем. Искаженный сигнал обрабатывается М-точеч-ным скользящим "окном11. Из отсчетов, попавших в окно, строится вариационный ряд Текущий отсчет (центральный в окне) заменяется i-м или (M-i+D-м членом вариационного ряда в зависимости от того, который из них ближе по значению к текущему отсчету. Таким образом, результат ранговой обработки наблюдаемого сигнала (1) имеет вид:

х (п)

p(i)z если Ip(i)-y(n)|<|p(M-i+1)-у(п)I;

(?)

рСИ-i+D в противном случае, где p(i)z 1=1ZM - вариационный ряд, построенный по отсчетам y(n+k), k = ——^—,—^-

(предполагается, что М нечетное).

Разумеется, точно восстановить входной сигнал с помощью экстремального фильтра в реальных ситуациях невозможно. Так, в случае протяженной ИХ или большого размера окна обработки рангового алгоритма необратимо теряются короткие "ступеньки" кусочно-постоянного сигнала. В то же время границы между длинными интервалами постоянных знамений при наложенных ограничениях на ИХ могут восстановиться полностью, что в конечном счете и обеспечивает возможность решения задачи идентификации.

Алгоритм идентификации

При известной оценке входного сигнала х и выходном сигнале у может быть при менен любой из известных алгоритмов идентификации линейной системы [2]. Здесь мы воспользуемся простейшей процедурой решения уравнения (1) методом наименьших

А квадратов, то есть найдем оценку ИХ h(m) из условия минимума критерия

п =

M*N

Е h(m)x(n-m)-у(п)

где К - размер

обрабатываемого отрезка наблюдаемого сигнала у(п), п=1ZK (должно быть K>M+N-1).

Решение задачи оптимизации (3) приводит к системе линейных уравнений относительно h(ш):

^+1

M^N +1

5Z h(m)

хСп-ю)8(n-k)

n=^

M + N

y(n)x(n-k)z [kls^ti.

которая решается обычным способом.

Результаты экспериментов

Описанная процедура "слепой" идентификации исследовалась для одномерных и двумерных сигналов. В одномерном случае в качестве входного брался отрезок в 200 отсчетов дискретизированного обобщенного телеграфного сигнала со средней длиной "ступенек11, равной 7, и нормальным распределением постоянных значений на интервалах. Сигнал искажался системой с квазигауссовской ИХ при N=9 и дискретным "белым" нормальным шумом. Результаты идентификации ИХ для различных соотношений сигнал-шум по мощности D показаны на рис. 1, где для каждого D приведена соответствующая среднеквадратичная ошибка оценивания ИХ, вычисляемая по формуле :

Е^а ■ 4         .  [h(m)-h(rn)]^a.

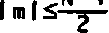
В двумерном случае в качестве входного сигнала использовалось "мозаичное" поле [3^ размером 32x32 с шириной полосы деления 7, которое искажалось аналогично одномерному случаю системой с "размахом" ИХ 5^Х5 . Результаты восстановления ИХ с соответствующими D и е показаны на рис. 2. Как в одномерном случае, так и в двумерном использовалась процедура ранговой обработки (2) при i=1. Рисунки демонстрируют хорошие результаты идентификации даже для довольно значительного шума .

Развитие метода

Использованный алгоритм идентификации является простейшим, с его помощью лишь демонстрируется работоспособность предлагаемого метода. Существуют довольно прозрачные способы повышения точности оценивания ИХ. Например, для снижения

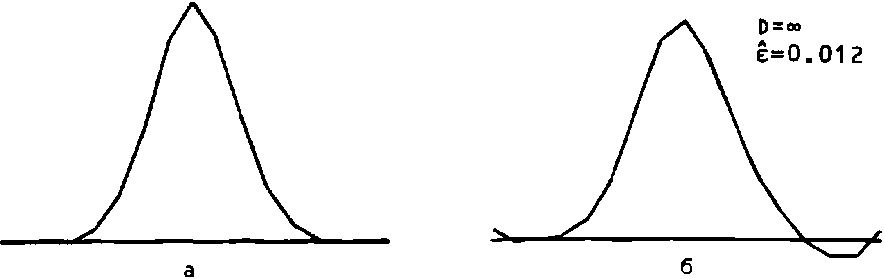
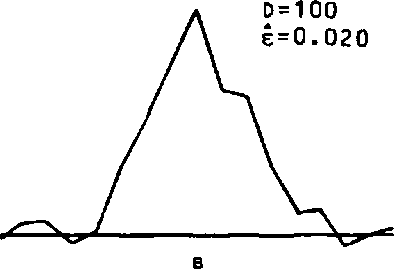
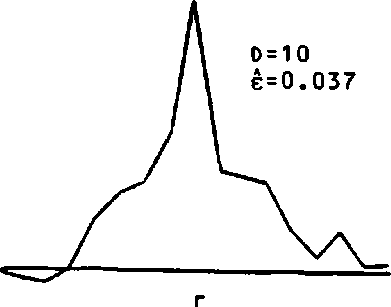
Рис. 1. Истинная (а) и идентифицированные (б, в, г) одномерные ИХ

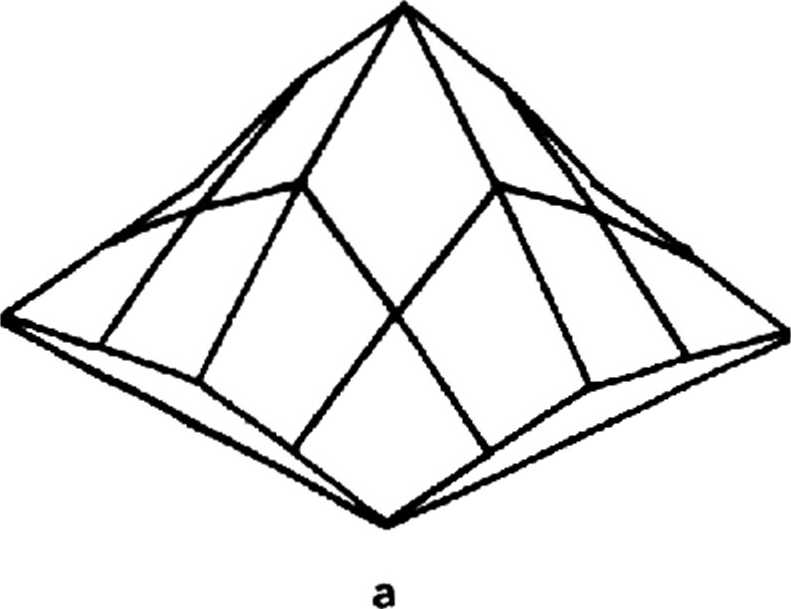
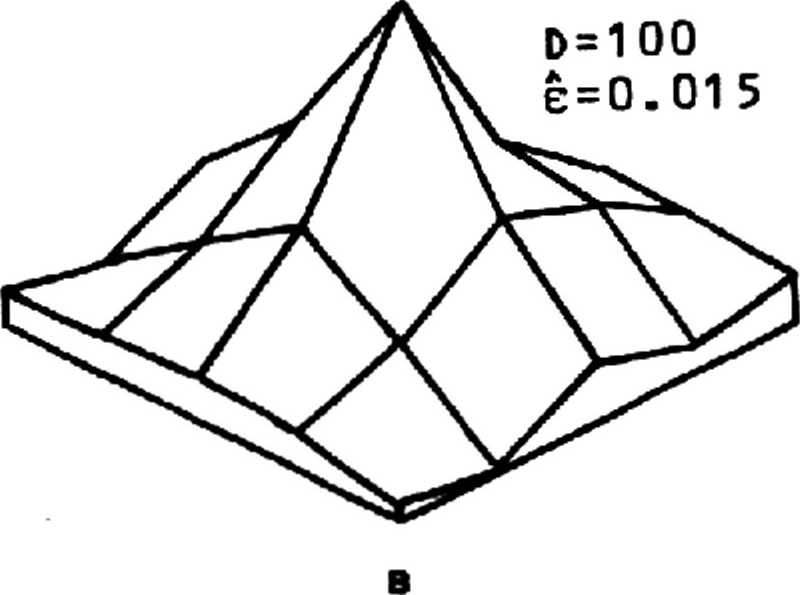
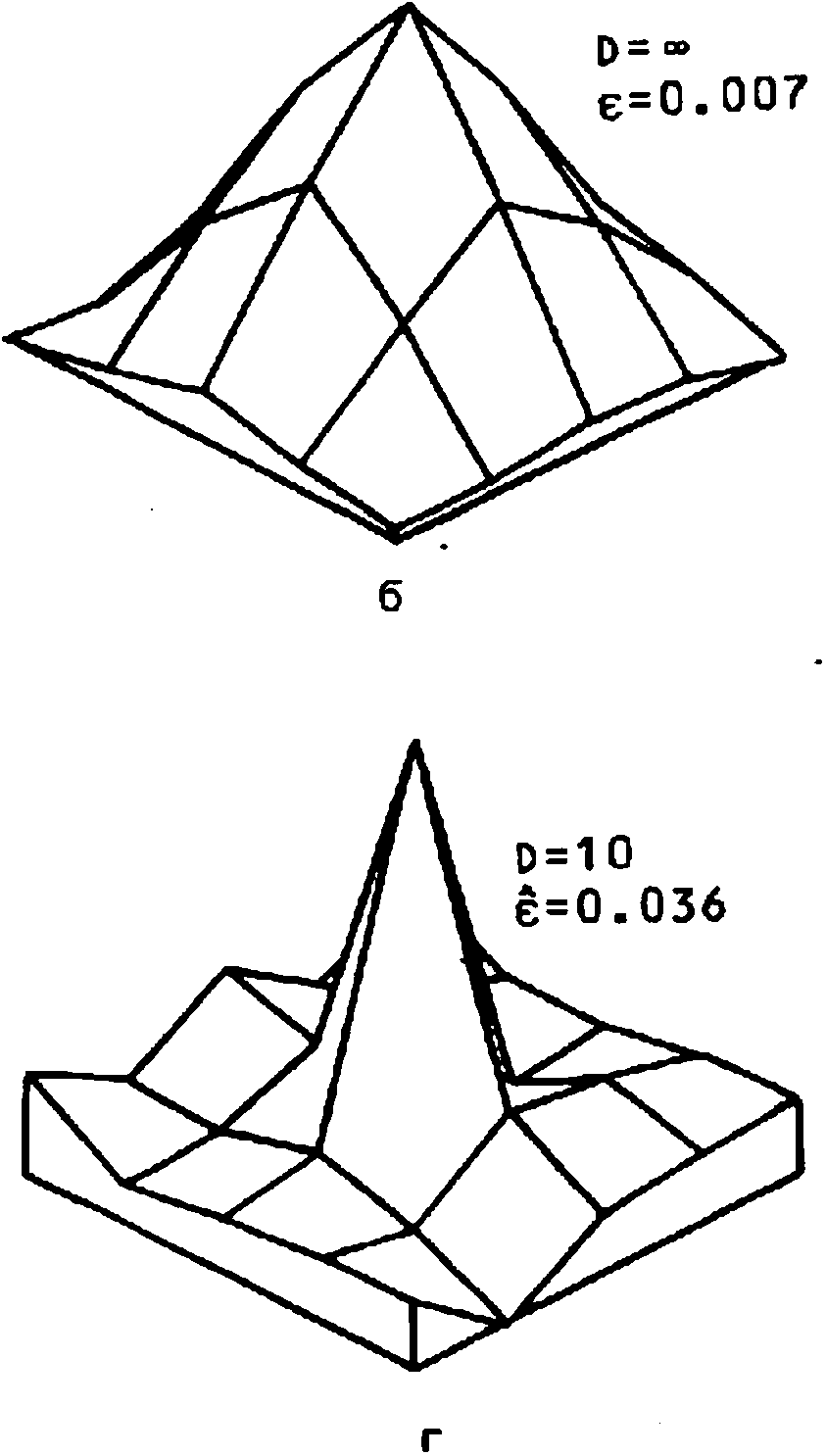
Рис. 2. Истинная (а) и идентифицированные (б, в, г) двумерные ИХ

влияния шумов можно предварительно сгладить выходной сигнал медианным фильтром. На рис. 3 представлены результаты идентификации без применения (а) и с применением (б) медианной фильтрации (точнее, использовался медианный фильтр каскадного типа [4]). При наличии импульсных шумов очевидна полезность применения обобщенного экстремального фильтра (2) с п>1. На рис. 4 приведены решения для i=1 (а) и i=2 (б). Повышению точности будет способствовать наличие априорных сведений о симметрии ИХ, а также использование алгоритмов идентификации, явным образом учитывающих ее неотрицательность. Решение, учитывающее симметричность ИХ, изображена на рис. 5 (сравнить с рис. 16).

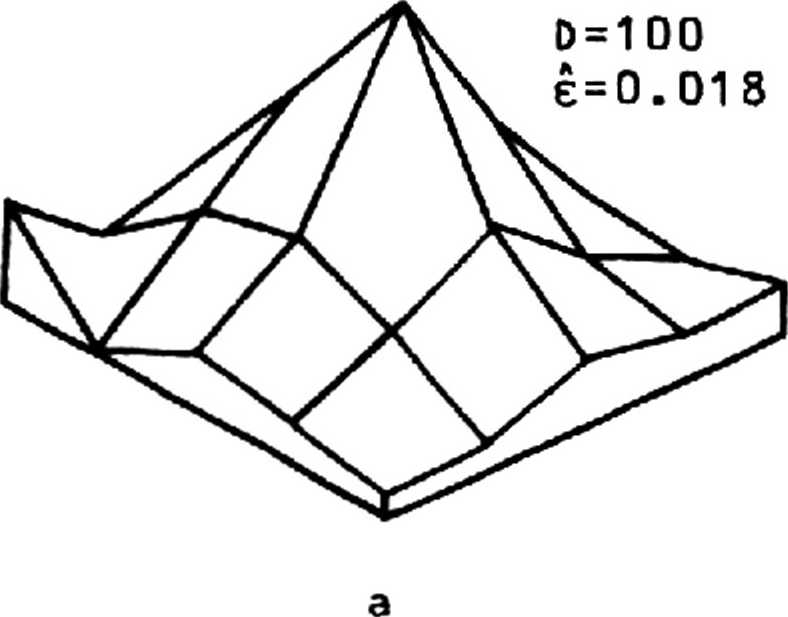
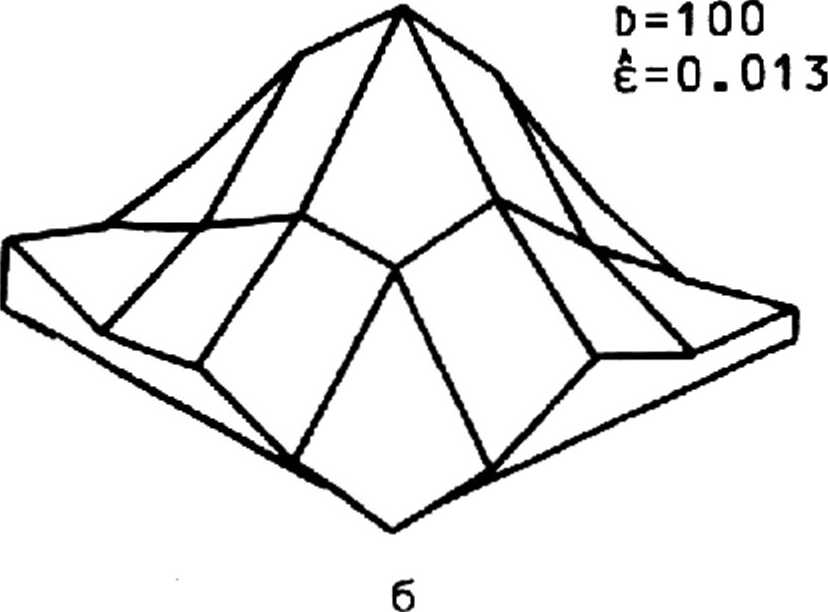
Рис. 3. Результаты идентификации двумерной ИХ без использования (а) и с использованием (б) медианной фильтрации

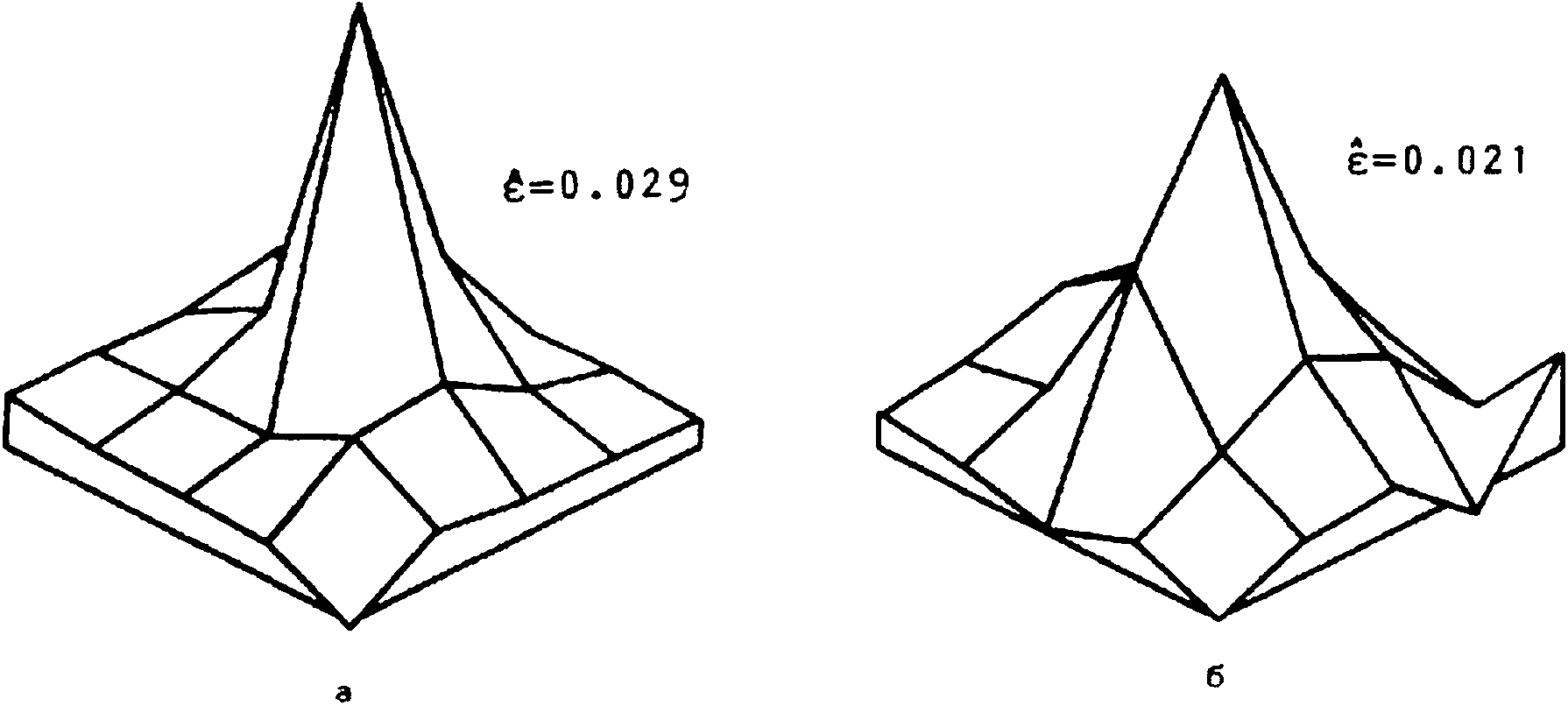
Рис. к. Результаты идентификации двумерной ИХ с помощью экстремального фильтра (2) для i=1 (а) и 1=2 (б) в случае импульсного шума

Результаты идентификации существенно зависят от выбора размеров окна обработки экстремального фильтра. Из очевидных соображений следует, что они должны быть близки к размерам "ступенек" исходного сигнала и к размерам ИХ системы. Кроме того, ясно, что повышение шумовой компоненты сигнала требует некоторого увеличения размеров окна, что усиливает сглаживание сигнала экстремальным фильтром. Экспериментальные результаты подтверждают описанные выше соображения (см. рис. 6, на котором изображены графики зависимости среднеквадратичной ошибки от размеров окна обработки для одномерного случая). Необходимо отметить, что все приведенные в статье решения соответствуют оптимальным размерам окна.

Результаты исследования предложенного здесь метода позволяют сделать вывод о целесообразности его использования для идентификации на кусочно-постоянных сигналах неотрицательной пространственно ограниченной ИХ линейной искажающей системы .

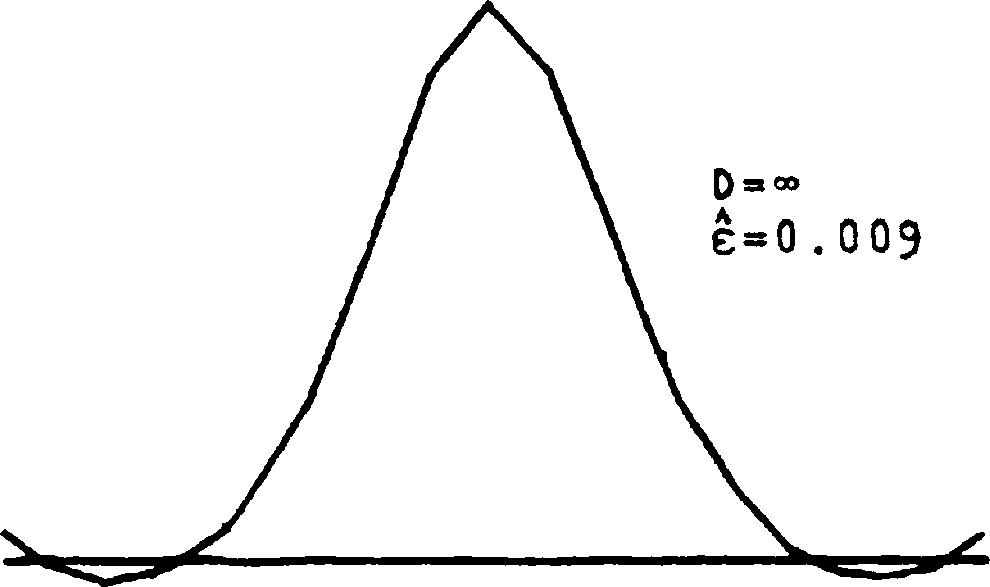
Рис. 5. Результат идентификации одномерной ИХ с учетом ее симметрии

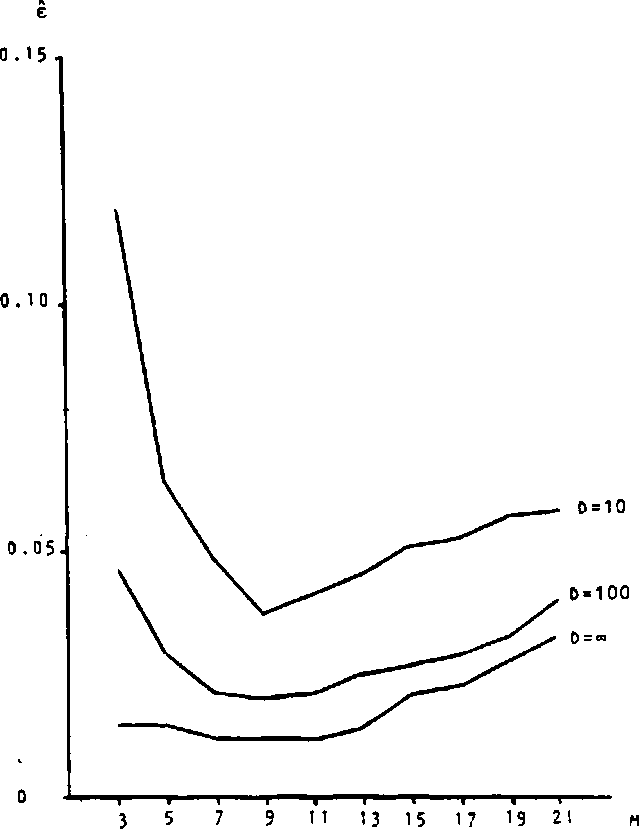
Рис. 6. Графики зависимости среднеквадратичной ошибки оценивания ИХ от размера окна обработки экстремального фильтра