Идентификация математической модели нагрева слябов в регулярном режиме

В работах [1–3] приведены алгоритмы, которые могут быть использованы для косвенного контроля температурных полей слябов в период выдержки при постоянной температуре печи. Алгоритмы позволяют, в частности, определять среднемассовую температуру заготовок и наибольший перепад температуры по их сечению, которые являются широко используемыми наряду с температурой поверхности, показателями качества нагрева массивных тел. Очевидно, что включение этих алгоритмов в состав алгоритмического

обеспечения АСУ ТП является значимым расширением вектора обратной связи по температурному состоянию объекта управления.

Вполне понятно, что контроль качества нагрева необходимо производить на выходе из печи, т. е. в ее последней – томильной зоне. При этом, решая задачу контроля, выгодно учесть, что в томильных зонах печей обычно имеет место регулярный режим нагрева [4–6] – в этом случае упомянутые алгоритмы контроля существенно упрощаются, что достаточно привлекательно для АСУ ТП, работающих в режиме реального времени.

Постановка задачи

Из-за сложности теплофизических явлений в печах практическое использование как алгоритмов контроля, так и непосредственно самих математических моделей предполагает их предварительную настройку на реальный процесс. Поэтому рассмотрим один из возможных методов настройки, основанный именно на закономерностях регулярного теплового режима. При этом следует иметь в виду, что решая задачу настройки алгоритмов, мы, по существу, решаем и задачу параметрической идентификации математической модели, с помощью которой они были получены.

Как это хорошо известно [7–12], нагрев слябов в томильных зонах методических печей с монолитным подом в этих зонах или же симметричный нагрев в печах с шагающими балками можно представить с помощью математической модели следующей структуры:

dt(x,x)    д ( дПхлЦ n         r n./n

• CP^T д, d, P’ ^^ X 0;

t(x, 0) = t0(x), 0 < x < L;(2)

• дt^ = 0,т>0;(3)

дх

/dtdV   а'..ш Ш., ()!,(> 0.

Здесь c, p и X - соответственно теплоемкость единицы массы, плотность и коэффициент теплопроводности, зависящие в общем случае от температуры t(x,x); x - пространственная координата; т - время; L - расчетное сечение заготовки; t⁰(x) - заданная функция, описывающая температурное поле металла на входе в зону; a - эквивалентный коэффициент теплоотдачи; t_n (т) - температура рабочего пространства печи (температура в зоне).

Из решения данной системы уравнений при постоянной температуре печи Сп (т) = const следует, что в регулярном режиме температура поверхности заготовки должна изменяться в соответствии со следующим выражением:

t(L, т) = t_n + A _r cos щ L • exp (-ц ^ ат),                                                     (5)

где Лг - коэффициент, зависящий от температурного поля заготовки в начале периода выдержки; а = ^ - коэффициент температуропроводности; рг - первый корень уравнения ^ = ctg(^L).

Настроечная часть алгоритмов контроля, как это известно [1–3], выражается через параметр р_г поэтому задача настройки (параметрической идентификации) заключается в определении этого коэффициента по экспериментальным данным. Настройка и самой модели (1)–(4) также может быть сведена к определению по экспериментальным данным того же самого параметра p_r λμ так как a = —-¹- ctg( g ₁

, а коэффициент теплоотдачи α и является наиболее трудноопределяемым па-

раметром модели, должное определение которого и обеспечивает настройку собственно всей модели на реальный процесс.

Уравнение (5) совместно с результатами измерения на печи значений t(L, т) и tn используем в качестве исходной информации для идентификации параметра рг При этом под t(L,т) понимается температура поверхности металла, измеренная каким-либо способом, устраняющим влияние поверхностного слоя окалины [11]. Таким образом, за счет определения соответствующего значения рг (а следовательно, и коэффициента теплоотдачи a ) обеспечивается суммарный учет влияния на нагрев металла как условий теплообмена с печной атмосферой всей заготовки в целом, так и поверхностного слоя окалины. Кроме того, при решении задачи идентификации учтем, что в реальных условиях режим Сп = const поддерживается в печах системами автоматического регулирования все-таки приближенно, поэтому в последующих выкладках будем использовать реально измеренное значение температуры в зоне, т. е. будем считать, что tn = Сп(т).

Общее решение задачи

Следует отметить, что поскольку по условиям задачи уравнение (5) содержит два неизвестных (неизмеряемых) параметра Лг и р^ то для идентификации необходимо иметь результаты измерений не менее чем в два различных момента времени. При этом если определять параметр рг по результатам измерений в моменты времени т1 и т2 после наступления регулярного режима, то получим следующую формулу для нахождения этого параметра:

Pi =

I

i

а(т₂-Т 1 )

I  / £пСч2-£(М12\

■     kt n (T₂)-t(L,T₂)Z

Понятно, что это наиболее простой и наименее точный метод определения параметра рг

При наличии измерительной информации о нужных температурах в более чем в двух точках задачу следует решать по методу наименьших квадратов, минимизируя величину

](Ai, pi) = S”=i{ln[tn(Tf) - t(L,Tt)] - in(-^i) - In(cospiL) + i^aq}2,                    (7)

полученную путем записи уравнения (1) в логарифмическом масштабе с целью получения решения в явном виде относительно g_i и суммирования по точкам квадратов невязок между расчетными и экспериментальными данными. Здесь, приравнивая частные производные d](A_i, p_i)/dA_i, d](A_i, p_i)/dp_i к нулю и решая полученную систему уравнений относительно неизвестных A_i и р₁, получим следующую формулу для вычисления параметра р:

/Ё^ТтПпё^^-^момТпя^^

J                 "ЛмУ'^! рд'-аУ" р;'                 '

Аналогично при наличии измерительной информации о температуре поверхности металла на некотором отрезке времени [тн, тк], где тк > тн, параметр р1 определяем из решения следующей задачи оптимизации:

min^,g1 ^{In^^i) - t(L, т;)] - ln(-Ai) - ln(cosp1L) + ^ау}2 dT.

В этом случае

P i

Х'кт 1п[Сп(т)—С0Ъ,т)]Йт—1/2-(тн+тк)-£Гк ln[tn(T)—t(L,T)]dr τн                                           τн аЛ-рн +тку (тк -тн)-а/3 - (у -тн )            '

Апробация алгоритмов идентификации

Апробация алгоритмов (6), (8), (10) проводилась с использованием как реальных экспери- ментальных данных, так и данных, полученных с помощью вычислительного эксперимента на ЭВМ [12–15].

В результате вычислительного эксперимента было установлено, что из-за погрешности уста- новления регулярного теплового режима при конечных значениях времени выдержки алгоритмы

(6), (8), (10) дают некоторую ошибку в определении параметра рг Причем эта ошибка уменьшает- ся при использовании для идентификации более удаленных моментов времени. Так, например, когда a = — = 0,02 м2/ч; L = 0,1 м; X = 29 Вт/(м • °C); a = 435 Вт/(м2 • °C); Сп = 1200 °C, а тем- выражением 1100 - 100 (1 - ^), °C,

пературное поле в начале периода выдержки описывается точное значение параметра р равно 9,88 м i. Используя формулу (6) для данных о температуре поверхности при г1 = 9 мин и т2 = 12 мин, получим, что р = 9,50 м i, если же будем использовать данные при г1 = 11 мин, т2 = 14 мин, то получим, что pi = 9,83 м-1. Как видно, погреш ность определения р заметно уменьшилась.

Примечание. Данные о численных значениях температуры поверхности в период выдержки и точное значение ^₁ брали из точного выражения температурного поля заготовки для этого периода, приведенного, например, в работе [16].

Кроме того, как и следовало ожидать, алгоритм (6) является более чувствительным к случайным погрешностям данных о температуре поверхности, чем алгоритмы (8) и (10), вследствие использования результатов измерения только в двух точках. Алгоритмы же (8), (10) являются практически равноценными.

На рисунке приведена кривая температуры поверхности заготовки, вычисленная по настроенному по алгоритму (8) уравнению (5). Крестиками указаны используемые при этом экспериментальные точки. Другие данные для этого случая таковы: L = 0,0625 м, a = — = 0,02 м2/ч; X =29 Вт/(м ■ °C).

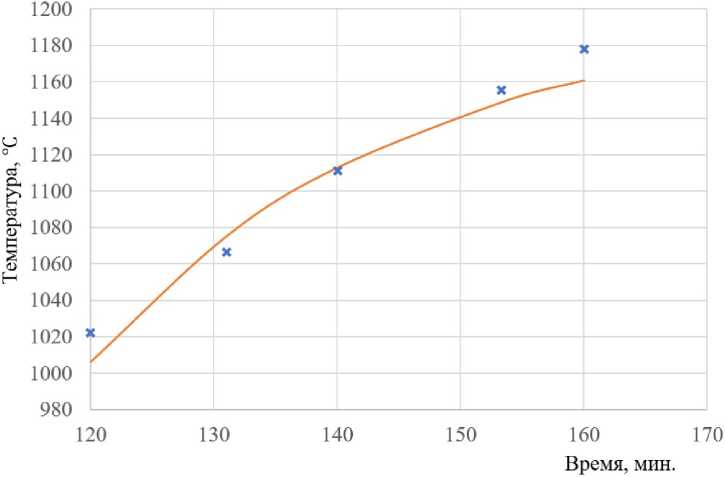
Расчетная (сплошная кривая) и экспериментальная (крестики) температуры поверхности металла в томильной зоне печи Calculated (solid curve) and experimental (crosses) metal surface temperatures in the soaking zone of the furnace

Как видно из рисунка, близость расчетных и экспериментальных данных достаточно удовлетворительная. Здесь также было установлено, что р1 = 10,94 м-1, поэтому реальное значение эквивалентного коэффициента теплоотдачи для томильной зоны будет таким а = 258,81 Вт/(м2 • °C), что вполне соответствует практическим данным. Также к месту заметим, что попутно можно определить и коэффициент Лъ и начальное температурное поле для этапа выдержки. Так, в данном случае оно будет описываться следующим (конечно, приближенным) соотношением: 1200 — 250,05 • cos(10,94 • %), C. Все это подтверждает решаемость задачи о наблюдаемости температурного поля металла при нагреве в печах [17].

Оценка влияния погрешностей измерения

При моделировании исследовали также влияние погрешности результатов измерения температуры поверхности на точность оценки коэффициента теплоотдачи а, параметра р1 и наибольшего перепада по сечению сляба. Для этого на значение температуры поверхности, полученное из точного выражения температурного поля [16], накладывалась постоянная систематическая погрешность положительного или отрицательного знака. С практической точки зрения наибольший интерес представляет определение влияния положительной систематической погрешности, поскольку при нагреве поверхность заготовки, как правило, покрыта слоем окалины, имеющим более высокую температуру, чем неокисленный металл. Исследование проводили для алгоритма (8), рассматривая период выдержки для вышеприведенных условий вычислительного эксперимента на отрезке времени [9; 16] мин. Результаты этих исследований приведены в таблице. Здесь

1-cos^L cos g ₁L

к =

– коэффициент преобразования измеряемой при контроле разности температур ра- бочего пространства томильной зоны и поверхности металла в ней в перепад температуры по сечению заготовки At = t(L,т) — t(0,т) : At = к • ^п(т) — t(L,т)].

Как видно из таблицы, погрешность оценки коэффициента теплоотдачи α может быть доста- точно существенной. Объясняется это высокой чувствительностью данного параметра к погреш- ности определения коэффициента р1, в данном случае при р1 = 9,88 м 1 получается, что

X -ctg( g ₁L)+ X - g ₁L/sin²( g ₁L) ctg² C n ^ L)

д а

3^

= 138,58 Вт/(м • °C), поэтому будет Аа = 138,58 • Ар1, что несложно проследить по числовым данным таблицы. Здесь Аа и Ар1 - погрешности определения параметров. Однако в данном случае важно прежде всего влияние этого параметра на точность расчета по модели температурного поля слябов. А здесь, как это следует из приведенных данных, можно допускать и заметную погрешность определения α, что в значительной мере обуславливается особенностями режима томления. К месту также заметим, что в данном случае при р1 = 9,88 м-1 дк LsinO L)

получается, что — =       = 0,2754 м, а это указывает на вполне приемлемую для практики чувствительность коэффициента к к погрешности Apr

Влияние систематической погрешности на точность оценки идентифицируемых параметров и перепада температуры The influence of systematic error on the accuracy of the assessment of the identified parameters and temperature difference

№ п/п	Погрешность измерения температуры поверхности, °C	Цг м 1	Оценка к, отн. ед.	Погрешность оценки перепада температуры по сечению заготовки, °C	Оценка коэффициента теплоотдачи, Вт/(м2 • °C)
1	0	9,81	0,80	2	425
2	5	10,16	0,90	3	475
3	10	10,56	1,03	7	541
4	15	10,99	1,21	13	624
5	20	11,53	1,47	22	753
6	25	12,11	1,85	37	933

Из приведенных данных также видно, что если считать точность определения температурного поля заготовки (в том числе и перепада) в 25 °C приемлемой [18], то погрешность определения температуры поверхности металла для идентификации параметра р1 и контроля перепада температуры по сечению должна быть порядка 21 °C. С увеличением погрешности измерения температуры поверхности ошибка в определении перепада температуры начинает существенно возрастать. Погрешности в оценке At при отрицательной систематической погрешности измерения температуры поверхности неокисленного металла получаются меньше: так, при погрешности в -25 °C максимальный модуль ошибки в определении перепада температуры составляет всего 13 °C.

В процессе моделирования было установлено, что погрешность оценки перепада температуры по сечению монотонно убывает при увеличении времени выдержки. Так, для случая строки 6 таблицы модуль погрешности оценки перепада при т = 9 мин составляет 37 °C , а при т =16 мин уже только 21 °C. Объясняется это тем, что взаимосвязь между погрешностью оценки перепада температуры SAt , погрешностью оценки коэффициента преобразования Sk и погрешностью измерения температуры поверхности St(L, т) может быть приближенно представлена следующей формулой:

SAt = 5к • [tn(т) - t(L, т)] - k5t(А,т) - 5к • 8t(L,т). (11)

Как это нетрудно видеть из (11): поскольку с увеличением времени выдержки величина [t п (т) - t(L,т)] уменьшается, то и погрешность оценки перепада будет снижаться. Заметим, что при выводе формулы (11) считалось, что погрешности в измерении и стабилизации температуры рабочего пространства зоны нет.

Если же для идентификации параметра р1 использовать точные данные о температуре поверхности, а при последующем контроле перепада допускать возможность ее измерения с погрешностью, то, как это следует из (11), при определении допустимой погрешности измерения температуры поверхности следует исходить из зависимости

|SAt| = k|St(L, т)|. (12)

Так, для вышеприведенных условий при допустимой погрешности оценки перепада в 25 °C погрешность измерения температуры поверхности не должна превышать 31 C. Если же, следуя [18], считать, что погрешность оценки всего температурного поля сляба, в том числе и погрешность измерения его температуры поверхности, не должна превышать 25 C, то при такой погрешности измерения температуры поверхности ошибка в оценке перепада будет равна 20 °C.

Идентификация при несимметричном теплообмене

Рассмотрим теперь особенности настройки модели для случая, когда несимметрия заключается лишь в неравенстве коэффициентов теплоотдачи на металл с разных сторон обогрева, а температуры рабочего пространства в верхних и нижних зонах одинаковы. При этом отметим, что, хотя в нижних зонах печей для компенсации несимметрии нагрева обычно и поддерживается более высокая температура, чем в верхних зонах, тем не менее нет никаких не только принципиальных, но и просто практических трудностей для реализации такого режима. Объясняется это тем, что величина превышения температуры, как правило, невелика, где-то порядка 40 — 100 град., и устранение ее не приводит к каким-либо серьезным потерям в качестве нагрева. Во всяком случае, на осуществление такого режима выдержки всегда можно согласиться ради предлагаемого достаточно привлекательного решения задачи идентификации модели.

Суть способа настройки модели в данном случае заключается в следующем. В процессе текущей выдержки посредством инструментального контроля определяются реальные зависимости t(0, т) и t(L, т) в отдельные моменты или на определенном отрезке времени. При этом в соответствии с теорией регулярного теплового режима считается, что эти зависимости описываются следующими уравнениями:

t(0, т) = t n + Л ? • exp (—в ? т);          (13)

t(L, т) = t_n + Л ? • exp (—в ? т).          (14)

Далее, используя точечный или интегральный метод наименьших квадратов, следует определить численные значения коэф-

фициентов Л⁰, Л ? , в_г После этого, зная структуру зависимостей этих коэффициентов

от неизвестных параметров системы «печь – нагреваемый металл» (для этого можно использовать решение рассматриваемой задачи несимметричного нагрева, приведенное, например, в [19]), составляют три уравнения,

решая которые, находят реальные численные значения параметров настройки. Отметим, что

в данном случае из трех неизвестных параметров системы «печь – нагреваемый металл» настроечными являются лишь два, именно они характеризуют внешний теплообмен ме-

талла и через них можно определить реальные численные значения коэффициентов теплоотдачи, третий же неизвестный коэффициент не представляет для нас прямого интереса. Поэтому приведем формулы для вычисления лишь настроечных коэффициентов – коэффициентов теплоотдачи для верхней a_L и нижней а₀ поверхностей сляба:

_а = 2 Z ^ o - ⁽ tg o — Y ) .

^L     L   1+ y -tg a ^;

_a = 2. ^ O '(t ^g o + ^Y )

⁰     L   1— y -tg a ’

где a = 2 jeja; y =

л ^ —л ?

^+^ctga, а расчетная

толщина L равна всей фактической толщине сляба.

Выводы

Рассмотрено решение задачи параметрической идентификации модели нагрева металла в томильных зонах методических печей в условиях регулярного теплового режима. Результаты работы могут быть использованы при создании и совершенствовании алгоритмического обеспечения АСУ ТП нагревательных печей.