Идентификация математической модели теплового состояния гидросистемы летательного аппарата
Автор: Николаев В. Н.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Авиационная и ракетно-космическая техника
Статья в выпуске: 1 т.24, 2023 года.
Бесплатный доступ
Предложен метод математического моделирования теплового состояния гидросистемы летательного аппарата. Математическая модель представляет собой систему дифференциальных уравнений в частных производных для углепластиковой композитной теплоизоляции и обыкновенных дифференциальных уравнений для элементов гидросистемы, описывающих их теплообмен с воздушной средой и окружающими поверхностями. Для решения прямой задачи теплового состояния элементов гидросистемы, т. е. для решения жесткой системы обыкновенных дифференциальных уравнений, использовали численную схему типа Розенброка второго порядка аппроксимации для неавтономных систем и решение системы дифференциальных уравнений с частными производными метода Монте-Карло на основе вероятностного представления решения в виде математического ожидания функционала от диффузионного процесса. Обратная задача теплового состояния элементов гидросистемы решена композицией метода наискорейшего спуска, метода Ньютона и квазиньютоновского метода Бройдена - Флетчера - Гольдфарба - Шэнно. Разработана математическая модель теплового состояния агрегата гидросистемы в негерметическом отсеке летательного аппарата и оценены доверительные интервалы каждого из искомых коэффициентов модели с использованием распределения при доверительной вероятности b = 0,95.
Математическая модель, дифференциальные уравнения, гидросистема летательного аппарата, параметрическая идентификация, доверительные интервалы коэффициентов модели
Короткий адрес: https://sciup.org/148326246
IDR: 148326246 | УДК: 629.7.018. | DOI: 10.31772/2712-8970-2023-24-1-136-143
Текст научной статьи Идентификация математической модели теплового состояния гидросистемы летательного аппарата
При проведении проектирования и стендовых испытаний гидросистемы летательного аппарата используют математическое моделирование теплового состояния гидросистемы. Тепловое состояние гидросистемы определяется температурой воздушной среды, окружающих элементов гидросистемы поверхностей и др. Параметры теплообмена определяются теплофизическими параметрами агрегатов и трубопроводов гидросистемы, а также топологией их размещения в отсеке. Математическая модель строится по результатам лётного эксперимента при максимальных диапазонах параметров режима полёта и воздушной среды за бортом.
Математическая модель представляет собой систему дифференциальных уравнений в частных производных для углепластиковой композитной теплоизоляции и обыкновенных дифференциальных уравнений для элементов гидросистемы. При идентификации математической модели требуются эффективные методы решения дифференциальных уравнений в частных производных и обыкновенных дифференциальных уравнений, а также методы параметрической идентификации. Кроме того, необходимо оценить доверительные интервалы каждого из искомых коэффициентов модели.
Физическая модель теплового состояния элементов гидросистемы летательного аппарата
Тепловое состояние элементов гидросистемы летательного аппарата определяется теплообменом внешней поверхности корпусов агрегатов и трубопроводов с окружающими поверхностями и воздушной средой. Кроме того, тепловая энергия в элементах гидросистемы подводится и отводится гидрожидкостью и системой обеспечения теплового режима.
Корпусы агрегатов гидросистемы и трубопроводы летательного аппарата закрыты углепластиковой композитной теплоизоляцией.
Математическая модель теплового состояния элементов гидросистемы летательного аппарата
Математическая модель теплового состояния элементов гидросистемы состоит из дифференциальных уравнений, описывающих теплообмен углепластиковой композитной теплоизоляции и дифференциальных уравнений теплового баланса обшивки, воздушной среды в отсеке, исследуемого агрегата или трубопровода и эффективного оборудования [1–4]:
T cov , t =3 1 P V ( t ) V ar , out ( t ) [ T e ( t ) - T cov ( t )] -3 2 в 9 17 ( t ) [ T cov ( t ) - fr ( t )] -
-3 з *
T cov ( t )
T eq ( t )
>-9 4 *
T cov ( t )
T eq , ef ( t )
> +
+9 18 в 9 17( t )[ Te ( t ) - T cov ( t )] + 3 19
pV ( t ) d pV ( t )
T cv ( t ) d t
x [ T e ( t ) T cov ( t )] + 9 21 Q cov , out
T art = $ 5 в 9 17 ( t ) [ TC ov ( t ) - T al r ( t )] + $ 6 в( t ) [T_ ( t ) - T„ ( t )] +
+ $ 20 pV^ d^ V Tt) [ T cov ( t ) — T ar ( t )] — $ 7 в 9 17 ( t ) [ T ar ( t ) - T eq ( t )] - Tcov ( t ) d t
-M^C t )[ Tmr ( t ) — T eq , ef ( t )] + $ 22 . (2)
T eq , t = $ 9 в $ 17 ( t )[ T ar ( t ) - T eq ( t )] + $ 10 <
+$ 11 <
T eq , ef ( t )
T cov ( t ) 1 4
T eq ( t ) 1 4
M12 ( T q - T eq ).
T eq , ef , t = $ 13 в $ 17 ( t ) [Tmr ( t ) - T eq , ef ( t )] + $ 14 <
T cov ( t )
> +
T eq , ef ( t )
T eq T eq , ef ( t )
T eq , ef ( t )
’+ $ 16 .
где T lq – температура гидрожидкости, протекающей в агрегате или трубопроводе; T cov , T air , T eq , T eq , ef в выражениях (1)–(4) с индексом t означает дифференцирование по времени t температуры обшивки, воздушной среды в отсеке, поверхности теплоизоляции агрегата или трубопровода, эффективного оборудования, окружающего исследуемый агрегат или трубопровод соответственно; pV - плотность воздуха за бортом; 0 = [и 1 ,и 2 , „.,u 17 ] T - вектор коэффициентов модели; T – верхний индекс, обозначающий операцию транспонирования.
Вместо расчётных значений α eq коэффициента теплоотдачи конвекцией исследуемого агрегата или трубопровода введено произведение измеряемых плотности воздуха за бортом ρ V и числа Маха M полёта летательного аппарата при M < 1 и произведение р V M 2 при M > 1.
В общем виде процесс теплопередачи в углепластиковой теплоизоляции описывается уравнениями [5; 6]:
C cv ( x ) T cv , t = ( X cv ( x ) T cv , x ) x , 0 < x < l , 0 < t ^ t k ; (5)
|
X cv ( x ) F cv T cv , x = a cv , out ( t ) F cv ( T cv ( t , x ) - Tair ( t )) + Q cv , out , |
x = 0; |
(6) |
|
^ cv ( x ) F cv T cv,x = a C v,in ( t ) F cv ( TC v,„ ( t ) - T cv ( t , x )) + Q cv,in , |
x = l ; |
(7) |
T cv (0, x ) = T )( x ), 0 < x < l , (8)
В уравнениях (5)–(8) использованы следующие обозначения:
Tcv (t, x) – температура теплоизоляции; Tcv,in (t) – температура внутренней поверхности теп- лоизоляции; Tcv,t – первая производная Tcv по t ; Tcv,x – первая производная Tcv по x; Tcv,x,x – вторая производная Tcv по x; Ccv (x) – объемная теплоемкость теплоизоляции, определяемая теплоемкостью композита Сcompo и теплоемкостью воздуха Сair ; λcv (l) – теплопроводность теплоизоляции, определяемая теплопроводностью композита λcompo и теплопроводностью воздуха λair ; αcv,out – коэффициент теплоотдачи наружной поверхности агрегата или трубопровода; αcv,in – коэффициент теплоотдачи внутренней поверхности агрегата или трубопровода; Fcv – площадь агрегата или трубопровода при наружном и внутреннем теплообмене; Qcv,out – тепловая энергия внешних источников; Qcv,in – тепловая энергия внутренних источников; l – толщина теплоизоляции.
Решение прямой задачи теплового состояния элементов гидросистемы
Обыкновенные дифференциальные уравнения (1)–(4) составляют следующую систему уравнений:
Yt=F(Y(t,Θ)), t∈(0,tt); Yt=YΘ, Y∈Rs; Θ∈Rr,(9)
где Y = [ T cov , T air , T eq , T eq , ef ] T – вектор параметров теплового состояния гидросистемы; Y t – вектор первых производных Y по t .
Решение жёсткой системы (9) обыкновенных дифференциальных уравнений предлагается проводить методом Розенброка по следующей схеме [7]: **
Yn+1=Yn+αK1+(1-α)K2;(10)
——
K1 =h(I-αhFY(Yn,tn,Θ))-1F(Yn,tn+αh,Θ);(11)
K 2 = h (I-ahFY (Y„, tn, 0))-1 F (Y„, tn +aK1, t„ + 2a h, 0); a = 1 -1)41,(12)
где Y n , Y n +1 – решение системы, полученной на n -й и ( n + 1) -й итерациях, соответственно; F – правая часть системы; F Y – матрица Якоби; I – единичная матрица; h – шаг интегрирования.
Решение системы дифференциальных уравнений с частными производными (5)–(8) предлагается определять методом Монте-Карло со сглаженными коэффициентами в виде математического ожидания функционала от диффузионного процесса [8–10].
Расчёт траекторий диффузионного процесса в ячейках теплоизолятора осуществляется методом Эйлера как блуждание по движущимся сферам.
Алгоритм параметрической идентификации математической модели теплового состояния элементов гидросистемы
Определение вектора коэффициентов Θ модели теплового состояния элементов гидросистемы будем определять минимумом функции Φ ( Θ ) взвешенной суммы квадратов невязок [11] с помощью итерационного алгоритма минимизации:
N
Φ ( Θ ) = ∑ [ Y j - F ( Θ , U j )] T R - j 1 [ Y j - F ( Θ , U j )], (13)
j = 1
где N – число точек по времени; U j – вектор управления; R j – ковариационная матрица неопределённостей параметров теплообмена.
Параметрическую идентификацию математической модели теплового состояния элементов гидросистемы предлагается проводить композицией метода наискорейшего спуска, метода Ньютона и квазиньютоновского метода Бройдена – Флетчера – Гольдфарба – Шэнно [12].
Оценивание коэффициентов математической модели теплового состояния элементов гидросистемы
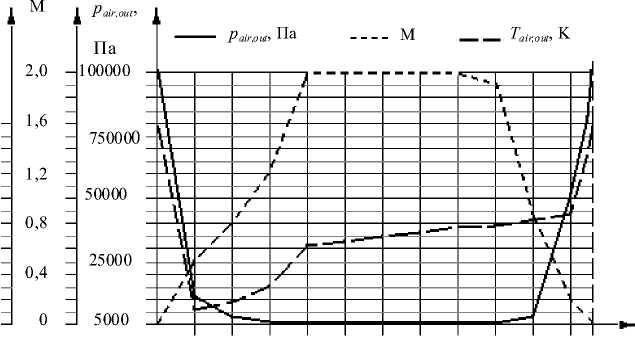
Предложенный теоретический метод был использован для построения математической модели теплового состояния гидросистемы в негерметическом отсеке летательного аппарата, ко- торая представляет собой систему агрегатов и трубопроводов в углепластиковой теплоизоляции. Параметры режима полёта и воздушной среды за бортом модели применения летательного аппарата приведены на рис. 1.
Критерием при оптимизации коэффициентов модели гидросистемы является температура гидрожидкости до 333 K. Температура воздуха в отсеке до 400 К.
Tair,out ,
K
0 3600 7200 10800 14400 18000 t , c
Рис. 1. Параметры режима полёта и воздушной среды за бортом модели применения летательного аппарата:
p air,out – давление воздуха за бортом за пределами теплового пограничного слоя;
M – число Маха на внешней границе пограничного слоя; T air,out – температура воздуха за бортом за пределами теплового пограничного слоя
Fig. 1. Parameters of the flight mode and the air environment overboard of the aircraft application model: p air,out – air pressure outside the thermal boundary layer; M – Mach number at the outer boundary of the boundary layer; T air,out – air temperature outside the thermal boundary layer
Коэффициент теплопроводности углепластиковой теплоизоляции равен X cv = 8^10-2 Вт/(м<К).
Толщина углепластиковой теплоизоляции l агрегата приняли за 2∙10–2 м.
Полученные оценки коэффициентов модели 0 агрегата имеют следующие значения:
0 = [1,2584-lG-4 4,1542-10-1 5,3417^10-2 1,2215^10-2 5,3456-10-3
2,0357∙10–3 9,2045∙10–3 1,1904∙10–1 3,9123∙10–2 3,5162∙10–1
2,6877∙10–3 2,0979∙10–2 3,2077∙10–4 2,0343∙10–4 1,6850∙10–1
1,3344∙10–4 5,1202∙10–1] T .
Cовместные доверительные интервалы искомых коэффициентов модели
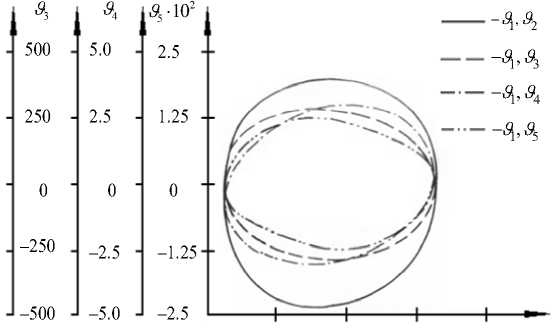
При большой размерности вектора коэффициентов модели 0 классическое использование совместной доверительной области [13] (рис. 2) связано со значительными проблемами.
В связи с этим было предложено использовать совместные доверительные интервалы А0 * коэффициентов в виде проекций совместной доверительной области на координатные оси пространства 0 . Это соответствует замене гиперэллиптической области на описанный вокруг неё гиперпараллелепипед. Было получено для A0 q следующее выражение [14; 15]:
A0 q ± XHif • q =1— r • (14)
F q AF q
-C -1 D C q D q ,
^ T s
F q =L e 1 - e q - 1 1 e q + 1 - e r J ; E q
Dq [ a q ... a ( q 4) q
a ( q + 1) q ••• arq J .
–25
–50
0 0.5 1.0 1.5 2.0 4
Рис. 2. Линии равного уровня функции невязки Ф ( 0 ) = 2734 вблизи действительных значений коэффициентов модели υ1,υ2,…,υ5
Fig. 2. Equal level lines of the residual function Ф ( 0 ) = 2734 near the actual values of the coefficients of the model υ1,υ2,…,υ5
a ll ”• 1( q - 1) a 1( q + 1) "• a l r
a ( q - 1)1 • • • a ( q - 1)( q - 1) a ( q - 1) ( q + 1) — a ( q - 1) r a ( q + 1)1 • a ( q + 1)( q - 1) a ( q + 1)( q + 1) • a ( q + 1) r
a r 1 • a r ( q - 1) a r ( q + 1) • a rr
* * *
где X 1-a — распределение; Fq - ( r x 1) - вектор; Eq , Dq - ( r - 1) x 1 - векторы;
Cq - (r -1) x (r -1) - матрица, которая получается из матрицы A вычеркиванием q -го столбца q -й строки.
При этом оценки доверительных интервалов А0 * полученных коэффициентов агрегата при доверительной вероятности β = 0,95 имеют следующие величины:
|
А0 * = |2,4339^10" |
4,5678∙10–3 |
2,7423∙10–5 |
6,5632∙10–3 |
3,2545∙10–5 |
|
4,5579∙10–5 |
2,2781∙10–6 |
1,9907∙10–3 |
8,5377∙10–4 |
3,4863∙10–3 |
|
6,3324∙10–6 |
4,6360∙10–4 |
4,6578∙10–7 |
3,2878∙10–6 |
5,5735∙10–4 |
|
3,7469∙10–6 |
7,4590∙10–5] T . |
Заключение
Предложен метод математического моделирования теплового состояния гидросистемы летательного аппарата. Математическая модель представляет собой систему дифференциальных уравнений в частных производных для углепластиковой композитной теплоизоляции и обыкновенных дифференциальных уравнений для элементов гидросистемы.
Решение прямой задачи теплового состояния элементов гидросистемы, а именно решение жесткой системы обыкновенных дифференциальных уравнений, проводили по методу Розен-брока и системы дифференциальных уравнений с частными производными методом Монте-Карло на основе вероятностного представления решения в виде математического ожидания функционала от диффузионного процесса.
Параметрическая идентификация математической модели теплового состояния элементов гидросистемы проводилась композицией метода наискорейшего спуска, метода Ньютона и ква-зиньютоновского метода Бройдена – Флетчера – Гольдфарба – Шэнно.
Построена математическая модель теплового состояния агрегата гидросистемы в негерметическом отсеке летательного аппарата и оценены доверительные интервалы каждого из искомых коэффициентов модели с использованием χ 1 2 -α распределения при доверительной вероятности β = 0,95.
Список литературы Идентификация математической модели теплового состояния гидросистемы летательного аппарата
- Воронин Г. И. Системы кондиционирования на летательных аппаратах. М.: Машиностроение, 1973. 443 с.
- Дульнев Г. Н., Тарновский Н. Н. Тепловые режимы электронной аппаратуры. Л.: Энергия, 1971. 248 с.
- Дульнев Г. Н., Польщиков Б. В., Потягайло А. Ю. Алгоритмы иерархического моделирования процессов теплообмена в сложных радиоэлектронных комплексах // Радиоэлектроника. 1979. № 11. С. 49-54.
- Николаев В. Н., Гусев С. А., Махоткин О. А. Математическая модель конвективно-лучистого теплообмена продуваемого теплоизолированного негерметичного отсека летательного аппарата. Прочность летательных аппаратов. Расчет на прочность элементов авиационных конструкций // Науч. - техн. сб. 1996. Вып. 1. С. 98-108.
- Гусев С. А., Николаев В. Н. Численно-статистический метод для решения задач теплообмена в теплозащитных конструкциях сотового типа // Сибирский журнал науки и технологий. 2017. Т. 18, № 4. С. 719-726.
- Миснар А. Теплопроводность твердых тел, жидкостей, газов и их композиций. М.: Мир, 1968. 460 с.
- Артемьев С. С., Демидов Г. В., Новиков Е. А. Минимизация овражных функций численным методом для решения жестких систем уравнений. Новосибирск, 1980. 13 с. (Препринт / ВЦ СО АН СССР; № 74).
- Ладыженская О. А., Солонников В. А., Уральцева Н. Н. Линейные и квазилинейные уравнения параболического типа. М.: Наука, 1967. 736 с.
- Соболев С. Л. Некоторые применения функционального анализа в математической физике. Издание третье. М.: Наука, 1988. 336 с.
- Gusev S. A. Application of SDEs to Estimating Solutions to Heat Conduction Equations with Discontinuous Coefficients // Numerical Analysis and Applications. 2015. Vol. 8, No. 2. P. 122-134.
- Himmelblau D. Process analysis by statistical methods. New York, Wiley, 1970. 463 p.
- Gill P., Murray E. Quasi-Newton methods for unconstrained optimization // Journal of the institute of mathematics and its applications. 1971. Vol. 9, No. 1. P. 91-108.
- Himmelblau D. Application Nonlinear Programming. Texas, McGraw-Hill Book Company, 1972. 534 p.
- Vladimir N. Nikolaev. Confidence Intervals for Identification Parameters of Heat Exchange Processes in Aircraft Instrument. Mathematical modeling of processes and systems. Compartments // Actual Problems Of Electronic Instrument Engineering: XV International Scientific and Technical Conference. (APEIE 2021). https://ieeexplore.ieee.org/xpl/conhome/9647431/proceeding Published in December 27, 2021. DOI: 10.1109/APEIE52976.2021.9647437. Novosibirsk State Technical University, Russian Federation. P. 539-542.
- Vladimir N. Nikolaev. Optimal Planning of a Flight Experiment During Parametric Identification of Heat Transfer Processes of the On-board Aircraft Equipment // 2022 XIX Technical Scientific Conference on Aviation Dedicated to the Memory of N.E. Zhukovsky (TSCZh). (APEIE 2022). Published in 23 June 2022. ISBN Information: INSPEC Accession Number: 21818057. DOI: 10.1109/TSCZh55469.2022.9802493. Moscow, Russian Federation. P. 39-42.


