Идентификация многомерных по входу стационарных линейных динамических систем

Самарская государственная академия путей сообщения

В статье рассматривается задача оценки параметров линейного разностного уравнения с многомерным входом при наличии помех наблюдения во входных и выходных сигналах. Эта задача отличается от стандартной задачи регрессионного оценивания, предложен новый критерий оценивания на основе отношения двух квадратичных форм, обобщающий стандартный метод наименьших квадратов и позволяющий получить состоятельные оценки параметров. Предлагается также численный метод определения оценок параметров линейных разностных уравнений, сводящийся к многократному решению линейных разностных уравнений.

Пусть имеет место стационарная линейная динамическая система, которая описывается следующим стохастическим уравнением заданного порядка с дискретным временем i = - 1,0,1

r                       d rj z.-Lb 0 m) z-m = LL a 0 mjj    (1)

m = 1                  j = 1 m = 0

У. = zi + 5(i), w.j) = x(j) + 5(j) (i), где ^1(i)— помеха наблюдения в выходном сигнале, ^(j)(i)- помеха наблюдения соответственно в j - м входном сигнале.

Применение классического МНК не позволяет получать состоятельные оценки параметров: в самом деле, использование классической процедуры МНК для определения параметров разностного уравнения приводит к минимизации среднего значения величины:

e ² ( b ^{( m} ) , a ^{( mj} ) ) =

r

У , - L b ^{( m} ) y _, m = 1

d r j

-У Y a ^{( m} j) wVL i — m

j = 1 m = 0

Такая постановка задачи не совпадает с обычной постановкой задачи в регрессионном анализе.

Пусть выполняются следующие условия:

• 1)    Множество _B ^~ , которому априорно принадлежат истинные значения параметров устойчивой линейной системы является компактом.

• 2)    Помехи 5 1 ( i ), 5 ^{( j} ) ( i ), j = 1, d статис-

• тически независимы и удовлетворяют следующим условиям:

E ( 5 1 ( i + 1)/ 5 1 ( i 0 ), . 5 1 ( i )) = 0 п.н.;

E (( 5 ) ² ( i + 1)/ 5 1 ( i 0 ), . 5 1 ( i )) = C 1 ( i + 1) < П <* п.н.;

E (( 5 1 ) 4 ( i )) <  П 1⁽¹⁾ п.н.;

E(5 ^a) ( i + 1)/ 5 ^a) ( i 0 ), . 5 ^{( j )} ( i )) = 0 п.н.;

E (( 5 ^{( j )} ) ² ( i + 1)/ 5 ^{( j )} ( i ₀), . 5 ^{( j )} ( i )) = C ^{( j )} ( i + 1) <  n ^{( j )} < * п.н.;

E (( 5 ^{( j )} ) 4 ( i )) <  п ⁰¹⁾ п.н., где e _— оператор математического ожидания.

• 3)    { x (1) , . x i ^{( d} ) } статистически не зависят от { 5 1 ( i ) } , 5'(i)}, j = Id.

• 4)    Вектор входных переменных и истинные значения параметров удовлетворяют условиям:

^N                                                                    П . Н .

• ^{— 1} Tz^T(h ^:C.x⁰⁾CzH T^d)(iTW(z^T(iV- -d(x^{d )

N   L ( z r ( i )•( x r ( i))  •   •( x r,   ( i))  )  ( z r ( i )•   •( x r,   ) ) ^ ^H

1               d                         d      N ^№ i = i 0

где

zr (i ) = (zi-1 . zi - r )T , xrj' ) = (xi j). xijrj^.

Представим уравнение (1) для всех i = 1,2 . n в векторной форме в виде системы линейных алгебраических уравнений ( i ₀ = 1 ) :

z = Zb 0 + Xa 0, где

Z = (zi zN ’T , z0

Z =

^ZN - 1

^Z 1 - r

^ZN - r

+ . + Y(d)(a 0d))Ta 0d)]= ^(b 0, a 0 ’ где:

^ 12 - средняя дисперсия помехи наблюдения

§ i ( i ) , ( n¹ j ’ ) 2 — средняя дисперсия помехи наблюдения ^^{( 1} ’ ( i ) ,

X =

1 - r

N - 1

x

( 1 ) N - r

⁽ d ’

( d )

N -1

( d ) x rd

x

( d )

N - rd

, (2)

1 (AsA γ ₂

σ ₁

.

b 0 = (b 01b 0 r ))T, a 0 =(a 01 ^-° a 0 d))T, a 0j )=(a 00 j’. a 0rjj ))T.

Однако, вместо z , Z , X наблюдается только случайно возмущенный вектор Y = ( y 1 y N ) ^T e R N и матрицы A Y и a w =^{( A} w 1 ^v"- ^a w ( _d ) ) , которые определяются

Тогда определим оценку

f ^b ( N -:1

V <5( N) J

неизве-

стных истинных значений параметров

f_ ’ « J

V a 0 )

из условия минимума суммы взвешенных квадратичных отклонений e ( b , a , i ) с весом to ( b , a ) , то есть из:

min to ¹ ( b , a ^{( 1 )} . a ^{( d} ’ ) u_n ( b , a ^{( 1 )} . a ^{( d} ’ )

^f b J e B                                              , (3)

v a )

(2), если вместо z, ^ y,, x(j’ > w,(j’. Таким i ii i образом, задача идентификации параметров (b0 ■ a0 )T сводится к решению стохастических алгебраических уравнений [1,2], определяемых значениями у, (Ау ■ AW) = AY,W, вероят- ностные характеристики которых описываются условиями 1 – 4.

Представим уравнение (1) в виде: y i =U ( - ) ■ W ■-■ W d d W b ⁰K 5 1 ( i ) - ^b 0 -< a 0° . - - rT a 0 d ’ ,

V a 0 )

где

B „ Ай¹'-Al e j

Введем следующую невязку:

e ( b 0 , a 0 , i H ( i ) -S b 0 -S T a 0^{1 1}-S da 0 d > .

Тогда из уравнения (2) и леммы 1.1 [1,2], получаем, что средняя дисперсия невязки равна:

1* KT-1 Nr ( 2(u              —2 I —2        I /'—(1) (1) V (1) I limN УE(e (b0,a0,i"= s + sb0b01 (s )(a0 ’ a0 + ^

N ^ro i = i 0

+    ^{( d} ’ я^{( d} ’ T a^{( d} ’ = CT2I1 + b^Tb + y⁽¹⁾(a⁽¹⁾ T a^{(1 )} +

. + V ) y0 0 ) a 0 U1 1 + b 0 b + Y \0 0 ) a 0 +, где

U N ( b , a ^{( 1 )} . a ^{( d} ’ ) =

Y - A y,W V

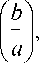
^{Y a}y , w

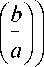
( • , • ) - скалярное произведение.

Утверждение 1. Пусть стационарная динамическая система с нулевыми начальными условиями описывается уравнением (1), и выполняются условия 1 – 4, тогда оценки

b ( N

V ° ^l ( N ) ^J

, определяемые выражением (3) при

N ^ _ro существуют и являются сильно состоятельными оценками, то есть:

f Ь (N_ ) J П.Н 7 . „J

V <$( N ) ) ^N >' - a 0 ) .

Доказательство утверждения 1. Рассмотрим функцию:

1 U n ( b , a ) = N -']T ( z i . +^ 1 ( i ) - ( z r. ( i ) + S T b -f ( x «( i ) ) ^T +S r 1 J a ^{( 1 )}- .

N                    i =1                                 ^{V                7}

-V ⁽ x d ' (< +S r d J a ^{( d} ) =

-1 У СЕ (A + zTHAb +        a⁽¹⁾ + d)^dad^d )-z T G'U-

= N 1\S1 (i) + zr (i)b0 + —1 (i)) a0 + — \xrd (i)) a0 zr (i)b i=1

-3 T b - V - (" - i ll' a ("-Э J a "I- — - ( x ,, ' - i ll' a ^{1 - 1} -3 T . a^1- T =

= N"1£ k. W-zT №-(-Ma(11- — -(x1- '(iljTS(d'- i=1

^-3 T b ^-3 T a ^{( 1 ) -} — ^-3 - a ^{( d ))} = v , +v 2 +v з , где:

~ b = b - b0,

~ ⁽ j ¹ = a ⁽ j ¹ - a 0 j ¹ .

v , = N -'f V ( i ) + b T 3 r 3 T b + ( a O' ) ¹ 3 „ 3 T a ^{( 1 )} + — + ( a ^{( d )} ) T 3 r , 3 T.a ^{( d} ) + + 2 b T 3 r 3 r i a ^{( 1 )} + — + 2 b T 3 r 3 r d a ^{( d} ) - 2 ^ ( i ) 3 - 2 ^ ( i ) ( 3 ^ a ^{( 1 )}- - — - 2 ^ ( i ) ( 3 г , ) T a ^{( d} ) + 2 ( a⁽" ) T 3 r 3 r a ^{( 2 )} + — + 2 ( a ^{( d - 1 )} ) T 3, - 3 - a ^{( d} )

в силу условий 2, 3, 4 удовлетворяет условиям леммы 1.2 [1,2] и, следовательно, равно 0.

Заметим, что f zi-151(i-1) :

. z i - 1 5 1 ^{( i - r} )

NN

N -1 1 b T 3 r z ( i ) ~ = N ^- 1 b T i = 1                                         i = 1

^zi - r 5 1 ^{( i - 1} )

^:               b .

z i - rU. ^{( - r )7}

Таким образом (4), можно представить в виде r2 слагаемых, каждое из которых в силу условий 2, 3 по лемме 1.2 [1,2] сходится к нулю. Аналогично можно доказать, что и все остальные слагаемые сходятся к нулю с вероятностью 1 при n > ^ •

Следовательно, п . н .     f b 1

v 3 >  0, ^v;

n >ю    v ^a 7

e B

N v 2 = N ^{- 1} 1

i = 1

7 ^b ~ ^{( 1 )}

T

X

X

и

П . Н .

N⁴U y ( b , a ) >  O 1² N

+ o 1² b^Tb + ( o ^{( 1 )} ) ² ( a ^{( 1 )} ) T a ^{( 1 )} + —

~( - )

V a  7

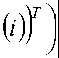
^~ b

— + ( o ^{( d )} ) ² ( a ^{( d} ^a ^{( d} ) +

~ ^{T b}

V a 7

H *

f ~ 1

- = ^{U ( b} , ^a ).

V a 7

Покажем, что решение задачи

~

V a

i(- ) ,

min ω

(b 1

~

NT v3 = 2N-11(-51(f1 zT(i))~41(i)(-«(i)) ~(1)- — 41(i)(xrd #~(d)

¹ ( b , a ^{( 1 )} — a ^{( d 1} ' u ( b , a ) , [ a J ^E B (5)

+

i = 1

+ b T 3 r z T ( ) ~ + ( a «У 3 „ z T ( i ) ~ + — + ( a<^{d 1}1 ^T 3 , d z: ( i ) b • + + b T = , ( х¹»^ , * . — + b T = , ( -;" ( i ' 1 ⁷ ~'- > + ( a ^(I> 1 T 3 , ( x r "( i 1 1 ⁷ ~» * + — + ( . ) 3 r i ( - rd > ( i )P a ⁽ - ) + — . ( a -) ' 3, ( x , d ⁾^ ~ ^{( d} >

Тогда из условия 2 по лемме 1.1 [1,2] получаем:

ПН -a²+a²bTb (о^г(¹)a(1) T '"     +fe( ^d ) q( ^d ) T «( ^d )

v i \ — о i + о i и и + у и , i a j a +. — + t o i i a i a

N ^^

существует и достигается в единственной

точке

I b 1

V ^a 7

f_^«i

V ^a 0 7

Рассмотрим следующую вспомогательную функцию:

V ( b , a , 6 ) = U ( b , a ) - 6>® ( b , a ^{( 1 )} — a ^{( d} ) ) , 0 e R 1 ,

V ( 6 ) = min V ( b , a ,6 ) ,

f-: 1

V a 7

~

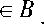
f b 1

~

^v ; e B V ^a 7

Из условия 4 следует:

Тогда

.

V ( b , a , 6 ) = O 1² +f- ’ 7 TH *f- ’ 7- 2 ^f H *f-' ⁰ 7 7 f b 7 - O 1² 6 + f-' 7 T X

V a 0 7     V a 0 J V V a 0 77 V a 7        V a 7

^v 2 =

~ ^{T b}

V a 7

H *

^f ~ 1

V a 7

f b 1

~

,

v- e B

V ^a 7

.

Слагаемое i 1 f-6i(<)zT(I)’ "^i)(x^i)fa'L-. -61(i)(-Г,'(1 )Г~1 d’

^N i = 1

^f H zz ⁺ ° 1² I r ^{- 6} ° 1² I r ^                   H zx ( , )                "

. H X- ">Г" "!"! " X-^>х-+ ° ⁽ ") ’- bd 1 -’ ⁶ °    bb1

xfb 7

V ^a 7 ^,

если

H *

HZZ

^H zx ( d )

.

к ^H X ^{( d} ) Z

H X ^{( d} ) X ^{( d} ) 7

Дифференцируя V ( b , a , б ) по

f b I

к a 7

и при-

отрицательна на интервале ( — от , X min + 1 ) , отсюда следует, что V ( б ) = 0 на интервале ( —от , X min + 1 ) имеет не более одного корня.

Нетрудно убедится, что б = 1 является корнем уравнения V ( б ) = 0 и 1 < X min + 1.

Тогда из (6) непосредственно следует справедливость (5).

равнивая производную к нулю, получим:

f a §=

Введем следующий

вектор

f H zz + ^ 12 1 , — 9a 1² 1 ,

H zx ( d )

A1

X

к         ^Hx ( , ) z

^H X ( d >  X t d >  ^{+( СТ ( d} ) ) ¹ d + 1

9 ( a ^{( d} ) ) 2 i d J

f

X H * к

0 - к a 0 77

Тогда

f b

V ( 9 ) = a + ^{b 0}

I ^T

H *

к a 0 7

f--1

к ^a о 7

— a ₁2 9 —

^H * к

' ^b 0

X

f H zz + ^ 1² 1 , — 9a 1² 1 ,

X

к         ^Hx ( , ) z

f

X H * к

0 - к a 0 77

H zx ( d )

x1

X

^H X I d >  X I d >  ^{+( a ( d} ) ) ¹ d + 1

9 ( a ^{( d} ) ) 2 i d J

Если X min - минимальное характеристическое число регулярного числа форм

H ZZ ^{+ a} 1 ⁱ, [

^Hzx ( d )

—

к   ^HX ( d ) Z

i H , ( d ) , ( . , +^{( a}“ ' 1,, . 1 7

^{f a} 1^{2 i},

– θ

к ⁰

0 ! -

0 I

0 I — ( a ^{( d} ))2 1,

,

d d ^{+ 1} 7

то, следовательно, X min >  0, и функция V ( б ) на интервале ( —от , X min + 1 ) непрерывна и

dV ( 9 ) _    2

= — a d θ      ¹

■ b I ^r

^f 0 2 I ,

0 I

b

—

a

( a ⁽ d ^{1) 2} L. +J

a

( 1 - b \ a ⁽¹⁾... a ^{( d} ) ) = u A Y , W = ^{( —} Y ! A Y , W ) ,

D *

, {

и

матрицы

r dd+1

, 1 + 1

dd + ^{1 {}

σ 12	0	0	” '	0
0	σ 12 I r	0		0
0	0	0		( a1 d 7 1 , d + 1

,

то (3) можно записать в виде:

. u a y w " A Y W u min          Y , W Y , W

~                        T r^*

“ ^E B ^c R , +1+ 1 + ^ ,d + 1       u D u

,

^где A Y,W A Y,W >  ⁰ .

Для конкретной выборки объема N нахождение корня уравнения V N ( б ) = 0 (эти корни имеют те же свойства, что и для V ( б ) = 0) можно записать в следующей форме:

^б N = ^X min ^{( N} ) A TT W A Y , W ⁽ D )

–

минималь-

ное характеристическое число пучка квадратичных форм, определяемых A Y _W , A Y , _W и D *. Но D * >  0, поэтому рассмотрим [3, С. 281]:

^A min ⁽ N ^)[ A Y,W A Y,W   ⁹ D ^] =

1 N

•

^A max ⁽ N ) ⁽ A Y,W A Y,W ) D ^.

Известно[4, P. 452], что:

1                   П . Н .

У¹ o* l N ^>от

A Y , W A Y , W   D

J       ^/umax

, 1 T у , lim A Y w A y w I D N ^от N ’ ’ 1

λ min

1 _T lim    A Y , W A Y , W

N ^от N

i—1

.

Так как нахождение

λ min

1 T lim A N ^® N  ^w

A Y , W

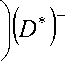
можно интер-

претировать как определение корня уравне-

1       П . Н .

ния V ( б ) = 0, то — ⁶_N ^ 6 .

N   N ^®

Далее параметры можно определить, если ввести следующую вспомогательную функцию:

V n ( - , a, 0 ) = Y^TY - 5 2 0 - 2 ( y^tA y ! Y^TA_W f b ^J +

V a J

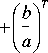
¹ A Y A Y - 05 1 I r I A T A w I -

AY AWd

X

d )

A W d A Y      I         I I A W d A W d    ⁰⁵   ) I r_d +1

—

N

f a T y J П . Н .

^

V a W y J N ^”

^f H ZZ ^{+ 5} 1 I r ^{- 05} 1 I r  ^-                 H ZX ( d )

I

V        H X ( d ) Z        H H X ( d ) X ( d )+^{( 5 ( d f)2} I r d + 1 - ^{0 5 ( d ))2} I r d + 1

f b 1

X

^“

H *

X

X

[- - 1

V a J

Дифференцируя V_n ( b , a , 6 ) по - и a и приравнивая производную к нулю имеем: fA Y A y - 05 1 I r l A TT A w J-l        A T A wd       '

i:::::i::i4-i::::::::i::::::::

V A W d A Y    I - :-: A W A - ^{05 ( d} O² I d +i j

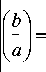
V a j

f_ ^b « 1 V a 0 J

Из единственности решения (6) и (7) и последнего выражения следует [5, P. 178], что

оценки стремятся к истинным значени-

ям

f b ( N ) J П . Н .f . „ J

V <$ ( N ) J ^N >'_k a 0 J

Для получения численного метода вычисления оценок параметров из критерия (3) рассмотрим функцию:

V n ( b , a ,0 ) = U n ( b , a ) - 0ю ( b , a ) ,

V n ( 0 ) = min V n ( b , a,0 ) b

I -Ie b

V a J

тогда:

I- ¹ 1

V a W y J ,

f

V n ( b , a ,0 ) = Y^T V

f b J ^T

V a j

T

Y , W

^Y   a y , W

i : ii

V a J J

- 0 ( 1 + b^Tb + y ^{( 1 )} ( a ^{( 1 )} ) ^T a ^{( 1 )} + ••• + y ^{( d} ) ( a ^{( d} ) ) ^Ta ^{( d} ) =

V n ( 0 ) = Y T Y - 5 12 0

^f к J

TTY

V A w¹ J

X

= Y^TY - 2( y^tA_y 1 Y^T A

¹ w :(-' J

V a J

—

bT

⁰ +;

V a J

X

X

¹ AY A y - 05 1 I_r A AAA^ i-

5 д

A Y A W_d

X

a Y A y - 0 I r          A T A w ( 1 )

" AW W Ar ^l A W W Aw ^O^{- 0/111} I m

V A

V    A W d A Y

A W d A W d - ^{0 ( 5 (} d ^{) )2} I d + 1 ^J

A W ( d ) A r    1         A W ( d >  A_w ( ! >

I          ^AY A_W ( d )

I           A W (1) ^AW ( d )

1 A W ( d ) A W ( d ) - ⁰/ ⁽ d ) I r d + 1

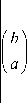
X

I- A ¹ J

V a W y J

и неизвестные параметры могут быть определены из уравнения (7).

Тогда, очевидно

Дифференцируя V_n ( b , a , 6 ) по - и a и приравнивая производную к нулю имеем:

f A Y A r - 0 1 , I A Y A wv.

A WW 0 A Y”!

A T A w d

A _w ( I ) A _w ( d )

1 N

aya y ⁰⁵ 1 i r A t aw,^ 1

I   AT”!

T

V A W d A Y      I          I

T

A Y A W d

A W d A W d - ^{0 ( 5 (} О I r d + 1

V A W w A r   I a W m a w O)

откуда

- I a W w a w W- 0/ ^{( d} ) I r d + 1

b

a

A _T_ y J

^T I A w¹ J ,

X

Далее,

V n ( в ) = Y T Y - 0 -

f A Y A Y - 0 I r A W ( 1 ) A Y

T

A Y A W ( 1 )

A Y^T A

W ^{( d} )

X -1

I r

V N ( в ) =

—

1 +

b

a

Т

r , r 1 +1

/        r , +1

⁰ r„ +1

⁰ r +1, r d +1

A W ( 1 ) A W ( d )

X

l

r , r d +1

0 ^T

Y ^{( d} ) I r

<- 1

l A W ( d ) A Y

X

A W ( d ) ^AW ( ! )

f-ATY-J lAWyj .

A W ( d ) A W ( d )

0Y ( d ) + 1 J

Тогда на интервале ( да A min ( N )) V n ( 0 ) имеет не более одного корня, если он существует, V_N ( 0 ) >  0и, следовательно, V N ( 0 ) > 0 V 0 e ( - да ,0 ) (матрица

Имеет место следующая лемма.

Лемма: для функции V N ( 0 ) , связанной с задачей (3) существует следующее утверждение:

1) Все корни уравнения V N ( в ) = 0 не от-

IN

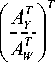
A Y A Y I A Y A W ( 1 ) I - I A Y A W ( d )

TT    T

A W ( 1 ) A Y I A W ( 1 ) A W ( 1 ) I I A W ( 1 ) A W ( d )

- 1

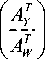
A W ( d ) A Y

A W ( d ) A W ( ! )

A WT ( d ) A W ( d )

рицательны;

2) Уравнение (10) на полусегменте [ 0, A min ( N )) имеет не более одного корня 0 ( N ) , где A min ( N )- минимальное собственное число регулярного пучка форм, то есть наименьший корень уравнения:

det <

A Y A Y ! A Y A W (1) I A W Y A T U W « A W ;)":

a y A W ( ^d )

A W ( 1 ) A W ( d )

—

A W ( d ) a y 1 A W ( d ) a w (o I

A W ( d ) A W ( d )

- 0

I r 0 Y r + 1	0 r , Г ’+ 1 у(1)/ . /        r 1+ 1	1 е -1— 1	, 1 —1 -+	0 r , r d + 1 0 r 1+1, r d +1
0 Y r d +1:	T 0 r + 1, r d + 1	1 • 1	1	( d /        r d + 1

^ = 0

3) Существование корня 0 ( N ) на полусегменте [ 0, A min ( N )) является необходимым и достаточным условием существования и единственности решения (3).

Доказательство леммы. Функция V N ( 0 ) на [ 0, A min ( N )) непрерывна, к тому же A min ( N ) >  0 как собственное число неотрицательной определенной матрицы.

идемпотентная).

Отсюда вытекает справедливость утверждений 1, 2 и достаточность 3. Необходимость 3 ⁰ вытекает из экстремальных свойств регулярного пучка форм [3].

Утверждение 2. Пусть выполняются все условия утверждения 1 , тогда с вероятностью 1 при n ^ю существует корень 0 ( N ) e [ 0, A min ( N ) ] и единственная оценка (9), которая является одновременно решением задачи (3) и b(N ) _N _^ > b 0 п. н.;

<2( N ) - N ^да ^ a ⁰ п.н.

Доказательство утверждения 2 следует из утверждения 1 и леммы.

На основании утверждения 2 предлагается численный метод, который позволяет: ответить на вопрос существует ли единственная оценка b ) ( N ), a ( N );

определить начальное приближение, гарантирующее сходимость итерационного процесса к единственной оценке b ) ( N ), a ˆ( N );

вычислить с любой наперед заданной точностью оценку b > ( N ), <$( N );

Утверждение 3. Пусть последовательность { 0 '( / ) } определяется следующим алгоритмом:

Шаг 0.

0 '( 0 ) = 0;

Шаг 1.

Процесс вычисления заканчивается, если выполняется условие

+ 0,(i -1))

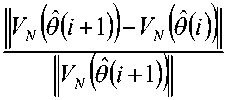
< 5

Шаг 2. Вычислить - ( N,0' ( i ) ) , a ( N,0' ( i ) ) из системы линейных уравнений (9);

Шаг 3. Вычислить

где δ - априорно заданная точность оценок.

Это утверждение непосредственно вытекает из метода Ньютона:

V N ( 0 ( i ) ) = Y T Y — 0 -

AS

A TY к AwY V

b\N ,0( i ) )

T     A / X \ к a(N ,0'(i)))

⁰ ( i + 1 ) = ⁰ ( i ) - VN^

VN (0(i )

Шаг 4. Проверить условие V_N ( 0 '( i ) ) < 0 . Тогда если уравнение V_N ( 0 '( i ) ) = 0 имеет

корень 0 1 ' ( N ) е [ 0, A _min ( N )) , то последовательность 0 '( 0 ),6 ? ^, ( 1 ), ^6 ? ( 0 ) - конечна и 0 ( 0 ) е 0 ₁ ' ( N ) , A _min ( N ) ) , в противном случае последовательность бесконечна.

Доказательство утверждения непосредственно следует из леммы.

Этот алгоритм позволяет определить начальное приближение 0 ( 0 ) , необходимое для дальнейшего применения метода Ньютона или определить, что корень 0 1 ' ( N ) не существует.

Утверждение 4. Пусть существуют ( 0 ) е 0 '( N ) , Л _т„ ( N ) ) ^, тогда l™ ^{0 i} ) ⁰К ^N ) ^, lim b ( i,В ( ) ) = b ( N ) lim a ( i , 0 ( i ) ) = a ( N ) где i ^w                    ^, i ^w                     ^,

0 ( i ) , b ( i,0 ( i ) ) и a ( i,0 ( i ) ) определяется совместно со следующим алгоритмом:

Шаг 1. Вычислить - ( N,0 ( i ) ) , a ( N,0 ( i ) ) из системы уравнений (9);

Шаг 2. Вычислить

Обоснованность использования метода

Ньютона следует из того, что V N ( 0 ) - непрерывна для V 0 е [ 0, Z _min ( N )) , V N ( 0 ) <- 1для V 0 e [ 0, A m_m ( N )) и

• •

V N

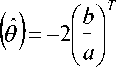
A Y ^TA Y

A W ( 1 ) A Y

A_W ^{( d} ) A Y

I r

T

⁰ r , r 1 + 1

T

0 r , r_d + 1

I r

T r, Г] +1

T r, rd +1

a y A W ( 1 )

A W ( 1 ) a w ( 1 )

A W ( d ) A_W ( ^! )

⁰ r , r 1 + 1 ⁽ⁱ⁾^"7 ^Y r 1 + 1

0 r , r 1 + 1

^Y        Г 1 + 1

⁰ r,r d + 1

I   ⁰ r 1 + 1, r d + 1

X

0T r1+1, rd+1

у ⁽ d )/   ,

I ^Y        r d ⁺¹

A Y A W ⁽ d )

A W ( 1 ) A_W ( d )

A W ( d ) A_W ( d )

0 r , r_d + 1

1 0

0 r 1 + 1, r d + 1

0 ^T I I r⁽ d )/

0 r 1 + 1, r d + 1 I I ^Y I rd + 1

X

xf-' 1

к ^a V

< 0

0 ( i + 1 ) = ( 1 + b ( N , 0 ( i ) ) T b ( N , 0 ( i ) ) + у ^{( 1 )} [ a ^{( 1 )} ( N , 0 ( i ) ) T a ^{( 1 )} ( N , 0 < ()) + - _ + у ^{( d} ) [ a ^{( d} ) ( N , 0 ( i ) ) T a ^{( d} ) ( N , 0 ( i ) ) ) 1 Y ! + 0 ( i ) [ b ( N , 0 ( i ) ) T b ( N , 0 ( i ) ) + + у ^{( 1 )} [ a ^{( 1 )} ( N , 0 0) )]" a ^{( 1 )} ( N , 0 ( i ) ) + - + Y ⁽ d ) [ a ⁽ d ) ( N , 0 0) )]" a ⁽ d ) ( N , 0 ( i ) ) ] -

/    -T"   \ / * X I

-f A"Y)| b )l к AWY Л a ]/ ;

Шаг 3. Перейти к шагу 1.

для V 0 е [ 0, a . . ( N )) .

На основании предложенного численного алгоритма создано программное обеспечение, позволяющее получать оценки параметров с наперед заданной точностью.

В качестве примера рассмотрена стационарная динамическая система, которая описывается следующим линейным разностным уравнением:

r z. - У-

i              0i m=1

:-j

d   rj

(mj) (j)

m =^^a0 xi-m , j=1 m=0

При d = 2 , r = 2, r₁ = 1, r₂= 2 имеем

• 0)       .//2), _r0). J^0,1), _r0) .^LJ²). J0^,2)

^zl = zl-1 * ^b0 ⁺zi-2 * ^b0 ⁺xi * a0 ⁺xi-1 * a 0 ⁺xi * a 0 ⁺ + xi_T a_:) + xi^- a 0²'²)

Векторы входных сигналов Xi = {х⁽¹), x⁽²⁾} и векторы помех Si = {fi^, f‘^2:, f₁(i)} заданы с помощью генератора случайных чисел:

xi⁽¹⁾ = rnorm (N ,0,0.2)

xi⁽²⁾= rnorm (N ,0,0.2)

f W = rnorm (N ,0,0.1)

fi^ = rnorm (N ,0,0.1)

f (i ) = rnorm (N ,0,0.15)

В табл. 1 приведены значения оценок параметров, полученные в результате тестирования на основе предлагаемого численного метода (при числе экспериментов N = 120).

Также получено значение среднеквадратичного отклонения сигнала Z_i от Z^ˆ_i :

N

Z⁽Zi- Z.T

'2    /=1

CT = —---------,

N -1

^T^ = 0,018,

где Z^ˆ_i - значения выходного сигнала, полученные по рассчитанным оценкам коэффициентов b)(N,()'(i)), <я(N,()'(i)).

Таблица 1. Сравнение полученных оценок параметров с истинными значениями.

Параметры	Истинные значения	Полученные оценки
b (1)	1	1,018
b(2)	-0,5	-0,523
a (0,1>	0,5	0,501
a(1J)	0,4	0,381
a(0,2)	0,3	0,28
a(1,2)	0,6	0,579
a(2,2)	0,2	0,203