Идентификация модели солнечной батареи

Необходимость сокращения сроков разработки и повышения эксплуатационных характеристик систем электроснабжения (СЭС) космических аппаратов (КА) выдвигает на первый план задачу создания эффективных методов проектирования подобных систем. В большинстве случаев правильный выбор структуры СЭС КА и согласованный режим работы источников электроэнергии позволяют повысить удельные энергетические характеристики на 40% [1].

В настоящее время в качестве первичного источника электроэнергии в СЭС КА наиболее широко применяются солнечные батареи (СБ). В статье рассмотрены вопросы математического моделирования характеристик СБ в диапазонах освещенностей и температур, соответствующих реальным условиям ее эксплуатации.

Энергоотдача СБ во многом зависит от структурной схемы СЭС КА, схемотехнических решений силовой час ти импульсных преобразователей и способа формирования управляющего сигнала. Оценка энергетических возможностей СБ для каждого конкретного случая определяется точностью математической модели при любом сочетании значимых факторов.

Наиболее распространена теоретическая модель воль-тамперной характеристики (ВАХ) солнечного элемента (СЭ), полученная на основе схемы замещения с сосредоточенными параметрами [2; 3]:

I_H = 1 _ф - I _oн {exp[ eU ^н + I ^н R ^п ) ] - 1} - U^ ,   (1)

H Ф UH                                     ^,

AkT        R ш где IH - ток нагруженного СЭ; IФ - фототок, или ток короткого замыкания СЭ; IOH - обратный ток насыщения; UH - напряжение на СЭ; Rп - последовательное сопротивление (тела полупроводника и контактной сетки СЭ);

R _ш - индуктивное сопротивление; k - постоянная Больцмана; T -абсолютная температура СЭ; e - заряд электрона; А - эмпирический параметр ВАХ, получаемый при сравнении теоретической и экспериментальных кривых и принимающий значения от 1 до 5.

Очевидно, что требуемая точность описания ВАХ обуславливает точность входящих в формулу (1) зависимостей, причем Rп и Rш могут быть получены экспериментально, а А - только косвенно, вычислением. Если членом —H можно пренебречь (Rm достигает несколь-R ш ких КОм), то сопротивлением Rп , являющимся функцией температуры, пренебречь нельзя даже при условии, что IHRп << Uн . Очевидна также большая чувствительность (1) к эмпирическому параметру А.

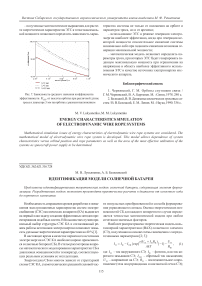
При экспериментальных исследованиях наиболее удобно представлять ВАХ по трем характеристическим точкам: холостого хода, короткого замыкания и максимальной мощности (рис. 1). Эти точки уверенно регистрируются приборными методами, однако не учитывается конкретная схема замещения, а исследуемый объект выступает как источник с нелинейной ВАХ, то есть имеет место формализация представления кривой.

Рис. 1. Представление ВАХ СЭ по трем характеристическим точкам

С учетом эмпирического характера (1) и необходимости проведения соответствующих исследований рассмотрим формализованные выражения, аппроксимирующие кривые подобного вида, исходя при этом из того, что наилучшее приближение к ВАХ СЭ, как к и-^-переходу, можно реализовать экспоненциальной функцией. В общем виде экспоненциальные модели можно записать в виде

I H = I _кз [1 - e f ^{( U н )} ] ,                 (2)

где f (U _H) - функция текущего напряжения и параметров характеристической ВАХ, равная ln(1 - i )

f ^{( U} H ) ^{_ ( U} H ^U XX )    Z. _n,         (^)

U xx ( j - 1)

где параметры i и у определяют относительное положение точки максимальной мощности, причем i _ 1опт ; j _ Uопт ;.

^J кз             XX

Представление ВАХ СЭ через формальные параметры i и j приведены в работе [4], где однако авторы не учитывали влияние R _п и не включили в описание параметров зависимости температуры и освещенности (указаны лишь пределы их изменения). Исследования, проведенные авторами, показали, что хотя аппроксимирующая кривая проходит через точку с координатами i и j, но ее оптимальная точка не совпадает с заданной.

Таким образом, задача сводится к идентификации указанной характеристической точки. Для этого вводится дополнительное условие, которому эта точка удовлет-dP                 dI             iI воряет: -—     _ 0 или, ——     _--.

dU            dU         jU н Uу_Uопт                н Uh _Uопт     J XX

Опуская промежуточное доказательство, отметим, что в экспоненциальной модели по выражению (2) нами использовалась подстановка f (Uн) _

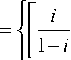
ln(1 - i ) If ^ . ^ln j Д ^U XX ^j

- 1 + ln(1 - i Hx

ln( U H U XX )

x---------------.

ln j

В характеристических точках кривой I _кз , U_X , i , j зависимости от освещенности и температуры описываются следующим образом:

Uxx _ (АС + А - A31)Nпос, cS^ „(1 + At)

кз _--- ,

A4 Nпос j _ Аб - CA7et - At, i _ A0 - cA11 e'"* - A3t,

( Вт )

где c -удельная мощность излучения I —- ; t -темпе-I А , ратура(°С); S - площадь СБ м2; Руд - удельная электрическая мощность СБ; Nпос - количество СЭ, соединенных в СБ последовательно; А1... А13 - эмпирические безразмерные коэффициенты аппроксимации.

Выражение (2) с подстановкой (4)...(8) справедливо для следующих диапазонов температур и освещенностей:

c _ 0...1400^ 2 , t _- 90... + 80⁰C , м

Руд _ 100...140^2. м для образцов СБ с

Поскольку при экспериментальных исследованиях регистрировались характеристики не отдельных СЭ, а минимальных сборочных единиц - модулей, то и выражения (4)...(8) описывают СБ, состоящую из идеальных (не имеющих технологического разброса) одинаковых СЭ, ВАХ которых связаны аффинным подобием с результирующей ВАХ, что при экстраполяции на СБ большой площади обеспечивает удовлетворительную точность.

Проведем идентификацию теоретической модели, считая полученную формализованную модель исходной точной. Для теоретической модели выразим эмпирический параметрА через известные зависимости

A _

UXX e kT ln I I^- +1 IIOH

для чего воспользуемся зависимостью обратного тока насыщения от температуры

I OH = 5 1 exp[ B 2 ( T - 273)] —.         (10)

N пос

Значение Rп определяется из условия прохождения теоретической кривой через точку с координатами i и у формализованной. Разница абсцисс кривых при I = Iопт (при одинаковых Ти Л), описывающих ВАХ «идеального» диода и реального СЭ, представляет собой падение напряжения на Rп . Таким образом, зависимость можно аппроксимировать выражением

R _п = B ₃exp[ B ₄( T - 273)] —.        (11)

N пос

Значения коэффициентов аппроксимации в выражениях для СБ с P = 120 ^^Т следующие:

^д м ²

А 1 = 5,46 - 10 ^{- 5} ;

А 2 = 0,550 8 ;

A 3 = 2,16 - 10 ^{- 3} ;

А ₄ = 2,298 - 10 ^{- 3} ;

А = 1,762 - 10 ^{- 3} ;

А = 0,782 ;

А 7 = 7,142 - 10 ^{- 6} ;

А = 1,96 - 10 ^{- 2} ;

А = 3,15 - 10 ^{- 4} ;

Аю = 0,896 ;

А 11 = 7,142 -Ю^{- 6} ;

А ₁₂ = 2,05 - 10 ^{- 2} ;

А ₁₃ = 2,35 - 10 ^{- 4} ;

5 1 = 1,14 - 10 ^{- 4} ;

5 2 = 3,43 - 10 ^{- 2} ;

5 ₃ = 4,2 - 10 ^{- 5} ;

5 4 = 9,54 - 10 ^{- 3} .

Таким образом, идентифицированная теоретическая модель (1) с подстановками (6) и (9)...(11) также содержит элемент формализации, поскольку реальные СЭ по своей сути являются элементами с распределенными параметрами. Однако для практического расчета эта модель приемлема, так как разница в значениях мощности, вычисленной по формализованной и теоретической моделям, не превосходит 1,5% в диапазоне от холостого хода до короткого замыкания, следовательно, указанная формализация допустима.