Идентификация, основанная на случайном кодировании

Следующая модель является стандартной в телекоммуникации. Имеется множество ^ = {и} состоящее из М сообщений и, каждое из которых может быть выбрано с одинаковой вероятностью для передачи по каналу связи. Для того чтобы передать по каналу сообщение и, потребуется передать посылку длиной log2 М бит. Для этого придется использовать канал

1/С log2 М раз, если пропускная способность канала - С бит на одно использование канала. При этом достаточно длинное сообщение будет получено правильно почти наверное.

В 1989 году Алсведе и Дюк [2] предложили рассмотреть другую модель, которая называется задачей идентификации сообщений. В этой задаче предполагается, что получатель (приёмник) ожидает лишь одно сообщение и, которое ему интересно. Отправителю (передатчику) ожидаемое сообщение и не известно. Приняв очередную посылку, получатель

«Московский физико-технический институт (национальный исследовательский университет)», 2022

должен решить, передавалось ли ожидаемое им сообщение и или нет. При этом допускаются ошибки принятия решения первого и второго рода. Алсведе и Дюк [2] показали, что при сколь угодно малых вероятностях ошибок в принятии решения существует процедура идентификации, которая для достаточно длинного сообщения требует использовать канал лишь

1/С log2 log2 М раз. Говорят, что такая процедура достигает идентификационной пропускной способности и назывется оптимальной. Выигрыш достигается за счет того, что для идентификации не нужно передавать все сообщение длины log2 М, а достаточно передать лишь его короткий «признак» длины log2 log2 М.

Кроме того, в [2] показано, что без потери эффективности задача идентификации по каналу с шумом может быть разделена на задачу идентификации (по бесшумному каналу) и задачу передачи признака сообщения по шумящему каналу. В связи с этим мы займемся собственно задачей идентификации, т.е. будем считать канал бесшумным с пропускной способностью С = 1.

Интерес к идентификации возобновился с появлением концепции Интернета вещей (1оТ). Предположим, что каждый из огромного числа М объектов 1оТ имеет свой идентификатор и Е U. Центральный узел для установления связи с объектом и посылает по сети признак идентификатора и. С помощью процедуры идентификации объект и принимает вызов, остальные объекты отклоняют вызов с большой вероятностью. В этом примере идентификация позволяет значительно сократить длину передаваемого запроса. Кроме того, задача идентификации тесно связана с задачей аутентификации [3], применяемой на практике, а также с другими задачами [4], что также вызывает интерес к идентификации.

Хотя возможности идентификации показаны теоретически в работе [2], задача построения практически реализуемых процедур идентификации для сообщений конечной длины с приемлемой сложностью остается открытой. В работах [2], [5], [4] предложено строить про-ЦСДУРУ идентификации на основе кодов, исправляющих ошибки. Конструктивная процедура идентификации Верду-Вэя, основанная на каскадировании двух кодов Рида-Соломона, предложена работе [5] и рассматривалась в работах [6], [7], [8] и других. Процедура Верду-Вэя является асимптотически оптимальной. Однако в [6] показано, что сложность процедуры Верду-Вэя очень велика для практических применений, т.е. для сообщений конечной длины, поскольку требует работать с конечными полями больших размеров. Возможность применения для идентификации кодов Рида-Маллера исследовалась в [9].

В настоящей работе предлагается оптимальная процедура идентификации на основе случайных линейных кодов. Показано, что эту процедуру можно упростить применяя генераторы псевдослучайных последовательностей.

2.    Идентификация с помощью кода

Мы будем рассматривать линейный (n, k, d)_q код С длины п, размерности к, имеющий кодовое расстояние d в метрике Хэмминга, над конечным полем F^, г де q является степенью простого числа. Обозначим порождающую матрицу кода через

G = (д(1), д(2),..., д(п)), где д(г) обозначают столбцы матрицы. Тогда кодовыми словами являются векторы с = (ci,..., сп) = uG, где и Е F^ - всевозможные векторы сообщений.

2.1.    Процедура идентификации

Передача. Для того чтобы передать идентификатор (сообщение) и, кодер вычисляет слово с = uG Е С. затем выбирает равномерно случайным образом индекс г Е [1,п] и передает по каналу идентификационное слово состоящее из случайно выбранного индекса г и г-го признака сг идентификатора и. Длина идентификационного слова w в битах nw = log n + log q.

Здесь и далее log = log2 означает логарифм по основанию 2.

Декодер принимает по бесшумному каналу слово w = (г, Сг) и должен решить, передавалось ли ожидаемое им сообщение и' или нет. Для этого декодер вычисляет слово С = и' G Е С и сравнивает его компоненту Сг с принятым признаком а. Ес ли с І = а, то считается, что принято омсидаемое сообщение, т.е. что и' = иг. Иначе, т.е. если с ' = с', считается, что и'_г = и_г, и сообщение отвергается.

Вероятность ошибки декодера l-ro рода, т.е. вероятность отвергнуть (пропустить) ожидаемое сообщение, обозначается через Ai, а вероятность ошибки 2-го рода, т.е. вероятность принять ложное сообщение, обозначается через A2.

2.2.    Анализ процедуры идентификации

Из описанной процедуры идентификации с помощью кода немедленно следует, что в случае бесшумного канала вероятность пропуска Ai = 0.

Заметим, что декодировать код С в обычном смысле не требуется ни кодеру, ни декодеру. Даже полностью кодировать сообщение и в кодовое слово с не нужно, требуется вычислить лишь один символ Сг, т.е. скалярное произведение Сг = (и, д^(г)).

Вероятность A2 ложного принятия оценим следующим образом. Слова с и с' (n, k, d^q-кода С отличаются по меньшей мере в d позициях г, а совпадают, т.е. С = Сг, не более чем в n — d позициях. Поскольку ложное принятие происходит при совпадении с' = Сг, получаем, что для любой пары сообщений и' = и выполнено а2 6 d =! — ■ n       n

Скорости идентификации определяется как log log \U |   log k + log log q

Ri = --------- = —------:-----.                          (4)

n_w        log n + log q

Вероятность A2 ложного принятия сообщения может быть уменьшена [8] путем передачи нескольких, скажем I, идентификационных слов шг1 ,шг₂ ,..., Wi_e. Декодер принимает сообщение, если оно принято для каждого из I слов w^, j = 1,...,1. При этом новая вероятность ложного приема становится равной

A2 6 (1 — n)'.

Процедура идентификации с помощью последовательности кодов С достигает идентификационной пропускной способности [2] и называется оптимальной, если при соответствующем возрастании параметров кода выполняются следующие условия [5]:

^  ■ о,

log n log k ___^ 1

log n , означающие, что для бесшумного канала скорость идентификации стремится к пропускной способности, равной 1, Ri —> 1, а также d -1

> 1, n т.е. вероятность ложного принятия сообщения A2 —> 0.

Определение 1. Последовательность (n, k,d)_q-Kop, ов С, удовлетворяющая условиям (5) -(7), называется оптимальной для идентификации последовательностью кодов.

Напомним, что для целого q > 2 и ж Е [0,1] функция q-ичной энтропии hq(ж) определяется как hq (ж) = ж logq (q - 1) - ж logq (ж) - (1 - ж) logq (1 - ж) .                   (8)

В работе [5] указано, что использование q-ичн ого (n, Rn, 5n)_q ко да С, асимптотически при n —> то достигающего границы Варшамова-Гилберта:

R = k/n 6 1 - hq(5),                                 (9)

позволяет получить оптимальную процедуру идентификации. В следующем разделе для построения такого кода предлагается использовать случайный код.

• 3.    Использование случайного кода для идентификации

Построим случайный линейный (n, k,d)_q код С над полем F_q. Для этого возьмем случайную порождающую матрицу кода

^G = (д^д^^2, ... ,д⁽¹⁾⁾ = (д^) ,                             (10)

выбирая элементы д^ матрицы G случайно, независимо и равномерно из поля Fq. Известно, что случайный код С с большой вероятностью асимптотически достигает границы Варшамова-Гилберта.

Теорема 1. Пусти 5 Е [0,1 - 1 /q) и 0 < Е <  1 - h_q (5). Тогда с вероятностью Р = 1 -q^^¹ случайный (n, k, d)_q Ktid С имеет скорость

R = k/n >  1 - h_q (5) - е,                              (11)

и относительное расстояние d/n не менее 5.

Доказательство может быть найдено, например, в [1].

Теорема 2. Процедура идентификации, основанная на случайном коде С, является асимп-тотичеки оптимальной с вероятностью 1, т.е. почти наверное.

Доказательство. При q —> то граница Варшамова-Гилберта (9) переходит в границу Синглтона R = 1 - 5. Из (11) получаем, что для любого е > 0 при достаточно больших длинах n скорость R случайного кона, с вероятностью Р = 1-q^-en+1 нс менее R >  1-5- е - y(q). где у(q) —> 0 при возрастании q. Поскольку параметры случайного кода совпадают с параметрами кода в [5, Theorem 3], далее наше доказательство совпадает с доказательством в [5, Theorem 3], где показан такой выбор растущих параметров последовательности кодов, который обеспечивает выполнение условий (5) - (7). Параметр е выбирается таким образом, что Е —> 0, но при этом Р = 1 - q^^-^¹ —> 1, что завершает доказательство.

Теорема 2 показывает асимптотическую оптимальность процедуры идентификации, основанной на случайных кодах. Но для практических приложений интересно поведение этой процедуры для конечных значений параметров. Покажем на примере, что и для конечных значений параметров кода эта процедура может представлять интерес.

Пример 1. Пусть q = 210 = 1024, n = q * 28 = 262144,

5 = 1 - 2-7, е = 2-14.

Тогда по теореме 1 с вероятностью

Р = 1 - 10^-45

случайный щичный (n, k, d) код С имеет размерность к = 340 и расстояние как минимум 5n. Это дает процедуру идентификации с

М = 2³⁴⁰⁰

сообщениями, с вероятностью ложного приема

Л2 = 1/128 = 0.0078

и со скоростью идентификации

Ri = 0.419.

Скорость идентификации составляет только 42% от пропускной способности С = 1 из-за относительно небольших значений параметров. Зато вычисления в поле F210 не представляют большого труда. Но даже при такой скорости Ri для идентификации сообщения по каналу передается слово w длины лишь n_w = 28 бит, в то время как для передачи сообщения потребовалось бы передать 3400 бит. Платой за этот выигрыш является ненулевая вероятность ложного приема \2- Как указывалось, эта вероятность может быть уменьшена до Л2, если передавать п_шI = 281 бит [8]. Так, при I = 2 придется передать 56 бит, но вероятность ложного приема уменьшится до 0.00006.

4.    Использование генератора псевдослучайных чисел (PRNG)

При прямом использовании случайного кода недостатком является необходимость хранения порождающей матрицы как кодером, так и декодером. Избежать этого недостатка можно, если каждый раз при передаче вычислять столбец порождающей матрицы с помощью генератора псевдослучайных чисел (PRNG).

PRNG представляет собой конечный автомат, имеющий ц g-ичных элементов памяти. При заданном начальном состоянии (seed) ст Е F^q генератор порождает последовательность s = rand„(CT) требуемой длины n элементов поля. Период порожденной последовательности не может превзойти qC Мы приходим к следующей процедуре (q,k, I, p)-PRNG-идентификации.

4.1.  (q, к, I, д)-РН!\С-идентификация

Передача. Для передачи сообщения п мы выбираем случайное начальное состояние ст, генерируем с помощью PRNG один за другим I случайных вектор-столбцов g⁽¹⁾,g⁽²⁾,..., g^W Е Fy длины к, которые формируют матрицу

G(ct) = (g⁽¹⁾,g⁽²⁾,...,g^(l)).

Матрица G(ct) может рассматриваться как подматрица, состоящая из I столбцов порождающей матрицы (10) случайного кода.

Вычислим вектор т Е F^, состоящий из I признаков т/ = п/g/ сообщения п

По каналу передается идентификационное слово w = (а, т)

длины ц +1 q-ичных символов, полученное конкатенацией случайного состояния PRNG а л вектора т. состоящего из I признаков.

Декодирование. Декодер принимает слово w, переданное по бесшумному каналу, и должен решить, передавалось ли ожидаемое им сообщение и'. Декодер вычисляет матрицу G(a) (12), используя PRNG с начальным состоянием а, принятым по каналу. Затем вычисляется вектор признаков ожидаемого сообщения:

т' = u'G (а).

Если т ‘ = т, декодер принимает сообщение как ожидаемое. При и! = и декодер обязательно примет сообщение, следовательно, Аг = 0. Если же т ‘ = т, декодер отвергает сообщение. Ложный прием происходит, когда и' = и, но т' = т. Обозначим через Р2Д, и') вероятность ложного приема для пары сообщений и, и'. Мы хотим выполнения условия Р^(и, и') 6 А2 для всех пар и = и'.

Оптимальность метода зависит от параметров PRNG. Основным вопросом является следующий: какова должна быть память ц, чтобы генерировать последовательности длины Ik со свойствами, близкими к случайным?

Скорости (q, k, I, ц)-PRNG-идeнтификaции составляет

Pi =

log log \U\ ⁿW

log k + log log q (ц + I) log q

Вероятности А2 ложного принятия сообщения. Будем предполагать, что выполнено следующее условие.

Условие 1. PRNG порождает последовательность s = rand„(a) достаточной длины п независимых равномерно распределенных случайных величин s^ G F^.

Теорема 3. Пусти декодер, ожидающий сообщение и', принял идентификационное слово w = (а, т). соответствующее сообщению и. При выполнении условия 1 для любых и = и' вероятности ложного приема Р₂(и, и' ) = q^-1, т.е.

А2 = q-                                   (16)

Доказательство. Ложное принятие сообщения и вместо ожидаемого сообщения и' = и происходит тогда и только тогда, когда признаки этих сообщений совпадают, т.е. когда выполняется равенство

^G(a) = uG(a), что эквивалентно равенству vG(a) = 0,                                       (17)

где г = и' — и = 0, v G F^. По условию 1, матрица G(a) состоит из элементов поля F^, выбранных независимо и равномерно. Равенство (17) выполняется тогда и только тогда, когда каждый столбец д(г) матрицы G(a) удовлетворяет ид^ =0 г = 1,...,1,                              (18)

что происходит с вероятностью q .

4.2.    Требования к генератору PRNG

Одним из стандартных инструментов для построения псевдослучайных последовательностей являются регистры сдвига с линейной обратной связью (LFSR). LFSR легко реализуются, быстро работают и легко анализируются. В этом разделе мы исследуем возможность использования LFSR в качестве PRNG для идентификации.

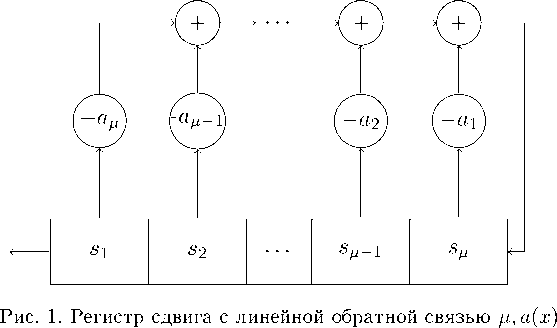
Регистр сдвига с линейной обратной связью (LFSR) показан на рис. 1. Регистр состоит из ц ячеек памяти, хранящих элементы поля F, г де ц называется длиной регистра. Начальное состояние регистра обозначим через

О = (S1,S2, ... ,8_Ц).

На г-м такте, г = 1, 2,..., с помощью обратной связи вычисляется новый элемент s^»:

Д+г

И

= ^— J2 - ^+И-3

3=1

порождаемой последовательности, содержимое регистра сдвигается налево, порождая на выходе элемент 5ц и в освободившуюся последнюю ячейку регистра записывается новый элемент б^+г- Пол ином а(х) = 1 + -1Х + а₂ х² + • • • + -цХ^И, ад = 1, над полем F называется полиномом обратной связи. LFSR длины ц с полиномом обратной связи а(х) обозначается через ц, а(х).

Теорема 4. Для выполнения оценки (16) для (q, k, I, ц)РРД G-идентификации необходимо. чтобы длина ц регистра с линейной обратной связью LFSR была как минимум k. т.е. ц > k.

Доказательство. Предположим обратное, т.е. что ц < k. Для любой последовательности s, сгенерированной с помощью LFSR ц, а(х) с произвольным начальным состоянием ст, и для любого г > ц + 1 выполняется равенство

И

Е -3 s_z-3 =0. (21) 3=0

Аналогично доказательству теоремы 3 обозначим разность двух сообщений вектором v = и — и' = 0 длины k. Поскольку сообщения могут быть любыми, вектор v = 0 может быть выбран произвольно. Вектор v построим так: возьмем вектор

^(ац, ^аи-1, . . . , ^а1, 1)

длины ц + 1 6 к и, если нужно, дополним его нулями слева до длины к. Поскольку столбцы матрицы G в (12) являются сегментами последоватености s, используя (21), получим, что выполнены условия (18) и (17) ложного приема сообщения. Поскольку для выбранной пары сообщений п, п‘ ложный прием происходит для любого выбора ст, вероятность ложного приема А2 = 1 и (16) не выполняется.

Теорема 4 показывает, что использовать LFSR в качестве PRNG в рассмотренной схеме нецелесообразно. Действительно, длина LFSR должна быть как минимум к, но тогда придется передавать идентификационное слово (14) длины более к символов поля. Это не имеет смысла, поскольку передача всего сообшения по бесшумному каналу требует пере дать лишь к символов поля.

Указанная ситуация возникла из-за того, что и псевдослучайный генератор (20) и процедура. вычисления признака. (13) являются линейными. Выйти из затруднения можно использованием нелинейного псевдослучайного генератора, или нелинейной функции вычисления признака. Хотя LFSR не может быть непосредственно использован как PRNG, известно, что комбинирование нескольких LFSR-генераторов дает возможность строить нелинейные PRNG. Вопрос о выборе PRNG и параметрах PRNG-идентификации остается открытым для дальнейших исследований.

5.    Заключение

В теории кодирования известно, что линейные случайные коды с большой вероятностью являются «хорошими», то есть достигают границы Варшамова-Гилберта. Однако на практике для передачи сообщений случайные коды не применяются. Причина, в том, что для них неизвестна, процедура, эффективного декодирования. Спецификой задачи идентификации, основанной на. кодах, является то, что декодировать коды не требуется!

Это позволило нам предложить процедуру идентификации, основанную на. случайных линейных кодах. Процедура, является оптимальной, т.е. асмптотически при росте параметров позволяет достичь идентификационной пропускной способности канала. Приведенный пример показывает, что предложенная процедура, с конечными значениями параметров кода, может быть интересной для практических применений.

Кроме того показано, что эту процедуру можно упростить применяя генераторы псевдослучайных последовательностей, однако непосредственно использовать для этого регистр сдвига с линейной обратной связью (LFSR) нельзя. Нужен или нелинейный генератор, возможно полученный комбинированием нескольких LFSR, или скалярное произведение, используемое для вычисления признака, должно быть заменено на. нелинейную функцию.

Работа, оставляет открытыми ряд вопросов, главный из которых - выбор нелинейного генератора, с небольшой памятью и большой линейной сложностью. Это может послужить темой для дальнейших исследований.

Работа, выполнена, при поддержке Федерального министерства, образования и научных исследований Германии (BMBF), Grant 16KIS1005.