Идентификация параметров гидравлического сопротивления модели гидравлической сети

Введение. В научной и отраслевой литературе предлагаются различные подходы к построению моделей гидравлических сетей [1; 2]. Многочисленные работы, такие как [3], посвящены методологии построения динамических моделей процессов, происходящих в гидравлических сетях. Зачастую, речь идет о моделях, основанных на привлечении законов гидродинамики, выраженных в системах уравнений в частных производных для описания распределенных систем. Подход, который используется в таких работах, требует исчерпывающей информации о физических характеристиках перекачиваемой жидкости, характере ее течения, внутреннем профиле и геометрической конфигурации трубопровода, исчерпывающей информации о функционировании насосных агрегатов. Во множестве случаев такие модели сложны в вычислительном плане, требуют учета неизвестных, часто неизмеримых или непредсказуемо меняющихся во времени и в пространстве параметров. Известны также исследования в области построения имитационных моделей процессов в трубопроводах, в которых недостаток априорных сведений преодолевается самим способом построения моделей совместно с упрощением их структуры [4].

Функционирование современных трубопроводных систем сопровождается сбором данных о технологических параметрах, таких как массовый или объемный расход, дифференциальный напор, давление. Измерение параметров требуется для функционирования средств автоматизированного управления, в частности, диспетчерского контроля. При этом надежность и эффективность управления технологическим процессом трубопроводного транспорта нефти и газа напрямую зависит от качества и точности математических моделей технологических процессов, являющихся основной и неотъемлемой частью автоматизированных систем управления. Построение математических моделей рассматривается в терминах теории идентификации [5].

Один из основных подходов к построению моделей трубопроводных систем основывается на представлении структуры гидравлической системы в виде плоского связного орграфа с определенным набором вершин (узлов), ребер (ветвей) и граней (контуров) и позволяет решать задачи стационарного потокорас-пределения. Модель в рамках такого подхода представляет собой большую систему нелинейных уравнений, составленную в соответствии с законами Кирхгофа для трубопроводной сети [6; 7]:

cn xi + -+cinxn = qi, ck-1,1 xi + - + ck-1, nxn = qk-1, ck 1 S1 |x11₽1 -1 X1 + - + cknsn |xn |Pn -1 xn = h1,

c n1 ^S 1 | x 1 |^{P1 - 1 X} 1 + - + c nn s n | x n |^P n ^{- 1} x n = h n - k + 1 , где n – количество участков в графе сети; k – количество узлов; X j , j = 1, 2, - , n , - расход по j -й трубе; q i , i = 1, 2, - , k - 1, - приток в узле; S j , j = 1, 2, - , n , -гидравлическое сопротивление соответствующей трубы; h i , i = 1, 2, - , n - k + 1, - сумма действующих напоров с учетом знака по всем дугам i -го контура; в - коэффициент в законе зависимости величины падения напора от значения расхода; c ij = { - 1,0, + 1 } определяется по первому или второму закону Кирхгофа. Для второго закона Кирхгофа и для нелинейных уравнений c j = { - 1, + 1 } (в зависимости от направления обхода), если j -й участок входит в цикл, соответствующий i -му нелинейному уравнению, либо c j = 0 . Система уравнений (1) имеет единственное решение [8].

Построение модели (1) связано с решением двух задач:

• 1)    нахождение неизвестных значений расходов сети при заданных значениях активных напоров (прямая задача);

• 2)    настройка параметров гидравлического сопротивления – идентификация параметров гидравлического сопротивления (обратная задача).

По модели (1) на предприятиях, эксплуатирующих трубопроводные сети, производится расчет некоторого множества возможных технологических режимов работы сети, которые с той или иной вероятностью могут быть реализованы. По результатам моделирования вычисляются значения расходов каждой из труб и значения активных напоров сети, необходимых для обеспечения заданного отбора в узлах. Такой подход позволяет производить управление режимами работы сети.

Основным алгоритмом решения системы уравнений (1), применяемым на практике, является модифицированный метод последовательных приближений [9]. Данный алгоритм является модификацией метода Ньютона с более высоким показателем скорости сходимости при достаточно произвольном выборе начального приближения.

При этом точность решения прямой задачи в значительной степени зависит от точности известных значений параметров гидравлического сопротивления. Если значения параметров известны неточно, то решение может быть далеким от действительности. В настоящий момент для решения задачи идентификации параметров гидравлического сопротивления применяется метод наименьших квадратов, либо задача сводится к эквивалентной задаче линейного программирования [10]. Применение метода наименьших квадратов к системе (1) для идентификации параметров гидравлического сопротивления приводит к переопределенной системе нелинейных уравнений. Решение такой системы уравнений относится к классу некорректных задач, так как полученная система может и не иметь решений.

На практике установлено, что такой подход позволяет производить настройку параметров гидравлического сопротивления только в случае небольших размерностей (для сетей с количеством участков не более 200). Для сетей больших размерностей не всегда удается получить решение с приемлемой точностью для всех коэффициентов гидравлического сопротивления [11]. Кроме того, на практике в каналах связи и регистрирующей аппаратуре присутствуют случайные помехи аддитивного и мультипликативного типа. Применение метода наименьших квадратов, в случае наличия помех и выбросов в выборках измерений, приводит к снижению качества идентификации, что свойственно данному классу методов [12].

В связи с этим разработка алгоритмов идентификации параметров гидравлического сопротивления, обеспечивающих необходимою точность и помехоустойчивость, является актуальной задачей. В настоящей статье в качестве подхода к идентификации параметров гидравлического сопротивления предлагается использовать модификацию алгоритма Кифера-Вольфовица [13] в приложении к идентификации многосвязных систем [14; 15]. Идентификация параметров производится с одновременной оценкой решения системы уравнений (1).

Алгоритм идентификации параметров гидравлического сопротивления с одновременной оценкой решения. В качестве алгоритма идентификации предлагается использовать алгоритм, основанный на алгоритме Кифера-Вольфовица [13]. В качестве метода решения системы уравнений в алгоритме используется метод генерации решений [14].

Введем следующие обозначения: у - коэффициент, удовлетворяющий условиям Роббинса-Монро [16]; l - размерность системы; f i , i = 1, l - i -е уравнение сис

3. Оценка решения системы уравнений на m -м шаге:

x j ( m ) =

ml

Z x j [ t ] П Ф t = 1            j = 1

0 -S j [ t ] c j

ml

zn Ф

t = 1 j = 1

' 0-s/t]" c

, j = 1, l ,

темы; V = { h[t ], x [ t ] } , t = 1, N , - обучающая выборка.

Алгоритм выглядит следующим образом:

1. Оценка параметров системы на m -м шаге:

S j [ m ] = S j [ m - 1] - Y j ) [ m ] ■ f ( h ⁽ i ) [ m ], x ⁽ i ) [ m ], s ⁽ j ) [ m - 1] ) ,

j = 1, l ,

2. Вычисление невязок системы на m -м шаге:

S j [ m ] = f j ( h ^{( j )}[ m ], x ^{( j )}[ m ], s ^{( j )}[ m ] ) , j = 1, l .            (3)

где ядерная функция Ф(^) и параметры размытости c j , j = 1, 2, .., l , удовлетворяют условиям сходимости [12].

4. Проверка критерия остановки: если

V(sj(m)- sj(m-1))2 <51

или

Z V⁽ x j ⁽ m ) - x j⁽ m - ^{1)) 2} <^б 2 , j = 1

то алгоритм останавливается, иначе m = m + 1 и переход на первый пункт. Здесь 5 1 и 5 ₂ - некоторые заданные положительные значения.

Исходная трубопроводная сеть, генерация обучающей выборки. Рассмотрим применение предложенного подхода на примере трехкольцевой трубопроводной сети, изображенной на рис. 1 [17].

На рис. 1 стрелки в контурах отвечают выбранным направлениям обхода. В цепи имеется одна активная ветвь с действующим напором H . Жирными линями обозначены дуги дерева, тонкими - хорды. Номера дуг заданы таким образом, что первые номера получили дуги дерева, а оставшиеся - хорды.

Число дуг n = 10, узлов к = 8, размерность системы l = 10. Все трубы, кроме шестой и седьмой, стальные и удовлетворяют квадратичному закону гидравлического сопротивления, шестая и седьмая - пластмассовые, для них в = 1,774. Величина напора h = 8,3.

Система уравнений для такой сети, составленная в соответствии законами Кирхгофа для трубопроводной сети и моделью распределения потоков в виде h = sx ^e (параметризованная система), примет следующий вид:

- x 1 + x 8 = - 89, x 1 + x ₂ - x ₄ = 16,5, - x ₂ + x ₅ = 19,2, - x 5 + x 9 = 23,1, - x 3 + x 4 + x 7 - x 9 = 0, ^- x ₇ + x ₁₀ = ^17,4, x 6 - x 10 = 12,8,                       (5)

0,00147| x j x 1 + 0,00431| x ₃| x ₃ +

+ 0,00174| x ₄|^0,774 x ₄ + 0,00174| x ₈|^0,774 x ₈ = h ,

0,0023 1 x ₂ 1 x ₂ + 0,00174 1 x ₄ 1^0,774 x ₄ +

+ 0,00522| x ₅ 1 x ₅ + 0,00174| x ₉| x ₉ = 0, 0,00431 1 x ₃| x ₃ + 0,00514 1 x ₆| x ₆ +

+ 0,00514 1 x ₇| x ₇ + 0,00522 1 x ₁₀| x ₁₀ = 0.

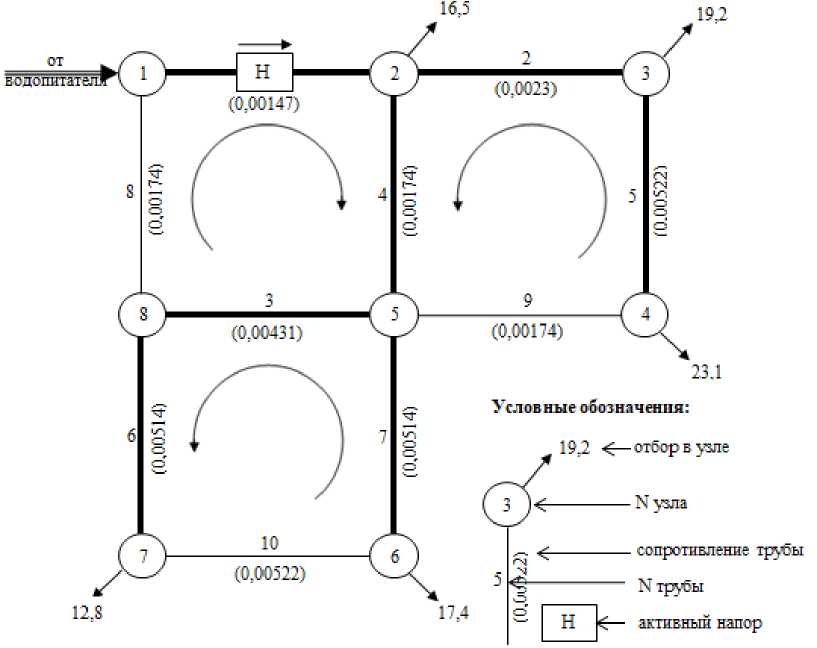
Рис. 1. Схема трехкольцевой трубопроводной сети

Fig. 1. Layout of three-loop pipeline network

В качестве входных воздействий (активного напора h ) определим

h[t] = h • (1 + 2 • p • (ц[t] - q)), t = 1, N, где p – разброс выборочных значений от начального состояния; ц[t], t = 1, N, - последовательность случайных чисел, равномерно распределенных на отрезке [0,1]; q - параметр сдвига.

Преобразуем выборочные значения по формуле

—w-                                                                                                               1

h[t] = h[t] • (1 + 2 • 5 • (r[t] - q)), t = 1, N, где 5 - шум на объекте; r[t], t = 1,N, - последовательность случайных чисел, равномерно распределенных на отрезке [0,1] .

Генерацию выборочных значений выхода (расходов) x [ t ] = ( x 1[ t ], ..., x l [ t ] ) при заданном входе h [ t ] осуществим в ходе решения системы (5) методом Ньютона.

Таким образом, в качестве исходной обучающей выборки вектора состояний трубопроводной сети примем выборку { h [ t ], x [ t ] } , t = 1, N .

Результаты идентификации. Численное исследование алгоритма проведем при следующих параметрах:

• -    начальное значение активного напора h = 8,3;

• -    разброс выборки от начального состояния p = = 25 %;

• -    уровень шума 5 е { 5 %, 10 %, 25 % } ;

• -    параметр сдвига q = 0,5;

• -    объем обучающих выборок N е { 25, 50, 100 } ;

• -    коэффициент y = V m , где m — шаг.

Численное исследование алгоритма идентификации с одновременной оценкой параметров для разного уровня шума в зависимости от такта идентификации m приведено ниже. Так как графики оценки параметров схожи, то приведены графики оценки параметра лишь для одного (первого) параметра гидравлического сопротивления s ₁ (рис. 2–4). На графиках s ₁^* обозначает истинное значение параметра гидравлического сопротивления s ₁.

В соответствии с рис. 2–4 можно сделать вывод, что найденные оценки параметра s 1 стремятся к своим истинным значениям и, начиная с пятого шага, практически остаются на одном уровне. Наблюдается достаточно высокая помехоустойчивость алгоритма оценки параметров.

В качестве критерия качества оценки решения использовался следующий критерий (евклидовая норма отклонения найденного решения от истинного):

l ₂

W = Е^ I ^х/ ^- x r | , j = 1

где x_j – оценка решения; x_r – истинное решение.

Результаты оценки решения представлены в таблице, где приведена ошибка идентификации W для разного объема выборки N и уровня шума S в каналах измерения.

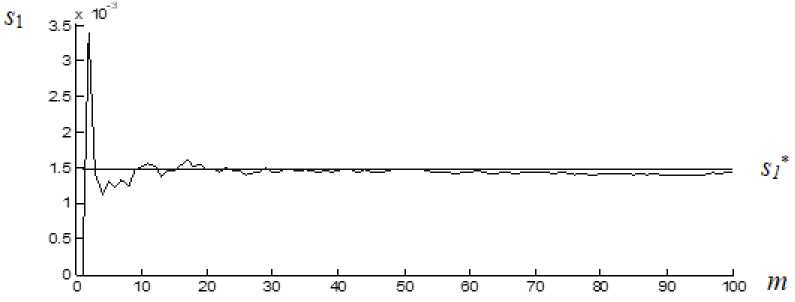
Рис. 2. Оценка параметра гидравлического сопротивления s ₁ при S = 5 %

Fig. 2. Hydraulic resistance estimate s 1 vs. iteration for noise amplitude S = 5 %

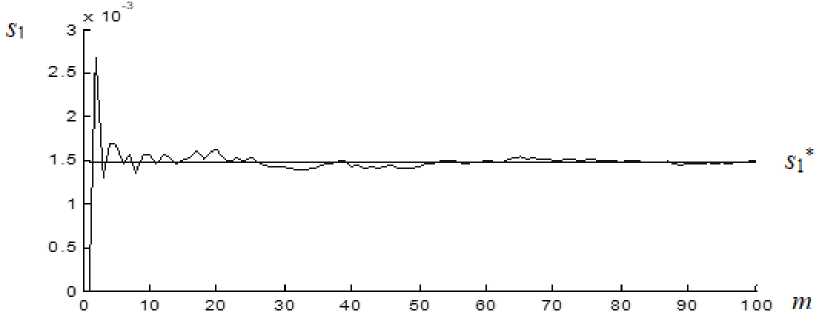
Рис. 3. Оценка параметра гидравлического сопротивления s ₁ при S = 10 %

Fig. 3. Hydraulic resistance estimate s ₁ vs. iteration for noise amplitude S = 10 %

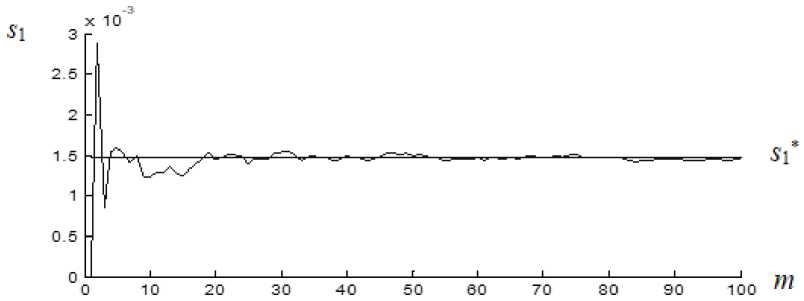
Рис. 4. Оценка параметра гидравлического сопротивления s ₁ при S = 25 %

Fig. 4. Hydraulic resistance estimate s 1 vs. iteration for noise amplitude S = 25 %

Результаты расчета критерия качества оценки решения

S = 5 %
N	25	50	100
W	0,09636	0,07330	0,05282
S = 10 %
N	25	50	100
W	0,17085	0,13315	0,08306
S = 25 %
N	25	50	100
W	0,34195	0,29205	0,22395

С увеличением объема обучающей выборки точность оценки решения увеличивается, что свидетельствует о сходимости алгоритма. Наличие помехи в каналах измерения негативно сказывается на работе соответствующих оценок.

В целом по ряду экспериментов была установлена достаточно высокая точность при относительно небольших объемах обучающих выборок и устойчивость к шуму, вплоть до достаточно больших значений помехи.

Заключение. Рассмотрен подход к идентификации параметров гидравлического сопротивления с одновременной оценкой решения системы уравнений для гидравлической сети. Применение предложенного подхода позволит избежать трудностей, связанных с применением метода наименьших квадратов: пере-определенность системы уравнений, чувствительность к выбросам. Рассмотренная процедура идентификации параметров гидравлического сопротивления обеспечивает высокую помехоустойчивость, приемлемую скорость и точность идентификации.

Планируется, что дальнейшие исследования будут включать анализ данных и построение модели реальной функционирующей гидравлической сети.