Идентификация процесса теплообмена котлового оборудования на основе возмущенных данных
Автор: Дилигенская А.Н., Осянина Л.В.
Журнал: Вестник Южно-Уральского государственного университета. Серия: Энергетика @vestnik-susu-power
Рубрика: Теплотехника
Статья в выпуске: 4 т.24, 2024 года.
Бесплатный доступ
Рассматривается процесс нестационарной теплопроводности, ставится задача нахождения коэффициентов конвективного теплообмена между рабочей средой и внутренней поверхностью стенки барабана котла, а также между наружной теплоизолированной поверхностью и окружающей средой по результатам измерения температуры его внешней поверхности, полученным с учетом погрешностей измерения. Контроль ненаблюдаемых коэффициентов теплопроводности направлен на предотвращение деформации металла барабана при его нагреве и обеспечение интенсификации процесса паро- и водоподготовки. Моделирование температурных распределений производится на базе структурной теории распределенных систем. Формулируется обратная задача теплопроводности, и проблема сводится к задаче поиска оптимального управления ансамблем траекторий с интервальными неопределенностями, когда считается известной информация о границах диапазона возможного распределения температуры. Параметризация искомых коэффициентов в классе постоянных функций и учет альтернансных свойств оптимальных температурных распределений приводят к задаче параметрической оптимизации, сформулированной относительно всей совокупности температурных реализаций на расширенном множестве аргументов. Решение задачи обеспечивает гарантированное качество идентификации для наиболее неблагоприятной траектории. Результаты решения задачи на основе зашумленных экспериментальных данных, полученных на котловом оборудовании газотурбинной установки, демонстрируют работоспособность метода.
Процесс теплопроводности, барабан котла, коэффициент конвективной теплоотдачи, идентификация, обратная задача теплопроводности, погрешности измерения, ансамбль траекторий, параметрическая оптимизация
Короткий адрес: https://sciup.org/147247637
IDR: 147247637 | УДК: 536.2, | DOI: 10.14529/power240410
Текст научной статьи Идентификация процесса теплообмена котлового оборудования на основе возмущенных данных
Решение проблемы интенсификации теплообменных процессов невозможно без их точного адекватного математического описания с использованием современных научных подходов. В области прикладной теплотехники в условиях действия большого количества разнообразных возмущающих факторов для получения адекватной математической модели производится уточнение значений её параметров на основе экспериментально полученных данных. Одной из таких задач является задача определения коэффициента конвективного теплообмена между рабочей средой и внутренней поверхностью стенки барабана котла по измеряемым значениям температуры на его внешней поверхности, которая возникает в процессе подготовки пароводяной смеси при функционировании газотурбинных установок.
Обзор научных исследований
Одним из наиболее эффективных средств восстановления ненаблюдаемых характеристик и параметров по косвенным признакам их проявления является теория обратных задач теплопроводности (ОЗТ). Основы теории ОЗТ составляют такие подходы, как итерационная регуляризация [1], параметрическая и функциональная идентификация, автоматизированный метод подбора [2], разностные методы и методы регуляризации [3, 4], метод сопряженных градиентов [5] и другие. На их основе решены актуальные задачи определения теплофизических характеристик и коэффициентов теплообмена [6–10] по доступным для измерения результатам экспериментов. В настоящее время для решения прикладных обратных задач инженерной теплофизики [10–12] применяется широкий круг методов, основанных на различных подходах теории некорректных задач, теплопроводности, математической физики, оптимального управления, вычислительной математики и других [6–13].
Актуальность
Востребованность задачи [6–12] обусловлена, во-первых, необходимостью контроля параметров теплообмена для обеспечения поддержания бездефектного состояния котлового оборудования, а также для его надежного функционирования и
повышения КПД, а во-вторых, тем, что в условиях сложного неоднозначного многопараметрического характера зависимости идентифицируемых характеристик от совокупности теплофизических, геометрических показателей и режимных параметров ОЗТ являются одним из наиболее эффективных и доступных способов их определения. При этом реальные экспериментальные данные подвержены действию возмущающих факторов, в первую очередь, погрешностей измерений, и при использовании статистических методов обработки данных, обладающих сглаживающим эффектом, необходимо не потерять существенные особенности теплообменных процессов.
Научная новизна
В статье предложен подход к определению коэффициентов конвективного теплообмена на основе реальных экспериментальных данных, основанный на методах оптимального управления системами с распределенными параметрами [14, 15] с учетом интервальных неопределенностей возмущений. Новизна предложенного подхода состоит в том, что он реализует стратегию гарантированного результата для всех возможных вариантов действия возмущающих факторов.
Постановка задачи
Рассматриваются тепловые процессы на газотурбинной установке, в которых для подготовки пароводяной смеси используется котёл-утилизатор барабанного типа с естественной циркуляцией в испарительных контурах высокого давления.
Барабан котла относится к объектам с распределенными параметрами, учитывающими изменение функции состояния – температуры T ( x , t ) – не только во времени, но и в пределах пространственной области, занимаемой объектом. Процесс теплопередачи в стенке барабана котла описывается уравнением математической физики параболического типа с соответствующими краевыми условиями. В первом приближении, принимая изменение теплового состояния вдоль стенки барабана незначительным по сравнению с температурной неравномерностью по толщине стенки, процесс рассматривается на примере одномерного уравнения.
За базовую модель принята линейная модель с конвективным теплообменом на каждой из поверхностей стенки барабана, учитывающая также тепловые потери на внешней теплоизолированной поверхности, присутствующие в реальных производственных условиях:
д т ( x , t ) д 2 t ( x , t ) n n n
—= a ---- . , 0 < x < R , t > 0;
д t д x 2
T ( x ,0) = T o ( x );
д T (0, t ) _ / \ (1)
-
^_ a i ( Т ср1 ( t ) - T (0, t) ) ;
д T ( R , 11)
-
-^“ a 2 ( T CP2 ( t ) - T ( R ’ t) ) .
Здесь R – толщина стенки барабана котла; a = λ/( c γ) – коэффициент температуропроводности материала, где λ, c, γ – коэффициент теплопроводности, удельная теплоемкость и плотность металла; α1 и α2 – усредненные величины коэффициентов теплопередачи на соответствующих границах; T ср1 ( t ) и T ср2 ( t ) – температура окружающей среды на поверхностях стенки барабана.
Для решения краевой задачи (1) была использована структурная теория систем с распределенными параметрами [16–18]. На её основе структурное представление объекта (1) состоит из суммы двух составляющих [18, 19], имитирующих процесс конвективного теплообмена от внешних воздействий T ср1 ( t ) и T ср2 ( t ) . Каждая из составляющих может быть представлена в виде суммы бесконечного числа n = 1, 2, … апериодических звеньев первого порядка с передаточными функциями W n ( s ) = k n ( x , ^ )/( т n s + 1) с по-
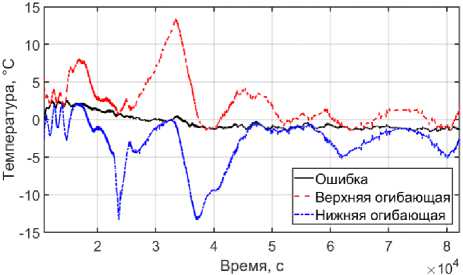
R2 1 Пnx Пn стоянными времени тn =——- и коэффициентами передачи kn (x, у = 2тn cosl---I cos II, завися- an2n2 I R J I R J щими от координат точки ξ приложения внешнего воздействия и точки x контроля температуры. При имитационном моделировании объекта обычно ограничиваются таким числом звеньев, при котором (T(N+1)(x, t) _ т(N)(x, t))It(N)(x, t) Методология исследования Температура окружающей среды на теплоизолированной внешней поверхности принята Тср1 (t) = 20 °С = const. Экспериментальные данные о температуре воды на входе в испаритель высокого давления образуют массив значений внешнего воздействия Tср2(t) . В качестве дополнительной входной информации используется массив экспериментальных значений температуры металла барабана высокого давления Т = [Т*(t)], Т*(t) = Т*(x*, t), i = 1,6, полученных на интервале идентификации в шести точках термометрирования x*, i = 1,6 на наружной поверхности стенки барабана. Данные отобраны в режиме холодного пуска котла на интервале общей длительности 82 173 c, на котором наблюдаются переходные динамические и установившиеся статические режимы. Задача для каждой i-й экспериментальной температурной кривой Т *( x*, t), i = 1,6 сформулирована в экстремальной постановке. По зашумленной температурной реализации Ti*(t) , полученной в точке термо-метрирования xi* на интервале идентификации, требуется восстановить неизвестные значения коэффициентов конвективного теплообмена а1 и а2, минимизирующие температурную невязку между экспериментальной кривой и решением задачи TM (x*, t, а1, а2), соответствующим искомым значениям а1 и а2. При отсутствии случайных возмущений свою эффективность при решении ОЗТ показал метод параметрической оптимизации [20], основанный на поиске решений на компактных множествах при оценивании температурной невязки Т*(t) - TM (x*, t, а1, а2) между экспериментальным и расчетным значением в равномерной метрике. Исходная задача сводится к задаче параметрической оптимизации, и для её решения используются альтернансные свойства [14, 15] оптимальных температурных распределений, которые позволяют определить возможные варианты конфигурации температурной невязки. При действии погрешностей измерения, распределенных по случайному закону, оптимальная конфигурация Т*(t) - TM (x*, t, а1, а2) существенно изменяется, и определить точки альтернанса при составлении системы расчетных соотношений для вычисления значений вектора параметров бывает затруднительно. Статистическая обработка экспериментальных данных позволяет понизить уровень шума, но может способствовать искажению характерных особенностей динамики процесса. В такой ситуации может быть применен подход, предусматривающий параметрическую оптимизацию ансамбля траекторий с интервальными неопределенностями [21], при котором полагается, что экспериментальная температурная кривая обладает неполнотой информации, которая выражается сведениями о границах Tmin(t) и Tmax(t) диапазона возможного распределения температуры, и вместо одной возмущенной температурной кривой T*(xi*,t) рассматривается совокупность TΩ бесконечного числа k = 1, 2, … возможных реализаций Tk1 (x*,t) на множестве О допустимых вариантов, удовлетворяющих условию Tmin(t) < T1 (X*,t) < Tmax(t), k = 1,2, (2) Тогда ОЗТ формулируется по отношению к совокупности TΩ бесконечного числа температурных траекторий с полной информацией, удовлетворяющих всем возможным вариантам в условиях ограничений (2). Задача в экстремальной постановке рассматривается как задача оптимального управления Ij (a1, a2) = min k =1,2,... min, Tkn (xi,t) - TM (xi,t, a1, a2 t e[0, tf J1 ^ min , aj ,a2 e V в которой для объекта (1) необходимо найти оптимальные управляющие воздействия α1 и α2, принадлежащие заданному классу функций V, для всего ансамбля TΩ температурных реализаций, удовлетворяющих неравенству (2). Апробированный на широком спектре ОЗТ [20, 21] метод последовательной параметризации в этом случае также обеспечивает редукцию задачи (3) к задаче минимаксной оптимизации относительно ошибки | T1 (x*, t) - TM (xi, t, a1, a2)| равномерного приближения модельного решения к измеренной температуре. Отличительной особенностью здесь будет тот факт, что в условиях интервальной неопределенности задача (3) рассматривается как задача оптимального управления всей совокупностью температурных реализаций. Данный подход предусматривает задание класса решений V в виде компактного множества функций, что соответствует параметризации искомой характеристики α = α(T) с помощью вектора параметров Δ и приводит к условно-корректной постановке задачи. Для максимального использования особенностей математического моделирования бесконечномерных систем в статье была использована аналитическая линейная модель (1), в которой поиск коэффициентов теплоотдачи был реализован на множестве постоянных функций α(T) = α = const. Такое описание может быть использовано в качестве первых приближений для оценки неизвестных параметров теплообмена. В этом случае искомые функции α1 = Δ1 и α2 = Δ2 однозначно заданы обобщенным вектором параметров, содержащим два компонента Δ = (Δ1, Δ2). Температурное поле также параметризуется вектором Δ = (Δ1, Δ2), что позволяет свести исходную ОЗТ к задаче параметрической оптимизации, которая сформулирована относительно всей совокупности температурных реализаций TΩ на расширенном множестве аргументов (t, Ω) 12 (Л) = min k =1,2,... min, ITT (x*,t) - TM (xi,t, л)| t e|0, tf J1 1 ^ min. Л Найденное в соответствии с (4) оптимальное управление Δ = Δ0 гарантирует минимально возможную погрешность приближения для наиболее неблагоприятной, ограниченной условием (2) траектории T^1 (x*, t), обладающей максимальным по абсолютной величине отклонением от модельной реализации. По очевидным физическим соображениям кривые Tmin(t) и Tmax(t) локализуют весь ансамбль возможных траекторий. Тем самым для остальных возможных реализаций погрешность аппроксимации будет меньше рассчитанного в соответствии с (4) отклонения. Вынужденная потеря качества идентификации по величине функционала (4) отражает требование гарантированного результата в условиях интервальной неопределенности. Решение задачи с интервальными неопределенностями Обобщенный вектор v = (t, Ω), содержащий совокупность всех значений tϵ[0,tf] и k = 1, 2, …, соответствует всем возможным реализациям Tk1 (x*, t), и задача математического программирования (4) записывается для полной совокупности Т, (Л) = min\тк1(x**,t) -TM (x,t,Л)| ^ min. (5) v I I Л Поиск максимума абсолютного температурного отклонения осуществляется на множестве (t, Ω) возможных реализаций k = 1, 2, …, процесса и значений моментов времени t ϵ [0, tf]. Свойства оптимальных температурных распределений, аналогичные чебышевскому альтернансу, относятся ко всей полученной совокупности, и точки альтернанса v = (t, Ω) в общем случае содержат любые комбинации неопределенных факторов. Это приводит к тому, что максимумы и минимумы температурных невязок наблюдаются в разные моменты времени на разных реализациях функции состояния. Для их поиска также применен альтернансный метод [14, 15] с той особенностью, что необходимо распознавать соответствующие траектории, где достигаются максимальные и минимальные отклонения. Физические соображения приводят к тому, что максимумы и минимумы температурной невязки достигаются на предельных реализациях, ограничивающих весь ансамбль траекторий сверху (на верхней огибающей Tmax(t)) и снизу (на нижней огибающей Tmin(t)). Для численного решения задачи осуществляется переход к задаче минимизации в пространстве искомых параметров целевой функции Iз(Д) = E(F(*>t(max)^^ A°))2 ^min; (6) j, rЛ F (•) = TU x*, t . - Tm (x*, t (max),Д°) + TL( x*, trmX - Tm (trmX A°), сформированной в результате сложения квадратов алгебраической суммы температурных невязок на максимально и минимально возможных реализациях в точках t(jmax) , tr(min) их предельных отклонений. При оптимальном решении Δ = Δ0 достигается равный нулю глобальный минимум функционала (6). Экспериментальная часть и результаты идентификации Некоторые из полученных результатов идентификации коэффициентов конвективной теплоотдачи приведены на рисунке и в таблице. Время, c xiQ4 а – Расчет № 1 b – Расчет № 2 Погрешность аппроксимации температурного распределения Temperature distribution approximation error Результаты идентификации Identification results α1, Вт/(м2К) α2, Вт/(м2К) Минимаксная ошибка εT, % Расчет № 1 29,3 350,5 11,2 Расчет № 2 19,17 596,8 6,5 Экспериментальные данные, полученные на интервале идентификации, содержат участок быстрого нагрева t ϵ [0, 10 876] c и последующие участки более медленного изменения температуры и её стабилизации t ϵ [10 876, 82 173] c. Расчет № 1 был проведен на всём временном интервале t ϵ [0, 82 173] c. Результаты идентификации данного режима в классе постоянных значений приводят к существенной погрешности аппроксимации совокупности температурных реализаций на начальном участке и к смещению температурной невязки на последующем интервале, что объясняется разной динамикой процесса на отдельных интервалах: значительным ростом температуры на первом небольшом участке и её медленным изменением в дальнейшем; зависимостью от температуры коэффициента α2; действием возмущающих факторов. Расчет № 2, выполненный на интервале t ϵ [10 876, 82 173] с, не содержащем участка быстрого нагрева, показывает лучшее качество идентификации. Полученная погрешность значительно меньше, а её смещение к концу интервала стремится к нулю. При этом максимальная абсолютная температурная невязка st = Tmx(x*,t(max))-Tm(x*,t(max),A°)| = Tmn(x*,tr™0)-Tm(x*,trmXA°)| соответствует наихудшим (максимально отдаленным) реализациям процесса. Для остальных температурных траекторий погрешность будет меньше. Относительное значение невязки εT, % (см. таблицу) рассчитано по отношению к конечному моменту времени. Отличительной особенностью метода является обеспечение гарантированного качества восстановления коэффициентов теплоотдачи барабана котла в условиях действия возмущений при отсутствии процедур регуляризации решения и теплотехнического сглаживания, вносящих искажения в полученные результаты. Экспериментально полученные результаты подтверждают работоспособность предложенного подхода, точность решения соответствует инженерным требованиям. Практическая значимость предложенного метода состоит в том, что он обеспечивает нахождение устойчивых приближений к искомым значениям коэффициентов теплообмена на котловом обо- рудовании газотурбинных установок на основе экспериментальных данных в условиях отсутствия априорной информации о возмущающем воздействии. Выводы 1. На основе решения ОЗТ определены значения коэффициентов теплоотдачи. Учет погрешностей измерения существенно влияет на результаты их восстановления. Тем не менее предложенный подход обеспечивает гарантированное качество решения ОЗТ для всего ансамбля траекторий. 2. Уменьшение интервала идентификации и выделение участков разной динамики в отдельные самостоятельные задачи позволят повысить качество идентификации. На представленных экспериментальных данных ошибка идентификации уменьшилась до 6,5 % по отношению к 11,2 % при использовании временного интервала t ϵ [10 876, 82 173] с по сравнению с интервалом t ϵ [0, 82 173] c.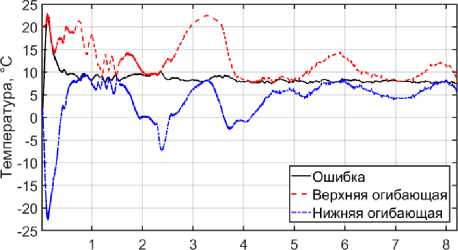
Список литературы Идентификация процесса теплообмена котлового оборудования на основе возмущенных данных
- Алифанов, О. М. Обратные задачи теплообмена / О.М. Алифанов. – М.: Машиностроение, 1988. – 280 с.
- Мацевитый, Ю. М. Обратные задачи теплопроводности / Ю.М. Мацевитый. – Киев: Наукова думка, 2002. – 405 с.
- Beck J.V., Blackwell B., St. Clair C.R. Inverse Heat Conduction. Ill-posed Problems. N.Y.: J. Wiley and Sons Publ., 1985. 308 p.
- Самарский, А. А. Численные методы решения обратных задач математической физики. Учебное пособие / А.А. Самарский, П. Н. Вабищевич. – 3-е изд. – М.: ЛКИ, 2009. – 480 с.
- Ozisik M. N., Orlande H. R. B. Inverse Heat Transfer: Fundamentals and Applications. Routledge, 2018.
- Зверев, В.Г. Определение коэффициента теплоотдачи и температуры газового потока по измерениям температуры материала / В. Г. Зверев, А. А. Светашков А. В. Теплоухов // Теплофизика высоких температур. – 2021. – Т. 59, №1. – С. 140–147
- Albu A., Zubov V. Identification of the thermal conductivity coefficient in two dimension case. Optimization Letters, 2019, vol. 13, no. 8, pp. 1727–1743. doi: 10.1007/s11590-018-1304-4.
- Borukhov V. T., Tsurko V.A., Zayats G.M. The functional identification approach for numerical reconstruction of the temperature-dependent thermal-conductivity coefficient. International journal of heat and mass transfer, 2009, vol. 52, pp. 232–238. doi: 10.1016/j.ijheatmasstransfer.2008.01.043.
- Borukhov V. T., Kostyukova O. I. Reconstruction of heat transfer coefficients using the approach of stage-by-stage suboptimal optimization and Huber–Tikhonov filtering of input data. Automatic Control and Computer Sciences, 2013, vol. 47, no. 6, pp. 289–299. doi: 10.3103/S0146411613060047.
- Lu T., Han W.W., Jiang P.X., Zhu Y.H., Wu J., Liu C.L. A two-dimensional inverse heat conduction problem for simultaneous estimation of heat convection coefficient, fluid temperature and wall temperature on the inner wall of a pipeline. Applied Thermal Engineering, 2015, no. 81, pp. 161-168. doi: 10.1016/j.pnucene.2015.01.018.
- Mohebbi F., Evans B., Rabczuk T. Solving direct and inverse heat conduction problems in functionally graded materials using an accurate and robust numerical method. International Journal of Thermal Sciences, 2021, vol. 159. doi: 10.1016/j.ijthermalsci.2020.106629
- Shen L., Jiang Z., Gui W., Yang C., Wang Y., Sun B. Modelling of Inner Surface Temperature Field of Blast Furnace Wall Based on Inverse Heat Conduction Problems. IFAC-PapersOnLine, 2019, vol. 52, no. 14, pp. 78 – 83. doi:10.1016/j.ifacol.2019.09.167.
- Alifanov O.M. Inverse Problems in Identification and Modeling of Thermal Processes: Russian Contributions. International Journal of Numerical Methods for Heat & Fluid Flow, 2017, vol. 27, no. 3, pp. 711–728. doi: 10.1108/HFF-03-2016-0099.
- Рапопорт, Э. Я. Точный метод в задачах оптимизации нестационарных процессов теплопроводности / Э.Я. Рапопорт // Известия АН СССР. Энергетика и транспорт. – 1978. – № 4. – С. 137–145
- Рапопорт, Э. Я. Алгоритмически точный метод параметрической оптимизации в краевых задачах оптимального управления системами с распределенными параметрами / Э.Я. Рапопорт, Ю.Э. Плешивцева // Автометрия. – 2009. – Т. 45, № 5. – С. 103–112
- Рапопорт, Э.Я. Структурное моделирование объектов и систем управления с распределенными параметрами / Э.Я. Рапопорт – М.: Высшая школа, 2003. – 299 с.
- Бутковский, А.Г. Структурная теория распределенных систем / А.Г. Бутковский. – М.: Наука, 1977. – 320 с.
- Бутковский, А.Г. Характеристики систем с распределенными параметрами / А.Г. Бутковский. – М.: Наука, 1979. – 224 с.
- Данилушкин И.А. Численно-аналитическая модель температуры металла барабана парового котла / И.А. Данилушкин, С.А. Колпащиков, И.С. Левин // Вестник Самарского государственного технического университета. Серия «Технические науки». – 2023. – Т. 31, № 1. – С. 21–33
- Diligenskaya A. N., Rapoport E. Y. Method of minimax optimization in the coefficient inverse heat-conduction problem. Journal of Engineering Physics and Thermophysics, 2016, vol. 89, no. 4, pp. 1008–1013. doi: 10.1007/s10891-016-1462-0.
- Дилигенская, А. Н. Параметрическая оптимизация в обратных задачах теплопроводности в условиях интервальной неопределенности возмущений / А.Н. Дилигенская // Проблемы управления и моделирования в сложных системах: труды XX Международной конференции. – Самара: Общество с ограниченной ответственностью "Офорт", 2018. – С. 112–118.


