Идентификация трещиноподобного дефекта и исследование концентрации напряжений в полосе с покрытием
Автор: Соболь Б.В., Соловьев А.Н., Рашидова Е.В., Васильев П.В.
Статья в выпуске: 4, 2019 года.
Бесплатный доступ
Первый раздел статьи посвящен локации дефектов в полосе с покрытием и идентификации их геометрических параметров. С применением методов конечноэлементного моделирования, ультразвукового неразрушающего контроля и технологий машинного обучения (искусственных нейронных сетей) решена обратная задача механики. Построена конечно-элементная модель распространения ультразвуковой волны в полосе с покрытием и внутренним дефектом. По сравнению с предыдущими работами в модели применены слои PML (Perfectly Matched Layer), или идеально согласованные слои, которые подавляют множественные отражения зондирующего ультразвукового импульса внутри полосы и предотвращают зашумление сигнала. На основе проведенных численных расчетов конечно-элементной модели построен набор данных, содержащий геометрические параметры дефекта и соответствующую им амплитудно-временную характеристику ультразвукового сигнала. Разработана архитектура искусственной нейронной сети прямого распространения. Проведено обучение нейронной сети на основе предварительно обработанных данных. В результате на основе ультразвуковых данных, полученных с внешней поверхности полосы, возможно восстановить значения таких параметров дефекта, как глубина залегания, длина и толщина. Во втором разделе статьи описана аналитико-численная технология исследования коэффициента интенсивности напряжений (КИН) в вершине трещины на примере задачи о продольной внутренней трещине конечной длины, расположенной в упругой полосе, усиленной тонким гибким покрытием. Решение этой задачи основано на методе интегральных преобразований, который позволил свести ее к сингулярному интегральному уравнению I рода с ядром Коши, которое решается методом коллокаций в виде разложения по полиномам Чебышева с множителем, явно учитывающим особенность в окрестности вершин трещины. Последнее позволяет непосредственно найти КИН и оценить влияние на него различных комбинаций геометрических и физических параметров задачи.
Трещина, коэффициент интенсивности напряжений, фактор влияния, метод интегральных преобразований, сингулярное интегральное уравнение, ядро коши, тонкое покрытие, искусственные нейронные сети, ультразвуковой неразрушающий контроль
Короткий адрес: https://sciup.org/146281962
IDR: 146281962 | УДК: 539.3 | DOI: 10.15593/perm.mech/2019.4.16
Текст научной статьи Идентификация трещиноподобного дефекта и исследование концентрации напряжений в полосе с покрытием
ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2019PNRPU MECHANICS BULLETIN
Эксплуатация деталей машин и конструкций происходит в условиях возникновения коррозии, больших нагрузок, повышенного изнашивания, когда концентраторы напряжения сосредоточены в поверхностных слоях изделия. Передовые технологии покрытия изделий тонкими накладками призваны повысить коррозионную стойкость, твердость, увеличивают надежность и их эксплуатационные сроки за счет создания на поверхности остаточных напряжений сжатия. Кроме этого метода, повысить износостойкость и увеличить прочность возможно за счет создания соответствующих технологий обработки или использования композиций сплавов. Указанные способы позволяют сохранить пластичность и устойчивость к внутренним трещинообразным включениям, повышают сроки эксплуатации изделий и снижают расход металла.
Тонкое покрытие представляет собой слой материала, нанесенного на поверхность детали. Толщина покрытия может достигать от десятых долей до сотен микрометров. Материалами покрытий могут быть лаки, краски, металлы, оксиды, полимеры. Выбор материала покрытия и его толщины зависит от назначения детали и покрытия, технологии ее изготовления и условий эксплуатации и строго регламентируется.
Впервые исследование влияния тонких накладок, изгибной жесткостью которых можно пренебречь, представлено в работах [1–4]. В.М. Александров и С.М. Мхитарян изучили и обобщили результаты исследований многих авторов по контактным задачам для тел с тонкими покрытиями и прослойками [5]. В работе [6] проведено исследование смешанной задачи о передаче нагрузки от стрингеров к упругой полосе, содержащей трещиноподобный дефект. Исследования, представленные в работах [7–9], посвящены решению смешанных задач для составных тел, ослабленных трещинами. В работе [10] решена задача о взаимодействии бесконечного или конечного стрингера с упругой полуплоскостью, содержащей вертикальный разрез. Решению задачи о поперечной трещине в полосе, усиленной ребрами жесткости на обеих гранях, посвящена работа [11].
Проведен ряд исследований, посвященных изучению задач о концентрации напряжений в окрестностях вершин поперечных трещин в полубесконечных упругих телах для различных граничных условий; результаты представлены в работах [12–15].
В работах [16–20] представлены исследования, посвященные изучению концентрации напряжений в окрестностях вершин внутренних трещин в упругих телах (полуплоскость, кольцо, клин), подкрепленных тонкими покрытиями.
Отдельная глава данной работы посвящена локации и идентификации геометрических параметров дефектов в полосе с применением методов конечноэлементного моделирования, ультразвукового неразрушающего кон- троля и технологий машинного обучения (искусственных нейронных сетей).
В работе [25] авторы проводят исследование композитных материалов с дефектами. Из-за наличия дефектов в композитах их эксплуатационные свойства могут ухудшаться. В каждой точке исследуемого объекта проводится ультразвуковое сканирование. Колебания оцифровываются, и затем из них извлекаются характеристики, содержащие информацию об объекте контроля. После проведения анализа данных полученные характеристики классифицируются с применением искусственных нейронных сетей. В результате авторы получают изображение в области дефекта с помощью специально обученной ИНН, которое отражает характер и степень распространения дефекта. Примененный подход четко идентифицирует область повреждения, и полученное изображение совпадает с визуальными наблюдениями.
В работе [26] предложен отличающийся от ранее известных алгоритм многопараметрической идентификации дефектов в стержневых конструкциях. Новизна алгоритма заключается в том, что процедура идентификации дефектов разделена на два этапа: на первом этапе происходит локация дефекта, а на втором этапе происходит оценка степени поврежденности дефекта. В качестве дополнительной информации к решению задачи реконструкции дефектов выступает набор собственных частот и форм колебаний исследуемого объекта. Анализ форм колебаний позволяет решить задачу первого этапа, после чего строится аналитическая или конечноэлементная модель конструкции с дефектами, и с помощью прямых расчетов решается задача второго этапа. В работе также приведен пример расчета параметров дефекта в упругом консольном стержне на основе эксперимента в конечно-элементном комплексе.
В работе [27] применяется один из методов неразрушающего контроля, а именно метод акустической эмиссии, который является весьма перспективным методом оценки композиционных материалов. Для надежного автоматического контроля повреждений с помощью пленочных датчиков поливинилиденфторида (PVDF) важно идентифицировать сигналы акустической эмиссии, связанные со структурой волокон, при наличии шума. В проведенных экспериментах композиты из многослойного армированного стекловолокна (GFRP) были изготовлены несколькими различными способами. Сигналы акустической эмиссии были сняты с поверхности, покрытой PVDF-пленкой, во время статической нагрузки на растяжение. Сигналы акустической эмиссии классифицировались с использованием искусственной нейронной сети. При этом результаты показывают, что различные механизмы разрушения в композитах могут быть классифицированы с применением аппарата искусственных нейронных сетей.
В работе [28] авторы исследуют обрушения, происшедшие во время раскопок туннелей в тонких и чрезвычайно тонких слоистых породах горной породы на гидроэлектростанции Wudongde в Китае. Для прогнозирования риска и глубины обрушения необходим надежный метод, который и предлагают авторы работы. Однако теория и практика показывают, что один-единст-венный критерий не может точно предсказать глубину обрушения. В данной работе с использованием искусственной нейронной сети (ИНС) был исследован метод интеллектуального прогнозирования. На основе теоретического и статистического анализа были выбраны и использованы шесть входных параметров (глубина покрытия, отношение основных малых напряжений, индекс геологической силы, метод выемки грунта, сила поддержки и ориентация породы). Полученные из туннелей данные на гидроэлектростанции Wudongde, а именно сорок пять учебных образцов и шесть пробных образцов, были использованы в обучении модели. Структурные параметры и начальные веса искусственной нейронной сети были оптимизированы с помощью генетического алгоритма. Затем обученная модель была использована для прогнозирования глубины обрушения нескольких участков раскопок. Прогнозы показывают хорошее соответствие с измерениями на участках.
В работе [29] рассматриваются методы инфракрасной термографии, которая является одним из наиболее эффективных методов неразрушающего контроля для диагностирования электрических компонентов с помощью интеллектуального анализа дефектов. Ошибки в электрической системе показывают перегрев компонентов, который является общим показателем плохого соединения, перегрузки, дисбаланса нагрузки или любого дефекта. Термографический контроль используется для поиска проблем, связанных с нагревом, и возможным выходом из строя системы. Однако автоматическая диагностическая система, предложенная авторами работы, основанная на искусственной нейронной сети, сокращает время работы, усилия человека, а также повышает надежность системы. Здесь статистические характеристики, полученные с объектов контроля, и искусственная нейронная сеть используются для проверки электрических компонентов. При этом их термические показатели делятся на два класса – нормальные и перегретые.
В работе [30] представлен альтернативный метод максимального прогнозирования осаждения земной поверхности, основанный на интеграции между вейв-лет-теорией и аппаратом искусственных нейронных сетей. Любой прогноз, полученный с применением методов численного анализа, сильно зависел от модели, принятой для моделирования поведения почвы. Однако создание реалистичной модели, которая могла бы рассчитывать профили установки, связанные с туннелированием, довольно сложно. Большинство исследований показывают, что способность ИНС к распознаванию образов применима в инженерно-геологических задачах, учитывая их успешное применение без каких-либо ограничений. Авторы применяют Wavenet – сеть прямого распространения ошибки с одним скрытым слоем, использующую вейвлеты в качестве функций активации. В данном исследовании применяются различные вейвлеты в качестве активационных функций для прогнозирования максимального поверхностного осаждения в процессе туннелирования. Результаты моделирования указывают на уменьшение значений ошибки оценки, что отражает их способность повышать функциональную аппроксимирующую способность и, следовательно, демонстрирует отличную способность к обучению по сравнению с обычной нейронной сетью обратного распространения с сигмоидной или другими функциями активации.
В работе [31] авторами предлагается ранняя диагностика неисправностей в коробке передач, чтобы определить состояние зубчатой передачи на основании сигналов вибрации, полученных от экспериментальной испытательной установки. В предлагаемой работе для извлечения статистических признаков используется обработка сигналов, отнесенная к частотно-временной области, – непрерывное вейвлет-преобразование. Метод поиска особенностей используется для выбора полезных функций среди извлеченных, чтобы сократить время обработки. Такой известный метод оптимизации, как генетические алгоритмы, используется для выбора лучших входных функций с целью уменьшения вычислительной нагрузки. Эффективность этого метода оценивается на основании точности классификации, полученной с помощью таких технологий, как нейронные сети обратного распространения (BPNN) и C4.5. Производительность классификаторов оценивается с помощью различных сигналов, полученных от экспериментальной испытательной установки для различных состояний шестерен.
В работе [32] авторами проводится моделирование системы неразрушающего контроля дефектов в твердых телах. Рассматриваются обратные геометрические задачи теории упругости для плоской прямоугольной области по реконструкции круговых полостей и трещин, выходящих на поверхность тела. В качестве дополнительной информации для решения этих задач авторы используют набор первых четырех собственных резонансных частот. Решение обратных задач основано на минимизации функционала невязки между измеренной входной информацией и рассчитанной в ходе численного решения прямых задач с заданными параметрами дефектов.
В работе [33], на основе данных о протекании вихревых токов, предложены несколько методов классификации дефектов, среди которых, и различные ИНС схемы. В качестве исходной информации, поступающей в ИНС, используются данные об изменении электрического импеданса прошедшие обработку Фурье и вейвлет преобразованиями.
В работе [34] с помощью ИНС виде стандартного многослойного персептрона разработан метод автоматического определения дефектов во время мониторинга токопроводящих конструкций на основе измерения вихревых токов. Для выделения характерных особенностей, измеренного электрического сигнала, поступающих на вход ИНС, применяются различные методы: в том числе, вейвлет и Фурье преобразования, анализ главных компонент и др., отмечаются их преимущества.
1. Идентификация дефектов
Своевременная диагностика, прогнозирование и идентификация дефектов является необходимым мероприятием, способным предотвратить многие негативные последствия, которые могут возникнуть в результате отказа и выхода из строя как элементов конструкций, так и систем в целом. Среди методов неразрушающего контроля ведущее положение занимает ультразвуковой контроль. Он основан на способности звуковых волн отражаться от границы раздела двух упругих сред, обладающих разными акустическими свойствами. В наших предыдущих работах [22–24] мы исследовали некоторые методы неразрушающего контроля в сочетании с технологиями искусственных нейронных сетей в области идентификации дефектов.
Постановка прямой и обратной задач. В прямой задаче рассматриваются вынужденные колебания упругого тела, которые описываются следующей краевой задачей:
c ч , j = p u i ; c ij = c ijki u k , i , i = 1,2,3, (1)
U I s u = ^ , ° j n j I S t = P i , C ij n j I S d = qt , (2)
(°) где ui – искомые компоненты вектора смещений; ui и pi , qi – известные компоненты вектора смещений и поверхностных нагрузок; ст у и cijkl - компоненты тензоров напряжения и упругих постоянных; р - плотность; Su, St – поверхности тела, на которых задан вектор смещений и напряжений соответственно; Sd – внутренние поверхности туннельной трещины в направлении оси Ox3.
В задачах идентификации дефектов (трещин, включений, полостей) требуется определить их конфигурацию, поэтому поверхности Sd являются неизвестными, что относит рассматриваемые проблемы к обратным геометрическим задачам теории упругости. Далее будем считать, что берега трещины не взаимодействуют и свободны от напряжений q i = °. Для решения обратных задач реконструкции поверхности Sd необходима некоторая дополнительная информация кроме той, что содержится в краевых условиях (2). Такой дополнительной информацией может быть амплитудно-временная характеристика (АВХ) волнового поля смещений U измеренного на свободной поверхности:
u i = Ut ( x;k,t ) , при t e [ °, T ] и k = 1, 2,..., n, Xkk e S t (3)
где Т – характерное время отражения сигнала; n – количество точек измерения.
Таким образом, получаем набор входной информации X , который может быть использован в методе реконструкции геометрических параметров трещины.
Параметры конечноэлементной модели. Рассматривается задача идентификации дефектов в виде прямолинейной трещины в полосе, поверхность которой усилена тонкой накладкой. Параметры конечноэлементной модели:
Толщина полосы ........................................................ 20 мм
Ширина полосы ......................................................... 30 мм
Ширина PML слоев ................................................... 13 мм
Толщина покрытия ................................................. 0,25 мм
Материал полосы............сталь ( E = 210 ГПа, v = 0,28 )
Материал покрытия .............................................вольфрам
( E = 350 ГПа, v = 0,29)
Толщина полосы установлена таким образом, что превосходит длину ультразвукового импульса. Это позволяет наиболее точно регистрировать форму колебаний отраженного сигнала. Толщина покрытия соответствует толщине покрытий из карбида вольфрама, нанесенных методом газопламенного напыления (100– 300 мкм). Подобрана наиболее рациональная ширина PML-слоев, которые предотвращают отражение сигнала от правой и левой границ полосы на протяжение всего времени расчета.
На рис. 1 изображена полоса с покрытием, по обе стороны которой расположены слои PML. Полоса имеет внутренний разрез, который моделирует трещину. Верхняя и нижняя границы полосы свободны. Левая и правая границы PML блоков закреплены.
Слои PML заданы как бесконечные элементы. Они предназначены для моделирования распространения ультразвуковой волны в полосе без отражений от ее границ справа и слева. Бесконечные элементы COMSOL применяют полубесконечное координатное растяжение в одном, двух или трех направлениях, в зависимости от того, как область бесконечного элемента соединяется с физической областью. В каждом направлении используется одна и та же форма растяжения, определяемая как функция безразмерной координаты ^, которая из- меняется от 0 до 1 вдоль бесконечного элементного слоя. Функция возвращает новую, растянутую координату, интерпретируемую как новая позиция в заданном направлении. То есть смещение для растяжения в одном направлении Ах = f (£)-Аw^, где Aw - исходная ширина области бесконечного элемента (как показано на рис. 1). Отдельный вектор смещения вычисляется для каждого направления растяжения и суммируется для получения полного смещения. Функция растяжения по умолчанию определяется как
f(^ = т^Аp ,где А p - Ч-Ч
так называемое расстояние полюса; у - число больше единицы, вычисленное как у = (Аs + Ap) / Аs, где As - масштабированная толщина области бесконечного элемента.
Ультразвуковой сигнал частотой 2 МГц представлен в виде отрицательной функции синуса с примененной к ней функцией окна Хеннинга. Входной сигнал создается на основе ранее сгенерированных данных с применением линейной интерполяции и представлен функцией Impulse (t). Область ввода ультразвукового сигнала представлена совокупностью точек на поверхности покрытия, расположенных на отрезке длиной 3 мм. Зондирующий импульс задается смещением узловых точек, на поверхности покрытия u0 = Impulse (t).
С учетом скорости звука в стали и вольфраме и частоты зондирующего импульса длины волн в материалах полосы и покрытия соответственно: Хсталь = 0,002975м, ^вольфрам = 0,002587 м. Размер конечного элемента Ах max Хсталь /16 = 0,000185 м. Время шага max
А t к р
C сталь
3,12 -10 8 с. Время, в течение которого моделируется распространение ультразвуковой волны,
2 - 10 - 5 с.
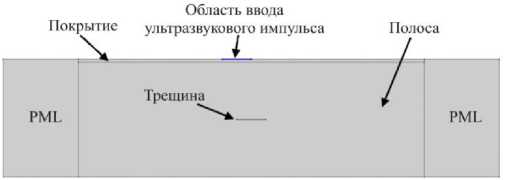
Рис. 1. Схематичное изображение модели полосы с покрытием
Fig. 1. Schematic representation of the coated bar model
Для моделирования распространения ультразвуковой волны применяется конечно-элементный комплекс COMSOL с модулем Solid Mechanics в режиме Time Dependent. Интерфейс Solid Mechanics основан на решении уравнений движения с учетом определяющей модели твердого материала. При этом вычисляются перемещения, напряжения и деформации. Режим Time Dependent используется, когда переменные поля меняются со временем. В механике твердого тела он используется для расчета изменяющейся во времени деформации и движения твердых тел, подверженных переходным нагрузкам. При этом применяется Time-Dependent решатель, который использует обобщенную α-схему (generalized-α) интегрирования. Обобщенная α-схема изначально была разработана для проведения структурного анализа методом конечного элемента. Она обеспечивает простую и эффективную реализацию, а также оптимальное сочетание точности при низких частотах и численного демпфирования при высоких частотах. Эта особенность интересна тем, что позволяет исключить влияние нефизических высокочастотных мод, которые обычно присутствуют в конечно-элементных моделях
[35]. Геометрия построенной модели разбивается на небольшие элементы треугольной формы. В области дефекта и источника зондирующего импульса сетка конечных элементов сгущается.
Конечноэлементное моделирование. В рамках поставленных задач было проведено определенное количество расчетов моделей при различных параметрах трещиноподобного дефекта. Для каждой конфигурации геометрических параметров дефекта проводится моделирование распространения ультразвуковой волны, источник которой расположен в четырех различных точках. Эти точки равномерно распределены на отрезке, находящемся на поверхности покрытия над дефектом. Таким образом, ультразвуковой импульс может частично или полностью отражаться от берегов трещины, что можно видеть на рис. 2.
Конфигурация геометрических параметров определяется длиной трещины l и варьируется в пределах от 1 до 5 мм (всего 10 значений), глубиной залегания дефекта y 0 и определяется значениями от 2 до 8 мм (всего
5 значений), а также толщиной h дефекта в пределах от 0,1 до 0,5 мм (всего 10 значений).
В результате проведения расчетов модели были получены временные характеристики ультразвукового эхо-сигнала, для каждой конфигурации дефекта. На рис. 3 и 4 показаны амплитудно-временная характеристика ультразвукового сигнала и соответствующая ей амплитудно-частотная характеристика.
Применение искусственных нейронных сетей. Нейронные сети – это инструмент нелинейного моделирования. Обычно они используются для моделирования сложных связей между входами и выходами для нахождения закономерностей в данных. В рамках данной задачи необходимо установить связь между амплитудновременной характеристикой ультразвуковой волны, распространяющейся в полосе, и конфигурацией дефекта. На основе полученных данных на этапе конечноэлементного моделирования возможно сформировать обучающий набор и провести обучение построенной модели нейронной сети.

Рис. 2. Распространение и отражение ультразвуковой волны при различных положениях источника сигнала
Fig. 2. Propagation and reflection of the ultrasonic wave at different positions of the signal source
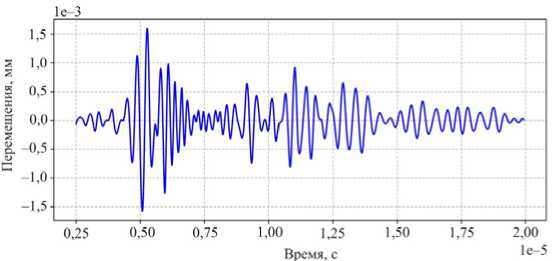
Рис. 3. Амплитудно-временная характеристика распространения ультразвуковой волны в полосе; трещина расположена горизонтально, толщина h = 0,5 мм, глубина залегания y 0 = 1 мм, длина l = 1 мм
Fig. 3. Amplitude-time characteristic of ultrasonic wave propagation in the bar, the crack is horizontal, the crack thickness is h = 0,5 mm, depth is y 0 = 1 мм, crack length is l = 1 mm
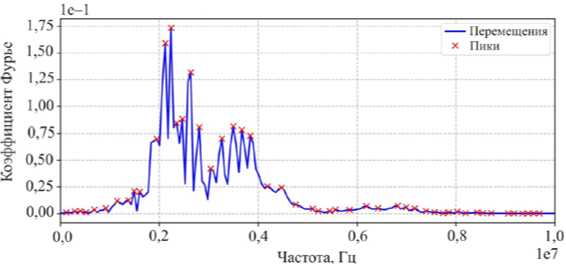
Рис. 4. Амплитудно-частотная характеристика ультразвуковой волны в полосе; трещина расположена горизонтально, толщина h = 0,5 мм, глубина залегания y 0 = 1 мм, длина l = 1 мм
Fig. 4. Amplitude-frequency characteristic of ultrasonic wave propagation in the bar, the crack is horizontal, the crack thickness is h = 0,5 mm, depth is y 0 = 1 mm, crack length is l = 1 mm
Для получения амплитудно-частотных характеристик колебаний исследуемого объекта применяется дискретное преобразование Фурье (ДПФ). В качестве входной информации для нейронной сети выступают значения пиков амплитуд и соответствующих им частот (рис. 4). Для каждой амплитудно-частотной характеристики выбирается 50 пар значений. Таким образом, для четырех сканирующих ультразвуковых импульсов формируется входной вектор, состоящий из 400 значений. Каждому вектору соответствует выходной набор данных, состоящий из геометрических параметров дефекта l , y 0 , h . Итоговый набор данных состоит из 2000 обучающих векторов, 1500 из которых применяются для обучения нейронной сети, а остальные 500 для валидации.
Применяется искусственная нейронная сеть прямого распространения. Установлено, что наиболее рациональная архитектура нейронной сети содержит 400 входных значений, два скрытых слоя по 200 нейронов в каждом и 3 выходных значения. В качестве алгоритма обучения применяется SGD (Stochastic gradient descent). Наилучший результат работы сети достигается при 1530 итерациях обучения. Нейронная сеть построена на основе фреймворка Keras.
Результаты идентификации геометрических параметров дефектов. На основе обученной нейронной сети возможно провести идентификацию дефекта в полосе. На вход нейронной сети подаются данные из валида-ционного набора. Эти данные не принимали участия в процессе обучения. На рис. 5 показана ошибка идентификации параметра y 0 глубины залегания дефекта.
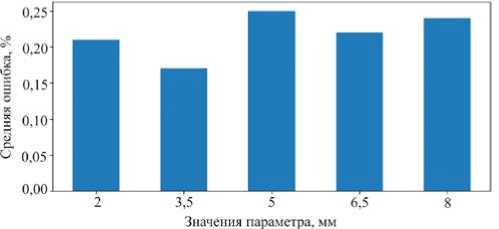
Рис. 5. Ошибка идентификации параметра глубины залегания дефекта, 0,22 %
Fig. 5. Error of identification of the defect depth parameter
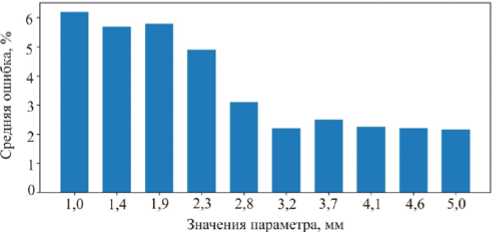
Рис. 6. Ошибка идентификации параметра размера дефекта, 3,7 %
Fig. 6. Error of identification of the defect length parameter
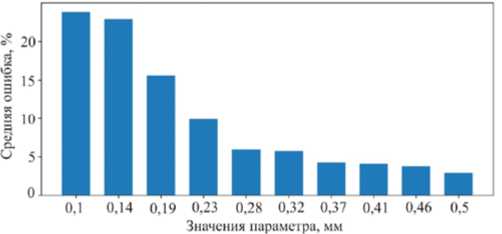
Рис. 7. Ошибка идентификации параметра толщины дефекта, 9,89 %
Fig. 7. Error of identification of the defect thickness parameter
На рис. 6 показана ошибка идентификация параметра l длины трещины. Из графика видно, что для больших величин параметра идентификация проходит более успешно. На рис. 7 показана ошибка идентификации параметра h -толщины дефекта. Видно, что наиболее успешная идентификация достигается при значении параметра, близком к максимальному из рассматриваемых в рамках данной задачи.
2. Исследование концентрации напряжений в окрестности вершин трещины в полосе с тонким покрытием
Комплексный подход к решению проблемы исследования напряженно-деформированного состояния тел, содержащих внутренние дефекты, включает два основных аспекта. Первый из них – идентификация дефектов с целью использования информации о них для предупреждения разрушения – один из самых важных аспектов в рамках эксплуатационной безопасности и функциональности рассматриваемых объектов. Эта проблема относится к области неразрушающего контроля, и ее решению посвящена основная часть настоящей работы. Другим, не менее важным, аспектом заявленной проблемы является исследование их напряженно-деформированного состояния, определение зон и интенсивности концентрации напряжений, обусловленных наличием дефектов. После того как решена задача идентификации типа дефекта и его геометрических характеристик, решается проблема второго шага. В частности, решение этой прямой задачи и исследование локального поля напряжений в окрестности особых множеств границы дефекта может быть проведено численно, с использованием МКЭ, или аналитическими методами.
Опишем технологию применения аналитикочисленного метода на примере задачи, постановка которой отличается от рассматриваемой в настоящей работе тем, что покрытие находится как на верхней, так и на нижней плоскости. Такая статическая задача теории упругости для полосы, ослабленной прямолинейной продольной трещиной, расположенной симметрично относительно границ, рассмотрена ранее в [20].
В направлении, перпендикулярном линии трещины, приложены нормальные растягивающие усилия, обеспечивающие ее раскрытие. Граница полосы подкреплена тонким упругим покрытием . На бесконечности реализуются условия затухания компонент вектора перемещений и тензора напряжений. Покрытие полосы свободно от напряжений. В силу симметрии задачи рассматривается область верхней части полосы. Построено решение уравнений равновесия в перемещениях для задачи плоской деформации.
На верхней грани полосы действуют граничные условия, моделирующие влияние накладки [16, 20], которые сформулированы на основании проведенного асимптотического анализа решения задачи для тонкой упругой полосы [5]. Их адекватность установлена серией численных экспериментов, проведенных в [16]. Общее решение системы дифференциальных уравнений для полосы построено с помощью преобразования Фурье. Сингулярное интегральное уравнение задачи построено путем удовлетворения граничному условию на берегах трещины. В результате получено сингулярное интегральное уравнение с ядром Коши. Проведено сравнение полученного интегрального уравнения при нулевой толщине покрытия с аналогичным уравнением, представленным в монографии [21].
Решение полученного интегрального уравнения строится методом коллокаций в виде линейной комбинации базисных функций, явно учитывающим особенность в окрестности вершин трещины. В результате получены значения коэффициента интенсивности нормальных напряжений KI в окрестности вершин трещины. Проведено исследование влияния свойств некоторых материалов покрытия на фактор влияния N ( ± 1 ) (приведенный коэффициент интенсивности нормальных напряжений) от параметра X, характеризующего относительное расстояние трещины до границы раздела. N ( ± 1 ) = K I / K I „ , K I т - соответствующая величина (в классическом случае) изолированной прямолинейной трещины в упругой плоскости. В качестве материала полосы рассматривается конструкционная сталь. Материалы накладок – тефлон, алюминий, титан, никель, хром, нитрид титана, вольфрам, карбид вольфрама, то есть как более жесткие, так и более мягкие материалы по сравнению с материалом самой полосы.
В частности, установлено, что чем мягче материал накладки, тем меньше его влияние на раскрытие трещины, причем увеличение толщины накладки для мягких материалов не является сдерживающим фактором. Если материал накладки более жесткий, чем материал полосы, накладка оказывает сдерживающее влияние, причем чем больше ее толщина, тем больше влияние.
Заключение
Целью исследования является разработка комплексного подхода к определению локального напряженного состояния в окрестности особых множеств внутренних дефектов, локация которых заранее неизвестна. Предложенный подход основан на двух этапах решения проблемы: идентификация типа и размера дефекта; определение КИН в вершинах трещины. Первая задача решается на основе сочетания ИНН и МКЭ. Для этого построена конечно-элементная модель распространения ультразвуковой волны в полосе, усиленной покрытием. На основе накопленных данных создана и обучена нейросетевая модель, позволяющая проводить идентификацию геометрических параметров внутреннего трещиноподобного дефекта.
Исследования показали, что возможно успешное применение нейросетевых технологий в сочетании с методами ультразвукового неразрушающего контроля в рамках решения задачи идентификации трещиноподобных дефектов в полосе, усиленной покрытием. При этом предложенная модель искусственной нейронной сети проводит идентификацию глубины залегания дефекта с точностью 0,22 %, длины дефекта с точностью 3,7 %, толщины дефекта с точностью 9,89 %.
Второй этап предполагает решение прямой задачи с известным дефектом и исследование локального НДС в его окрестности. Описана технология аналитикочисленного решения задачи второго этапа на примере подобной статической задачи. В частности, описана процедура определения значений фактора влияния – приведенного коэффициента интенсивности напряжений в окрестности вершин трещины, анализа влияния геометрических и физических параметров задачи на величину исследуемого параметра. Это позволило сделать следующие выводы: увеличение толщины и жесткости покрытия ведет к снижению фактора влияния; увеличение длины трещины или уменьшение ширины полосы влечет за собой увеличение фактора влияния.
Работа выполнена при поддержке Российского фонда фундаментальных исследований в рамках проектов 19-08-0074, 18-31-00024.
Список литературы Идентификация трещиноподобного дефекта и исследование концентрации напряжений в полосе с покрытием
- Melan E. Zur plastizität des räumlichen kontinuums // Archive of Applied Mechanics. - 1938. - No. 9/2. - S. 116-126.
- Рейсснер Э. Некоторые проблемы теории оболочек. Упругие оболочки. - М.: Изд-во иностр. лит., 1962. - 263 с.
- Koiter W., Warner T. On the nonlinear theory of thin elastic shells // Koninklijke Nederlandse Akademie van Wetenschappen. - 1966. - No. 69.1. - P. 1-54.
- Развитие теории контактных задач в СССР / под ред. Л.А. Галина. - М.: Наука, 1976. - 493 c.
- Александров В.М., Мхитарян С.М. Контактные задачи для тел с тонкими покрытиями и прослойками. - М.: Наука, 1979. - 486 с.


