Идентификация утечек тока в распределительных сетях по данным АСКУЭ

Широкое внедрение автоматизированных систем контроля и учета электроэнергии (АСКУЭ) в распределительных электрических сетях (РЭС) [1] ставит перед их разработчиками новые задачи, решение которых направлено на дальнейшее повышение их эффективности и экономических показателей распределительных компаний. Как известно, АСКУЭ представляет собой информационно-измерительную систему, предназначенную для выполнения функций оперативного сбора данных с группы счетчиков электроэнергии (Сч), установленных у абонентов сети, их хранение и обработку измерительной информации с целью коммерческого учета электроэнергии. Обмен данными между функциональными элементами системы осуществляется с использованием современных телекоммуникационных технологий (PLC, GSM и др.). Анализ структуры внедряемых в настоящее время АСКУЭ показывает, что в их составе нет функциональных подсистем, обеспечивающих решение таких важных задач, как мониторинг потерь электроэнергии [2–4], диагностика состояний трехфазной сети [5–8] и симметрирование фазных нагрузок, обеспечивающих оптимизацию функционирования РЭС [9–13]. В то же время их решение, в частности, решение задач диагностики распределительных сетей в режиме реального времени требует разработки соответствующих математических моделей и методов, ориентированных для использования в составе АСКУЭ. Основная трудность при этом заключается в том, что практически большинство РЭС имеют сложную струк- туру, функционируют в условиях несимметрии токов и напряжений [14–16], а также подвержены действию случайных внешних возмущающих факторов, приводящих к значительным техническим и коммерческим потерям электроэнергии. К таким возмущениям, в частности, относятся утечки токов в трехфазной РЭС, вызванные различными внешними факторами, включая подключение к сети несанкционированных потребителей электроэнергии [17, 18]. В этих условиях решение указанных выше задач на основе известных моделей и методов анализа и идентификации параметров трехфазной сети (методы симметричных составляющих, графов и др.) [19–23] связано с большими трудностями. Методологические основы идентификации и локализации несанкционированного отбора электроэнергии в распределительной сети изложены в [18, 24]. В данной статье дано развитие этих результатов и предложен метод идентификации координаты мест отбора тока утечки в РЭС с использованием простых вычислительных процедур.

Постановка задачи

Рассматривается четырехпроводная трехфазная сеть с напряжением 0,4 кВ, расчетная схема которой показана на рисунке.

На рисунке k,v - индексные переменные, обознача ющ ие соответственно номера фаз А, В, С (k = 1,3) и электрических контуров сети (v = 1,и); I_vk , U_vk - синусоидальные мгновенные ток и напряжение на соответствующем электроприемнике (нагрузке) с координатой ( v , k); i_vk, z_vk -

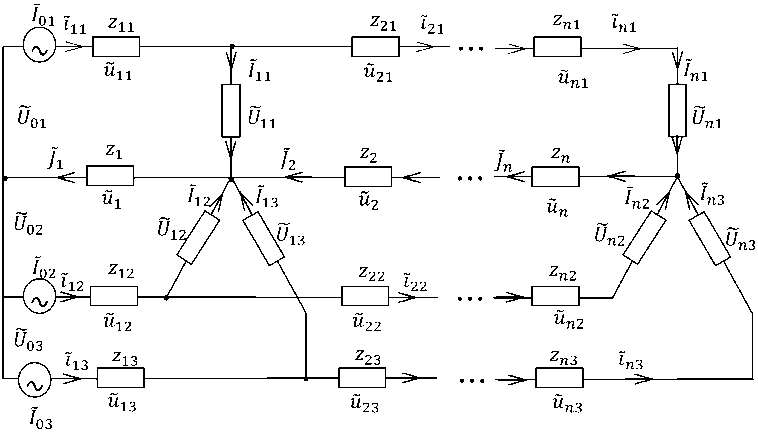
Расчетная схема трехфазной сети

мгновенный ток и сопротивление ν -го межабонентского участка (МАУ) к-й фазы; H_vk , H_v - напряжения соответственно на v -м МАУ к-й фазы и нейтрального провода; J_v , z_v - мгновенный ток и сопротивление ν -го участка нейтрального провода; U_ok , I_ok — мгновенные синусоидальные напряжения и токи соответственно на входах соответствующих фаз.

Далее предполагается, что выполняются следующие условия:

• 1.    Распределительная сеть функционирует в несимметричном режиме.

• 2.    Токи утечек, включая токи несанкционированных потребителей (нагрузок), отводятся через токопроводящие элементы, минуя нейтральный провод.

• 3.    Линейные и нейтральный провода сети имеют разные сечения.

• 4.    База данных АСКУЭ содержит текущие значения сопротивлений z_vk и z_v межабонентских участков (МАУ), представленных в комплексной форме [6, 15].

• 5.    Периодически в дискретные моменты времени t Е [t ^ , t ^ ₊₁] подсистема сбора данных АСКУЭ осуществляет опрос абонентских счетчиков электроэнергии ( Сч_vk ) с шагом дискретизации At ^ = t ^ ₊₁ — t ^ , где f = 1,2, ... . На основе измерительной информации в автоматизированной системе формируются исходные данные задачи – подмножества I_t , U_t и ф_t , состоящие из действующих токов I_vk и напряжений U_vk на соответствующих нагрузках и сдвигов фаз ф_vk между ними:

• 6.    В АСКУЭ на основе исходных данных, т. е. компонентов подмножеств I_t , U_t и ф_t , в оперативном режиме осуществляется комплексное представление переменных, описывающих состояния электроприемников (нагрузок) сети:

^It    ^{Ivk } n х 3 , ^Ut    ^{Uvk } n х 3 , Ф t     £^ vk } n х 3 ^.

I vk = Ivk +jI ^k = W^)Ct^ ,

Uvk = UVk+jUVk = Uvke^, (1) v = 1^,k=T3, где символы «в» и «м» здесь и далее обозначают вещественные и мнимые части соответствующих комплексных переменных; Ivk, Uvk, avk, ^vk - модули (действующие токи и напряжения) соответствующих комплексных переменных и их фазовые сдвиги соответственно; j = ^—1 - мнимое число. Численный алгоритм представления состояний нагрузок сети в форме (1) предложен в [15].

В каждый момент времени t Е [t ^ , t ^ ₊₁] суммарные токи на входах фаз I_k (t) (к = 1,3), потребляемые абонентами сети в соответствующих фазах, определяются выражениями:

№ = Х П ₌₁ kk(t), к = T3. (2)

Далее будем считать, что распределительная сеть в момент наблюдения t Е [t ^ , t ^ ₊₁] находится в номинальном (нормальном) состоянии S ⁰ , если отсутствуют утечки токов. Такое состояние сети в дальнейшем назовем ее желаемым состоянием S ⁰ . При этом выполняются следующие условия:

|I ok (t)- TOI <  AI max , k = T3, (3) где I_ok(t) - действующий ток на входе к -го линейного фазного провода, измеряемый счетчиком электроэнергии (Сч) на выходе источника питания – трансформаторной подстанции (ТП); где AI_max - максимально допустимая погрешность измерения токов.

При появлении в распределительной сети возмущения в виде утечки тока не выполняется хотя бы одно из условий (3). Такое состояние сети в дальнейшем назовем ее возмущенным состоянием S ’. Величины тока утечки AI_k(t) в -й фазе сети можно вычислить по формуле

Ai k (t) = I ok (t) — I k (t), к = Тз, (4)

где /k(t) - сумма абонентских токов в соответствующей фазе, которая определяется выражением (2).

Для определенности далее предположим, что в некоторый момент наблюдения t Е [t ^ , t ^ ₊₁] в РЭС обнаружен факт наличия в сети одного возмущения в виде утечки тока, действующего в фазе с номером ц, где ц ЕМ, а М — {1,2,3} - дискретное подмножество, состоящее из трех элементов, обозначающих номера фаз сети. При этом комплексный ток утечки Д/_м в соответствии с выражением (4) определяется выражением:

• ■             ■               ■ _

Д/ м = / ом — #•                             (5)

Место утечки тока делит линейный провод μ-й фазы на две части соответственно с длинами Z_1M и ^_2м, где ^_1м отсчитывается от источника питания (ТП). Поэтому величину 1_1м можно принять за координату места отвода тока утечки. При этом общая длина 1_м линейного провода и его общее сопротивление Z_M определяются по следующим формулам:

• ^ М ^— ^ 1М ⁺ ^ 2м , ^ZM ^{— Z}1M ^{+ Z}2m ,

где Z2M — длина МАУ от места отвода тока утечки Д/k(t) до конечного электроприемника; Z1M,Z2M — сопротивления соответствующих участков рассматриваемого линейного провода, представляемые в комплексной форме:

Z 1M = Z ? M + № Z m = Z M + ;Z м .

Задача заключается в идентификации (локализации) места отвода тока утечки в сети, т. е. координату 1 1м .

Метод решения задачи

Основная идея предлагаемого метода базируется на математическом моделировании возмущенного S ' и желаемого S ⁰ состояний трехфазной сети при наличии утечек тока. Далее с использованием модели идентифицируются межабонентские токи i V _k, а также фактическое Дй_м и потенциально (максимально) возможное й_тахм приращения напряжений на линейном проводе возмущенной -й фазы, вызванные током утечки Д/_м. На основе результатов такой идентификации формируются аналитические соотношения, описывающие функциональные связи между указанными приращениями напряжений и параметрами соответствующего линейного провода Z_1M и Z_M. Полученные соотношения далее используются для формирования алгебраического уравнения, решение которого позволяет определить место утечки тока в сети, т. е. величину 1_1м .

В соответствии с изложенным решение сформулированной выше задачи включает следующие основные этапы:

• 1)    оценка межабонентских токов и напряжений в желаемом состоянии сети S ⁰ ;

• 2)    оценка приращений напряжений в возмущенном состоянии сети S*;

• 3)    идентификация (локализация) координаты места отвода тока утечки.

Оценка межабонентских токов и напряжений в желаемом состоянии сети S ⁰ . Для этой цели рассмотрим ситуацию, когда трехфазная сеть находится в нормальном состоянии S ⁰ . В этом случае отсутствует утечка токов (Д/_k — 0, к — 1,3) и выполняются условия (3). Тогда на основе комплексного представления (1) и первого закона Кирхгофа можно вычислить межабонентские токи i ° _k и токи в нейтральном проводе /V по следующим формулам [6, 15]:

iOk = ^^iik = ^^(iik+HTk),(6)

v — Т/п, к — 13;

/о _ -о , -о  ,  -о _

JV — lV1 + lV2 + lV3, v — 1, н.

По условиям задачи комплексные сопротивления z_VM и z_v МАУ -й фазы являются известными величинами. Тогда выражения (6) и (7) позволяют вычислить соответствующие напряжения u j° _M на межабонентских участках по следующим формулам:

u Vm — i Vm^zv , v — Т/й.                       (8)

При этом напряжение й у _м на -м линейном проводе в желаемом состоянии сети S ⁰ определяется как сумма потерь напряжений на его участках:

^й£м^— ^ "=1^ ,                       ⁽⁹⁾

где величины напряжений u V _M вычисляются по формуле (8).

Оценка приращений напряжений в возмущенном состоянии сети S' . Для этой цели рассмотрим балансовые соотношения для напряжений в контурах рассматриваемой фазы (см. рисунок):

У' . — й ( v+1),m + ^ +1 + U ' (v+1) _№,         (10)

v — 0, и — 1, где й(v+1),M,u'v+1 - комплексные напряжения на (v + 1)-м участке соответственно линейного и нейтрального проводов возмущенной -й фазы.

В выражении (10) известными являются напряжения U ' _V m и У' ( _v+1 ), _ц на соответствующих нагрузках, которые по измерительным данным АСКУЭ предварительно представлены в форме (1). Так как ток утечки Д/_м по условиям задачи отводится в землю, минуя нейтральный провод, то межабонентские токи j_v , протекающие в нейтральном проводе, в желаемом S⁰ и возмущенном S' состояниях сети являются равными, т. е. /V — j_v , где v — 1, и. Поэтому величины напряжений u_v+1 с учетом (7) можно вычислить по формулам:

u ' v —j V z v — ⁽ i °1 + 1 V2 + i V ₃ ^)zv ,v — 1,и.

В результате на основе выражения (10) можно определить напряжения й(У+1),ц на участках линейного провода:

^и(У+1),ц = ^' УЦ -U (у+1), ц ^- u_v +i ,         ⁽¹1)

v = 0,n - 1.

Таким образом величина напряжения и ^ _ц на -м линейном проводе в возмущенном состоянии S ' сети определяется следующим выражением:

й-i ц    E v=i^ ,                        ⁽¹²⁾

где напряжения и Уц вычисляются по формуле (11).

Идентификация (локализация) координаты места отвода тока утечки . Для этой цели вначале определим оценку предельно (максимально) возможного приращения напряжения и_тахц на линейном проводе -й фазы, вызванного током утечки Д/_ц. При этом предполагается, что возмущение в виде утечки тока действует в конце ^-й фазы. В этом случае искомую величину и_тахц можно вычислить по формуле

= м У” _ т =М 7 = итахц ^■‘ц iv=l ^уц   и1ц_ итахц + 7итахц,

где Д/_ц - комплексный ток утечки, определяемый по формуле (5); и т _ахц, и т _ахц — вещественная и мнимая части комплексного напряжения и_тахц. Отметим, что все величины, входящие в выражение (13), по условиям задачи являются известными.

Тогда приращение напряжения Диц на начальном участке μ-го линейного провода длиной <1ц, в котором протекает ток утечки Д/ц, определяется следующей разностью:

Ду = и £ц —й £ц = Д^ м +7 Ди ^ , (14) где суммарные напряжения и 1 _ц и и ^ _ц вычисляются соответственно по формулам (9) и (12).

Так как приращение напряжения Ди_ц, определяемое формулой (14), вызывается током утечки Д1_ц , то можно считать, что

Ду = Д1^ 1ц .

В результате на основе выражений (13) и (15) можно записать следующее алгебраическое соотношение

^Д-^    ^ig * maxg “ Z_M ^.

Введем в рассмотрение модули комплексных величин, входящих в выражение (16):

Дйц _ 7(ДиЦ)2 + (Диц)2, итахц _ V(итахц)2 + (итахц. ^1ц _ J(^lц)2 + (^Гц)2,

/ц_ VW+TW

Легко заметить, что соотношение (14) эквивалентно следующему модульному соотношению:

Ди-^   ^^ig umaxg   ^g

С другой стороны, для модулей сопротивлений справедливы следующие формулы [25]:

^ 1ц ^_ Р ц ^ 1ц ,^ ц ^_ Р ц ^ ц ,                    ⁽¹⁸⁾

где рц - удельное сопротивление -го линейного провода сети.

В результате с учетом (18) соотношение (17) преобразуется в алгебраическое уравнение относительно 1_1ц :

^Д'^iZg    ^ ig “ maxg     lg .

Отсюда искомая координата 1_1ц места отвода тока утечки определяется по следующей формуле:

₇    __ ^{Дг^}g ^ g

¹1ц ^_ 77 ^umaxg

.

Полученные результаты естественным образом можно распространить на случай, когда в каждой фазе распределительной сети имеются утечки тока.

Выводы

Предложен метод идентификации координаты места отвода тока утечки в распределительной сети напряжением 0,4 кВ, функционирующей в условиях несимметрии токов и напряжений с использованием измерительных данных АСКУЭ, полученных с абонентских счетчиков электроэнергии. Основная идея метода базируется на построении математической модели, описывающей возмущенное и номинальное (желаемое) состояния трехфазной сети на основе комплексного представления ее переменных (напряжений, токов) и параметров (сопротивлений). Такой подход позволил идентифицировать приращения напряжений на участках линейного провода, в которых протекает ток утечки. Получены аналитические соотношения, которые дали возможность найти функциональные связи между этими приращениями напряжений и параметрами возмущенной части сети и локализовать координату места отвода тока утечки. Процедура идентификации реализуется на основе простых вычислительных операций. Предложенный метод можно использовать для построения подсистемы диагностики распределительной сети в составе АСКУЭ.