Идентификация веществ по сильно искажённым ошибками измерения спектрам

На сегодняшний день существует большое количество оптических приборов, позволяющих анализировать спектральные свойства света в широком диапазоне длин волн. Часто такие устройства входят в состав систем химического мониторинга окружающей среды. Регистрируемый сигнал содержит полезную информацию, анализ которой позволяет отличать одни вещества от других, тем самым выявлять их присутствие. К примерам можно отнести прибор «FirstDefender RM» фирмы «Ahura Scientific», основанный на Раман-эффекте и позволяющий осуществлять оперативный контроль присутствия опасных для человека веществ на химически вредных предприятиях.

Метод интерпретации зарегистрированных спектров, основанный на сопоставлении их с эталонными, является одним из наиболее распространённых в прикладных задачах спектроскопии. Для этого применяется функция меры схожести, которая характеризует степень совпадения форм экспериментальной и эталонной кривой. Существует большое число выражений, с помощью которых можно задать требуемую меру [1]. Одной из распространённых формул является SAM [1–7] (от англ. Spectral Angle Mapper), которая используется в задачах физики [1–3], машинного зрения [4, 6], фармацевтики [7] и аналитической химии [5].

Анализ влияния шума в зарегистрированном спектре на величину меры схожести SAM проводился ранее в работах [8, 9]. В [8] для определения параметров распределения величины SAM предлагается использовать метод Fisher z-transformation, см. [10, 11]. А в работе [9] для этих же целей предлагался t-критерий Стьюдента. Оба этих способа являются статистическими, что делает невозможным применение их для проведения экспресс-анализа по одному текущему измеренному спектру.

Цель работы заключается в создании эффективного метода идентификации веществ по спектрам в условиях низкого отношения сигнал/шум в них. Для этого решается задача вывода приближённых аналитических выражений для расчёта параметров распределения используемой меры схожести.

1.    Теория 1.1.    Статистические характеристики нормированного скалярного произведения

Величина нормированного скалярного произведения определяется следующим соотношением:

ρ = ρ ( x , y )=( x , y ) .                               (1)

| x | ⋅ | y |

Если x и y – две непрерывные функции, определённые на интервале частот [ ν нач , ν кон ], то для расчёта скалярного произведения используется выражение:

V кон

( x , y ) = ∫ xy d ν . Если задано разбиение интервала ^ν нач

[ ν _нач , ν _кон ] точками:

P = ^{vJ i = 1.. N , ^v нач <  V <  ^v 2 < - <  ^v n <  ^v кон }, то вместо функций рассматриваются вектора с координатами x i = x ( ν i ) y i = y ( ν i ), для которых скалярное произведение рассчитывается по формуле:

N

( x , y )= ∑ x_iy_i . Для случая N =2 выражение (1) сов- i =1

падает с косинусом угла между векторами X и у .

Из определения SAM (1) следует, что при x ( ν ) ≡ y ( ν ), ∀ ν ∈ [ ν _нач , ν _кон ] ⇒ ρ =1. И для дискретного     случая:      x i ≡ y i , i =1.. N ⇒ ρ =1. Если

∃ν∈[νнач,νкон],т.ч.x(ν)≡y(ν)⇒ρ<1. Для дис- кретного случая аналогичное условие можно записать так: 3i(1 < i < N) т.ч. xi X y , ^ p < 1. Равенство SAM единице для идентичных спектров и неравенство для различающихся позволяет использовать эту величину для определения меры схожести или различия в задачах распознавания.

В случае, если в каждой точке разбиения P имеется малая погрешность измерения, то вместо строгого равенства для SAM имеем приближённое: p ~ 1, при этом погрешность в силу определения (1) может быть только в меньшую сторону.

Если регистрируемые спектры таковы, что с высокой долей вероятности можно считать различия между спектрами, обусловленные случайной погрешностью, много меньше, чем различия, обусловленные различной природой анализируемых веществ, то в этом случае ([6, 12]) можно использовать некотоой порог, при превышении которого спектры будут считаться идентичными. В общем случае определение этих порогов трудоёмкая и технически сложная задача.

Если искажения, вызванные погрешностью измерения спектра, велики, то значения SAM для идентичных веществ могут стать сопоставимыми с соответствующими значениями для неидентичных веществ. Повышением значения порогов можно избежать наличия ложных срабатываний так, чтобы сильно искажённый спектр не отождествлялся ни с одним из эталонных. В результате чувствительность обнаружения веществ прибором уменьшается.

Знание закона распределения SAM как случайной величины при воздействии случайных возмущений в спектре позволяет осуществлять распознавание с заданной оценочной достоверностью результатов.

Исследование измеренных спектров как векторов, координаты которых рассчитаны на некотором разбиении рабочего интервала частот P , требует наличия модели процесса формирования и преобразования погрешностей измерения спектра. Характерным для задач обнаружения малого количества вещества является использование светосильных спектральных приборов, таких как Фурье-спектрометры. В работе авторами рассматривается система, использующая статический Фурье-спектрометр видимого и ближнего ультрафиолетового диапазона [12]. Модель формирования и преобразования шума в спектре должна учитывать ошибки измерения регистрируемой интерферограммы и восстановления спектра.

Если интенсивность света измеряется в диапазоне [ z_Ha4 , z кон ] оптической разности хода лучей в интерферометре, то согласно [13] в каждой точке разбиения О = ^{ z^ i = 1.. К , : . <  z , <  z 2 < - <  ^z _K <  z kOH ^} интенсивности истинной интерферограммы ( I' ) и зарегистрированной интерферограммы ( I ) связаны через погрешность 5 I выражением:

I ( z^ = I ' ( Z i ) + 5 I ( z i ), i = 1.. K . (2)

При этом система случайных { 5 _s ( z i .)} величин подчиняется уравнениям:

M ( 5 I ( z i )) = 0, i = 1.. K , f d

M ( 5 i ( z i ) -5 i ( z j )) =

i ,

0,

если i = j . если i ^ j .

К зарегистрированному спектру применяется Фурье-преобразование, которое в общем случае задаётся

соотношением:

x ( v ) = ( 1 / 2 п ) J I ( z ) exp( - i v z ) d z .                   (5)

-да

Фурье-образ от (2) с учётом (3) и (4) в соответствии с [13] позволяет связать на сетке разбиения P истинный спектр x ' ( v i ), зарегистрированный спектр x ( v i ) и погрешность 5( v i ) выражением:

x ^{( v} i ) = x ' ( ^v , ) ^{+ 5}<уД                                 ⁽⁶⁾

При этом система случайных величин { 5 ( v i )}

имеет следующие моменты: M ( 5 ( v i ))= 0, i = 1.. N , M ( 5 ²( v i ))= g ², i = 1.. N .

В [13] приводится для используемой модели соотношение, связывающее ошибку в измеренной интерферограмме с ошибкой восстановленного спектра:

A B = h (2 N )^1/2 A I . (8)

Воспользуемся для описания ошибки спектра 5( v i ) в точках разбиения P моделью нормально распределённой случайной величины: 5 ( v i ) ~ N (0, g ²), i = 1.. N . При таком допущении зарегистрированный спектр x может рассматриваться как случайная N -мерная величина ( x ~ N ( x ' , 2 )) с распределением, задаваемым со-

отношением:

Р ⁽ x ) =

( 2 п ) ⁽ N ²⁾ | 2 |^1/2

- 1( x - x ' ) T 2^{- 1}( x - x ' ) e -

, x e R N .

Выясним, какой вид может иметь ковариационная матрица £ в выражении (9). Как видно из определения, SAM - это величина, инвариантная относительно перехода в новый ортогональный базис. В двумерном случае это означает сохранение углов при переходе в новую систему координат при преобразовании векторов. Известно [14], что с помощью таких преобразований можно квадратичную форму, стоящую в степени экспоненты в (9), свести к диагональному виду. В такой системе координат ковариационная матрица принимает диагональный вид: £ = Е- о², где Е - единичная диагональная матрица размера N х N . Тогда всюду ниже считается, что ковариационная матрица диагональная и величина дисперсии шума постоянна и равна о², если это не так, то указанная операция приводит её к требуемому виду.

Определим спектральную базу эталонных спектров следующим образом:

В = { bl i , j = 1.. M b i e R + ( V i , j p ( b i , b j ) < 1)}.

Пусть в (1) первая переменная пробегает значения эталонных спектров

⁽ Р в = P ^{( B} , ^x ) = ⁽ P ⁽ b_v x ), ^- , p ⁽ b_M , x )) T ), тогда получим новое отображение:

Р _в : R N ^ I [-.^ = [ - 1,1] х - -- х [ - 1,1] ,             (10)

M где i-я координата правой части равна SAM, рассчитанному для i-го эталонного спектра.

Исходя из предложенной модели, зарегистрированный спектр выражается через истинный по формуле (6). Пусть искомое вещество является одним из эталонных с номером ^, тогда выражение (6) примет вид: x = b , + 5 . Используя отображение (10), получим образ измеренного спектра в I _н 1] :

Р = Р _в ^{( x )} = ⁽ Р 1 ^, ^ ^, Р м ) T .

Требуется определить вектор-столбец математических ожиданий и ковариационную матрицу случайной величины р е R M по известной величине разброса ошибки спектра о² в предположении, что искомое вещество совпадает с одним из эталонных. Пусть это вещество в эталонной базе спектров под номером , , тогда задача состоит в определении вектора ц , _{м х 1} и матрицы А , _{м х м} , координаты которых определяются, исходя из следующих выражений:

O , _v = M ( P v ),                                   (11)

А^ = M (( P v - M ( P v )) ■ ( Р е — М ( Р е ))).          (12)

В приложении (см. п. 5) представлен подробный вывод аналитических выражений для этих коэффициентов. 1.2. Учёт характеристик нормированного скалярного произведения в задаче идентификации

Известно, что заданная ковариационная матрица X и квадратичная форма x^T X ¹ x задаёт метрику d_N ( x , y ) = ( x - y ) T X^{- 1}( x - y ) в R N . Если дан случайный вектор x , для которого известно распределение x ~ N ( b , , X = E ■ст ²), то по заданной вероятности P * можно указать расстояние d * такое, что выполняется условие: P ( d_N ( x , b , )> d * ) = P * . В связи с этим обстоятельством удобно ввести систему классов {W i }, соответствующих каждому эталонному веществу из базы спектров:

W , ={ a | а е R N , d_N ( a , b , )< d * }.                  (13)

Заметим, что чем выше вероятность P *, тем меньше расстояние d *.

По введённой выше системе { W i } задачи идентификации веществ может быть сведена к задаче определения принадлежности измеренного спектра одному или нескольким её элементам. Селективность методики идентификации веществ можно определить как минимальную величину P *, при которой выполнено условие: V i , j = 1.. M,W i n W j = 0 .

Вычислительная сложность задачи определения вероятностей по заданному распределению случайной величины в многомерном пространстве быстро увеличивается с ростом размерности. Предлагается использовать отображение (10) для перехода в про- странство меньшей размерности, равной числу эталонных спектров.

С учётом полученных выражений для ц и А случайный вектор р ( x ) е R M можно аппроксимировать нормально распределённой случайной величиной:

1         - З(р-ц) T А-1(р-ц)        „ p (Р) =----------e 2              , Ре RM .(14)

( 2 п ) ⁽ N ²⁾ | А |^1/2

На практике такое приближение является удовлетворительным для широкого интервала значений величины погрешностей в спектре.

Ковариационная матрица так же, как и в исходном пространстве спектров, задаёт в пространстве SAM метрику:

^d M ⁽ Р ^{( x} ), Р ⁽ У )) = ⁽ Р ^{( x} ) ^- Р ⁽ У )) T ^А ' ⁽ Р ^{( x} ) ^- Р ⁽ У )) .

По заданному распределению р и данной вероятности P * аналогичным образом можно определить расстояние d **, удовлетворяющее условию:

P(dM (Р(x), Ц, )> d ** ) = P*, с помощью которого определяется система классов {Wi}:

W , ={ a | d M ( р ( а ), ц , )< d ** ).                     (15)

Определение границ классов в этом случае требует интегрирования в M -мерном пространстве. Величина M равна количеству веществ в эталонной базе спектров, и их количество может быть велико. Удачным выбором системы координат в пространстве R^M сложность задачи интегрирования может быть уменьшена с M L до L • M , где L - количество точек разбиения для численного интегрирования вдоль одной оси. Такой системой координат будет ортогональная система собственных векторов матрицы А . Растяжением осей можно добиться приведения квадратичной формы ( р-ц_р ) T А ^{- 1}( р-ц_р ) к каноническому виду. Преобразование ФЛ^{- 12} приводит ковариационную матрицу к единичному виду. В новых осях функция распределения случайной величины р( x ) примет вид:

P ( Р ) =

.

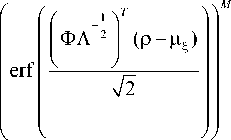
Основываясь на проделанных рассуждениях и полученных выражениях для ц , и А , , предлагается алгоритм идентификации веществ по спектрам, схема которого показана на рис. 1.

Если условие в цикле выполнено более одного раза, то выбирается вещество, для которого величина условной вероятности P ( a|a=b i + 8) максимальна. В роли порога срабатывания в данном случае выступает величина P *, по которой в предложенном алгоритме рассчитываются классы { W i }.

1=0

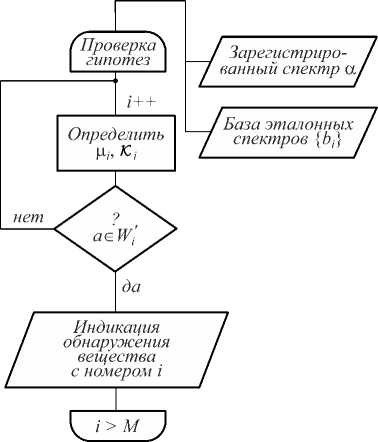
Рис. 1. Схема алгоритма идентификации веществ по спектрам люминесценции

В представленном методе расчёта меры схожести используется величина, которая имеет смысл вероятности. Это качественным образом отличает этот способ от прочих методов, в которых используется мера схожести. Для их применения требуется эмпирически определять пороги срабатывания для каждого эталонного вещества [15]. При этом добавление новых веществ в базу данных может приводить к ухудшению работы всей системы. Предложенный авторами новый способ идентификации веществ, основанный на проверке гипотез, потенциально лишён указанного недостатка. Это позволяет один раз задать порог срабатывания (вероятность ошибки) для всех эталонных элементов спектральной базы данных. При этом введение нового вещества не повлияет на надёжность работы системы в целом.

2.    Эксперимент

Использовались спектры, зарегистрированные статическим Фурье-спектрометром, который входил в состав макетного образца прибора, осуществляющего экспресс-анализ присутствия жидких и твёрдых веществ на различных подстилающих поверхностях [16]. Устройство позволяет обнаруживать твёрдые и жидкие вещества в форме остаточных следов на различных поверхностях. Для триптофана обнаружительная способность в зависимости от условий эксперимента может достигать значений до 1 мг на площади 1 м2. Схема установки показана на рис. 2.

Вторичное излучение, которое падает на объектив оптоволоконного зонда 1, собирается оптической системой линз и фокусируется на передний срез оптоволокна.

Оно подключено ко входному коллиматору спектрометра. В качестве подложки 3 использовалась специальная поверхность из непрозрачного не люми-несцирующего стекла. Его рабочий диапазон чувствительности равен интервалу длин волн от 320 нм до

750 нм, который содержит видимый свет и ближнюю ультрафиолетовую область.

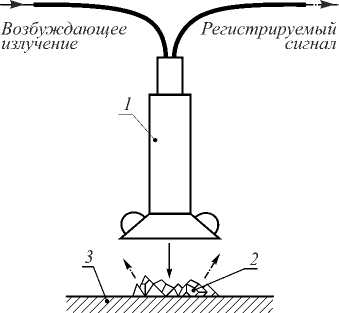
Рис. 2. Схема экспериментальной установки:

1 – оптоволоконный зонд, 2 – тестовое вещество, 3 – подложка

Прибор, помимо спектрометра, состоит из источника возбуждающего излучения и оптоволоконного световода с зондом на конце. Последнее устройство позволяет направлять и концентрировать возбуждающее излучение непосредственно на объект исследования и собирать как можно больше рассеянного излучения для анализа. В качестве источников возбуждающего излучения (см. рис. 2) использовались диоды с пиками излучения на длинах волн 280 и 310 нм, а также лазерный источник излучения с длиной волны 266 нм. В качестве тест-объектов 2 использовались вещества: антрацен, POPOP, PPO, стильбен и триптофан. Спектры этих веществ с указанием особенностей их химического строения показаны на рис. 3.

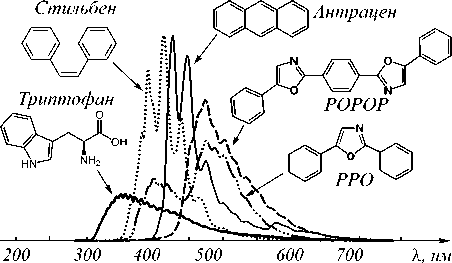
Рис. 3. Спектры люминесценции тестовых веществ, зарегистрированные с использованием источника возбуждающего излучения лазера, длина волны – 266 нм;

по оси ординат откладывается интенсивность в относительных единица

В дальнейшем для краткости эти вещества будут называться «тестовыми веществами». Рассмотренные тестовые вещества являются люминофорами при использовании данных источников подсвечивающего излучения. Как видно из рис. 2, спектры этих веществ в значительной степени перекрываются.

• 2.1.    Численный эксперимент

• 2.2.    Физический эксперимент

Для выявления возможных ошибок в расчётах, а также для проверки корректности сделанных упрощений при определении математического ожидания и ковариационной матрицы был проведён численный эксперимент с использованием псевдослучайных величин, соответствующих рассмотренной модели формирования интерферограмм и восстановления спектра. В частности, проверялась справедливость упрощения, в результате которого учитывались 17 из 36 коэффициентов матрицы (21).

На рис. 4 показано три графика зависимости математического ожидания SAM от среднеквадратической ошибки, рассчитанные для веществ POPOP и антрацен и для веществ PPO и антрацен, а также ковариации этих величин. При этом спектр антрацена состоял из эталонного спектра антрацена и аддитивно добавленной случайной ошибки, распределённой по нормальному закону. Величина среднеквадратического отклонения этой ошибки откладывалась по оси абсцисс графиков рис. 2.

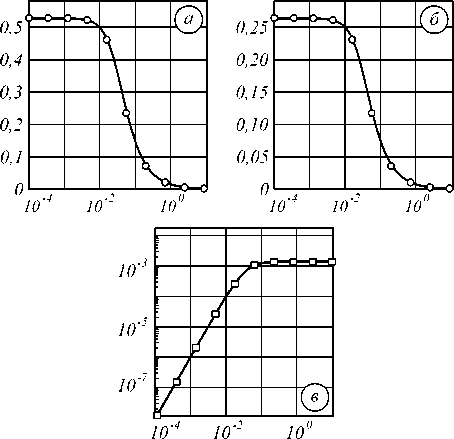
Рис. 4. Кривые зависимости математического ожидания величины нормированного скалярного произведения (ось ординат) от величины среднеквадратического отклонения шума в спектре (ось абсцисс); сплошная кривая рассчитана для веществ POPOP и антрацен (а) и для веществ PPO и антрацен (б); приведена кривая ковариации указанных величин (в); точками показаны значения, полученные при численном разыгрывании

Наблюдается совпадение теоретически рассчитанных кривых графиков и экспериментальных точек с точностью до ширины линий (см. рис. 2).

Известно, что нормально распределённая случайная величина является моделью, которая соответствует реальному объекту с различной степенью точности. Использование алгоритмов распознавания в реальных условиях эксперимента может привести к неудовлетворительным результатам, если параметры ошибок в регистрируемом спектре будут отличаться от предусмотренных моделью.

Апробация осуществлялась на примере более 4000 спектров, зарегистрированных в ходе экспериментов, которые повторяли условия применения прибора. Для каждого из тестовых веществ был зарегистрирован набор спектров, число которых варьировалось от 50

до 300. Величина сигнал/шум, которая рассчитыва- сигнал / P_шум , для всех спектров в наборе была постоянной. Изменение величины SNR осуществлялось с помощью выбора времени накопления сигнала на фоточувствительной матрице статического Фурье-спектрометра. Все прочие условия проведения эксперимента оставались постоянными для всех наборов и веществ.

По измеренным спектрам были рассчитаны статистические значения величины разброса SAM Для удовлетворительного согласия величины дисперсии с теоретически рассчитанной по формуле (23) потребовался пересчёт по формуле: I _ξ ^{( э )} = kI _ξ , где коэффициент k – неизвестный параметр, который был определён из условия минимального расхождения теоретических кривых и экспериментальных точек. Для спектров, зарегистрированных использованным статическим Фурье-спектрометром, этот параметр равнялся 2,1. На рис. 5 показано математическое ожидание и дисперсия SAM, рассчитанная для зарегистрированного спектра вещества стильбен и эталонного спектра этого же вещества.

• 2.3.    Апробация алгоритмов распознавания

Авторами в работе сопоставлялись два алгоритма распознавания. Первый, далее называемый «№1», предложен ранее в работах [6, 12]. В нём рассчитывалось значение меры схожести с эталонными спектрами, которое затем сравнивалось с пороговым значением. Превышение приводило к распознаванию соответствующего вещества в исследуемом образце. Второй алгоритм использует результаты, полученные в данной статье авторами, и изложен в разделе 1.2. Далее для краткости он будет называться «№2».

В табл. 1 приведены результаты для долей ложных срабатываний и верных срабатываний для спектров всех веществ, полученных от трёх источников возбуждающего излучения. Результаты представлены в виде дроби, где в числителе указана доля ложных срабатываний от общего числа возможных ошибок, а в знаменателе – соответствующая доля верных срабатываний. Верным считалось срабатывание, в результате которого обнаруживается только то вещество, которое служило источником регистрируемого прибором сигнала.

Таблица 1. Результаты распознавания в долях от максимального числа ошибок (числитель) и верных срабатываний (знаменатель)

Диапазон	Случай 1		Случай 2
	Алгоритм №1	Алгоритм №2	Алгоритм №1	Алгоритм №2
266	0,13/0,33	0,13/0,49	0,03/0,81	0,01/0,78
280	0,11/0,48	0,11/0,56	0,02/0,78	0,01/0,62
310	0,11/0,51	0,11/0,57	0,01/0,87	0,00/0,79

Если условиям алгоритма идентификации удовлетворило хотя бы одно лишнее вещество, то такое срабатывание считалось ложным и соответствующему счётчику присваивалось число таких (лишних) веществ.

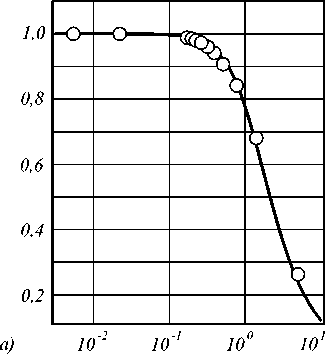
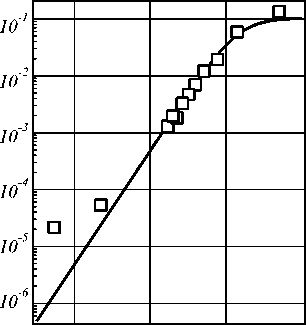
б)       10'2    10*     10° ю1

Рис. 5. Кривые зависимости математического ожидания (а) и дисперсии (б) нормированного скалярного произведения (ось ординат) от среднеквадратического отклонения ошибки экспериментального спектра (ось абсцисс); кривые рассчитаны при сопоставлении экспериментального спектра стильбена с его эталонным спектром; сплошная кривая рассчитана теоретически, маркерами отмечены результаты статистического анализа серии экспериментов

Результаты показаны для величин порогов, при которых число верных срабатываний максимально.

Из таблицы (столбец «случай 1») видно, что предложенный авторами алгоритм позволил распознавать больше веществ при одинаковом числе ошибок. Заметим, что в этих экспериментах отношение сиг-нал/шум варьировалось для различных веществ и находилось в интервале [1,01 - 1,05] .

Часто при работе приборов, предназначенных для автоматической идентификации веществ, в регистрируемом сигнале отсутствует полезная составляющая. Срабатывание в отсутствие полезного сигнала также считается ложным. Был определён порог срабатывания, при котором 98 % спектров, не содержащих полезного, не приводили к срабатыванию.

Результаты для такого случая показаны в таблице (столбец «случай 2»). Здесь использовались спектры с величиной отношения сигнал/шум в интервале [1, 04-1,19] . Из данных таблицы видно, что для «алгоритма №1» доля ложных срабатываний для боль- шей части экспериментов оказывалась больше, чем для «алгоритма №2». В то же время доля верных срабатываний для «алгоритма №1» оказалась больше. Т.е. «алгоритм №1» позволил распознать вещества в большей части случаев, в то время как «алгоритм №2» давал более надёжные результаты.

Выводы

Авторами рассмотрена одна из часто применяемых мер схожести, которая используется в задачах автоматического распознавания веществ по спектрам. Полученные выражения (22) и (23) позволяют определять параметры распределения меры схожести SAM в зависимости от величины среднеквадратического отклонения ошибок измерения в точках зарегистрированного спектра. Проведённый численный и физический эксперименты показали, что полученные соотношения можно использовать как применительно к модельному, нормально распределённому, так и применительно к реализуемому в эксперименте шуму. Для применения полученных формул к спектрам, регистрируемым в условиях эксперимента, потребовалось введение коэффициента k = 2,1, учитывающего отличия шума, реализуемого в спектрах от модельного.

Предложенный алгоритм идентификации веществ по их зарегистрированным спектрам люминесценции использует для анализа условную вероятность для проверки гипотез. Для сравнения рассмотрен существующий метод, в котором рассчитывается мера схожести по формуле SAM. Оказалось: если заведомо известно, что в анализируемом сигнале есть полезная составляющая, то предложенный алгоритм даёт выигрыш в доли верных срабатываний. Если в анализируемом спектре полезный сигнал может отсутствовать, то предложенный алгоритм позволяет добиться меньшего числа ошибок распознавания. Полученные в работе результаты могут быть использованы в методиках автоматического обнаружения веществ по их спектрам в таких задачах, как мониторинг окружающей среды и беспробоотборный химический анализ.

Приложение

Ниже приводится подробный вывод аналитических выражений для расчёта коэффициентов ковариационной матрицы и вектора математических ожиданий величин SAM, применённых для сопоставления эталонных спектров и одного экспериментального. При этом считается, что шум в зарегистрированном спектре аддитивный и стационарный.

В дальнейшем индексы, относящиеся к элементам эталонной базы спектров, обозначаются символами ξ, η и θ, а i , j , k , l , m и т.д. отвечают за координаты векторов. Подставив слагаемые x и b η в (1) и выразив величины ( x | b _η ), | x | и | b _η | через их координаты, получим:

N

B ξ ² η / B ηη + ( 1/ B ηη ) ⋅ ∑ δ i b η , i

ρ ξ , η = _N ^{i =} _N ¹       ,                   (17)

B ξ ² ξ + 2 ∑ b ξ , i δ i + ∑ δ i ²

i =1               i =1

NF                 N 2 §2 )

где B 8 = ^bib8 i . Заметим, что ^1 —у I подчиня-V “   '               “ l о J ется распределению %2. Как правило [12], количество точек в спектре велико и имеет порядок ~103 точек. Известно [13], что при N—ю распределение х2 под- чиняется нормальному закону, что позволяет записать приближённые выражения для его математического ожидания и дисперсии:

M | E § 2 I = N о ², D | £ § 2 I = 2 N о ⁴.         (18)

l i =1 J                  l i =1 J

Это позволяет записать выражения для некоторых слагаемых в (17):

N

^Sibn,i = an - N(0, о2B2n), iN=1                                                     (19)

£ § 2 = у - n ( N о ²,2 N о ⁴).

i =1

Линеаризация выражения (17) осуществляется стандартным образом. Для этого введём обозначение для подкоренного выражения знаменателя:

Y = B ^ + 2 a_s + y .

Его математическое ожидание с учётом (19):

ц Y = M ( Y ) = B ² ■ о ² N .

Что позволяет линеаризовать выражение 1 Y :

^JY ” ^Ц" -^l¹/ 2 ( ^{Y -Ц} Y ) .

Формула для определения нормированного ска- лярного произведения примет вид:

p n

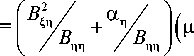
- 1/2

- 12 ц Y ^3/2 ( Y -ц Y ) ) .

У

Для упрощения введём коэффициенты:

An 1 = Bs2n Bnn A,2=1 B,n , A3 = 3 ц-1/2-1 2 Ц Y    2 -3/2 d2 ц Y  B ss , A4 = -цу3/2 , A,= - 2 ц Y1"- 2 F F1 0 0 FF4B28G2 0 F82 F02 B28C2 F2F3 B^ 0 IФ= 0 F84F, B2nC2 Fn3 F82B8° 0 F3 F Bk° 0 0 0 F85 FNо2 0 0 Fn5 F^^N+2)B28 l 0 Fn6Fg2( N + 2)B^ Fn6F3(N+2)B^      0 для математического ожидания:

^n = ^F n 1 + ^F n 4 ^B |, о ² + ^F n 5 ^N о ²

и для корреляции:

^ n8 j . i , j =1