Иерархическая модель процесса волочения проволоки в смещенных парах роликов

Современное развитие процессов волочения проволоки во многом связано с широким использованием роликовых волок. Волоки со смещенными парами роликов успешно конкурируют с монолитным инструментом при калибровке катанки и обработке труднодеформируемых материалов. Высокие требования, предъявляемые к качеству проволочной продукции, обуславливают необходимость точного определения размеров металла и силовых параметров процесса для широкого круга обрабатываемых материалов. Процессы волочения в смещенных парах роликов, предусматривающие деформацию металла по различным схемам, например, «круг-овал-круг», «гладкая бочка - гладкая бочка» характеризуются наличием, по крайней мере, одного размера поперечного сечения профиля, не контролируемого рабочим инструментом [1]. На величину и стабильность размера профиля, формирующейся в результате свободного уширения во второй паре роликов, оказывает влияние целый ряд факторов, учесть которые можно только с помощью математического моделирования.

Для описания напряженно-деформированного состояния металла в очаге деформации при волочении прямоугольной полосы в гладких роликах предложена математическая модель, базирующаяся на сочетании метода Ритца и метода конечных элементов [2]. В его основу положены зависимости, опубликованные в работах [2, 3]. При создании модели процесса непрерывного волочения в двух очагах деформации, в общем случае необходимо иметь несколько моделей, описывающих конкретные варианты процесса в каждом из очагов деформации, с точки зрения конфигурации калибровки роликов. Для решения оптимизационных задач и упрощения алгоритма путем создания единой модели деформации в обеих парах роликов, при описании модели процесса непрерывного волочения предложено использовать аффинные преобразования координат [3, 4], а в качестве обобщенной схемы деформации рассматривать схему «овал - овал». Данная схема позволяет варьированием величины радиуса калибра описывать требуемые схемы деформации (например, при больших значениях радиуса овального калибра - гладкая бочка, при одинаковых значениях радиуса овального калибра и его глубины - круглый калибр). Применение указанных выше приемов позволяет осуществлять оптимизацию расчета параметров процесса с точки зрения обеспечения тре буемого уширения металла, минимизируя целевую функцию F = (dx -dx)2, где d^ - заданный размер готового профиля; dx- фактический габаритный размер профиля по ширине. При этом имеет место задача математического программирования по минимизации функции ^(Х^при наличии ограничения X, ■ Х2 = ^т = const, где Xb Х2 , Xs - соответственно коэффициенты частной и суммарной вытяжки.

Известно, что при решении задач теории обработки металлов давлением, в частности для случаев деформации во вращающихся валках, формоизменение на участке свободного уширения и ряд других параметров, определяющих граничные условия, заранее не известны. Поэтому такие задачи решаются методами последовательных приближений, точность и быстродействие которых во многом зависят от качества первого приближения. Для улучшения сходимости алгоритма целесообразно использовать иерархический подход к моделированию [3], когда простые модели применяются с целью получения начальных приближений для более сложных моделей (рис. 1). Так, при анализе процесса волочения в волоках со смещенными парами роликов, для грубой оценки уширения и продольного усилия могут быть использованы эмпирические зависимости (I уровень модели), а для определения величины давления металла на ролики - выражения, полученные аналитическими методами (П уровень модели).

С целью получения эмпирических зависимостей проведено экспериментальное исследование процесса волочения круглого профиля по схеме «овал - круг». При планировании эксперимента использовался план полного факторного эксперимента ПФЭ 2³. В процессе эксперимента варьировались: диаметр заготовки - в диапазоне 6,0 ... 6,45 мм; диаметр роликов - в диапазоне 124 ... 172 мм. Величина противонатяжения, оцениваемая величиной относительного напряжения a₀/a_s. варьировалась в диапазоне 0 ... 0,14. Материал исходной заготовки - бронза кадмиевая БрКд 1,0. Для определения сопротивления пластической деформации обрабатываемого металла проведены дополнительные исследования с использованием кулачкового пластометра.

В результате статистической обработки экспериментальных данных получены следующие формулы.

Рис. 1. Схема построения модели процесса волочения в роликовой волоке

Ширина сечения после деформации

Л

Рс= —

-0,74

i_£l

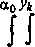
о О

где Ъ_о - ширина сечения до деформации; h₀ , h_x - высота сечения до и после деформации; R - радиус ролика по дну калибра; а₀ - напряжение про-тивонатяжения; ff_s0 - сопротивление металла пластической деформации перед рассматриваемым проходом.

Напряжение волочения

„5,053+1, 1511п4

с^а.бб^б^)1'94^-!)’   ’   л+о0.  (2)

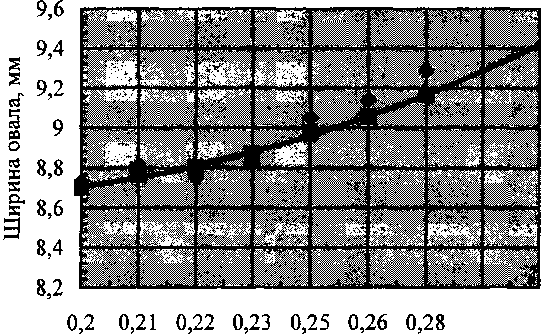
Сравнительный анализ полученных зависимостей показал хорошую сходимость последних с данными, полученными в проведенных ранее экспериментальных исследованиях для различных материалов (рис. 2, рис. 3).

Определение усилия, действующего на ролики со стороны обрабатываемого металла, выполняли аналитическим методом. Усилие на ролик соответственно составляет P = p_cS_k, где

^ = ^R6bxaQ - площадь контактной поверхности. Величина среднего контактного давления определялась выражением где

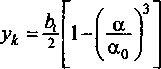
- горизонтальная проек ция границы контактной поверхности; а0- угол захвата по дну калибра.

В реальных условиях процесса волочения в роликовых волоках присутствуют различные возмущающие воздействия (нестабильность размеров, механических свойств металла, условий трения и т.п.), приводящие к колебаниям натяжения между парами роликов и, в конечном итоге, нестабильности геометрических размеров готового профиля.

Для качественной оценки влияния упомянутых факторов был выполнен вычислительный эксперимент с использованием разработанного программного продукта, в основу которого положены зависимости, опубликованные в работах [2, 5, 6]. При этом выяснилось, что характеристики элементов конструкции и условия трения в очагах деформации почти не влияют на колебания переднего натяжения на выходе из волоки. В то же время амплитуда колебаний натяжения между парами роликов зависит от соотношения жесткостей пар роликов и соотношения диаметров роликов первой и второй пары. Стабилизировать конечные размеры

Выдрин А.В., Баричко Б.В., Баричко Б.В.

Иерархическая модель процесса волочения проволоки в смещенных парах роликов

Обжатие

Рис. 2. Сравнительная оценка ширины овального сечения ■ - эмпирическая зависимость (1); ♦ - опытные данные, медь М1

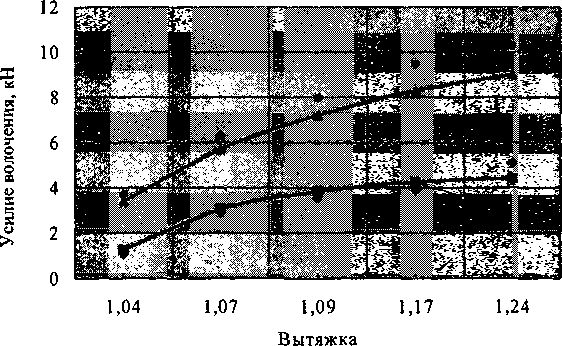
Рис. 3. Сравнительная оценка усилия волочения в первой паре роликов ■ - с использованием зависимости (2), медь М1; ♦ - опытные данные, медь М1; ▲ - с использованием зависимости (2), стальЮ; • - опытные данные, сталь 10

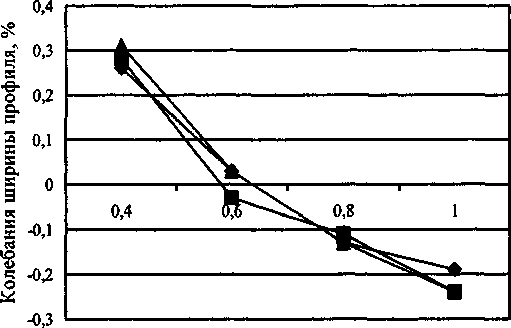
Соотношения коэффициентов жесткости пар роликов

—♦~fl/f2=l,0 -е-П/£2=1,3 -*-fl/f2=l,6

Рис. 4. Влияние жесткости пар роликов (Скх / Скг) на колебания ширины профиля профиля можно путем подбора соотношения коэффициентов жесткости первой (Cki) и второй (Ск2) пар роликов. Из графиков на рис. 4 видно, что при Сн/Си ”0,6 колебания размеров заготовки практически не оказывают влияния на колебания ширины готового профиля. При этом целесообразно стремиться к обеспечению одинаковых условий трения в обоих очагах деформации (т.е. при равенстве коэффициентов трения fi =f2\

В результате исследований получены эмпирические зависимости, которые использованы для определения начального приближения при реализации математической модели волочения в роликовой волоке со смещенными парами роликов.