Иерархическая система контроля доступа к информации на базе эллиптической криптографии с самоорганизацией

Современные сетевые технологии должны поддерживать передачу данных, звука, потокового видео. Поддержка требуемого качества услуги связи совместно с обеспечением информационной безопасности особенно проблематичны для беспроводных технологий. Последние заменяют кабельные сети благодаря эффективным способам формирования среды передачи для стационарных и мобильных вычислительных средств, на которых базируются качественно новые информационные услуги кооперации: автомобильные сети [1], тактические военные сети [2], платное цифровое телевидение [3], публичные сети городских парков, офисные локальные сети и другие мультимедиа приложения распределения данных в многоуровневом формате кодирования [4]. Безопасность подобных систем основана на механизмах шифрования данных, аутентификации пользователей и мониторинга сетевой активности, которые дополняются средствами адаптации системы контроля доступа под иерархическую структуру информационного взаимодействия.

Первые многоуровневые системы контроля доступа базировались на хэш-функции [7-9], которая позволяла быстро формировать группе-родителю ключи дочерних групп, но по групповым ключам получить ключ родителя невозможно. Данный принцип контроля доступа существует с 1983 г. [6], сохраняя характерные недостатки в современных модификациях:

• -    схемы не поддерживают реконфигурацию иерархии [10-11];

• -    схемы допускают использование иерархии определенной формы, например, направленный ациклический граф с одним корнем;

• -    сложно исключать пользователей в иерархии и, в общем, изменять число групп и пользователей в группе;

• -    контроль доступа производится главным сервером, безопасность которого является критической характеристикой всей системы.

Поэтому современные беспроводные сервисы имеют либо простейшую иерархию, либо жесткую структуру. Важно для гибких технологий иметь не менее гибкую систему безопасности. Для данной цели была разработана система контроля доступа на базе эллиптических кривых, удовлетворяющая требованиям стандарта ГОСТ Р 51241-2008 «Средства и системы контроля и управления доступом. Классификация. Общие технические требования. Методы испытания», но при этом исключающая необходимость наличия центра аутентификация. Разработанная система может функционировать с главным сервером, однако распределение его функций между пользователями повышает живучесть системы в целом.

Иерархическая система контроля доступа

Криптографические схемы на базе эллиптических кривых имеют преимущества в разрядности секретного ключа и скорости вычислений по сравнению с другими схемами [5]. Указанное преимущество является необходимым условием построения многоуровневой системы контроля доступа, поскольку обеспечение безопасного информационного обмена между уровнями и внутри уровня требует минимальных временных издержек на процедуры защиты данных. Причем пользователи группы более высокого уровня иерархии должны иметь возможность просматривать сообщения пользователей более низкого уровня. Многоуровневый контроль повышает бе- зопасность информационной системы и надежность.

Предлагаемая схема доступа обладает свойством самоорганизации, как и одноранговые сети ad hoc. Пользователи создают группу, формируя ключ их уровня иерархии и соответствующий их уровню доступа. Группа может быть допущена в иерархическую систему, если прошла аутентификацию у одной из родительских групп более высокой иерархии. Поэтому для создания системы достаточно существования одной группы, которой присваивается наивысший приоритет. Иерархия создается начиная с данной группы, реорганизуется. Группа может иметь различное число дочерних групп, находящихся на нижележащем уровне, и каждая группа может содержать несколько пользователей.

На каждом уровне создается список, содержащий родительские и дочерние группы. Каждая группа ассоциируется с эллиптической кривой Еp(a,b) вида y2 = (x3 + ax + b) mod p над Zp и генератором точек эллиптической кривой G = E(Zp), которые держатся в секрете от родительских, дочерних групп и групп одной иерархии.

Пользователи, каждый из которых вносит свой вклад, генерируют случайное число, соответствующее их группе. Разделяемый секретный ключ для каждой группы вычисляется независимо от изменения числа пользователей. Один пользователь в каждой группе наделяется правами главного члена группы. На том предположении, что пользователь, присоединившийся последним к группе, завершит сеанс позже остальных, можно принять, что главным членом группы становится последний присоединившийся пользователь. Главный пользователь каждой группы инициализирует процесс обновления группового ключа независимо от числа активных пользователей.

Таким образом, только активные пользователи на момент пролонгации системы безопасности будут иметь доступ к конфиденциальной информации. Если главный пользователь покидает группу, то пользователь, присоединившийся последним, становится главным. В этом случае групповой ключ обновляется для того, чтобы оставивший группу главный пользователь не смог получить доступ к конфиденциальным данным. Главный пользователь группы посылает групповой ключ всем главным пользователям групп, являющихся родительскими для данной группы. Сообщения нижележащей иерархии посылаются главному пользователю родительской группы, который расшифровывает сообщение, используя ключ дочерней группы, и зашифровывает, ис- пользуя ключ его группы. Затем распространяет зашифрованное сообщение между пользователями его группы.

Таким образом, каждый пользователь группы использует только ключ его группы, кроме главного пользователя, который хранит и применяет ключ его группы и дочерних групп. Данный способ эффективен, поскольку все изменения, связанные с группами любого уровня иерархии, остаются локальными для данных групп, и сообщения от дочерних групп получает только главный пользователь группы. На распределение пользователей и групп более высокой иерархии не оказывает влияние изменения числа пользователей и групп более низкой иерархии. Поэтому главный сервер можно исключить. Новая группа пользователей добавляется введением новой эллиптической кривой. Пользователи могут присоединяться и уходить из группы. Когда пользователь присоединяется к группе, он проходит аутентификацию и производится вычисление группового ключа. Когда пользователь покидает группу, производится генерация нового группового ключа. Таким образом сохраняется секретность при изменении числа пользователей.

Пример построения и эксплуатации системы контроля доступа

Рассмотрим численный пример для системы контроля доступа в случае пяти групп пользователей (см. рис. 1), каждой из которых соответствует эллиптическая кривая Еp(a,b) вида y2 = (x3 + ax + b) mod p:

• -    пусть группе А соответствует Е211(0, -4) с генератором G = (2, 2);

• -    пусть группе B соответствует Е337(8, -2) с генератором G = (0, 331);

• -    пусть группе C соответствует Е563(7, 5) с генератором G = (1, 442);

• -    пусть группе D соответствует Е823(5, -8) с генератором G = (3, 597);

• -    пусть группе Е соответствует Е127(3, 23) с генератором G = (5, 6).

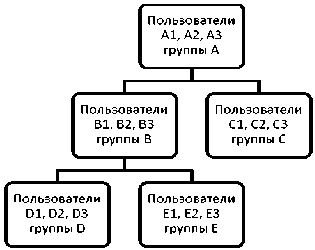
Рис. 1. Пример иерархической структуры доступа

Для иллюстрации функционирования системы контроля доступа рассмотрим первый этап формирования группы A, связанный с генерацией открытого и закрытого ключей первым членом группы А1. Секретный ключ пользователя А1 равный, например SА1 = 17, используется для вычисления открытого ключа для эллиптической кривой Е211(0, -4) с числом точек 240:

ОА1 = (SА1 mod p)×G = 17×G = (150, 85).

Предположим, что появился пользователь А2, который желает присоединиться к группе А со своим секретным ключом SA2 = 15 и открытым ключом

ОА2 = (SA2 mod p)×G = 15×G = (28, 2).

Тогда пользователям А1 и А2 необходимо сформировать их общий ключ. Для чего в соответствии со схемой Диффи-Хеллмана для эллиптических кривых А1, получив от А2 его открытый ключ (28, 2), вычисляет ключ группы А

КА = 17×(28, 2) = (201, 85).

Пользователь А2 на основании полученного от А1 ключа (150, 85) также вычисляет

КА = 15×(150, 85) = (201, 85).

Пользователь А2 становится главным.

Предположим, что пользователь А3 желает присоединиться к группе А со своим секретным ключом SA3 = 6 и открытым ключом

ОА3 = (SA3 mod p)×G = 6×G = (125, 152).

Для присоединения к группе необходимо вычислить новый общий ключ, причем главным пользователем группы становится А3. Для предотвращения передачи старого общего ключа по открытому каналу, с помощью которого можно дешифровать сообщения, перехваченные до присоединения А3, каждый пользователь обновляет свой секретный ключ и пересчитывает открытый ключ: SA1 = 91, OA1 = (206, 121), SA2 = 29, OA2 = (29, 139).

Тогда пользователь А3 вычисляет

SА3×ОA1 = 6×(206, 121) = (147, 97),

SА3×ОА2 = 6×(29, 139) = (131, 84)

и отправляет произведение SА3×ОА2 пользователю А1, а SА3×ОA1 – пользователю А2, когда бывший главный пользователь А2 отправляет пользователю А3 произведение SА2×ОА1 = (155, 115).

Тогда пользователь А1 вычисляет

КА = 91×(SА3×ОА2) = (120, 31), пользователь А2 вычисляет

КА = 29×(SА3×ОA1) = (120, 31), пользователь А3 вычисляет

КА = 6×(SA2×ОА1) = (120, 31).

Таким образом, сформирован новый общий ключ. Предположим, что пользователь А1 решил покинуть группу А, о чем сообщил всем ее чле- нам. Тогда каждый пользователь удаляет А1 из своих списков и новый главный пользователь обновляет свой секретный ключ и инициализирует вычисления нового группового ключа.

Пример процедур шифрования и дешифрования рассмотрим дляанглийскогословаМ= «free», используя однобайтовую кодировку ASCII. Для случайного ключа S = 202 зашифрованный текст имеет вид CipherTextМ = (S×G, PM + S×KA), где PM – символ передаваемого сообщения М, KA – групповой ключ, который для примера примем равным (198, 139).

При этом S×G = 202×G = (50, 57) используется для вычисления S при дешифровании. Тогда на стороне шифрования (например, А2) вычисляет S×KA = 202×(198, 139) = (27, 30) и

• -    для символа «f» 102×G = (114, 113), затем PM + S×KA = (114, 113) + (27, 30) = (104, 190);

• -    для символа «r» 114×G = (172, 50), затем PM + S×KA = (172, 50) + (27, 30) = (77, 145);

• -    для символа «e» 101×G = (1, 182), затем PM + S×KA = (1, 182) + (27, 30) = (156, 10);

• -    для символа «e» 101×G = (1, 182), затем PM + S×KA = (1, 182) + (27, 30) = (156, 10).

Таким образом формируется сообщение 50:5 7:104:190:77:145:156:10:156:10, которое на приемной стороне (например, пользователь А3) подвергается следующим преобразованиям.

• 1.    Из (50, 57) получаем значение S = 202 и вычисляем S×KA = (27, 30).

• 2.    Из первой точки эллиптической кривой шифротекста (104, 190) посредством вычитания находим (104, 190) – (27, 30) = (114, 113), что соответствует ASCII коду буквы «f».

• 3.    Из первой точки эллиптической кривой шифротекста (77, 145) посредством вычитания находим (77, 145) – (27, 30) = (172, 50), что соответствует ASCII коду буквы «r».

• 4.    Из первой точки эллиптической кривой шифротекста (156, 10) посредством вычитания находим (156, 10) – (27, 30) = (1, 182), что соответствует ASCII коду буквы «e».

• 5.    Из первой точки эллиптической кривой шифротекста (156, 10) посредством вычитания находим (156, 10) – (27, 30) = (1, 182), что соответствует ASCII коду буквы «e».

Таким образом, пользователи обмениваются информацией и обновляют групповой и секретные ключи.

Устойчивость системы безопасности к атакам различной реализации

Пользователь уровня с низкими привилегиями не может прочитать сообщения пользова- телей более высокой привилегии, поскольку в иерархической структуре нет передачи ключа от пользователей высокой привилегии к пользователям низкой привилегии. Если главный пользователь определенного уровня, имея несколько родительских групп на верхнем уровне, будет в сговоре с одним из родителей и получит ключ, то благодаря отсутствию связующего параметра между узлами родительской группы он не сможет сформировать ключ.

Также внешнему злоумышленнику неизвестны используемые эллиптическая кривая и генератор точки, что усложняет атаку. Совместная атака пользователей нескольких групп определенного уровня на родительскую группу невозможна, поскольку их ключи формируются посредством взаимодействия пользователей их групп. Даже если им удалось скомпрометировать одного пользователя вышележащей группы, узнав его ключ, они не смогут выдать себя за пользователя, контролирующего ключи, так же как и участвовать в формировании нового ключа. К тому же группы пользователей не могут получить ключ других групп того же уровня.

К необходимым рекомендациям можно отнести следующие. Родительские классы должны обновлять списки дочерних групп. Главный пользователь группы при изменении иерархии должен обновлять свои списки родительских групп. Обновление группового секретного ключа при изменении численности группы должно быть сделано посредством выбора случайного значения. Это необходимо для предотвращения случая, когда некоторые родительские группы по сговору желают заполучить ключ нижележащей и неподконтрольной группы.

От сговора родительских групп защищает передача только ключа и закрытие информации об эллиптической кривой и генераторе точек. Обмен ключами происходит в открытом виде, но без знания эллиптической кривой, имея даже переданное сообщение и ключ, невозможно осуществить дешифрование. Кроме того, изменяя генератор точек, можно на одной эллиптической кривой организовать различные схемы шифрования.

Заключение

Разработанная система контроля доступа основана на эллиптических кривых и имеет иерархическую структуру. Предложенная система может быть использована для доступа к информации, хранящейся на сервере, для безопасной передачи информации в сложной иерархической системе, а также для обеспечения безопасности обозначенных во введении качественно новых информационных услуг кооперации. Преимущества предложенной системы контроля доступа – возможность контроля за динамикой сообщений групп и отдельных пользователей, исключение необходимости использования главного сервера, небольшие аппаратурные затраты на реализацию.