Игра на «выживание» в квадрате
Автор: Ширяев Виктор Дмитриевич
Журнал: Инженерные технологии и системы @vestnik-mrsu
Рубрика: Теория игр, линейное программирование и приближенные методы анализа динамических систем
Статья в выпуске: 2, 2012 года.
Бесплатный доступ
В работе рассматривается игра преследования с «линией жизни» в квадрате S = = {(x; y)| - d
Короткий адрес: https://sciup.org/14719882
IDR: 14719882 | УДК: 519.832.4
Текст научной статьи Игра на «выживание» в квадрате
В работе рассматривается игра преследования с «линией жизни» в квадрате 5 = = { ( х ; у ) - d < х < d , - d < у < d ^ . Приводится решение игры в случае погонного преследования в предположении, что радиус встречи / = 0 (поточечная поимка) и игроки движутся с максимальными скоростями и и у.
Пусть на плоскости задано множество 5. Две точки — преследователь Р и преследуемый Е, обладая ограниченными по модулю линейными скоростями, перемещаются в множестве 5, имея при этом возможность в каждый момент времени изменять направление движения (простое движение). Преследуемый Е считается пойманным, как только расстояние между ним и преследователем Р достигнет значения, меньшего или равного I (/ > 0). Число / называется радиусом встречи. Целью игрока Р является поимка игрока Е до достижения последним «линии жизни» до момента /-встречи.
Приведем решение игры с «линией жизни» на полуплоскости в случае погонного преследования в предположении, что / = 0
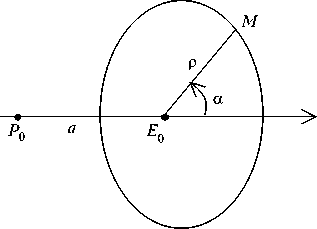
Рис. 1
(поточечная поимка) и игроки движутся с ( ^ ^
максимальными скоростями и и у I к = — I [1].
( о)
Если полярную ось направить по лучу Р о Е о , а за начало выбрать точку Е о (рис. 1), то полярные координаты р и а точки М улитки Паскаля удовлетворяют уравнению [2]:
р = 7— ( к + cos а ) . (1)
к2 - Г ’
Выберем теперь прямоугольную систему координат так, что прямая у о совпадает с «линией жизни». Пусть игрок Р имеет координаты (0; 0), а игрок Е — координаты ( х£ ;
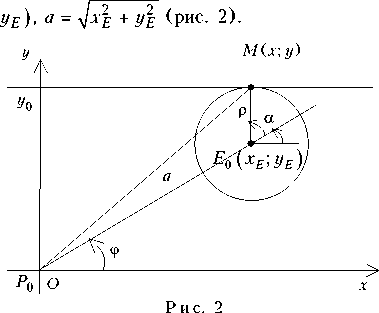
Вектор ОМ = ОЕ 0 + Е 0 М , ОЕ 0 = хЕ х х г + уЕ ■;.
Учитывая полярное уравнение (1) улитки Паскаля, можно выразить вектор Е о М :
Е ц М = р cos( ф + а ) ■ г + р sin( ф + а ) ■ j .
Таким образом, координаты точки встречи Р с Е имеют вид:
Решив данную систему, например по формулам Крамера, получим:
У о (к2 - 1)(к sin а + sin 2а)
( к3 cos а + 2к2 cos2 а + к cos а + sin2 а j
У о (к2 - 1)(к cos а + cos 2а) (4)
(к3 cos а + 2к2 cos2 а + к cos а + sin2 а)
х = Хр +— — (к + cos а) х
Е к2 -1
<
х (cos ф cos а -
У = У е +
а
к2 - 1
sin фsin а), (к + cos а) х
Учитывая, что -д/ 2 < а < л/ 2, проведем замены: sin а = t , cos а = 4 1 - t2 , - 1 < t < 1.
Таким образом, уравнения (4) принимают вид:
х (sin ф cos а + cos ф sin а).
У о (к2 - 1)Дк + 271 - t2 ) к(к2 + 1)71 - t2 + (1 - 2к2)^ + 2к2 ’
Подставляя значения хЕ = a cos ф, уЕ = a sin ф в(2), получим:
уо(к2 - 1)(к71 - t2 + 1 - 2t2) (5)
к(к2 + 1)71 - t2 + (1 - 2k2)t2 + 2к2
X = ХЕ I
Е к2
(
- ( к + cos а ) ( Х е cos а - У е sin а ) ,
.t е [ -1; 1.
У = У е +— 2--- ( к + cos а ) ( Х е sin а + У е cos а )
или — после соответствующих преобразований —
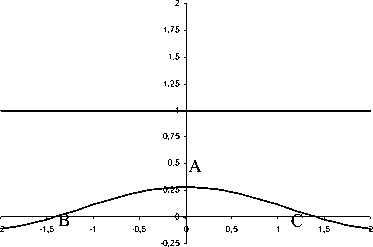
Уравнения (5) определяют границу выигрывающего множества игрока Е. Часть полуплоскости S, расположенная над линией (5), является выигрывающим множеством игрока Е. Вид границы выигрывающего множества при У о = 1, к = 2 приведен на рис. 3.
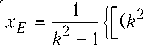
- 1) + cos2 а + к cos а I х
-
х х е - (sin а cos а + к sin и ) у е | , уЕ = рД^ {(sin а cos а + к sin а)хЕ + + |jk2 - 1 j + cos2 а + к cos а] У е^-
Уравнения (3) — уравнения улитки Паскаля при фиксированных Х е , У е , к.
Для того чтобы прямая у = у о была огибающей семейства улиток Паскаля, необходимо и достаточно, чтобы она в каждой своей точке касалась одной из улиток семейства. Для этого в точке встречи, кроме условия у = У о , добавляется условие касания у = О, так как касательный вектор параллелен оси Ох .
Таким образом, Х е , У е удовлетворяют системе уравнений
i
(sin а cos а + к sin а)х Е + |^ ( к2 - 1 ) + cos2 + к cos а] уЕ = у о ( к2 - 1 ) ,
( к cos а + cos 2а ) Х е - ( к sin а + sin 2а ) У е = 0.
Р и с. 3
Из уравнений (5) видно, что при изменении У о граница безопасности игрока Е подвергается преобразованию гомотетии с коэффициентом X = у о и ее характер, следовательно, сохраняется.
L к - 14
Вершина А имеет координаты [ 0,----I,
I к )
точки В и С пересечения с осью Ох получаются при значении cos a =
7к2 + 8 - к 4
Вид границы выигрывающего множества игрока Е при d = 3, к = 2 приведен на рис. 5.
Рассмотрим теперь случай, когда S является квадратом (5 = { (х; у) | -d < х < d, -d < у < d j ).
Как показано выше, в случае 5 = { (х; у) | -го < х < +го, 0 < у < d j граница зоны безопасности игрока Е определяется уравнением (4). Аналогично определяется граница выигрывающего множества игрока Е в случае 5 = { (х; у) | -го < х < +го, - d < у < 0 ^ :
i
d(k2 - 1)(k sin a + sin 2a)
Х е = 7—7----------7---7----------------7—Г ,
( к3 cos a + 2k2 cos2 a + к cos a + sin2 a )
_ d(k2 - 1)(k cos a + cos 2a) (6)
(k3 cos a + 2k2 cos2 a + к cos a + sin2 a)
■
Вид границы выигрывающего множества игрока Е при d = 1, к = 2 приведен на рис. 4.
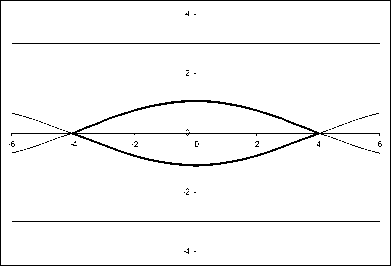
Р и с. 5
Рассмотрим теперь случай, когда «линией жизни» игрока Е является прямая х = d, т. е. 5 = { (х;у) | 0 < х < d, -го < у < +го ^ .
Выберем теперь прямоугольную систему координат так, что прямая х = d совпадает с «линией жизни». Пусть игрок Р также имеет координаты (0; 0), а игрок Е — координаты ( х е ; Уе ) - й = 7х Е + у Е (рис. 6).
0,5

-0,5
-1,5
Рис. 4

Р и с. 6
Объединяя оба рассмотренных случая в один, легко получить решение поставленной задачи в полосе -го < х < +го, - d < у < d ^ Граница выигрывающего множества игрока Е в этом случае определяется системой уравнений:
_ d(k2 - 1)t(k + 271 - t2 )
Е k(k2 + 1)71 - t2 + (1 - 2k2)t2 + 2k2 ’
‘ = + d(k2 - 1)(k71 - 12 + 1 - 2t2) (7)
" k(k2 + 1)71 - t2 + (1 - 2k2 )t2 + 2k2
t e [ -1; 1 ] ■
Для того чтобы прямая х = d была огибающей семейства улиток Паскаля, необходимо и достаточно, чтобы она в каждой своей точке касалась одной из улиток семейства. Для этого в точке встречи, кроме условия x = d, добавляется условие касания х = 0, так как касательный вектор параллелен оси Оу.
Таким образом, Х е , У е удовлетворяют системе уравнений:
[(k2 - 1) + cos2 a + k cos a)]x E - (sin a cos a + < + k sin a)y E = d ( k2 - 1 ) ,
( k sin a + sin 2a ) Х е + ( k cos a + cos 2a ) У е = 0^
Решив данную систему, например по формулам Крамера, получим:
d(k2 - 1)(к cos а + cos 2а)
^ к3 cos а + 2к2 cos2 а + к cos а + sin2 а )
‘ (8)
d(k2 - 1)(к sin а + sin 2а)
У е ч *
(к3 cos а + 2к2 cos2 а + к cos а + sin2 а)
Учитывая, что -я/2 < а < я/2, проведем замены: sin а = t , cos а = 71 - t2 , -1 < t < 1.
Таким образом, уравнения (8) принимают вид:
____ (10)
d(k2 - 1)t(k + 271 - t2 ) к(к2 + 1)71 - t2 + (1 - 2k2)t2 + 2к2
Вид границы выигрывающего множества при d = 1, к = 2 приведен на рис. 8.
-2
-1,5
= d(k2 - 1)(к71 - t2 + 1 - 2t2)
Е к(к2 - 1)71 - t2 + (1 - 2k2)t2 + 2к2 ,
= - d(k2 - 1)t(k + 271 - t2) (9)
к(к2 - 1)71 - t2 + (1 - 2k2)t2 + 2к2
_t 6 [ -1; 1 ] .
Уравнения (9) определяют границу выигрывающего множества игрока Е. Часть полуплоскости S, расположенная правее линии (9), является выигрывающим множеством игрока Е. Вид границы выигрывающего множества при d = 1, к = 2 приведен на рис. 7.
-2
-1,5
-1

1,5 2
Рис. 7
Аналогично определяется граница выигрывающего множества игрока Е в случае
5 = { (х; у) | -d < х < 0, - го < у < +го } :
< д£ = -
d(k2 - 1)(к71 - t2 + 1 - 2t2) к(к2 + 1)71 - t2 + (1 - 2k2)t2 + 2к2

0,5
1,5 2
Р и с. 8
Объединяя рассмотренные случаи в один, получим границу выигрывающего множества игрока Е в случае 5 = { (х; у) | -d < < х < d, -го < у < +го } :
хЕ
d(k2 - 1)(к71 - t2 + 1 - 2t2) к(к2 - 1)71 - t2 + (1 - 2k2)t2 + 2к2 ’
d(k2 - 1)t(k + 271 - t2 ) к(к2 + 1)71 - t2 + (1 - 2k2)t2 + 2к2
t 6 [-1; 1].
Вид границы выигрывающего множества при d = 1, к = 2 приведен на рис. 9.
-2
-1,5
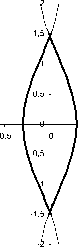
Рис. 9
1,5
Теперь легко получить решение игры на «выживание» в квадрате. Граница выигрывающего множества игрока Е в случае S = ^ (х; у) | -d < х < d, -d < у < d ^ получается как граница пересечения выигрывающих множеств игрока Е, определяемых системами (7) и (11). Вид этой границы при d = 3, к = 2,5 приведен на рис. 10.
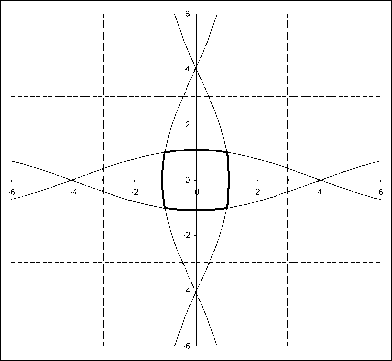
Список литературы Игра на «выживание» в квадрате
- Ширяев В. Д. Об одной задаче простого преследования/В. Д. Ширяев//Исследования по прикладной математике. Саранск, 1982. С. 22 25.
- Ширяев В. Д. Об одном способе определения улитки Паскаля/В. Д. Ширяев//Вестн. Ленингр. гос. ун-та. Сер.' математики, механики и астрономии. 1982. № 19. С. 107.


