KIRISH

Jahon miqyosida olib borilayotgan ko‘plab ilmiy-amaliy tadqiqotlar, aksariyat hollarda, metrologiya va okeanologiya sohalarida ko‘p fazali siqiluvchan muhitlar uchun dinamik jarayonlarni modellashtirish, shuningdek, mantiya jinslaridagi konvektiv massa almashinishi, filtratsion oqimlar va turli geologik jarayonlarning matematik modellari uchun sonli-analitik usullarni yaratish masalalariga keltiriladi. Fazalararo intensiv massa almashinuvi kuzatiladigan neft va gaz konlarini ishga tushirish va ulardan foydalanish jarayonida tabiiy qatlamlardagi flyuidlar oqimini hisoblashda ko‘p fazali muhitlar modelini yechish, matematik modellashtirish va hisoblash matematikasi sohalari bo‘yicha olib borilayotgan tadqiqotlarning obyekti hisoblanadi. Shu sababli, ikki tezlikli gidrodinamikada yuzaga keladigan bir o‘lchovli Byurgers tipidagi tenglamalar sistemasi uchun Koshi va chegaraviy masalalalarni sonli yechish sxemalari hamda algoritmlarni qurish, dasturiy vositalar majmuini yaratish amaliy matematikaning muhim vazifalaridan biri bo‘lib qolmoqda.

Ko‘p fazali oqimlarni modellashtirish va aralash elliptik-giperbolik tipdagi tenglamalar sistemasi uchun boshlang‘ich-chegaraviy masalalarni keng tadqiq etishda boshlang‘ich-chegaraviy shartlarning nokorrekt qo‘yilishi bilan bog‘liq bo‘lgan qiyinchiliklarni bartaraf etish uchun o‘zgarmas bosimli modelning turli giperbolik ko‘rinishdagi matematik modellarini tuzish va ularni sonli usullar yordamida yechishga qaratilgan ilmiy tadqiqotlar olib borilmoqda.

Ushbu yo‘nalishda, jumladan Byurgers tipidagi tenglamalar va ularning sistemasi orqali ifodalanuvchi modellar metrologiya, okeanologiya neft va gaz sohalarida keng qo‘llash bo‘yicha tadqiqotlar ustivor hisoblanmoqda. Shu bilan birga, o‘zgarmas bosimga ega bo‘lgan qo‘shsuyuqlikli muhitda nochiziqli to‘lqinlar tarqalishining matematik modelini takomillashtirish, ikki tezlikli gidrodinamikada yuzaga keladigan Byurgers tipidagi bir o‘lchovli tenglamalar sistemasi uchun Koshi masalasini yechish dolzarb vazifalardan hisoblanadi. [1:105], [8:153].

• 1.    Byurgers tipidagi tenglamalar sistemasi uchun Koshi masalasi.

Bir o‘lchamli holatda ushbu sistema quyidagi ko‘rinishga ega ди    ди     д~и .

--vu — = г\ —- -b—(u-v) + F dt    дх    дх ^

,        (1)

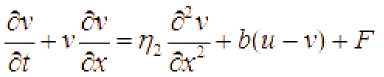
• (1)    va (2) formulalarda Ь -fazalararo ishqalanish koeffitsiyenti, g‘ovak muhitlar uchun Darsi koeffitsiyentining analogi hisoblanadi.

• 2.    Byurger tipidagi tenglamalar sistemasi uchun Koshi masalasini kuchsiz yaqinlashish usuli.

  (1), (2), (3) masalaning

  
  

  Koshi masalalariga to‘xtalamiz.

  
  

  Faraz

  
  

  qilaylik,

  
  
  
  
  

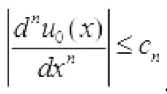
  ва

  
  
  

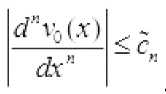
  I

  
  

  л = 0Д2

  
  
  
  

(1), (2) Byurgers tipidagi tenglamalar sistemasi uchun ta’sir etuvchi kuchlarni

1           1 Л zF(Г.X) = О X nrojl = {(Г,х): 0 < t < T,x g IR1} hisobga olmagan holda (          )                              sohada quyidagi boshlang‘ich shartlarga ega Koshi masalasini ko‘rib chiqamiz.

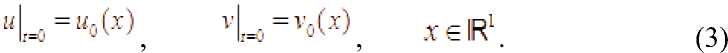
Bizni (1), (2) Byurgers tipidagi tenglamalar sistemasi uchun Koshi

. ШГ.Х).Т(Г.Х) G С12                                                   .

masalasining                      V 1 ■ xossalarga ega bo‘lgan yechimlari qiziqtiradi - bir marta ' bo‘yicha va ikki marta * bo‘yicha uzluksiz differensiallanuvchi funksialar sinfi. Kuchsiz approksimatsiya usuli bilan Byurgers tipidagi bir o‘lchovli tenglamalar sistemasi uchun Koshi masalasi yechimining mavjudligi va yagonaligi isbotlangan [2;39], [3:56].

bu yerda и,    - biror berilgan manfiy bo‘lmagan o‘zgarmaslar.

Avval, Koshi masalalari cheksiz differensiallanuvchi bo‘lgan holini ko‘rib

лЛаттитЫ u0(X)r\(x) eC=(IR- J chiqamiz. Faraz qilamizki,                       va

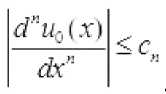
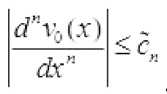
X e IR1

Kuchsiz approksimatsiya usuliga ko‘ra, (1), (2), (3) Koshi masalasini quyidagi masala bilan approksimatsiyalaymiz:

CW ,   .

—=-^l"„ or

3t

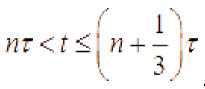
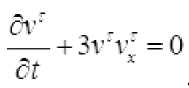
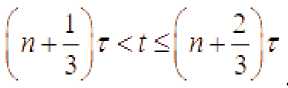
cl

--h 3uu: =0

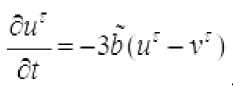
u'(O,x) = uQ(x)

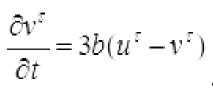
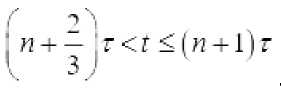
vr(O.x) = vo(x)

bu yerda

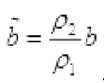
1 - butun

son,

va

Izoh 1.: (6)-(9) masala yechimini tuzishda birinchi kasr qadamlarda issiqlik o‘tkazuvchanlik tenglamasi uchun Koshi masalasi yechiladi, ikkinchi kasr qadamlarda - ko‘chish tenglamasi uchun Koshi masalasi, uchinchi kasr qadamlarda esa - oddiy differensial tenglamalar sistemasi uchun Koshi masalasi yechiladi.

Masalaning yechimi quyidagi ko‘rinishga ega

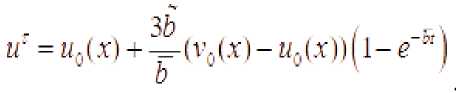
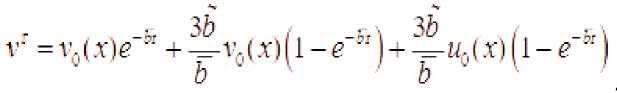
bu yerda b =3(b+b)

(5) munosabatlar bajarilgan bo‘lsin va shartlarni qanoatlantirsin

C1

C1

va

t

t

U xolda

soxada 1; va

yechim mavjud vа

г

bo‘yicha o‘zining barcha hosilalari

bilan chegaralangan.

* o‘zgaruvchilar

Aniqki, ixtiyoriy

fiksirlangan da (6)-(9) masalaning bo‘lmagan xolda chegaralangan.

1Г

va 1 yechimi

kattalikka bog‘liq

Yuqorida keltirilgan muloxazalarni

takrorlab, :i va

1 yechimlarning х

bo‘yicha ixtiyoriy tartibli xususiy xosilalari * bo‘yicha chegaralanganligini ko‘rsatish mumkin:

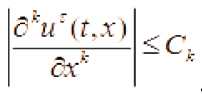
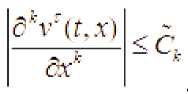
■j.

£ = 0. L....    (12)

bu yerda

biror musbat o‘zgarmaslar bo‘lib,

(11), (12) tengsizliklar va (6)-(9) tenglamalardan z bo‘yicha tekis baholashlar kelib chiqadi:

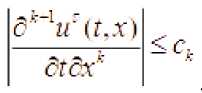
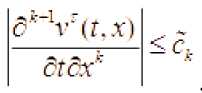
■j.

bO.L....   (13)

Bu baholashlardan ll

' va ularning ^ bo‘yicha ixtiyoriy tartibli hosilalari

da tekis chegaralangan va tekis darajada uzluksiz ekanligi kelib chiqadi.

Arsela teoremasiga asosan, diagonal usuli bilan fa } , {v}ketma-ketlikning sohaning xar bir chegaralangan qism soxasida o‘zining х bo‘yicha barcha xosilalari bilan mos ravishda ^ va 4 funksiyalarga tekis yaqinlashuvchi qism ketma ketliklarini tanlab olish mumkin, buning natijada 1; va v funksiyalar х bo‘yicha ixtiyoriy tartibli xosilaga ega bo‘ladi va quyidagi munosabatlar bajariladi

C H(t,X)

^ M LX)

-c* (Lx)en-.

£ = 0,1....

Yechimning yagonaligi standart usul bilan isbotlanadi.

Natijada, i; , funksiyalar ketma-ketliklarining o‘zi xam r^O da o‘zining barcha xosilalari bilan da mos ravishda “ va 1 ga tekis yaqinlashadi.

bo‘lgan xol o‘rtacha funksiyalar yordamida isbotlanadi.

Shunday qilib, quyidagi teorema isbotlangan.

Teorema 1. “oOXi’jO) - funksiyalar (3.3) shartni qanoatlantirsin. U holda (6)-

• (9) masalaning          va ^(л^) yechimi ^г?г sohada г^О da (1), (2), (3)

с ’ u(t, х) с^f >’(Л х)

masalaning «чл^ va -J yechimiga tekis yaqinlashadi. ст , St

, hosilalar п?< sohada а (Л VI va НДх) ning tegishli hosilalariga tekis yaqinlashadi.

Burgers tipidagi sistema qo‘shsuyuqlikli muhit modelining tenglamalar sistemasini soddalashtirilgan ko‘rinishi bo‘lib, bosim o‘zgarmasligi va siqilmaslik shartining yo‘qligi bilan qo‘shsuyuqlikli muhit modelining tenglamalar sistemasidan farq qiladi. Shu sababli, Burgers tipidagi sistema uchun masalalar to‘plami ba’zan o‘zgarmas bosimga ega bo‘lgan ikki tezlikli suyuqlik dinamikasi deb ataladi.

Ikki tezlikli gidrodinamikada yuzaga keladigan Burgers tipidagi tenglamalarning bir o‘lchovli sistema uchun Koshi masalasi ko‘rib chiqildi. Kuchsiz yaqinlashish usulidan foydalanib, Burgers tipidagi bir o‘lchovli sistema uchun Koshi masalasi yechimining mavjudligi va yagona ekanligi isbotlangan. Riman tipidagi tenglamalar sistemasining harakatlanuvchi to‘lqinlar ko‘rinishidagi yechimi ko‘rib chiqildi.[4:10], [5:20], [6:5], [7:153], [9:11].

Foydalanilgan adabiyotlar ro’yxati:

• [1]    Турдиев У. К., Кодиров Ф. Э. Задача Коши Для Одномерной Системы Уравнений Типа Бюргерса Возникающей В Двухскоростной Гидродинамике //Инновации в технологиях и образовании: сб. ст. участников XI Между. – 2018. – С. 349.

• [2]    Turdiyev U., Imomnazarov K. A system of equations of the two-velocity hydrodynamics without pressure //AIP Conference Proceedings. – AIP Publishing, 2021. – Т. 2365. – №.1.

• [3]    Турдиев У. К. Система уравнений типа Римана, возникающая в двухжидкостной среде: Система уравнений типа Римана, возникающая в двухжидкостной среде //MODERN PROBLEMS AND PROSPECTS OF APPLIED MATHEMATICS. – 2024. – Т. 1. – №. 01.

• [4]    Turdiev U. K., Kh I. K. Riemann-type system of equations arising in a two-fluid medium //Abstr. Int. Conf. Inverse and Ill-Posed Problems (Oct. 2–4, 2019, Samarkand, Uzbekistan). – 2019. – С. 119-120.

• [5]    Turdiev U. K. Imomnazarov Kh. Kh. A system of equations of the Riemann type arising in a two-fluid medium //Int. Conf.“Inverse and ill-posed problems. – 2019. – С. 119-120.

• [6]    Имомназаров Х., Турдиев У. К. Исследование задачи Коши для одномерной системы уравнений типа Бюргерса методом слабой аппроксимации //Проблемы информатики. – 2019. – №. 3 (44). – С. 20-30.

• [7]    Турдиев У. РЕШЕНИЕ И МОДЕЛИРОВАНИЕ ЗАДАЧИ КОШИ //International Scientific and Practical Conference on Algorithms and Current Problems of Programming. – 2023. – Т. 1. – №. 01..

• [8]    Имомназаров Б. Х., Турдиев У. К., Имомназаров Х. Х. Задача Коши для одномерной системы типа Бюргерса //Дифференциальные уравнения и математическое моделирование. – 2019. – С. 30-30.

• [9]    Имомназаров Б. Х., Турдиев У. К., Коробов П. В. ЗАДАЧА КОШИ ДЛЯ СИСТЕМЫ УРАВНЕНИЙ ТИПА БЮРГЕРСА //Математическое и компьютерное моделирование естественно-научных и социальных проблем. – 2019. – С. 9-14.

• [10]    Имомназаров Х. Х., Турдиев У. К. ОБ ОДНОЙ НАЧАЛЬНОКРАЕВОЙ ЗАДАЧИ ДЛЯ ОДНОМЕРНОЙ СИСТЕМЫ ПОРОУПРУГОСТИ //МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ УЗБЕКИСТАНА имени МИРЗО УЛУГБЕКА. – 2012. – Т. 204. – С. 48.

• [11]    Турдиев У. К., Имомназаров Х. Х. НЕКОТОРЫЕ ИНТЕРЕСНЫЕ КЛАССЫ СИСТЕМ УРАВНЕНИЙ ВОЗНИКАЮЩИХ В ДВУХФАЗНОЙ СРЕДЕ //КАРШИ ДАВЛАТ УНИВЕРСИТЕТИ. – С. 184.

• [12]    Qayumova G. THE ROLE OF INFORMATION TECHNOLOGIES IN THE DEVELOPMENT OF COMPETENCES OF INDEPENDENT WORK IN THE DIGITAL ENVIRONMENT //Science and Innovation. – 2022. – Т. 1. – №. 8. – С. 505-508.

• [13]    Raxmonov B. STUDENTS IN INTERDISCIPLINARY COMMUNICATIONS IN THE DEVELOPMENT OF INFORMATION COMPETENCE POSSIBILITIES OF IT-TECHNOLOGIES //Science and Innovation. – 2022. – Т. 1. – №. 8. – С. 509-514.

• [14]    Kalandarovich, Movlonov Ma’ruf. "THE ROLE OF SCIENCE BLOCKS IN TEACHING FUTURE ENGINEERS TO SOLVE ISSUES RELATED TO MANUFACTURING PRACTICE." Academia Repository 4.11 (2023): 119-122.

• [15]    Movlonov, M. K. "ZAMONAVIY AXBOROT TEXNOLOGIYALARIDAN FOYDALANISH ORQALI MATEMATIK FANI ELEMENTLARINI O ‘RGANISH." Экономика и социум 11-2 (126) (2024): 308311.

ФОРУМ МОЛОДЫХ УЧЕНЫХ №2(102) 2025