Ikkinchi tartibli Gronuoll chegaralanishli boshqaruvlar uchun tutish masalasi

R" fazoda P va E obyektlar berilgan va ularning harakatlari quyidagi differensial tenglamalarga asoslangan

P : x = u , x(O)-Ax(O) = О, |w(/)f - Р ^ 2/j |w(s)|² ds ,         (1)

о

E : У^^ , ’(oH^oM , |v(/)|²< cr² + 2/j |v(5)|² ds ,         (2)

о bu yerda ■^ – P obyektning R" fazodagi holati, *о=У°) , хл = x(O)–uning mos ravishda f = О vaqtdagi boshlang‘ich holati va boshlang‘ich tezligi; и quvlovchining boshqariladigan tezlanishi bo‘lib и : [O,oo) ^ R va u vaqt bo‘yicha o‘lchanuvchi funksiya sifatida tanlanadi; barcha

\u(t)^ < p2 + 2/j |w(s)f ds shartni qanoatlantiruvchi bunday ^ () o‘lchanuvchi о funksiyalar to’plamini Gp bilan belgilaymiz. У –E   obyektning R" fazodagi holati, y, =X°), л =Я°)   – uning   mos ravishda barcha

|v(O|² ^ f² + 2/j|v(^)|² ds о

shartni qanoatlantiruvchi bunday v(-) o‘lchanuvchi funksiyalar to‘plamini ^E bilan belgilaymiz.

Ta’rif 1. Agar (*O> ^P ^WC)), »(')eG„ uchlik berilgan bo’lsa, (1)

tenglamaning quyidagi yechimiga quvlovchining harakat trayektoriyasi deyiladi

/ s

x(t) = x0 +tx{ + ^n(r)dTds о 0

Ta’rif 2. Agar U, л^С)), ^v(-)^gGe uchlik berilgan bo‘lsa (2)

tenglamaning quyidagi yechimiga qochuvchining harakat trayektoriyasi deyiladi

J (/) = y₀ + ty_x + jjv(7-)drds о 0

Ta’rif 3. (1)-(2) masala uchun tutish masalasi ([1]-[2]) yechilgan deyiladi, agar qochuvchining ixtiyoriy ^v(-)^eG_£ boshqaruv funksiyasi uchun quvlovchining shunday " (')^eG„ boshqaruv funksiya mavjud bo‘lsaki, biror chekli t vaqtda quyidagi tenglik bajarilsin

0 = 0

Ta’rif 4 . (1) – (2) masala uchun quvlovchining П-strategiyasi ([3]-[4]) deb quyidagi funksiyaga aytamiz,

(v) = v-2(v)£

bunda ^ H, О00+7(о)2+^2/', 3 = p2-a2>0, (O) –v va ^0 vektorlarning R" fazodagi skalyar ko’paytmasi.

Teorema. Agar Granoull chegaralanishli ikkinchi tartibli differensial o‘yin (1)(2) uchun quyidagi shart p>a o‘rinli bo‘lsa, u holda П-strategiya (4) yordamida tutish masalasi (0,t) yechiladi va obyektlar orasidagi yaqinlashish funksiyasi quyidagicha bo‘ladi

Р~с h , P~a , P-^

/(/,/,|z0|,p,(7,^ = |z0|(^ + l)

Isboti. Faraz qilamiz, agar qochuvchi ixtiyoriy v(PGe bo‘lganda quvlovchi esa (4) ko‘rinishdagi strategiyani tanlasin, u holda (1) va (2) tenglamalarga asosan quyidagi Karateodori tenglamasini topamiz

z = -A(v{t^^

z(O)-b(O) = O,

Bundan boshlang’ich shartlarni berilishi bo’yicha quyidagi yechim aniqlanadi t s

--(/)=--t(tr+i)-f0 П4'(ги^drds о 0

yoki t                                      /--------------------------------------------

|z W| = lzo | (^ +4 "П^’^0) + V(v’ ^o )2 + ^^ )^5 о 0

Lemmaga ko’ra quyidagi tengsizliklarni hosil qilamiz t s

|^(0| - \~0\(kt + 1)-^e’\p - a^d-rds => о о

I             P         P

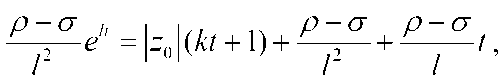
oxirgi tenglikni soddalashtirish orqali quyidagi tenglikni hosil qilamiz

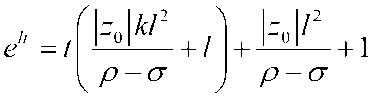
bunda л = ^^^/ , £ = ^l+] bo‘lib, bu yerda p>ct, B>\. Natijada p-а     p-a quyidagi tenglikka ega bo‘lamiz

e1' =At + B         (5)

Tutish vaqtini aniqlash uchun (5) tenglamani quyidagi hollarini ko‘rib chiqamiz.

ъ a~ P

• 1.    A <0 к         bo‘lsin. U holda (5) tenglama yagona t > 0 musbat

• 2.    ^{л=0        к}~~й/ bo‘lsin. U holda (5) tenglama yechimi

• 3.    ^>⁰^           bo‘lsin. U holda (5) tenglama t > о musbat yechimi

yechim mavjud va bu yechim tutish vaqti bo‘ladi. (1-chizma)

*      р-^ bo‘lib, tutish vaqtini beradi.

t -—-------- а-р                     *

mavjud va bu yechim tutish vaqti bo‘ladi.

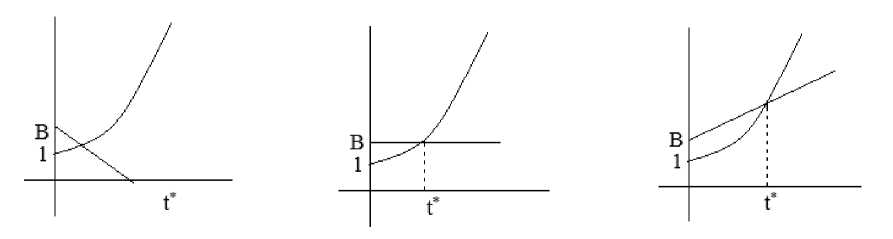
(1-chizma)               (2-chizma)               (3-chizma)

Foydalanilgan adabiyotlar

• 1.    Isaacs R. Differential games. John Wiley and Sons, New York, 1965 .

• 2.    Nahin P.J. Chases and Escapes: The Mathematics of Pursuit and Evasion. Princeton University Press, Princeton, 2012 .

• 3.    Azamov A.A., Samatov B.T. The П-Strategy: Analogies and Applications. The Fourth International Conference Game Theory and Management , St. Petersburg, Russia: 2010, p. 33-47.

• 4.    Samatov B.T. The Pursuit- Evasion Problem under Integral-Geometric constraints on Pursuer controls. Automation and Remote Control, Pleiades Publishing, Ltd. New York: 2013, 74(7), p. 1072-1081.

"Мировая наука" №6 (87) 2024