Image Comparison with Different Filter Banks On Improved PCSM Code

Published Online December 2016 in MECS

Digital image compression is commodious when a digital image has to store for future reference and transmit form one location to another for digital communication. Digitization of digital images provided a useful tool to the scholars of medical field, space engineering, defence enforcement and law area. Now with new technology in the field of digital image processing, we are creating a world where digital images become a very important part of our day by day life. The use of digital image compression is concern already in the abstract and also it is discussed that, by how many compression methods we can get the goal. Here, introduction and importance of the work is given in brief. In this work a digital image is converted into a frequency domain of the high spectrum and low coefficient spectrum and wavelet Parameters are ready to measure the performance of the specific coding technique [1]. In this paper an image is compressed by improved Progressive Coefficients Significance Method (IPCSM) and after compressing the code different filter banks apply on it to improve the quality of image. Image compression is a technique by which an image can be minimizing in size without losing the quality of original image. Image compression solved the problem of limitations of store the digital image. Digital Image Compression is use to reduce redundancy of the digital image code, the storage requirement, transmission time and process duration. A compressed image takes less memory space to store which indicates less time to need for processing of image. Wavelet image compression is very much popular because of its blocking artifacts nature and high quality multi-resolution reconstructed images quality. Many classy and novel wavelet based algorithm for image compression have been evolved and implemented in last few years. There are two types of digital image compression algorithms, Lossy image compression and Lossless image compression. In the Lossy image compression the compressed image is not replica as the input image. There is always some loss in output image [2]. Wavelet image compression, vector quantization and transformation coding are Lossy image compression. While in Lossless image compression the compressed output image is same as the original input image, there is no loss in original image quality. Huffman Encoding, Run length encoding and Incremental Encoding are Lossless image compression [3]. PCSM method helps to compress the digital image into a small code (bit rate) by which storing and transmission of a digital image one location to another and different filters are use improve the image quality. By this PCSM method, digital image is converted into frequency domain of the high spectrum and low spectrum of coefficient. These coefficients are converted by an appropriate method by which the digital image converted into small code of an array [4]. Reconstruct of the image by a decoder and after applying inverse image transform a reconstructed digital image which is almost replica of the input digital image [5]. There are some compression parameters to analyze the performance of reconstructed image. These parameters are mean square error (MSE), peak to signal noise ratio (PSNR), compression ratio (CR), execution time (ET), bits per pixel (BPP), root mean square error (MSE).etc.

The objective of this paper is not only provide the better compression method for real digital images but also provide a better quality of digital images by wavelet method. Here, an improved PCSM code used to compress the image into a lower bit rate code which further can be used for storing and transmission purpose. Wavelet transform is used as a basic tool to compress image followed with an encoding method to code the image pixels. This improved code will be calibrated with different filter banks of wavelet. For this purpose few important changes on the existing techniques we can achieve the best image compression result.

• II.    Related Work

This section provides a survey of the related work in the areas of classification for image compression. Many different approaches have been developed for classification of image compression over the past seven decades. Various applications are used in these researches.

In Ref. [1] a wavelet-based progressive image transmission method is proposed. Here also a combined method is proposed to minimize the image browsing time. The proposed scheme transforms a digital image from spatial domain into frequency domain by using discrete wavelet transformation (DWT) methods. For wavelet transformation phase they used Haar wavelet transformation. In Ref. [2] they introduced a great application in transferring videos and images over the web to minimize data transfer time and resource consumption. A lot of methods based on DCT and DWT have been introduced in the past like JPEG, MPEG, EZW, SPIHT etc. In Ref. [3] proposed a Wavelet-MFOCPN based technique and algorithm tested on varieties of benchmark images for color image compression. In Ref. [4] Defined the image compression is to minimize irrelevance image data in order to store the image in less memory and to improve the transfer time. In Ref. [5]

proposed image compression system not only good quality compressed images but also good compression ratio, while maintaining small time cost. In Ref. [6] prescribed the Image compression is the application of Data compression on digital images. Different techniques for image compression have been reviewed and presented that include DFT, FFT, DCT and DWT. In Ref. [7] described a novel method in image compression with different algorithms by using the transform of wavelet accompanied by neural network. In Ref. [8] reviewed lossless data compression methodologies and compares their performance. The refreshers have find out that arithmetic encoding methodology is very powerful over Huffman encoding methodology. In Ref. [9] presented a survey of various types of lossy and lossless image compression techniques and analysis it. In Ref. [10] examined the performance of a set of lossless data compression algorithm, on different form of text data. A set of selected algorithms are implemented to evaluate the performance in compressing text data. In Ref. [11] proposed for encryption and compression. This paper focuses mainly on highly secure encryption and high compression rate using SPIHT method in Larger Images. In Ref. [12] proposed two technique Lossy compression techniques and lossless compression. Lossless technique the image can be reconstructed without loss of information. But in lossy compression it cause some form of information loss when it reconstructed. In Ref. [13] digital image compression which uses the unique embedded Wavelet based image coding in combination with Huffman-encoder for more compression. In [14] they proposed a lossless image compression technique combining a unique step with the integer wavelet transform. The unique step proposed in this technique is a simplified version of the median edge detector algorithm. In [15] proposed a digital image compression used hybrid wavelet transform matrix. Hybrid wavelet transform is formed using some orthogonal component transforms. In [16] proposed some unique approaches to the rationalization of FDWT and IDWT basic operations execution with the reduced number of multiplications are considered. In Ref. [17] proposed a unique technique for lossless image compression. In Ref. [18] introduced a digital wavelet transform (DWT) based image compression methods have higher compression rate with less amount of memory requirements and execute image compression technique. By using of unique wavelet filters, dmey, Symlets, Daubechies, Coiflets, reverse bi-orthogonal and examine the compression performance. In Ref. [19] compared five different Wavelet based digital image compression techniques are analyzed. These techniques involved in the digital image comparison process. In Ref. [20] introduced a improved PCSM code, by reducing the execution time, increased PSNR and enhanced the compression ratio. Improved PCSM introduced a vital aspect in digital image compression and enhanced coding.

• III.    Background

• A.    Discrete Wavelet Transform (DWT)

For short-term Fourier transform, sine or cosine wave replaced by a short wave which was not long lasting wave. This short wave is wavelet and its transform is called as wavelet transform. Wavelet series in continuous domain is given as the combination of continuous scaling and wavelet function. The resulting coefficients in Discrete Wavelet Series expansions are called Discrete Wavelet Transform (DWT).Using DWT in image compression because of Discrete Cosine Transform (DCT) has a lot of major drawbacks. DCT is a cosine wave based image compression technique and it calculates the coefficients of frequencies by applying transform function to image or a region of image. In the region, DCT is completely unable to detect high or low frequency and just give the result of an averaging filter. Applying DCT in an image block by block creates reasonable compression artefacts i.e. blocking artefacts and also known as checker board effect in DCT [6]. To resolve the band limitation problem of DCT we have to use a short-term DWT instead of sine or cosine wave based transform in which it goes for the complete range of the signal. This short wave is known as wavelet and wavelet based transform is known as wavelet transform [7]. The scaling functions give low frequency analysis of signals to obtain approximations and wavelet functions provide high-frequency analysis of signals to extract details in signals. Here, a unique approach is presented in the direction of sub band analysis and synthesis and it will be shown how DWT would completely fit into the sub band coding and decoding requirements. DWT is widely used to perform the sub band analysis of signal in multi resolution approach. DWT and sub band decomposition have a good relationship and it is possible to compute DWT through sub band decomposition in sequences [8].

• B.    Progressive Coefficients Significance Methods (PCSM)

Progressive Coefficients Significance Methods (PCSM) used to compress the image into a lower bit rate code which further can be used for storing and transmission purpose. PCSM codes mainly contains the codes which includes Embedded Zero Tree (EZW) coding, SPIHT (Set Partitioning in Hierarchical Tree), ASWDR (Adaptively Scanned Wavelet Difference Reduction) WDR (Wavelet Difference Reduction) and STW (Spatial orientation Tree Wavelet) [9]. All these encoding methods process the compressing algorithm in progressive manner this means after each pass we will get a better version on compressed image.

• C.    Previous Modification on PCSM Code

An improved Progressive Coefficients Significance Methods (IPCSM) coding is presented which is an advancement and modification in SPIHT (Set Partitioning in Hierarchical Tree) and SWT (Spatial orientation Tree Wavelet) encoding of PCSM codes. This modified improved code use the list of SPIHT to perform the coding shorting in encoder and a tree based algorithm use to advance the compression process in the Progressive Coefficients Significance Methods (PCSM) series code. This improved code will contain the merits of both the coding of SPIHT and STW coding and improve the value of PSNR and MSE image compression parameters. Wavelet structure is applied on the image and combined with Discrete Wavelet Transform (DWT) and Progressive Coefficients Significance Methods (PCSM) algorithms performed one by one on the DWT coefficients [20].

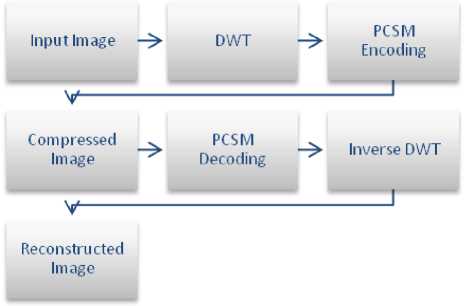
Fig.1. Planning Chart of Improved PCSM Code [20]

• D.    Filter Banks

All filter banks have some specific functions (mathematical functions). These mathematical functions work accordingly their specific purposes and help to change digital image in wavelet transform. Every filter bank has a wavelet functions and a scaling function. These filters are divided into two categories. Bi-orthogonal wavelet and Orthogonal functions [18].

• IV.    Proposed Algorithm

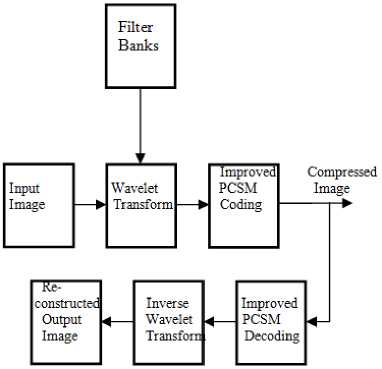
Fig.2. Block diagram of compression and reconstruction of a digital image

In this approach of image compression method first change the digital image from spatial domain to frequency domain by DWT method. In second stage coefficients of these frequency components quantized by using and appropriate encoding algorithms. Here an idea is, not all the components carry sufficient energy so lower energy coefficients can be suppressed and most of the information maintained by keeping high frequency components secure. After compressing the code different filter banks apply on it to improve the quality of image. Now for reconstruction of the same image a decoder is used to decode it into a function of frequency. After applying final step of using inverse transform a reconstructed image is taken back which is almost similar to the input image. In this paper these filters are demonstrated to show the performance of compression using wavelet functions. The new filter used some properties of basic wavelet filter. There is slightly change in the scaling function and wavelet function of these existing filters. Scaling and wavelet impulse response of proposed filter is given as:

Table.1 Scaling and wavelet function of proposed wavelet filter

Scaling Function	Wavelet Function
-0.0102009221870400	0.00134974786501000
-0.0102300708193700	-0.00135360470301000
0.0556648607799600	-0.0120141966670800
0.0285444717151500	0.00843901203981000
-0.295463938592920	0.0351664733065400
-0.536628801791570	-0.0546333136825200
-0.295463938592920	-0.0665099006248400
0.0285444717151500	0.297547906345710
0.0556648607799600	0.584015752240750
-0.0102300708193700	0.297547906345710
-0.0102009221870400	-0.0665099006248400
	-0.0546333136825200
	0.0351664733065400
	0.00843901203981000
	-0.0120141966670800
	-0.00135360470301000

It gives the wide range of selectivity of frequencies in higher and lower side of it. Hence it provides better lower bandwidth range with greater high preservation of frequencies. Value of Scaling and wavelet impulse response of proposed filter is given. In the program first image is transformed by the wavelet function into frequency domain where low and high frequency coefficients are converted and coded into a bit stream. This code is compared by the original images bit size and compression ratio is calculated. Then for reconstruction the bit stream output of encoder is decoded back to the frequency coefficients and then this is again converted back to the pixel matrix in the spatial domain by the same wavelet function in inverse transform.

• A.    Flow Chart

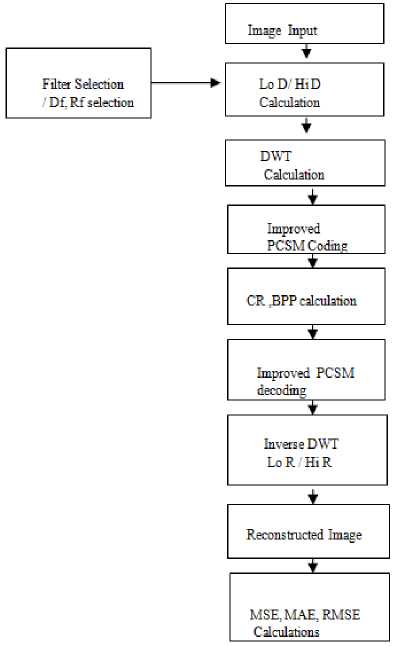
In this program first image is transformed by the wavelet function into frequency domain where low and high frequency coefficients are converted and coded into a bit stream. This code is compared by the original images bit size and compression ratio is calculated. Then for reconstruction the bit stream output of encoder is decoded back to the frequency coefficients. And then this is again converted back to the pixel matrix in the spatial domain by the same wavelet function in inverse transform.

• B.    Algorithm

Algorithm of the proposed work is divided into three parts and as follows:

/* start algorithm */

• Part 1 Filter Selection

Create a variable and assign it the image matrix

X= [input Image]

Select the filter type (as in the case of the existing filter) or choose the value of scaling and wavelet function (in the case of proposed filter).

Type= “Name of the Filter”

Calculate the low and high decomposition and reconstruction filter (Lo_D, Hi_D, Lo_R, Hi_R) respectively.

// Df(Scalling function), Rf(wavelet Function)

Df = (Value mentioned in table 1)=W

Rf = (Value mentioned in table 1)=W W = W/sum(W); // normalize filter sum. Lo_R = sqrt(2)*W; // Square Root

Hi_R = qmf(Lo_R); // Quadrature mirror filter QMF Hi_D = wrev(Hi_R);// reverses the vector Lo_D = wrev(Lo_R);// reverses the vector Part 2 Transformation

• L = 3 // Level of decomposition j = [h(:)' v(:)' d(:)' j];

  // details store

k = [size(x);k];

// size store

Out Put code IW = dwt(j,k)

// discrete wavelet Transform.

/*End of Algorithm*/

• Part 3 PCSM coding (formation of tree)

From the significant code {a b c d} in binary a three layer binary tree can be made to reduce the encoding length as follows:

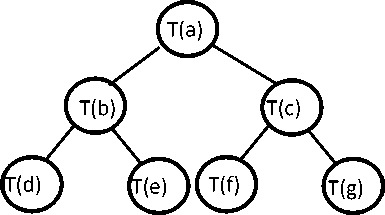
Fig.4. Binary Tree in Proposed coding formation of coefficients.

• V. Experiment simulation and result analysis

  In this paper, test image used for elegant the benefit of schemes used in improved PCSM coding with filter bank used. All the functions for the Improved PCSM code and proposed filter coding are written in the MATLAB 2011. In this program many inbuilt functions of MATLAB used for the development of different steps of the algorithm. Each phase presented a input image with respect to the functions. We have to obtain Discrete Wavelet Transform (DWT) of test images. In this implementation several predefined filters used along with the proposed filter.

• A.  Important Parameters For Measuring Performance

• i.  Execution Time

This is the time required to encode the original image with the help of image compression encoded algorithm. It is measured in second [10].

• ii.    Bit per pixel (bpp)

Bit per pixel also known as “bpp” of the image is defined as the number of bits of information stored per pixel of an image. Bit per pixel in the case of decoded image can be calculated by obtaining the total number of bits of the image i.e. number of significant coefficients multiplied by 8 and after this dividing them by total number of coefficients (or total number of pixels)[13].

• iii.    Mean Square Error (MSE)

Mean square error (MSE) is the cumulative squared error obtained between original and recovered image. Larger the value of MSE means the quality of image is poor [19].

• iv.    Compression Ratio

Compression Ratio is judge efficiency of the compression as the ratio of rate of the size or number of bits of the original image data to the size of the compressed image data [15].

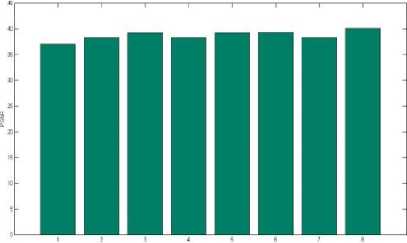
• v.    Peak signal to noise ratio (PSNR)

To judge how much information has been lost while the reconstruction of the same input digital image. A distortion measurement used for a lossy compression algorithm. The PSNR is commonly used to measure the performance of all lossy compression algorithms. PSNR gives the ratio between the power of corrupting noise and the high power of a signal and which affects the fidelity of its representation [16]. Other parameter like RMSE is the square root. Here, maximum possible pixel value of the image. It is 255 generally for unsigned 8-bit gray scale image. Small value of PSNR results in the poor quality image. But PSNR is very fast and easy to implement. For object detection requirement the Hardware requirement is a personal computer with 2 GB RAM and run for the MATLAN 11, 10 GB of Disk space is need and save the program and input output files. All the Results in this projected thesis work has been acquired on MATLAB2011, installed on Microsoft Windows 7 based operating system along with 2 GB DDR3 RAM, Intel Core i3, 2.20Ghz Processor and 320GB HDD.

• B.    Test Images Result

Fig.5. Test image

In this paper, test image example are used to elegant the benefit of schemes used in PCSM coding with filter bank. All the functions for the Improved PCSM code and proposed filter coding are written in the MATLAB 2011. In this program many inbuilt functions of MATLAB used for the development of different steps of the algorithm. Each phase presented a input image with respect to the functions. We have to obtain Discrete Wavelet Transform (DWT) of test images. In this implementation several predefined filters used along with the proposed filter. This test image is processed by the Improved PCSM code. In which Improved PCSM code is used without improved wavelet filter. All the parameters are calculated in this process. Then the existing wavelets filters are used to enhance the result of the PCSM code are all parameters are compared. Finally the test image is processed by the proposed filter with PCSM code to produce the best result in the wavelet compression technique. All the image compression parameters are compared and analyze, finally the improvement in the compression process is stated. In this paper we will analyze the all experimentation with this test images and its Results shows in the graphs and the tables. Following eight graphs are observed by the experimentation.

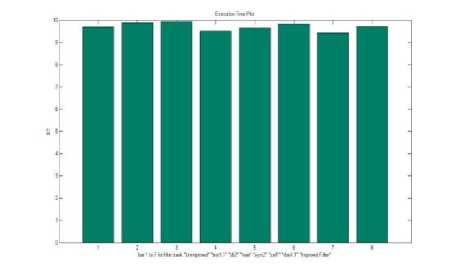
Fig.9. ET plot for Test image

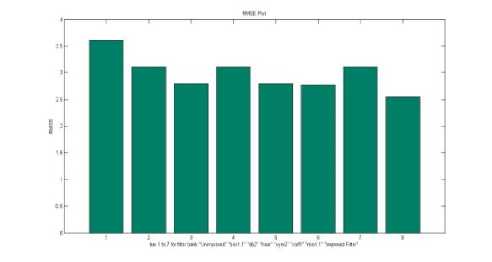
Fig.6. RMSE plot for Test image

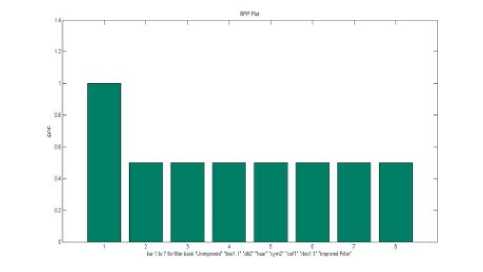
Fig.10. BPP plot for Test image

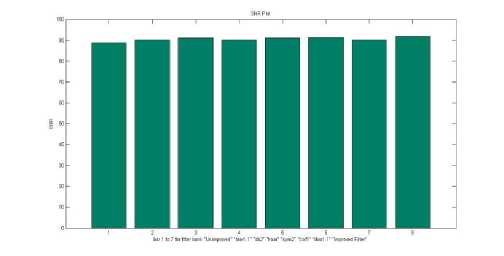
Fig.7. SNR plot for Test image

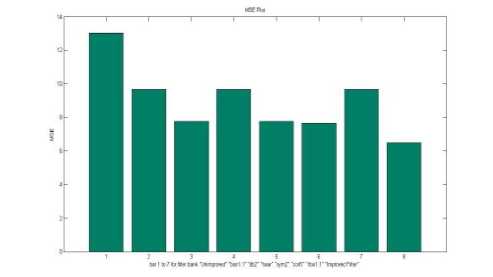
Fig.11. MSE plot for Test image

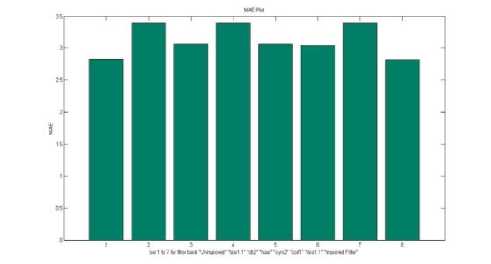
Fig.8. MAE plot for Test image

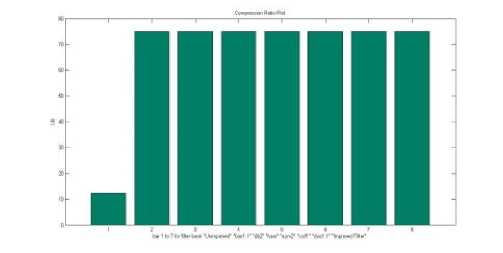
Fig.12. CR plot for Test image

PSHR B«

bat 1 to fl fee Пйеr bank 'Unmjrinrf* *Ьюг 1T ЧМ' ‘heat1 *1|т2‘ ‘cals* Myoi Г "irpmeii Fiiw*

Fig.13. PSNR plot for Test image

Fig.14.Reconstructed Image test

Table.2 Comparison Table of parameters

	PSNR	MSE	BPP	CR%	EX.TIME	MAE	SNR	RMSE
PCSM	36.9856	13.0173	1	12.5	9.8593	2.8255	88.8548	3.608
BIOR1.1	38.2825	9.6568	.5	75	9.2486	3.3895	90.1517	3.1075
DB2	39.2235	7.7756	.5	75	9.588	3.0609	91.0927	2.7885
HAAR	38.2825	9.6568	.5	75	9.3776	3.3895	90.1517	3.1075
SYM2	39.2235	7.7756	.5	75	9.4796	3.0609	91.0927	2.7885
COIF1	39.2908	7.6559	.5	75	9.5724	3.0428	91.16	2.7669
RBIO1.1	38.2825	9.6568	.5	75	9.3316	3.3895	90.1517	3.1075
IMPROVED FILTER	40.0028	6.4983	.5	75	9.6184	2.8162	91.872	2.5492

• VI. Conclusion

This work presents a computationally efficient method designed for image compression. The objective of this paper is to present PCSM Coding in a new scheme by which we can get a digital image which has not only a good quality but also a higher compression ratio. All the parameters are increasing when we are using the predefined filter in MATLAB instead of HAAR wavelet CR is increasing 75% of previous method with 3-5 % improvement in error and PSNR SNR parameters. This should be also noted that from the above obtained results for mean square error (MSE), power to signal noise ratio (PSNR), compression ratio (CR), execution time (ET) and bits per pixel (bpp). It concludes that all the coding methods provide different results for different images. Now in advancement of PCSM we are using the new filter to further increase the values. The improved and enhanced coding scheme provides further improvements in the MSE with 5 to 10% reduction reduced and in PSNR with the same amount of increment.

Future scope of the coding is to further develop a filter to enhance more the compression process and also we can change the value of the scaling and wavelet function in the coding part of the thesis to calibrate the improvement more. This method is also useful in the case of other image compression application like satellite imaging, medical imaging etc.