Image Compression and Reconstruction using Discrete Rajan Transform Based Spectral Sparsing

With the advancements in communication networks, one can witness an increase in the transmission of digital multimedia and images around the world [1-2]. In general, images are considered to have a large amount of information that is redundant and thus the transmission process can be improved by implementing compression techniques. The major benefit of compression is that it reduces the data storage requirements. It also offers an attractive approach to reduce the communication cost in transmitting high volumes of data over long-haul links via higher effective utilization of the available bandwidth in the data links. This considerably aids in reducing the cost of communication due to the data rate reduction. Because of the data rate reduction, data compression also increases the quality of multimedia presentations through limited-bandwidth communication channels [3]. Compression techniques help ease image and multimedia and similar such transmissions [4-8]. This has led to a reduction in the costs involved in storage in the past few decades. However, on the consideration of the large amount data storage and transmission requirements, the pace of development is still far from our expectations [9]. In order to achieve maximum information content with minimum storage requirements for various types of data, many novel techniques have been developed and proposed. There are basically two categories of compression techniques- lossless and lossy compression. Lossless compression, as the name implies, is the technique that involves no loss of data during the compression process and the pre-compressed signal can be restored. In contrary to the Lossless compression technique, Lossy compression technique involves loss of data [10]. Lossy compression algorithms are generally developed according to contrast sensitivity function of human visual system. Lossy techniques emphasize preservation of contrast only and thus provide higher compression ratio[11].Lossy compression usually involves having a trade-off between information loss and compression ratio. These lossy techniques are widely used in signal processing applications that involve digital images or audio. The Joint Photographic Experts Group (JPEG) standardized the concept of transforming image to the frequency domain in order to filter out noise components in an effort to achieve greater compression[9][12]. The speed of computation has always been considered as a weak link in the area of data compression. However, the currently evolving technology has forced onto focusing on limitations in storage capacity. The cost of memory involved in archiving documents or photographs or multimedia is high and this has influenced the zeal of researchers to develop efficient information reduction algorithms or techniques. As the technology in image processing systems, advances, such as greater resolutions and color definitions, the information stored in image files increases dramatically [13]. There have been many image compression coding techniques that have been developed based on transformation or decomposition algorithms and are also been put into practical use [9][14-17]. However, even though the algorithms that are based on transformation techniques can help achieve compression, complex calculation and processing time is a major drawback [18].

By using image coding techniques, one can achieve high compression ratio along with low distortion characteristics. As images are complex in nature, there is no existing transform in the literature that can optimally and efficiently represent the content in the image. For example, for an image which has an oscillatory texture, the performance of Fourier transform is better in terms of providing a sparse representation. Similarly, the Discrete Wavelet Transform (DWT) gives better performance if the image has isolated singular textures [19]. This fundamental concept led to a development of many algorithms. There are many algorithms which are standard and widely used in the field of image compression. The JPEG2000 standard is the most popular among these techniques and it is based on the basic fact that the images have a certain sparsity associated with them when they are represented by wavelets [19-22]. As an alternative to these traditional approaches, the use of Discrete Rajan Transform (DRT) for sparsification and image compression has been explored. This paper presents a comparison of DRT with widely used transforms- Discrete Cosine Transform (DCT) and DWT in terms of performance in image quality measurement parameters.

• II.    Related work

  The authors in [23] compared and made an analysis of image compression metrics using transform-based compression, especially the wavelet transform. They used different wavelets like Haar, Daubechies, Coiflet, Symlet and Biorthogonal wavelets etc on various grayscale and color images. Nineteen different wavelet transform basis functions were analyzed. In the case of color images, it was observed that Biorthogonal family wavelet Bior3.3 and Symlet family wavelet Sym6 produced better PSNR value of order 27.0686. It was concluded that each wavelet filter had a different performance for different fidelity metrics and different images and that the performance was related to the content in the image. Every time, for a different image, a proper wavelet function has to be the content of the image. Therefore it is appropriate to tailor chosen for achieving desired quality of reconstructed image.

DRT was previously used for sparsing speech data and compressing it in the spectral domain. It was applied to voice data and the resulting spectrum was sparsed by retaining its first component CPI (Cumulative Point Index) and forcing the other spectral components to zero. Thus, the spectrum was compressed to a maximum of 12.5% of the original data. As and when required the compressed spectrum could be synthesized using Inverse Discrete Rajan Transform and the reconstructed speech data analyzed for speaker recognition [24].

In this paper, DRT is used to sparse and compress the image data. DRT is applied to each 8-element block of the image and the resulting each 8-element spectrum is sparsed by retaining the first component (CPI-Cumulative Point Index) and a mid-spectral component. The other spectral coefficients are forced to zero. Then the compressed algorithm (Run-length encoding) is applied on the sparsed image to obtain compressed image. As and when required the compressed spectrum could be decompressed using run-length decoding and Inverse DRT.

• III.    Sparsification of Image using DRT

Rajan Transform (RT) is a variant of Hadamard Transform which was initially developed for the purpose of pattern recognition. RT has a homomorphic nature and it is permutation invariant. It is because of this property that RT has potential applications in pattern recognition algorithms like thinning, edge detection, contour detection, and detection of curves and lines in images and isolation of certain points in images [25-26]. Unlike RT, the generalized DRT has been moulded to exhibit isomorphism when the auxiliary phasor information associated with the spectrum is known apriori. The principle of DRT has been explained by the authors in [27].

With the help of DRT algorithm, both lossless and lossy sparse representation can be obtained. For several input signals, the transformed signal output obtained from DRT was observed. It was found that almost 23% of it was zero coefficients and many of the remaining coefficients were nearly zero. Thus, there is a possibility of achieving better sparse output by using DRT. However, there would have to be a trade-off between data recovery and the energy required for it. Hence, this transform was applied for images to exploit its sparsing nature. Different input grayscale images of dimension 512×512 have been considered. Each of the input images was divided into pixel blocks of size 8 and DRT was applied to it and the degree of sparsity associated with the transformed signal output has been calculated. Also, the scope of achieving the maximum possible sparsity has been analyzed by applying thresholding function, which, however, would result in loss of information in the signal. On the simulation of DRT on Lena image, out of the total 512×512 pixels, 9610 zero valued or (N-K) sparse pixels are obtained. The degree of sparsity obtained by considering just the output transformed signal of DRT is 3.7% or nearly 4%. Similarly for the ‘cameraman’ image,

103078 number of (N-K) sparse or zero valued coefficients were obtained. The degree of sparsity obtained for the cameraman image is 3.93% or nearly 4%. For the ‘pepper’ image also, a similar trend is observed. This is perfectly lossless and the original image can be recovered with infinite Peak Signal to Noise Ratio- PSNR (since no errors exist in this case). Depending upon the trade off that can be accepted by the end user, various levels of sparsity can be achieved. However, the sparsest representation possible using DRT is when only the CPI of each of the blocks is considered i.e. the information present in each of the pixels in each block is represented by only one pixel and thus the total image can be represented by only fewer numbers of pixels. In this case, for all the three images under consideration, the total number of zero coefficients possible is (512×512) – (64×64) i.e. 258048 and the maximum achievable degree of sparsity would be 98.44%. However, a considerable amount of information loss can be expected. To visualize the impact of the sparse representations, the image is reconstructed using Inverse DRT process. The PSNR (in decibels) for the lossy case mentioned above is found to be 20 and 24 respectively. There is always a scope to improve the PSNR or compress the signal by applying relevant algorithms. Application of DRT in perspective of sparse representation achievable has been focused on. Individual algorithms that help in improvising the PSNR and compressibility can always be employed. There is always a scope to improve the degree of sparsity of the signal obtained by considering only the Cumulative Point Index (CPI) values. However, the compromise would be the loss of information in the signal.

• IV.    Image Compression Using Drt

For the purpose of improving sparse representation, a special case of DRT can be used wherein the auxiliary phasor information in each stage is considered as 1. Considering the lossy case, even higher degree of sparsity can be obtained using (i) Cumulative Point Index (CPI, the first spectral component) values and (ii) CPI along with the mid-spectral component of DRT transformed output at different block lengths. But, in this case, a compromise has to be made to information loss in the signal [26]. DRT has potential applications in image processing and compression. In this paper, the application of DRT to obtain a sparse representation and compression of images is considered. Standard images have been considered and to make the DRT processing easier, the image has been divided into blocks of size 8. DRT is applied to it and the special case of DRT, as mentioned earlier, is considered.

The block diagram for image compression using sparsifying transform- DRT is shown in fig.1. The sequence of steps used in the algorithm for image compression using DRT is as given below:

• 1)    Input Image (W x W)

• 2)    Convert Image as a row of length W²

• 3)    Scan the Image in blocks each of length 8

• 4)  Apply DRT to the chosen vector and obtain the

DRT spectral sequence

• 5)  Preserve the Cumulative Point Index (CPI) value

and the mid spectral component value in the spectral sequence and force other elements to zero.

• 6)    Repeat the same process until the entire image is scanned and processed

• 7)   Resulting  sequence is the  sparsified  spectral

sequence

• 8)  Apply Run Length Encoding (RLE) and compute

the Compression Ratio

• 9)    Apply decryption algorithm to obtain the spectral sequence

• 10)    Apply Inverse DRT to reconstruct the image

• 11)    Calculate Mean-Squared Error (MSE), Peak Signal-to-Noise  Ratio (PSNR), Normalized Cross

Correlation (NCC), Average Difference (AD), Structural Content (SC), Maximum Difference (MD), and Normalized Absolute Error (NAE) for this reconstructed image with respect to the Original Image.

A similar algorithm is used for the case of DCT and DWT. The results thus obtained have been presented in the following section.

• V. Image Quality Measurement Parameters

In this section, a brief introduction to the quality measurement parameters used for the comparison of DRT with DCT and DWT has been discussed. It is a well-known fact that digital images can contain a variety of distortions while acquiring the image, or processing it or during compression and storage. Distortions may also be introduced during transmission and reconstruction process. In whatever way distortions occur, the outcome would be degradation in visual quality. In applications, wherein the image outcomes are to be analyzed or viewed by a human, subjective evaluation method is used. The drawback of this technique is that it is time-consuming, complex and expensive. However, in objective image quality assessment, quantitative measures are used to predict the image quality automatically. The classification in Objective image quality metrics is done based on the availability of original image which is free from any sort of distortions and comparison is made between the distorted and the original image. One such is the Full Reference approach, wherein the original or reference image is assumed to be known apriori. Practically, a reference image is not always available and a blind quality assessment approach is done. The commonly used and simplest full-reference quality metric is the MSE and PSNR. These involve simple calculations and they have a distinct physical meaning that makes logical sense. But they are not very well matched to perceive visual quality [28-37].

The seven quality measurement parameters used in this paper to assess the quality of the reconstructed image are given below:

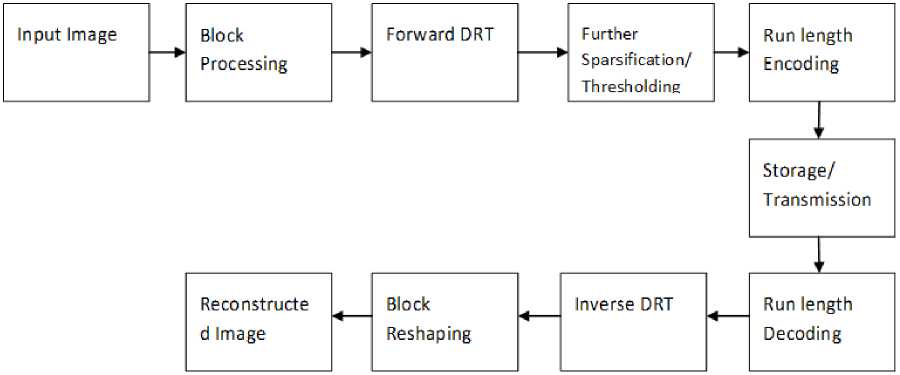
Fig.1. Block Diagram of Image Compression Using DRT

• A.    Mean-Squared Error (MSE):

Mean-squared error is the sum over all squared value differences divided by image size. For a two-dimensional image of size (M x N), MSE is given by the following equation

MN           ²

MSE = MN § § f I ⁽ x , ^y ) ^{- 1 (} x , ^{y ) ]}

Here I(x, y) is the original image and I'(x, y) is the reconstructed image. If the value of MSE is lower, it implies that there is less number of errors in the reconstructed signal.

• B.    The Peak signal to noise ratio (PSNR):

It gives a measure of the peak error in the reconstructed image. The equation of PSNR is given below:

PSNR = 10iog₁₀

' 255 2 '

_v MSE _v

It can be seen that there is an inverse relation between MSE and PSNR. Lower the MSE, higher is the PSNR. A higher value for PSNR is desirable as it literally means that the ratio of signal to noise is more.

• C.    Normalized Cross-Correlation (NCC):

It is a widely used metric that helps in evaluating the degree of similarity or dissimilarity between the original and reconstructed image. The value of NCC usually ranges between -1 to 1. The value 1 indicates that the alignment of the images is exact in the time series, however, the amplitude may vary [38-41]. The equation for NCC is given below:

MN gg I(x- y )• I (x, У )

NCC = ^=1 (3) MN     ²

gg [ I ( x , У ) ]

x = 1 y = 1

• D.    Average Difference (AD):

It is defined as follows:

Error = (Original Image – Reconstructed Image), AD = Error / (M*N).

In other words,

MN

AD = ZZ [ ^{1 ( x} , y ) ^- I ^{( x} , y ) ]     ⁽⁴⁾

MN x = 1 y = 1

• E.    Structural Content (SC):

Structural content identifies the degree of matching in the images. The more the regions common in both the original and reconstructed images, the more is the similarity between them [37]. The equation for SC is given below:

MN     ²

Ц[ I ( x , y ) ]

SC = -^=------

MN      ²

ZZ [ I <  x - y ) ]

x = 1 y = 1

• F.    Maximum Difference (MD):

It gives the variation of the method of paired comparisons [37].

MD = Max (| I ( x, y ) — I ( x, y )| )

• G.    Normalized Absolute Error (NAE):

This gives the numerical difference between the original and the reconstructed image [37].

NAE =

MN

ZZ| I(x, y) - I'(x, y)| x=1 y=1

MN

ZZ I ( x , y )

x = 1 y = 1

• VI.    Simulation Results

  For the purpose of simulation, different input grayscale images (Lena, Cameraman, and Peppers, etc...) of dimension 512×512 have been considered. Each of the input images was divided into 1×8-pixel blocks and DRT was applied to it and the degree of sparsity associated with the transformed signal output has been calculated. Also, the scope of achieving the maximum possible sparsity has been analyzed by applying thresholding function, which, however, would result in loss of information in the signal. On the simulation of DRT on Lena image, out of the total 512×512 pixels, 9610 zero valued or (N-K) sparse pixels are obtained. The degree of sparsity obtained by considering just the output transformed signal of DRT is 3.7% or nearly 4%. Similarly for the ‘cameraman’ image, 103078 number of (N-K) sparse or zero valued coefficients were obtained. The degree of sparsity obtained for the cameraman image is 3.93% or nearly 4%. For the ‘pepper’ image also, a similar trend is observed. This is perfectly lossless and the original image can be recovered with infinite PSNR (since no errors exist). Further sparse representation of the transformed signal can be obtained by applying thresholding function. After thresholding (threshold T=0) was considered for the Lena image, 134568 samples could be approximated to zero. The degree of sparsity that could be obtained is 51.3%. Similarly for the cameraman image, the number of samples that could be approximated to zero is 180273 and the degree of sparsity achieved is 68.7% and for the pepper image, the number of zero coefficients obtained is 131959; achieved degree of sparsity being nearly 51%. However, this would lead to loss of information in the image and thus can be classed as lossy. The transformed output from DRT was sparsified as mentioned above and RLE (Run Length Encoding) encryption technique was applied. This step was introduced so as to obtain more compression. To have a visual perception of the sparsity and the amount of information loss, the decryption algorithm was applied and reconstruction using IDRT has been done. For the purpose of comparison, DCT and DWT have been considered alongside DRT.

The simulation results were analyzed on the basis of seven quality measurement parameters – Mean-Squared Error (MSE), Peak Signal to Noise ratio (PSNR), Normalized Cross-Correlation (NCC), Average Difference (AD), Structural Content (SC), Maximum Difference (MD), and Normalized Absolute Error (NAE).

These seven parameters were analyzed for a set of 7 images and it was found that DRT gives better image quality in comparison with other candidate transforms. The observations for the seven different bench mark images have been tabulated in Table 1.

From the table 1, it can be noticed that the compression ratio obtained by using DRT for all the images is consistent and numerically higher compare to other candidate transforms considered in the experiment. Lower MSE can directly imply higher PSNR. It can be observed that the MSE for DRT is least compare to other transforms. Since the MSE for DRT is least, a high PSNR is observed. The NCC for DRT has the values closer to the ideal value of 1. Hence, it can be considered that the performance of DRT is better. The average difference in the coefficients obtained with DRT is least compare to the other transforms. Structural Content is closer to unity in case of DRT compare to other transforms. The metric of Maximum Difference in the coefficients is least for DRT compare to other transforms. The normalized absolute error is least for DRT compare to other transforms.

The simulation results illustrate that the proposed compression algorithm based on DRT is superior to the DCT and DWT both in the visual quality and all seven quality measurement parameters.

The reconstructed images with three different transforms are displayed in fig. 2.

• VII.    Conclusion

As an alternative to these traditional approaches, the use of Discrete Rajan Transform (DRT) for sparsification and image compression was explored. The Inverse Discrete Rajan transform (IDRT) can be used to retrieve the input image. DRT displays invariance to cyclic shifts, dyadic shifts graphical inverse of input signals. DRT has some limitations.

The performance of DRT is dependent on the correlation value of the data set i.e., if the samples in the input data are more correlated (eg. image), the performance of DRT is better. The performance of DRT is a linear function of the degree of correlation in input data.

Our results illustrate that we can achieve higher quality compression of images with DRT. We also observe that although RLE is lossless method and keeps the image quality well but it cannot be applied to all types of images as it lowers compression ratio to a certain extent.

For a slightly poor compression ratio, DRT yielded higher quality image than the other candidate transforms used.

Table 1. Simulation Results

		Mean Square Error	Peak Signal to Noise Ratio	Normalized CrossCorrelation	Average Difference	Structural Content	Maximum Difference	Normalized Absolute Error	Compression Ratio
Lena Image	DWT	1.3269e+04	6.9023	0.1267	193.3192	12.3267	255	0.8809	48.2468
	DCT	129.5269	27.0072	0.5073	100.2788	3.1080	227	0.5226	48.9304
	DRT	55.0869	30.7203	0.5079	100.1467	3.0904	227	0.5226	49.3568
Boat Image	DWT	1.4255e+04	6.5912	0.2499	97.3150	4.0021	255	0.7503	49.0181
	DCT	243.1366	24.2723	0.9876	0.0037	1.0122	151	0.0727	49.3683
	DRT	103.2301	27.9927	0.9954	-0.1242	1.0037	120	0.0467	49.6521
Zelda Image	DWT	7.4625e+03	9.4019	0.2503	68.3464	3.9950	185	0.7497	48.3963
	DCT	61.7036	30.2277	0.9939	0.0080	1.0061	108	0.0532	48.8831
	DRT	24.1837	34.2956	0.9987	-0.1246	1.0001	72	0.0333	49.5102
Baboon Image	DWT	1.3833e+04	6.7218	0.2510	96.7626	3.9839	230	0.7492	49.5232
	DCT	657.3608	19.9528	0.9687	0.0013	1.0278	161	0.1358	49.7063
	DRT	421.6507	21.8813	0.9780	-0.1249	1.0215	128	0.1074	49.7986
Cameraman Image	DWT	2.4370e+04	4.2623	0.2518	125.0226	3.9710	255	0.7489	48.0988
	DCT	503.7334	21.1088	0.9853	0.0066	1.0140	208	0.0645	48.9868
	DRT	266.3418	23.8764	0.9924	-0.1212	1.0070	159	0.0446	49.1974
Barbara Image	DWT	1.2563e+04	7.1399	0.2506	87.9941	3.9911	245	0.7496	48.7633
	DCT	348.1860	22.7127	0.9804	0.0049	1.0187	132	0.0973	49.2279
	DRT	183.6054	25.4919	0.9899	-0.1235	1.0093	103	0.0672	49.5750
Peppers Image	DWT	1.0642e+04	7.8607	0.2482	78.2574	4.0290	229	0.7510	48.7129
	DCT	184.9679	25.4598	0.9874	0.0045	1.0123	160	0.0691	49.2165
	DRT	82.4123	28.9709	0.9951	-0.1234	1.0040	115	0.0450	49.4339

While the DCT gives better compression ratio compared to DRT, image quality degrades because of the artifacts that result from the transform. Though the DWT provides better compression ratio compared to DCT and DRT but the image quality degrades with very poor PSNR. Thus DRT is superior to the DCT and DWT both in the visual quality and all seven quality measurement parameters.

Acknowledgment

(a)                 (b)                 (c)                 (d)

Fig.2. Simulation Results: Column (a): Original Images; Column (b): DWT Reconstructed Images; Column(c): DCT Reconstructed Images; Column (d): DRT Reconstructed Images