Image Encryption Using Chaotic Map and Block Chaining

Published Online July 2012 in MECS

With the extensive use of computer networks in our daily life, a frequent flow of digital images over transmission media has been in the rise. Most often, these images contain private or confidential information, or are associated with financial interests; this is why they have to be protected prior to their transmission to recipients. Consequently, techniques are necessitated to secure these images from leakage, as well as providing security functionalities like privacy, integrity, and authentication.

The whole idea of encrypting an image is to convert it to another one that is hard to understand [1], and to achieve that goal many techniques have been suggested. The simplest form of these schemes is to treat the image as textual data by converting the 2-D image array into 1-D data stream, and then any conventional cipher, such as DES or AES, can be applied [2]. However, the aforementioned method may not be well-suited in reality, especially under the scenario of on-line communication or in a classified image due to the intrinsic characteristics of an image such as bulk data and high redundancy, which complicate the operation and make it time consuming. An enhancement could be made to the previous method by utilizing the special nature of the human eye which can recognize partially distorted images. So, the image can be compressed before encryption [2].

Other schemes have been presented in order to fulfill the special characteristics of images. One of the widely used ciphers in this field is chaotic-based methods which present many desired cryptographic qualities since they provide a good combination of speed, high security, and reasonable computational overhead [3]. This is because of the distinct properties of chaos, such as quasi-randomness, dependence on system parameters, in addition to complex dynamics and deterministic behaviors [4]. Basically, a digital chaotic cipher can be stream or block, where in a stream cipher a chaotic system is used to generate a pseudo-random key stream that is used to mask plain texts [5], while in a block cipher plain text is divided into blocks and confusion is performed followed by a diffusion stage using a chaotic map and secret keys as the initial conditions [2].

Among all existing techniques, and whether they are chaos-based or not, one shared goal of these schemes is to dissipate the high correlation among the pixels of the image, since it is well-known that the strong correlation between pixels is a basic feature of an image, which makes the prediction of pixel’s value possible if values of neighboring pixels are known [6]. To address the problem of pixel correlation, three basic types of permutation can be applied to the plain image: position permutation, value permutation, and the combination form [7]. The difference between the first and the second processes is that the former scrambles the position of data, while the latter changes original values. If high level of security is required, the combination form can be used.

Many chaos-based cryptosystems for image encryption using 1-D, 2-D, or 3-D chaotic maps have been proposed. In [5], a chaotic key-based algorithm, CKBA, was introduced belonging to the category of value permutation. The scheme depends on generating a chaotic sequence using a logistic map. The grey level of each pixel is XORed or XNORed bit-by-bit with two secret keys ( key 1 or key 2 ) extracted from the chaotic sequence. The cryptanalysis of CKBA reveals that it cannot resist known/chosen plain-text attack, and only one pair of known/chosen plain image and cipher image is needed to reconstruct key 1 , key 2 , and then the binary sequence can be derived and the system is broken [8].

Later, an enhancement is added to CKBA to produce the so named Random Control Encryption Subsystem, RCES [7]. The two masking keys, key1and key2, become time-variant and are pseudo-randomly controlled by the binary sequence. The sequence specifies whether a simple permutation operation between adjacent pixels is required or not. Afterward, the plain-text is encrypted with XOR or XNOR operations using these keys. Although this scheme is much more complex than CKBA, it is still insecure against known/chosen-plaintext attacks [9].

The work described in [3] is another chaos-based cipher for image encryption with feedback. The algorithm is based on a logistic function with iterative cipher mechanism. The image is encrypted pixel by pixel; the value of the previously encrypted pixel is considered in each iteration. The system is robust against cryptanalysis attacks as a result of both the feedback and using an external secret key of 256 bits.

In our proposed scheme, we implement the encryption/decryption process using a logistic map and cipher block chaining (CBC), which provides high diffusion property, making the system highly secure against all types of attacks as has been proven in our results. We use a secret key of 80 bits, from which the parameters of the logistic chaotic map as well as the initial vector for the CBC are generated. The encryption/decryption process consists of keyed permutation of pixels and pixel value modification based on pseudo random sequences generated from a logistic chaotic map.

The rest of this paper is organized as follows. In section II, the security of RCES, as the base model for our work, is discussed. Our proposed scheme is then presented in section III. Experimental results and analysis are reported in section IV. Finally, the paper is concluded in section V.

• II.    Security of RCES

RCES is of the type of combination form cipher where position scrambling and value changing of pixels are used. Throughout this section, we talk in summary about the security of RCES and point out how it is vulnerable to different attacks. Details about RCES and how to break it can be found in [7, 9].

• A.    Known plain image attack

RCES is not secure against known plain image attack, because only one plain image/cipher image pair is needed to break it. The attack can be performed by obtaining the mask image, Im, by XORing the known plain image with the corresponding known cipher image. Once the mask image is obtained, all cipher images of the same or smaller size can be successfully decrypted by XORing the cipher image with the mask image pixel-by-pixel. If the pixel is not being swapped, it will be recovered correctly. Otherwise, the operation ends with wrong recovered value. In case of the plain image being partially swapped, the known plain image attack will effectively be able to recognize the image content or simply its shape. This is because RCES fails in dissipating the high correlation existing between adjacent pixels as the swapping process is done over these adjacent pixels themselves. Therefore, obtaining just half of the image under attack should be enough to get more details about the whole image.

Fig. 1 shows an example of this attack. The camera man image (256×256), Fig. 1(a), is encrypted using RCES to get the cipher image of Fig. 1(b). The mask image, Fig. 1(c), is calculated and used to decrypt the cipher image of Fig. 1(d) with the same size as the known plain image. The decrypted image is shown in Fig. 1(e) where most details are recovered correctly. Although some pixels are not recovered correctly, they can be recognized by the human eye due to tolerance of distortion.

We also investigated RCES behavior when a cipher image of greater size (compared to the mask-image) is attacked. Although the attacked cipher image (350×259) of Fig. 1(f) is of larger size, the mask image could be used to decrypt the first 256×256 pixels as shown in Fig. 1(g). This is considered a serious negative effect of the security of RCES.

When two or more plain/cipher image pairs are available, a swapping matrix ( S ) can be obtained by recording the swapped pixels, and the decrypted image will be more accurate [9].

• B.    Chosen plain image attack

Chosen plain image attack is performed in the same way as known plain image attack; however, in the former better decryption performance can be achieved.

• C.    Brute-force attack

In [7], it is claimed that the complexity of brute-force attack of RCES is O (2^{3 MN /2}). However, in [9], it is demonstrated that this complexity is vastly overestimated and it is proven that the actual number of possible keys for brute-force attack is only 2 ^k , where k < 48 secret bits.

• III.    The Proposed Scheme (CMBC)

In this section, we describe our CMBC image encryption as well as the decryption process. Before going in depth, we briefly describe the chaotic system and one of its simplest functions, the logistic map, as it is one base of RCES as well as our proposed scheme.

In mathematics, chaos theory describes the behavior of certain dynamic systems that may reveal extremely high sensitivity to initial conditions. This sensitivity causes the behavior of chaotic systems to be random. Such randomness occurs although chaotic systems are deterministic, meaning that their next dynamics are totally characterized by their initial conditions, with no random elements involved. This behavior is known as deterministic chaos, or simply chaos [10]. Chaotic systems have been widely used in the field of image encryption, as a result of the close relationship between chaos theory and cryptography [11]. A chaotic system mainly depends on logistic maps, where simple nonlinear dynamical equations are used to produce such chaotic behaviors. The relative simplicity of a logistic map makes it an excellent candidate to be used in chaos generation.

(a)

(c)                                          (d)

(g)

Figure 1. Cryptanalysis of RCES for different cipher images: (a) known camera man plain image, (b) its known cipher image, (c) its mask image, (d) cipher image under attack of the same size as (a), (e) decrypted image of (d), (f) cipher image under attack of larger size than (a), and (g) decrypted image of (f)

Mathematically, a logistic map is a polynomial mapping of degree 2 and has the form X i + 1 = p X i (1 - X i ), where i = 0, 1, ... is the iteration number, µ is a positive constant sometimes known as the biotic potential [12], and X 0 is the initial value which is a number between zero and one. A random sequence of values can be obtained by starting with random values of µ and X 0 , and running the logistic map a number of times that equals the required sequence length. The sensitivity to initial conditions is caused by the repeated folding and stretching of the space on which the map is defined. The value of µ controls the output of the logistic map and results in two cases: When д E [0, 3.57], no chaotic behavior is depicted, and the points concentrate on several values and could not be used for image cryptography. However, for д E ]3.57, 4], the logistic map exhibits chaotic behavior, and hence the property of sensitive dependence [13].

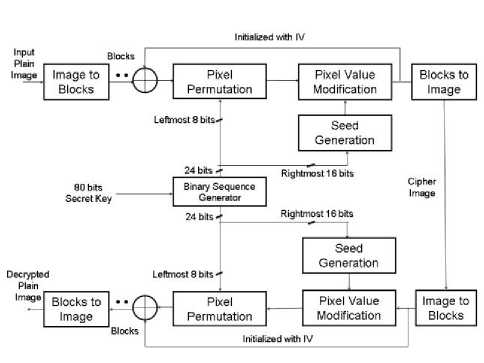
Figure 2. Block diagram of proposed scheme, CMBC

• A.    Binary sequence generator

The encryption/decryption process utilizes an external secret key of 80 bits length. The key has the form: K = k1k2…k20, where, each ki is a hexadecimal number. A chaotic logistic map Xi+1 = цXi (1-Xi) is used. For a highly chaotic property of the map, the value of X0 should be in the range (0, 1), and 3.9 ≤ µ < 4. In our algorithm, these two parameters are calculated using some mathematical manipulations on the secret key. To calculate the initial condition X0 and µ, the 20 nibbles of the secret key are used to calculate three intermediate values R1, R2, and S. R1 and R2 are computed using the first 12 nibbles of K, i.e., k1k2…k6, and k7k8……..k12 as follows:

R 1 = decimal( k 1 k 2 ……..k 6 ) / 2²³                (1)

R 2 = decimal( k 7 k 8 ……..k 12 ) / 2²³              (2)

The division by 2²³ is a normalization process. Further, the last 8 nibbles of the key are converted to decimal and used to calculate the intermediate value S :

i=20 k s = y »(3)

^ ¹⁾⁰

X0 = [S + R1] mod 1(4)

µ = 3.9 + [(S + R2) mod 1] / 10(5)

The mod operation is used to keep X 0 and µ within the chaotic behavior by extracting the fraction part of the result. Now, the logistic map is run to generate a chaotic sequence, { X i , i = 0 to ceil( M × N /16) – 1}. The leftmost 24 bits, b i , i = 0, 1, …, 23, of every X i are extracted.

• B.    Image to blocks

We divide the plain image/cipher image into ( M × N )/16 blocks each of 16 pixels, where M and N are the dimensions of the image.

• C.    Cipher block feedback

After converting the input plain image into blocks, each block of the plain image to be encrypted is XORed with the previous cipher-block, (or each block of the cipher image to be decrypted is XORed with the previous block coming out of the pixel permutation step). This kind of cipher block chaining (CBC) feedback adds more confusion and diffusion. However, we have to use a phony block called initialization vector, IV , for the first time of the encryption/decryption process where no cipher block is produced yet.

IV = Expand( k 5 k 6 k 11 k 12 )                    (6)

Here every bit of k i , i = 5, 6, 11, and 12, is expanded to 8 bits of the same value yielding 4 × 4 × 8 = 128 bits.

• D.    Pixel permutation

This step uses long distance permutation which decreases the correlation between adjacent pixels, in order to increase the security of our proposed scheme against statistical attack. Each one of the first 8 pixels of a block is decided to be permuted with its 8^th neighbor or not according to binary vector, b :

Swap b (16+ i ) ( P i , P i +8 ), i = 0 to 7, where b (16 + i ) is the (16 + i )^th bit of the 24 binary vector b of the current block, P i is the i ^th pixel in the current block, P i +8 is the ( i + 8)^th pixel of the current block, and the operation swap w ( g ( m ), g ( n )) is defined to swap g ( m ) and g ( n ) if w is equal to 1 or preserve their original positions if w is equal to 0.

• E.    Seed generation

For every block, two pseudo-random seeds, Seed 1 and Seed 2 , are generated from the corresponding 24 binary bits, b :

Seed 1 = У b i x 2^{7 4}                       (7)

i = 0

Seed 2 = У b 8 ₊ i -x 2 7 i                      (8)

i = 0

These equations calculate Seed 1 and Seed 2 by converting the first two bytes of b into decimal.

• F.    Pixel value modification

Each block is masked with the two pseudo-random seeds as follows:

For j = 0 to 15, do

Pj = Pj Ф FinalSeedj where

" Seed1  if  B (j) = 3, Seed1  if  B (j) = 2, FinalSeedj = j Seed2  if  B (j) = 1, Seed2  if  B (j) = 0, and B(j) is the decimal equivalent of the jth and jth+1 bits in the corresponding b binary vector.

• G.    Blocks to image

Here, constituting blocks are assembled into an image.

• IV.    Experimental Results

  Simulation of the proposed image encryption scheme was implemented using Matlab R2007b. Performance was measured on a 1.86 GHz PC with 512 Mbytes of RAM running Windows XP. We used ten images of different sizes with gray-scale (0-255). Two of these images, camera man (256×256) and peppers (512×512), are shown in Figs. 3(a) and 4(a), respectively. Their corresponding cipher images, using secret key value “456354689786544345DF”, are shown in Figs. 3(b), 4(b). Visual inspection of Figs. 3 and 4 reveals the effectiveness of the proposed encryption scheme in hiding the information contained in plain images. Obtained cipher images are decrypted to obtain the plain images shown in Figs. 3(c) and 4(c). In the following subsections, we discuss the security of the proposed approach.

• A.    Chosen/known plain image attack

We ran experiments to evaluate the performance of proposed model in comparison to RCES. Since the proposed model introduces cipher block chaining (CBC), it is expected that its security against chosen/known plain image attack is better than that of RCES. We have tested our scheme using the camera man image (256×256) and its cipher image to generate the mask image Im as shown in Fig. 5. The mask image has then been used to attack the cipher image of Lena (256×256), and the cipher image of trees (350×259); the results are shown in Fig. 5. It is clear that an intercepted cipher image cannot be recovered using a mask image as it was the case in RCES.

Figure 3. Encryption/decryption of camera man image: (a) plain image, (b) cipher image, and (c) decrypted image

(b)

(c)

Figure 4. Encryption/decryption of peppers image: (a) plain image, (b) cipher image, and (c) decrypted image

• B.    Key space analysis

For a secure image cryptosystem, the key space should be large enough to make the brute force attack infeasible. Our proposed method has 280 different combinations of the secret key compared to only 248 combinations used in RCES. An image cipher with such long key space is highly secure against brute-force attack and suitable for reliable practical use.

• C.    Statistical analysis

It is well known that many ciphers have been successfully analyzed with the help of statistical analysis and several statistical attacks have been devised on them. Therefore, an ideal cipher should be robust against any statistical attack. To prove the robustness of the proposed protocol, we have performed statistical analysis by calculating the histograms and the correlations of two adjacent pixels in the plain image/cipher image.

(b)

(f)

(g)

Figure 5. Results of chosen/known cipher image attack: (a) camera man plain image, (b) its cipher image, (c) mask image, I m , according to RCES, (d) Lena plain image, (e) Lena cracked image using the mask image of (c), (f) trees plain image, and (g) trees clacked image using the mask image of (c)

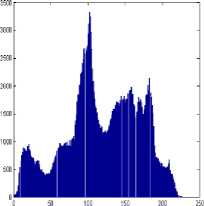
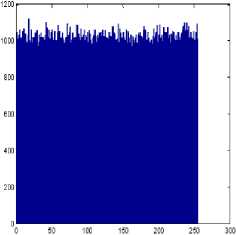
Histograms analysis

To prevent statistical attack, it is advantageous if the cipher image bears little or no statistical similarity to the plain image. An image histogram illustrates how pixels in an image are distributed by graphing the number of pixels at each intensity level. We have calculated and analyzed the histograms of several cipher images as well as their plain images. An example is shown in Fig. 6. The histogram of a plain image contains large spikes as shown in Fig. 6(a). These spikes correspond to intensity values that appear more often in the plain image. The histogram of the cipher image is shown in Fig. 6(b); it is clear that the histogram of the encrypted image is fairly uniform and significantly different from the histogram of the corresponding plain image and hence does not provide any clue to employ any statistical attack.

(a)

(b)

(c)

Figure 6. Histogram analysis of peppers image: (a) peppers plain image, (b) its histogram, (c) peppers cipher image, and (d) its histogram

(d)

Correlation coefficient analysis

We have also analyzed the correlation between two vertically adjacent pixels, and two horizontally adjacent pixels in plain and cipher images. The procedure described in [3] is used for this purpose. Correlation coefficient results for horizontal and vertical directions, applied to the tree plain and cipher images are shown in Table 1. The correlation distribution of two horizontally adjacent pixels in plain image/cipher image for the proposed protocol is shown in Fig. 7, where both horizontal and vertical axes represent the intensity of two adjacent pixels. It is clear from Table 1 and Fig. 7 that the correlation between adjacent pixel pairs is relatively high in the plain image – most of the points are located around the x = y straight line. In the cipher image, values are scattered throughout the plain indicating low correlation between pixels, which makes statistical attacks to the cipher image difficult.

Table 1. Correlation coefficients between adjacent pixels in (plain/cipher) of “trees” image

Direction of Adjacent pixels	Plain image	Cipher image
Horizontal	0.9738	0.0755
Vertical	0.9806	0.0768

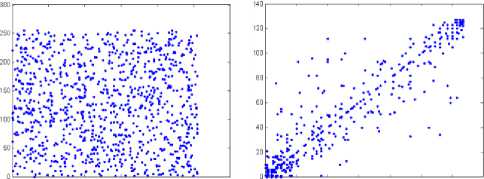
50       100       150       100       250       300                20      40      60      00      100      120     140

(a)                                       (b)

Figure 7. Correlation of two horizontally adjacent pixels: (a) for plain image, and (b) for its cipher image

• D.    Key sensitivity analysis

  High key sensitivity is required for secure image cryptosystems. For testing the key sensitivity of the proposed image encryption procedure, the plain image of Fig. 8(a) is encrypted using secret key K 1 = "456354689786544345DF" and the resultant cipher image is shown in Fig. 8(b). The same plain image is encrypted by making slight modification in the secret key, using K 2 = "456354689786544345DE" which differs

  from K 1 in the most significant bit, and using K 3 = "656354689786544345DF" which differs from K 1 in the least significant bit. Resultant cipher images are shown in Fig. 8(c, d). The three cipher images obtained using K 1 , K 2 , and K 3 are compared in pairs by calculating the correlation between the corresponding pixels. Table 2 displays computed correlation coefficients. It is clear from the table that no correlation exists among the three encrypted images even though these have been produced using slightly different secret keys.

Moreover, in Fig. 9, we have shown the results of some attempts to decrypt a cipher image with slightly different secret keys than the one used in encryption. Particularly, the plain image and corresponding cipher image produced using K1 are shown in Fig. 9(a, b), whereas the image of Fig. 9(c) is obtained by decrypting the cipher image of Fig. 9(b) using a slightly different key, K2. It is clear that decryption with a slightly different key completely fails and hence the proposed image encryption procedure is highly key sensitive.

• E.    Speed of CMBC

In this section, we introduce a comparison between the running times of CMBC and RCES. To improve the accuracy of our time measurements, each set of the timing tests was executed 10 times, and the average was computed. Table 3 summarizes encryption/decryption speeds for both schemes on images of different sizes. The results show that the run time of CMBC is slightly higher than that of RCES because of using cipher block chaining in the former as an additional step. However, the gain obtained is too much better security.

(c)

Figure 9. Decryption using slightly different secret keys: (a) plain image, (b) cipher image using K 1 , (c) decrypted plain image using K 2

Table 3: Speed Performance of RCES and CMBC

Image size in pixels	Encryption/decryption run time in seconds
	RCES	CMBC
256×256	2.801	2.821
350×259	3.858	3.902
512×512	6.044	6.113

(c)

(d)

Figure 8. Encryption using slightly different keys: (a) plain image, (b) cipher image using K ₁, (c) cipher image using K ₂, and (d) cipher image using K ₃

Table 2. Correlation coefficients between pixels of cipher images encrypted with slightly different keys

Image 1	Image 2	Correlation Coefficient
Cipher image obtained using K 1 Fig. 8(b)	Cipher image obtained using K 2 Fig. 8(c)	0.0604
Cipher image obtained using K 2 Fig. 8(c)	Cipher image obtained using K 3 Fig. 8(d)	0.0558
Cipher image obtained using K 3 Fig. 8(d)	Cipher image obtained using K 1 Fig. 8(b)	0.0637

• V.    Conclusion

The chaotic based approach has been proved to be a commendable alternative for the desire of having a simple and reliable image encryption scheme. Based on this concept, CMBC, a new cryptosystem for image encryption has been proposed in this paper. The new technique gains both the advantageous features of chaos and CBC chaining block cipher. The high level of efficiency and simplicity provided by the chaotic map together with the confusion and diffusion properties added to the system by involving CBC make the proposed scheme efficient and secure against most of the familiar attacks. Based on presented security analysis of CMBC, it is expected that our scheme will be secure and useful for real-time image encryption and transmission applications.

Acknowledgment

We thank anonymous referees for their constructive comments.