Image Recognition by Using the Progressive Wavelet Correlation

Images, drawings, photographs as means of communication among people, for sending and receiving messages have been part of everyday life for a long time. The easy to use World Wide Web, the reduced price of storage devices as well as the increased calculating power allow an essential and efficient management of large quantity of digital information. All of these factors offer a number of possibilities to the designers of real image-browsing and retrieval systems.

The earliest and the most sophisticated descriptorbased image recognition engine is IBM QBIC [1].

Another set of content-based tools for image recognition and retrieving have also improved throughout the years. Examples for such tools are VisualSEEk[2], WebSEEk [3] and ImageRover [4]. ImageRover uses low resolution for image representation in six regions in order to cover particular information along with the region based descriptors.

The present commercially available engines for image recognition, based on descriptors, provide no assurance that the required information from the libraries can be found. For some applications such as for example, collections of medical images or satellite images even the smallest details can be of great importance. Descriptor based retrieval engines cannot meet successfully such requirement.

An alternative approach to the problem set forth above is pixel (elements of digitalized image) based recognition and retrieval. This type of recognition involves analysis of the image, but this requires intense computing especially when the image contains many subtle details. Despite this fact, the existence of large number of operations per image does not seriously restrict the application of pixel-based recognition and retrieval techniques, especially when it comes to research and experimental purposes.

Pixel-based techniques work by locating a particular pattern in a given image library. Popular criteria for matching are the normalized correlation coefficients [5], which measure the differences between images and patterns from the library. The particular strength of these criteria is that they are insensitive to uniform differences in brightness.

Some of the works done in the area of PWC (Progressive Wavelet Correlation) [5] are outlined in Section II. Our proposal about applying of PWC for recognition images stored in a database is presented in Section III. Results of experiments are presented in Section IV.

In this section we summarize the technique described in [5], [6]. The fundamental operation for recognition is the circular correlation x ® y . The j ^th entry of the circular correlation is defined as:

N - 1

(x ® y)j = £ x+j mOd Nyi, j = 0,1, _, N - 1   (1)

i = 0

where x and y are column vectors of length N . The matrix form is x ® y = Xy , where X is left circulant matrix generated by x :

Fnx = (T»MRH ')(FmrHx )

where n = mr . The matrix F is an interlaced Fourier transform matrix with structure F_{m R} = Fm x I r , that is it has R interlaced copies of transform of size m . The matrix T is a Fourier update matrix ^that transforms F M , R into F_n : F_n = T N , M , r ^F m , R .

Fourier-Wavelet Multiresolution Theorem:

^F N I R , R ^H 1 x =

	x 0	x 1	•   xN - 1
X =	x 1	x	•    x 0 ♦           • • ♦
	L x N - 1	x 0	•   xN - 2 _

The notation ( P ^^

= ( ^T N / R , N I R 2 ,R ^X I R ^U 2,1 ^F N I R ², R ^{2 H} 2 x

FNx =

^T N , N / R , R ^H 1 ( ^Tn / R , N / R ², R ^X I R ^U 2,1 ^F N / R ², R ^{2 H} 2 x

denotes subsampling of P by

taking components whose indices are equal to i modulo R . Progressive wavelet correlation using Fourier methods is based on four theorems: the Wavelet-

Correlation Theorem, the Fourier-Wavelet Correlation Theorem, the Fourier-Wavelet Subband Theorem and the Fourier-Wavelet Multiresolution Theorem. To simplify the discussion all data are assumed to be onedimensional vectors.

Wavelet-Correlation Theorem:

where N = MR ². H 2 is a coarse transform matrix that is block diagonal with block of size R ² with the structure H^ = I_{N /r2} x ( W j x W j ) and operates on R ² subbands, each of length N / R ². W 1 is an R X R wavelet filter matrix with property W T W , = I_R . H 1 is a fine transform matrix that is block diagonal with block size NIR with structure H = I_{NJ R} X W_x . There is an update matrix U 2,1 that refines H 1 into H 2 , H 2 = U 2,1 H 1 . The matrix U 2,1 is block diagonal with block of size R ² with the following structure:

R - 1

(x ® y ^ R = Z((Hx)k 1R MHy)k 1R )

^k = 0                                     (3)

where H is wavelet-packet transform. X is the Kronecker product of I_M and W , H = I_м X W , where I_M is M X M identity matrix and W is an R X R matrix with property W^TW = I_R . The wavelet transform packet matrix H has a special structure. H is block diagonal with block size R . For instance, W can be 2 X 2 Haar matrix:

^U 2,1 = I N I R 2 X^{( W} 1 X I R )

W =

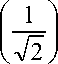
1

1

1

—

1

Fourier-Wavelet Correlation Theorem:

(x ® y L R =

JPEG compression [7] is based on the discrete-cosine transform (DCT) [5]. The matrix C 8 is an 8 X 8 DCT matrix that is used to create transforms of 8 X 8 subimages in a JPEG representation of an image.

The multiresolution recognition process relies on the factorization of the DCT matrix C 8 = V 8,4 V 4,2 V 2 , where V 2 and V 4,2 are matrices built from Kronecker products of W and the identity matrix.

The matrix V^ = I ₄ X W consists of 4 interlaced copies of W and is of size 8 X 8 . The matrix V 4,₂ has a structure V_{4 2} = I ₂ X ( W x I ₂ ) .

If we write C 8 = V 8,4 V 4,2 V 2 where V 8,4 is a matrix whose coefficients we want to compute, then

V 8,4 = C 8 V 2 - 1 V d                              (10)

obtain the last expression by multiplying both sides by V 2 ¹ V 4 2 - The matrix V 8,4 satisfies equation V ₄ =

(R -1                   7              Л

Z(Fm((Hx)k 1R »*(FM ((Hy)k 1R))

V k = 0                                      V

= Fm

where F is the Fourier transform matrix of dimension m and F is the complex conjugate of F .

Fourier-Wavelet Subband Theorem:

V ( w x I ₄ ). The inverse of V is given by (11), where / ( m ) = cos ( 2 n m /32 ) .

	Г 1	0	0	0	0	0	0	0     "
	0	Y ( 2 ) Y ( 7 )	0	Y ( 5 ) Y ( 6 )	0	Y ( 3 ) Y ( 6 )	0	Y ( 2 ) Y ( 1 )
	0	Y ( 6 ) Y ( 1 )	0	Y ( 3 ) Y ( 2 )	0	- Y ( 5 ) Y ( 2 )	0	- Y ( 6 ) y ( 7 )
- 1	0	0	0	0	1	0	0	0
V =	0	r ( 2 ) r ( 1 )	0	- Y ( 3 ) Y ( 6 )	0	/ ( 5 ) y ( 6 )	0	- Y ( 2 ) Y ( 7 )
	0	0	Y ( 6 )	0	0	0	Y ( 2 )	0
	0	0	Y ( 2 )	0	0	0	- Y ( 6 )	0
	. 0	- Y ( 6 ) / ( 7 )	0	Y ( 5 ) Y ( 2 )	0	Г ( 3 ) Y ( 2 )	0	- Y ( 6 ) Y ( 1 ) ,

The matrix H is an N x N matrix with the structure I_M x C ₈ where N = 8 M . It produces the JPEG transform of a vectors of length N . Let x be image stored as a JPEG transform of a vector Hx with an instance of a pattern y with JPEG transform Hy .

The algorithm consists of three incremental steps, each of them quadruples the number of correlation points. The process can be aborted at any stage if the intermediate results indicate that the correlation will not result in a match.

The three incremental steps are:

• 1.    Coarse correlation – Generate the Fourier transforms F Hx and F Hy . Multiply the transforms point by point and partition them into eight subbands of length M . Add these eights vectors and take the inverse Fourier transform of the sum. Every eighth point of the correlation is generated.

• 2.    m edium correlation – Multiply F Hx by T MM ,2 x 1 4 ) ( I m x ( ( W x 1 4 ) V ^-))        and

• 3.    Fine correlation – Multiply the x and y transform from the preceding step by ( T_{4M 2} mi x I ₂)

• 4.    Full correlation – Multiply the x and y transform from the last step by 1 _{8 M} , _{4 M} , ₂ ( I_m x V 2 ) and T m ,4 m ,2 ( I m x V 2 ) , respectively. Multiply the resulting vectors point by point and take the inverse Fourier transform of size 8 M to obtain the correlation at odd indices.

^{F ˆ} M ,8 ^Hy                               by

T 2 M ,M ,2 x 1 4 ) ( I m x⁽ W x I 4 V ¹ )) . Multiply the resulting vectors point by point and partition them in four subband of length 2 M . Add the subbands and you will create a single vector of length 2 M . Taking the inverse Fourier transform of size 2 M yields the correlation at indices that are multiples of 4 mod 8 of the full correlation.

(IM x V4,2 ) and (T4M,2M,2 x 12 )(IM x V4,2 ) , respectively. Multiply the resulting vectors point by point and partition them in two subbands of length 4M. Add the subbands and a single vector of length 4M will be created. Take the inverse Fourier transform of size 4M to obtain the correlation at indices that are multiples of 2 mod 8 and 6 mod 8 of the full correlation.

Figure. 1 is a flow diagram showing the steps performed for an image recognition according to the PWC method.

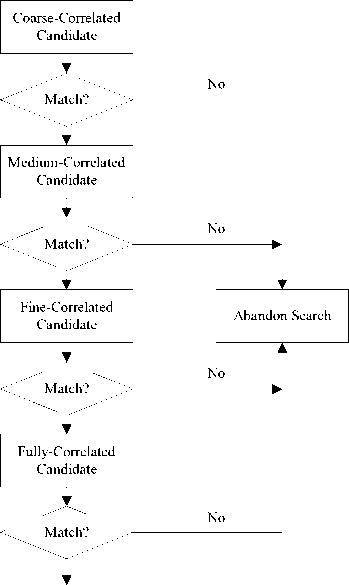
Image Found

Figure. 1 Flow diagram of PWC method

We investigate what happens in the two-dimensional case. Let the image size be N by N . In step 1, we have 64 subbands of length N ²/64. We perform one step of the inverse 2D JPEG transfer function, and one 2D step of the forward Fourier transform function. The next step includes adding the 64 subbands point by point to create a 2D array of size N /8 by N /8. Taking the inverse Fourier transform, we obtain the correlations at points that lie on a grid that is coarser than the original pixel grid by a factor of 8 in each dimension. In step 2, we obtain 16 subbands of size N ²/16 by adding the 16 subbands point by point, and taking the Fourier inverse. We will obtain the correlation values on a grid that is coarser than the original grid by a factor of 4 in each dimension. In step 3, we obtain 4 subbands of size N ²/4. Finally, in step 4, the full resolution is obtained.

Formulas for calculating normalized correlation coefficients that measure differences between images and patterns are given in [5]. Normalized correlation coefficients can be computed from the correlations described above. The normalization is very important because it allows for a threshold to be set. Such a threshold is independent of the images encoding.

The normalized correlation coefficient has a maximum absolute value of 1. Correlations that have absolute values above 0.9 are excellent, and almost always indicate a match found. Correlations of 0.7 are good matches. Correlations of 0.5 are usually fair or poor. Correlations of 0.3 or less are very poor. There is a tradeoff between the value of the threshold and the likelihood of finding a relevant match. Higher thresholds reduce the probability of finding something that is of interest, but they also reduce the probability of falsely matching something that is not of interest.

The progressive wavelet correlation provides guidelines how to locate an image in the image library. To make this method practical, we must first decide how to store the images. The initial choice is to store them in a disk file system which can be seen as the quickest and simplest approach.

A better alternative that should be considered is to store images in a database. Databases offer several benefits over traditional file system storage, including manageability, security, backup/recovery, extensibility, and flexibility.

We use the Oracle Database for investigation purposes. To store images into the database we use the BLOB datatype. After creation of one BLOB column defined table we also create a PL/SQL package with a procedure for loading images (named load). This procedure is used to store images into the database. The implementation of the progressive wavelet correlation in Matlab and the connection with the database are the next steps. The Database Toolbox is part of an extensive collection of toolboxes for use with Matlab.

Before the Database Toolbox is connected to a database, a data source must be set. A data source consists of data for the toolbox to access, and information about how to find the data, such as driver, directory, server, or network names. Instructions for setting up a data source depend on the type of database driver, ODBC or JDBC.

For Windows platforms, the Database Toolbox supports Open Database Connectivity (ODBC) drivers as well as Java Database Connectivity (JDBC) drivers. For UNIX platforms, the Database Toolbox supports Java Database Connectivity (JDBC) drivers. An ODBC driver is a standard Windows interface that enables communication between database management systems and SQL-based applications. A JDBC driver is a standard interface that enables communication between Java-based applications and database management systems. The Database Toolbox is a Java-based application. To connect the Database Toolbox to a database’s ODBC driver, the toolbox uses a JDBC/ODBC bridge, which is supplied and automatically installed as part of the MATLAB JVM. Figure. 2 illustrates the use of drivers with the Database Toolbox.

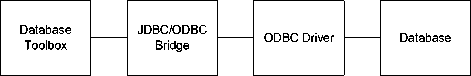
Windows platform

Unix and Windows platform

Figure. 2 The use of drivers with the Database Toolbox

If the Windows-based database supports both ODBC and JDBC drivers, the JDBC drivers might provide better performance when accessing the database because the ODBC/JDBC bridge is not used.

The connection definition can be established using either the Oracle ODBC driver or the Microsoft ODBC driver for Oracle. To use these drivers, it is necessary to have Matlab and the Oracle client installed on the same computer. During testing we realized that Microsoft ODBC drivers for Oracle cannot be used for tables with columns of data type LOB. For testing purposes JDBC drivers were usually used.

The last step in the adaptation is to create Matlab applications that use the capabilities of the World Wide Web to send data to Matlab for computation and to display the results in a Web browser. The Matlab Web Server depends on TCP/IP networking for transmission of data between the client system and Matlab.

In the simplest configuration, a Web browser runs on your client workstation, while Matlab, the Matlab Web Server (matlabserver), and the Web server daemon (httpd) run on another machine as shown in Figure. 3.

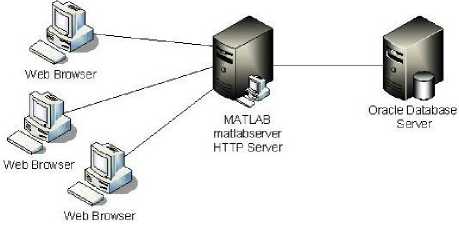
Figure. 3 The simplest configuration

In a more complex network, the Web server daemon can run on a separate machine (Figure. 4).

The input mask of our application consists of three parameters: the image size N, the threshold thr, and the name of the image that we are looking for (Figure. 5).

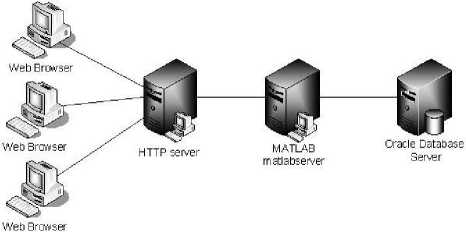
Figure. 4 HTTP Server running on separate machine

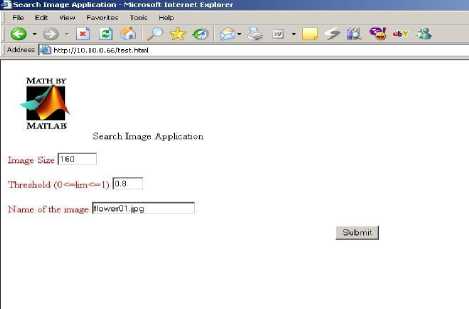
Figure. 5 Input mask of our application

• IV.    Experimental results

This section represents experimental results obtained by means of image retrieval through an algorithm of progressive wavelet correlation.

Different experiments were set up as follows:

• •    The required image is included several times in the database with different names;

• •    The image is included only once in the database;

• •    Aside from the required image, the database also contains an image very similar to the required one (smudged in some parts or an image generally slightly different);

• •    The required image is not present in the database.

Oracle 10g version 10.1.0.2.0, served as our database, while we used Matlab version is 7.0.4.365 (R14) Service Pack 2 for image recognition.

(c)                               (d)

(e)

Evaluation of the quality of the system concerning its precision p is estimated using the following the definition:

| A(q) ∩R(q) | | A(q) |

where q stands for query, R ( q ) signifies a set of relevant images for the query in the database, while A ( q ) stands for the set of images returned as a response to the set query q .

In the following tables are given precision for different correlation threshold values ranging from 0,2 to 0,7 with step 0,1. The number of images in the database is 1000.

(a)                                 (b)

Threshold	0,2	0,3	0,4	0,5	0,6	0,7 - 1
Retrieved images	911	640	285	79	18	6
Precision	0,007	0,009	0,02	0,08	0,33	1

Threshold	0,2	0,3	0,4	0,5	0,6	0,7 - 1
Retrieved images	761	435	113	19	8	8
Precision	0,01	0,02	0,07	0,42	1	1

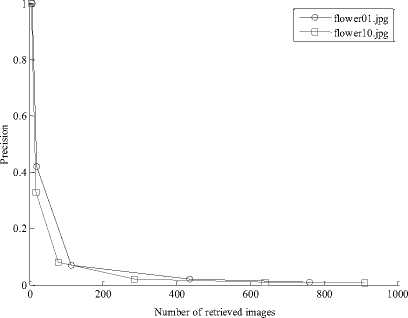
Considering the Tables 1 and 2 and Figure. 7 , it can be concluded that a high accuracy value can be obtained for correlation threshold values greater than or equal to 0,7.

Figure.9 Two very similar images

400            600

800    900

Number of retrieved images

Number of retrieved images

Threshold	0,3	0,4	0,5	0,6	0,7	0,8 - 1
Retrieved images	719	412	119	14	2	0

For correlation threshold values greater than or equal to 0,8 there are no images retrieved from the database. Therefore, if the correlation threshold is set sufficiently high, the system correctly predicts the absence of the image.

• V.    Conculsion

The main feature of PWC is its high accuracy. With the choice of an adequate correlation threshold it is possible to conclude which case it comes, from four possible cases:

• •    the given image is present in the database;

• •    there are images similar to the required one with different names;

• •    there are images slightly different from the required one;

• •    the required image is actually included in the database.

The studied examples indicates that with the selection of a threshold value greater than or equal to 0,7 provides that the required image is included in the database. Such selection of threshold gives the accurate number of images identical to the required one comprised in the database. With a correlation threshold greater than or equal to 0,9 a slight difference between two very similar images can be ascertained. In our examples, when the minimal threshold value is 0,8 it is established that the required image is not included in the database.

Due to the large number of operations, the pixelbased methods for image recognition and retrieval are slow compared to commercially available content-based systems. We believe that in the coming years PWC based methods will be able to achieve detailed analysis of thousands of images per second.

Also of future explorations focused on the construction of systems for identifying and extracting files, no matter which technique uses the system, expected response to the question of assessing the quality of the system in terms of efficiency and applicability [8,  9]. Retrieval systems should be comparable for the purpose of identifying the good techniques.

• [1]    M. Flickner, H. Sawhney, W. Niblack, et al, “Query by image and video content: The QBIC system,” IEEE Comp. , vol. 28, pp. 23-32, Sept. 1995.

• [2]    J. R. Smith and S. F. Chang, “Querying by color regions using the VisualSEEk content-based visual query system” Intelligent Multimedia Information Retrieval (Maybury, MT, ed). AAAI Press, Menlo Park, CA, 23-41, 1997a.

• [3]    J. R. Smith and S. F. Chang, “An image and video search engine for the World-Wide Web” in Storage

  and Retrieval for Image and Video Databases V (Sethi, I K and Jain, R C, eds), Proc SPIE 3022, 8495, 1997b.

• [4]    S. Sclaroff, L. Taycher, and M. La Cascia, “Imagerover: A content-based image browser for the world wide web,” IEEE Wksp. Content-Based Access of Image and Video Libraries , pp. 2–9, June 1997.

• [5]    H. S. Stone, “Progressive Wavelet Correlation Using Fourier Methods,” IEEE Trans Signal Processing , vol. 47, pp. 97-107, Jan. 1999.

• [6]    H. S. Stone, “Image Libraries and the Internet,” IEEE Commun. Magazine , pp. 99-106, Jan. 1999.

• [7]    G. K. Wallace, “The JPEG still-picture compression standard”, Commun. ACM, vol. 34, no.4, pp. 30-44, Apr. 1991.

• [8]    Sagarmay Deb , Multimedia Systems and ContentBased Image Retrieval , , University of Southern Queensland, Australia, 2004.

• [9]    Ritendra Datta, Dhiraj Joshi, Jia Li and James Z. Wang, “Image Retrieval: Ideas, Influences, and Trends of the New Age,” ACM Computing Surveys, vol. 40, no. 2, article 5, pp. 5:1-60, April 2008.

Igor Stojanovic is a Assistant Professor at the Faculty of Computer Science in the ‘Goce Delcev’ University – Stip, Macedonia. His research interests are multimedia, image retrieval, image recognition, digital video and image processing.

Aleksandra Mileva is a Assistant Professor at the Faculty of Computer Science in the ‘Goce Delcev’ University – Stip, Macedonia. Her research interests include multimedia, cryptography, quasygroups, network security..

Dragana Stojanovic is on postgraduate study on the Faculty of Medical Science in the ‘Goce Delcev’ University – Stip, Macedonia. Her research interest is improving the process of diagnosis by means of image processing.

Ivan Kraljevski is on post doctoral study at Institute of Acoustics and Speech Communication, Faculty of Electrical Engineering and Information Technology, TU Dresden, Dresden, Germany. His research interests are multimedia, audio, video and image processing.